基于EM算法的知情交易概率估计
尹 康(湖北经济学院 经济与环境资源学院,湖北 武汉 430205)
一、引 言
知情交易作为金融市场微观结构领域的一个重要概念,受到理论研究者和市场从业人员的高度关注。知情交易是市场中持有内部信息的投资者所发起的交易,它反映了市场中信息不对称程度,同时知情交易的出现也会对市场运行质量产生持续而又深远的影响,因此准确度量市场中知情交易水平是进一步讨论其他问题的基础。Easley等以序贯交易模型(EKOP模型)为基础,提出知情交易概率(Probability of Informed Trading,PIN)这一指标来度量市场交易活动中基于私有信息交易的比例[1]。由于该指标具有较好的理论背景且便于解释,故一经提出便得到大家广泛认可。20年来,已有大量文献利用PIN指标来描述世界各国或地区的证券市场中知情交易水平。目前,PIN指标已被广泛用于公司金融、投资、资产定价以及市场微观结构等领域。
在国内,有不少学者利用EKOP模型所构建的PIN指标,对中国证券市场的知情交易水平进行了度量。国内一些学者根据Easley等的估计思路,对中国上市公司不同时段、不同样本集合股票的知情交易概率(PIN)进行过估算,这些估计结果被用于分析中国证券市场的信息风险、价格波动、市场定价以及上市公司财务审计等各方面[2-5]。
然而,许多学者在使用PIN指标过程中,发现传统的PIN估计方法存在系统性偏误。Brockman等用EKOP模型估计了香港证券市场532家公司的PIN,其中有11家公司因为参数不收敛或是角点解的原因无法给出合理的PIN估计[6]。Brown等以美国三大证券市场共5 754家公司34 035组季度观测数据为样本,因为在参数估计过程中出现数值溢出,致使其中5 393组季度数据无法估计出PIN[7]。Easley等用2001年2 037支股票的年度数据估计PIN,其中有47支股票因为数据溢出未能给出合理估计,这些未给出PIN估计的股票,其市值占市场总市值的23.7%[8]。正如Ersan等所做的总结,传统的PIN估算方法在成交比较活跃的市场面临三个计算方面的障碍:一是交易活跃导致买卖单数量较大,使得极大似然估计容易出现数值溢出;二是估计结果频繁出现边界解;三是估计结果对初始值设定极为敏感[9]。
为了解决传统估计方法可能存在的估计偏误,Easley等尝试利用工具变量以及Vega利用自助法(Bootstrap)来控制PIN估计过程中存在的偏误,从实践效果看,这些方法效果不太理想[10-11]。Easley等相继提出通过对似然函数因子化来克服优化过程中出现数值溢出,从而降低或消除PIN的估计偏误[8,12]。Jackson建议对每天的买卖单数据同比例缩小一定倍数来克服似然函数优化过程中出现数值溢出[13]。但是,从泊松分布的特征可知,这种做法可能导致估计结果出现更大的扭曲。Gan等认为在已有的这些改进措施中,似然函数因子化是相对可行的一类改进方法,而LK因子化又表现得比EHO因子化方法要好[14]。然而在本文接下来的研究中可以发现,似然函数因子化的做法虽然对纠正PIN估计偏误有一定效果,但仍存在改善空间。
本文在前述研究工作的基础上,提出利用EM算法的思路重新设计EKOP模型中似然函数的估计方法,并且根据EKOP模型的理论特征设定待估参数的初始值。最后,以模拟数据和市场交易数据为基础,分别给出了EM算法、EHO因子化以及LK因子化的估计结果,并从数值溢出和估算效率两方面对这三类估计进行评价。
二、传统的知情交易概率度量
(一)EKOP模型
当投资者根据其所持有的私有信息进行交易时,信息不对称就会在市场上自我呈现。虽然我们无法判断具体某一笔交易是否为知情交易,但是可以从市场中买卖单的不平衡状况推断知情交易者的存在,这种可观测性给Easley等提出的EKOP模型提供了一种理论上的直觉解释。在EKOP模型中,做市商通过对订单流的学习来推断交易者的类型,随着知情交易者的参与,在交易日结束时,市场交易价格最终将收敛到私有信息完全揭示时的资产真实价值。通过对一段时期内每个交易日订单流的观测,可以利用EKOP模型所提供的框架对市场中知情交易概率进行估计。
EKOP模型从理论上看与Glosten等所提出的序贯交易模型一脉相承[15]。在一个序贯交易模型中,潜在的买者和卖者与做市商进行交易,市场中可供交易的风险资产只有一种。做市商的风险偏好是风险中性的,定价策略则是竞争性的,其主要职能是制定交易的买、卖价格,接受并处理市场交易者提交的订单。在模型中,假设交易者以某种特定概率结构相互独立地到达市场,在给定市场买卖价格面前,交易者可以选择交易或者不交易;做市商从这些陆续到达市场的订单中提炼出相关市场信息从而更新他们的市场定价。

市场中的交易者分为知情交易者和非知情交易者两类。知情交易者是风险中性的,同时也是一个价格接受者。后一个特征表明知情交易者不会采取任何策略性交易行为,而只是遵循简单的利益最大化的原则进行交易,即如果市场有利好消息发生,则买入;如果利空消息,则卖出。知情交易者并不考虑其买卖行为对价格的影响,更不会把这种影响纳入其交易决策。非知情交易者的交易行为要复杂一些,如果非知情交易者是基于投机的原因而进入市场交易的话,那么在市场中存在知情交易这一事实面前,他们最好的选择是离开市场。为了避免市场中出现这种无交易均衡,假定非知情交易者并非出于投机原因而是流动性需求进场交易。因此,有些文献也把这类交易者称为噪音交易者或流动性交易者。同时,我们认为非知情交易者的买卖方向应是随机的,他们买或卖的概率各为0.5。
做市商的竞争性定价原则意味着,买卖价格的确定要求做市商基于以往交易信息的期望利润为零,但做市商在与知情交易者交易时会遭受损失,这迫使做市商必须到非知情交易者那里得到补偿,而适时调整买卖价差便是实现这种补偿的有效机制。

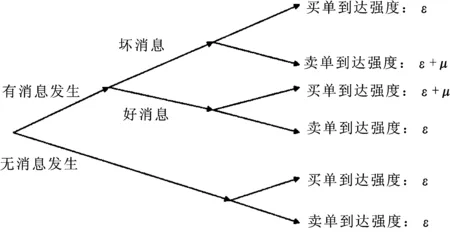
图1 序贯交易树形图
根据上述序贯交易结构,在给定时间内,总委托单的期望值为αμ+2ε,知情委托的期望值为αμ。因此,对于给定的一笔交易,其为知情交易的概率为:
(1)
(二)PIN的估计
Easley等基于某支股票各交易日的买卖单数据,构造了一个包含参数{α,δ,ε,μ}的似然函数[1]。通过对似然函数的优化给出参数的估计值,从而计算出给定股票的知情交易概率。假定在第i个交易日,i∈[1,2,…,I],对某支股票共观测到Bi笔买单和Si笔卖单,由前面的交易结构可知,如果第i天没有消息发生,则似然函数为:
(2)
如果第i天有坏消息发生,则似然函数为:
(3)
如果第i天有好消息发生,则对应的似然函数为:
(4)
对任意一个交易日,无消息、坏消息以及好消息发生的概率分别为:1-α、α(1-δ)、αδ,因此对于第i天的似然函数为:
L(α,δ,μ,ε|Bi,Si)
=(1-α)f1(Bi,Si)+αδf2(Bi,Si)+
α(1-δ)f3(Bi,Si)
(5)

(6)
通过最大化式(6),可以求解出参数{α,δ,μ,ε}的估计值,但是这一求解过程可能会遇到一些障碍。首先,要注意的问题是参数的取值范围约束,α、δ为概率参数,取值应在(0,1)之间;μ、ε作为泊松流的强度,取值均应大于0。其次,Bi、Si作为一个交易日内的买卖单笔数,在式(6)中,有Bi、Si的指数函数以及阶乘运算,当Bi、Si的取值较大时,似然函数的计算结果可能会超出软件所许可的数值范围,这种数值溢出也称为浮点运算溢出(the Floating-Point Exception,FPE),它将会影响到软件的优化求解,所得到的参数估计值可能会有偏误,严重时无法给出参数估计。
从最优化算法可知,有约束优化相比无约束优化在算法设计上要复杂许多。鉴于此,Easley等对参数的取值范围约束提出一个折中解决方案,建议对参数进行变换,对α、δ做Logit变换,即令:
(7)
δ类似;μ、ε做指数变换,即μ=exp(μ*),ε=exp (ε*)[1,10]。将新参数α*、δ*、μ*、ε*代入似然函数式(6),虽然求解过程变成无约束优化,但同时也使得目标函数的表达式变得更为复杂。
对似然函数式(6)的最大化,无法给出参数的显示解,只能通过数值优化的方法获得一个数值解。为了避免直接对似然函数优化所带来的数值溢出问题, Easley等通过对似然函数进行因子化处理以便更有效地进行数值优化[8]。对数似然函数的因子化变形结果如下:
L(B,S|θ)


(8)

L(B,S|θ)

αδexp (e2i-emax,i)+(1-α)exp (e3i-emax,i)]
(9)

对式(8)和(9)的优化求解,一般利用Quasi-Newton方法,但该方法对初始值的设定较为敏感,给定一组初始值,求解出的结果可能是全局最优也可能是局部最优,不恰当的初始值还有可能出现边界解。
三、基于EM算法的改进
在对似然函数的优化方法上,Easley等使用二次爬山法(Quadratic Hill-climbing)求解参数,Brockman等利用统计软件(SAS、STATA)中自带的程序求解参数,其基本原理都是Quasi-Newton算法[1,6-7,12,16]。考虑到EKOP模型中的似然函数由混合泊松分布构成,运算结构上先求和再求积,这种混合泊松分布的概率密度函数如果直接做数值优化,显然是缺乏效率的。如果需要计算的股票较多而且数据量较大时,这可能是一个严重的问题。在对这类目标函数进行优化时,EM算法相比以往的直接优化方法,在估计结果的合理性以及计算速度上都更有优势。下面简要描述用EM算法优化参数求解过程。
引入不可观测的示性变量Zi=(Zi1,Zi2,Zi3),Zi的取值遵循下列原则:
(10)
对应的概率分布:
(11)
新的似然函数:
(12)
对数化的似然函数:

(13)
最大化的一阶条件:
(14)
由式(14)中第一个等式可得:
(15)
由式(14)中第二个等式可得:
(16)
联合式(15)、(16)解得:
(17)
(18)
对于各类消息发生的概率:
上述结果即为EM算法中M步的结论,接下来求解E步:zik未知,考虑用E(zik|Bi,Si)代替。显然有:
(19)
因此,EM算法的迭代程序为给定参数初始值后,E步的迭代结果:
(20)
式(20)经展开化简,又可以表示为:
γ(m+1)(zi1)=
(21)
γ(m+1)(zi2)=
(22)
γ(m+1)(zi3)=
(23)
然后给出M步的迭代结果:
(24)
(25)
(26)

(27)

四、初始值的设定
Yan等以纽交所MNR股票为例,用80组不同的初始值对式(8)、(9)分别进行优化,结果发现,在两个模型中各有34组初始值的优化解为边界解,其中22组初始值求解出α=0,12组初始值求解出α=1[16]。α取0或1的结果显然不符合市场运行的实际情况。为了有效地设置初始值,避免求解出的参数值缺乏现实意义,Yan等提出利用矩条件来设定初始值的方法。在该方法中,α、δ的取值范围为[0,1],因此初始值的设定在[0,1]之间等距选择,如(0.1,0.3,0.5,0.7,0.9),μ和ε的取值范围为(0,+),利用与μ、ε两个参数有关的矩条件来限定其初始值的取值范围,矩条件如下:
E(B)=α(1-δ)μ+εorE(S)=αδμ+ε
(28)
这两个矩条件在设定中只能利用一个,因此对样本信息利用不够充分。本文考虑使用下列矩条件:
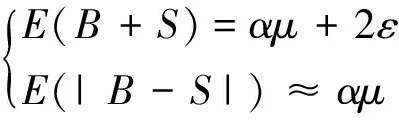
(29)
(30)
其中αi、δj∈{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9},所有参数的初始值在理论上是合理,避免Yan等文中因初始值不符合理论设定所进行的二次剔除,因此在设定上更为有效。
五、模拟结果的比较
为了比较Easley等所提出的估计方法与本文所提出的EM算法在PIN估计上的差异,考虑模拟产生三组买卖单数据,在这三组数据中交易天数都被假定为200天,买卖单的提交满足EKOP模型的基本设定[8,12]。在数据A中,假定消息发生概率α=0.1,利空消息发生的概率δ=0.3,知情交易订单的提交强度μ=100,非知情交易者的买卖单提交强度均为ε=40;在数据B中,α和δ的设定不变,μ=5 000,ε=2 000;在数据C中,α和δ的设定不变,μ=100 000,ε=40 000。在估计EHO模型和LK模型中,似然函数的优化使用R软件中optim()函数,优化方式选择BSFG算法。三种参数估计方法的初始值均按照式(30)中设定,估计结果汇总参见表1。

表1 基于模拟数据的优化结果比较
模拟生成的三组数据的数量级依次增加,数据A的数量级以百计,数据B以千计,数据C以万计。从表1可以看出,在这三组数据中,EHO方法仅能对第一组数据给出估计;在后两组数据中,无论初始值如何选取,该方法都因为数值溢出而无法给出最终估计结果;LK方法在第一组数据中表现良好,能给出有效估计,在第二组和第三组数据中,估计结果开始对初始值的设定变得敏感;在数据B中,有7组初始值无法给出估计,其余74组有效估计中,仅有一组初始值对应的估计结果达到最优;在数据C中,有14组初始值无法给出估计,余下67组初始值所对应的估计结果各不相同,无一达到最优。EM方法在三组数据中表现非常稳定,在每一组数据中,无论初始值如何调整,估计结果都能达到最优。从模拟结果来看,EM估算方法在估计EKOP模型的参数上比现有的方法更为稳健,在处理大额买卖单数据不易因数值溢出而导致无法估计参数。另外,根据表2的结果可以发现,在处理数据A时,EHO方法对81组参数初始值优化所用时间是12.701 8秒,LK方法用时1.552 6秒,EM方法用时0.046 8秒,可见EM方法的运算效率远高于EHO方法和LK方法。类似的结论在数据B和C中也得到体现。

表2 三种算法的优化所用系统时间
六、在上证A股市场中的应用
股票市场日成交数据比模拟生成数据要复杂得多。单支股票的日买卖单数据,在一个季度或年度中可能会发生急剧变化,从日买卖单几万手上升至几百万手。因此,实际交易数据数量级大,且在样本区段内变化大,这导致在估计模型参数时极易出现数值溢出,并且对参数初始值的设定变得更加敏感。
为了进一步检验本文所提出的EM算法与EHO、LK算法的适用性,本文以2014年上证A股市场所有正常交易的股票为研究对象,剔除了长期停牌的股票后,保留了942支股票。数据观测时期从2014年1月3号到2014年12月31号,市场交易天数为245天,但大部分股票因上市公司召开股东大会正常停牌一天,因此其交易天数为244天。少部分股票因其他原因停牌,其交易天数可能会少于244天,所有入选的样本股交易天数均大于150天。具体的日成交数据来自Wind数据库以及新浪财经数据平台,买卖单的方向由交易系统自动标定。分别用三种方法估计出各支股票的PIN,结果发现:EHO方法因为数据溢出未能给出任意一支股票的PIN,虽然LK方法和EM算法能够计算出各支股票的PIN,但是由于LK方法的优化结果很多是局部最优解,因此后面两种算法所求解出的PIN存在较大差异。从两种方法估计结果的对比分析(表3)可以发现,针对相同的股票、相同的交易数据,LK算法所估计的PIN相比EM算法的估计结果而言,无论是中位数还是均值都偏小,由此可见LK算法在实际应用中存在系统性下偏。

表3 LK算法和EM算法的PIN估计结果比较
七、结 论
知情交易是市场微观结构中最为重要的概念之一,市场知情交易水平的度量一直是该领域学者极为关注的问题。自从Easley等提出EKOP模型之后,学者对知情交易水平的测算便集中于对知情交易概率(PIN)的估计[1]。由于交易数据的特殊性,传统的估计方法在实际操作中存在一些缺陷,导致估计结果不准确甚至无法得到估计结果。本文的研究发现,即使在经过Easley等以及Lin等人的改进后,PIN的估计仍存在一些传统方法不可克服的障碍[8,12]。
本文借鉴EM算法的思路,重新设计了对EKOP模型中参数的估计方法,同时根据EKOP模型中参数所服从的矩条件,对参数的初始值做出合理设定,在此基础上给出PIN的估计。通过对模拟数据和实际交易数据的估计发现,本文所提出的EM算法相比Easley等和Lin等所提出的因子化方法,在避免数值溢出和估算效率方面具有明显优势,并且Lin等因子化的方法所估计出的PIN相比EM算法的估计结果存在系统性低估。
[1] Easley D N,Kiefer N M,O'Hara M,et al.Liquidity,Information,and Infrequently Traded Stocks[J].Journal of Finance,1996,51(4).
[2] 韩立岩,郑君彦,李东辉.沪市知情交易概率 (PIN) 特征与风险定价能力[J].中国管理科学,2008(1).
[3] 陈小林,王玉涛,陈运森.事务所规模、审计行业专长与知情交易概率[J].会计研究,2013(2).
[4] 陈洁,巴曙松.非知情交易者比例与股市暴跌之间的关系——基于中国A股面板数据的实证研究[J].云南财经大学学报,2014(5).
[5] 王建峰,郭华,潘炳红.AH股市场中知情交易信息传递效率比较研究[J].南开经济研究,2014(3).
[6] Brockman P,Chung D Y.Informed and Uninformed Trading in an Electronic,Order-Driven Environment[J].Financial Review,2000,35(2).
[7] Brown S,Hillegeist S A,Lo K.Conference Calls and Information Asymmetry[J].Social Science Electronic Publishing,2004,37(3).
[8] Easley D,Hvidkjaer S,O′Hara M.Factoring Information into Returns[J].Journal of Financial and Quantitative Analysis,2010,45(2).
[9] Ersan O,Alici A.An Unbiased Computation Methodology for Estimating the Probability of Informed Trading[J].Journal of International Financial Markets Institutions & Money,2016,43(C).
[10] Easley D,Hvidkjaer S,O'Hara M.Is Information Risk a Determinant of Asset Returns?[J].Journal of Finance,2002,57(5).
[11] Vega C.Stock Price Reaction to Public and Private Information[J].Journal of Financial Economics,2006,82(1).
[12] Lin Hsiou-Wei William,Ke W-C.A Computing Bias in Estimating the Probability of Informed Trading[J].Journal of Financial Markets,2011,14(4).
[13] Jackson D.Estimating PIN for Firms with High Levels of Trading[J].Journal of Empirical Finance,2013,24(3).
[14] Gan Q,Wei W C,Johnstone D.A Faster Estimation Method for the Probability of Informed Trading Using Hierarchical Agglomerative Clustering[J].Quantitative Finance,2013,15(11).
[15] Glosten L R,Milgrom P R.Bid,Ask and Transaction Prices in a Specialist Market with Heterogeneously Informed Traders[J].Journal of Financial Economics,1985,14(1).
[16] Yan Y,Zhang S.An Improved Estimation Method and Empirical Properties of the Probability of Informed Trading[J].Journal of Banking & Finance,2012,36(2).

