产能过剩到供给侧改革视角下一般制造业全要素生产率演变研究
——以北京为例
林陟峰,何维达,2(.北京科技大学 东凌经济管理学院,北京 00083;2.新疆财经大学 经济学院,新疆 乌鲁木齐 83002)
一、引 言
目前中国正推行供给侧结构性改革,以化解一般制造业中存在的产能过剩问题。产能过剩问题的发展和供给侧改革的治理历程大致可分为四个阶段*1978—1995年因居民收入水平低下导致的部分产品过剩不同于本文讨论的产能过剩,因此本文没有将这一阶段纳入实证研究范围。:第一阶段为1996—2002年,产能过剩初显。中国政府采取紧缩的经济政策缓解通货膨胀,同时亚洲金融危机的冲击导致市场疲软、库存增加以及国内市场低迷的消费和投资引发产能过剩[1]。第二阶段为2003—2007年,产能过剩与产能不足并存。中国加入世界贸易组织后深化对外开放,一般制造业迎来大规模投资建设的同时开始出现产能利用率低的问题,而部分劳动密集型和出口导向型的一般制造业却出现了产能不足[2-3]。第三阶段为2008—2012年,产能过剩加剧。为应对美国金融危机,中国政府出台了“四万亿”投资计划,基建和地产等行业的蓬勃发展与企业投资的“潮涌现象”加剧了一般制造业的过度生产[4]。第四阶段为2013年至今,供给侧结构性改革阶段。中央和地方出台各项去产能、去库存政策,大力治理产能过剩问题[5]。分析一般制造业在产能过剩各阶段的投入产出情况和全要素生产率变化,有助于推进供给侧结构性改革的实施。
二、文献综述
国内外学者就制造业全要素生产率(Total Factor Productivity,TFP)演变展开了丰富的研究。研究内容上,主要集中于时间和空间两个维度的TFP演变研究,包括制造业TFP及分解效率值的测算及随时间演变的原因分析、制造业TFP空间分布的演变及收敛性分析。杨汝岱测算得到1998—2009年间中国制造业的全要素生产率年均增长3.83%,环比年均增长3.35%,发现改善资源配置效率是进一步提高制造业增长的新模式[6]。汪辉平等则分别对中国工业和制造业企业的TFP展开实证研究,发现TFP快速增长主要依靠技术进步带动[7-8]。沈能则采用DEA-Malmquist指数法对1985—2003年间中国制造业TFP及其空间分布特征展开实证研究,发现东、中和西部地区制造业TFP以及技术进步增长率差距呈发散趋势[9]。研究视角上,从宏观到微观依次有针对一国制造业或工业整体的TFP演变研究、针对地区或省市的制造业TFP研究、关注制造业细分行业的TFP演变研究,再到关注微观制造业企业的TFP演变研究。
研究方法上,TFP的测算方法主要有四种,分别是回归生产模型、随机前沿分析(Stochastic Frontier Analysis,SFA)、指数法和数据包络分析(Data Envelopment Analysis,DEA),前两种为参数方法,后两种为无参数方法,两种方法各有优劣。参数方法需要事先设定生产函数形式,估计过程考虑了随机误差项即非投入影响因素,同时能对估计参数和模型本身进行检验。运用SFA方法进行TFP研究的文献普遍采用的是Battese和Coelli提出的随机前沿模型,该模型对技术无效率项的数学形式和技术无效率项与随机项的概率分布做出假设[10-11]。非参数方法能测算多投入多产出情况下的TFP,还可采用Malmquist指数法将TFP分解为规模效率、纯技术效率、技术变动进行深入探讨,但没有考虑随机误差,影响效率估计效果是对TFP的有偏估计[12]。
综合看来,在研究内容上现有研究多是探讨长期内中国制造业的TFP演变,较少有文献专门讨论从产能过剩伊始至供给侧改革期间制造业TFP的变化;在研究视角上,针对制造业细分产业的TFP研究中,较少有研究探讨深受产能过剩困扰的一般制造业TFP演变情况。鉴于此,本文选择2000—2014年一般制造业18个细分产业面板数据,采用SFA方法和Kumbhakar提出的全要素生产率测算与分解方法,对一般制造业全要素生产率的演变展开实证研究[13]。北京作为首都常是经济政策的先行地,因此以北京一般制造业为例展开研究具有代表性,也可为其他省市的研究提供借鉴。
三、数据处理与指标选择
(一)数据处理
北京一般制造业细分产业可得数据的最早年份为1999年,考虑本文所用模型方法需进行增量计算,因此将考察期定为2000—2014年,这一时期跨度也较好地涵盖了产能过剩问题发展的四个阶段。由于缺失1996—1998年的数据,因此本文研究中产能过剩第一阶段实际包含年份为2000—2002年。一般制造业细分产业的划分标准采用北京市统计局在《国民经济行业分类标准》(GB/T4754-2011)基础上进行调整归并后的制造业分类。一般制造业可分为都市制造业和基础制造业,其中都市制造业涵盖14个细分产业,基础制造业涵盖8个细分产业。因为烟草制造业、废弃资源和废旧材料回收加工业、化学纤维制造业数据缺失严重,而其在一般制造业工业总产值中占比极低,所以对这3个产业数据做删除处理。塑料制品业和橡胶制品业自2012年起合并为塑料和橡胶制品业,因此对2000—2011年这两个细分产业的数据进行合并处理,最终确定了18个细分产业,具体产业分类见表1。

表1 一般制造业分类
注:资料来源于北京市统计局网站。
(二)指标选择
本文选择了3个投入产出指标,分别是产出指标工业总产值(Y)、投入指标资本存量(K)和从业人员年平均人数(L)。工业总产值反映了产业整体的产出情况,本文选取历年《北京统计年鉴》中的工业总产值(当年价格)作为该指标原始数据。为确保数据可比性,采用历年《中国统计年鉴》提供的工业生产者出厂价格指数进行平减,统一调整为以2000年为基期的不变价工业总产值数据。资本投入用资本存量指标衡量,本文选取历年《北京统计年鉴》提供的分行业固定资产合计来代表资本存量。固定资产合计是存量指标,它包括固定资产扣除累计折旧后的净值和当期新增固定资产投入,采用历年《中国统计年鉴》提供的固定资产投资价格指数进行平减,统一调整为以2000年为基期的不变价固定资产合计数据。选择从业人员年平均人数来反映劳动力投入情况,数据源自历年《北京统计年鉴》提供的分行业从业人员年平均人数。
四、模型方法
(一)构建随机前沿生产函数
本文采用Battese和Coelli构建的SFA模型[10-11],并参考Kumbhakar的模型设定[13],将时间趋势变量t作为自变量引入随机前沿模型中,具体模型形式如下:
yit=f(xit,t;β)exp(-uit+vit)
uit=uiexp(-η(t-T))
(1)
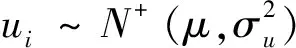
假设取对数后式(1)中随机前沿生产函数为超越对数生产函数形式,如式(2)所示:
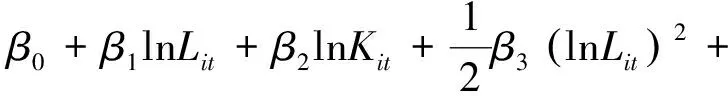
(2)
之后,本文进行三轮估计以确保随机前沿生产函数具有参数显著性,运用Frontier 4.1 进行运算,结果如表2所示。模型(a)即为式(2)所示的超越对数生产函数形式,从结果可知β4、β5和β8的参数估计值不显著,难以通过t检验,需要对生产函数形式进行调整,因此删去显著性最低的系数β8,构建模型(b),进行第二轮估计;第二轮估计结果显示,β3、β4和β5的估计值不显著,难以通过t检验,但其中β3的t检验值已十分接近显著性水平为10%、自由度为261的单侧t检验临界值,因此生产函数形式的调整主要考虑β4和β5,删去其中显著性较低的β4构建模型(c),进行第三轮估计;第三轮估计结果显示大部分系数估计值通过了显著性水平为1%的t检验,β5通过了显著性水平为10%的t检验,β3的t检验值接近显著性水平为10%、自由度为262的单侧t检验临界值,因此从参数显著性角度考虑,选择模型(c)作为本文研究的北京一般制造业随机前沿生产函数是合适的。
为进一步确保随机前沿生产函数结构形式的适宜性,本文参考Kim和Han所用的方法对模型(c)的结构形式进行如下假设检验[14]:
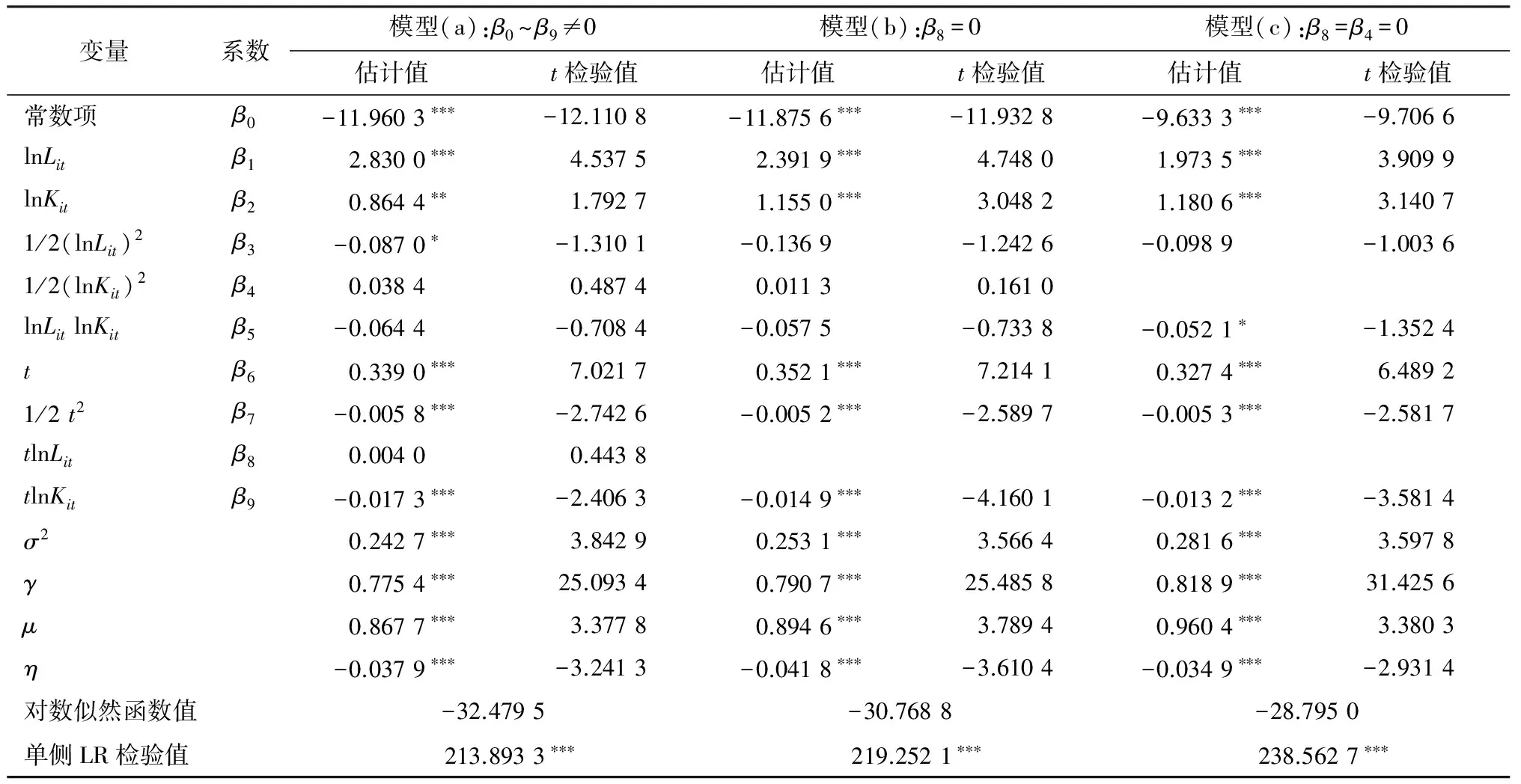
表2 北京一般制造业随机前沿生产函数估计结果
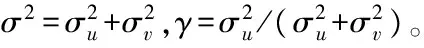
1.H0:γ=μ=η=0,技术无效率不存在,生产函数不包括随机前沿参数。此时实际产出与前沿面最优产出的差距来源于随机误差项,使用普通最小二乘法即可进行估计。
2.H0:η=0,技术无效率不随时间变化。
3.H0:β6=β7=β9=0,技术进步不存在,随时间发展技术不存在变动。
4.H0:β9=0,技术进步是希克斯中性的,即产出增长型技术进步。
5.H0:β3=β5=β7=0,此时生产函数是柯布—道格拉斯生产函数。
上述假设可通过似然比检验进行检验,其统计量LR如式(3)所示,L(H0)和L(H1)分别是原假设和备择假设下的对数似然函数值。LR近似服从卡方分布,自由度为受限变量个数。当原假设包含γ=0时,LR近似服从混合卡方分布,对假设1的检验适用这一情况。表3呈现了上述检验结果,结果显示1至5的原假设均被拒绝,结合前文参数显著性检验的结果,可知模型(c)形式的随机前沿生产函数适宜本文对北京一般制造业全要素生产率的研究,因此本文所用的随机前沿模型具体形式如式(4)所示。
LR=-2[L(H0)-L(H1)]
(3)
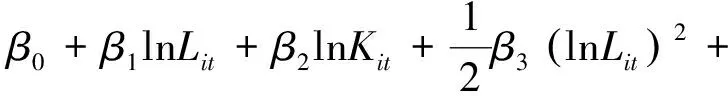
uit+vit
(4)
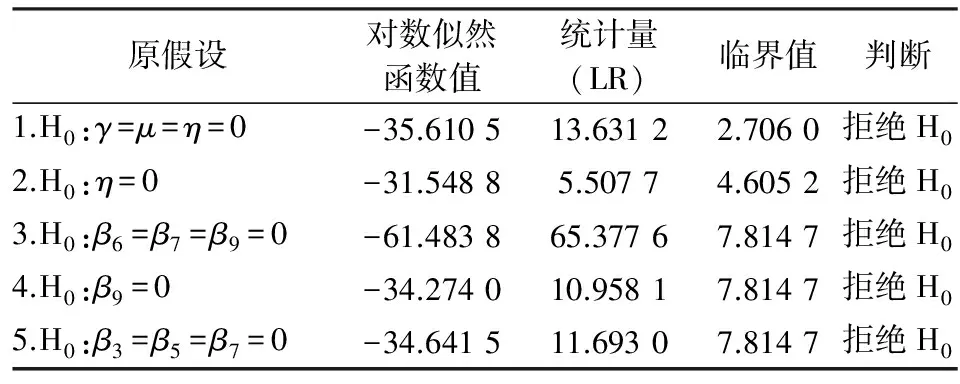
表3 随机前沿生产函数结构形式检验结果
注:表中原假设1、3、4和5呈现的是5%置信水平下的临界值,原假设2呈现的是10%置信水平下的临界值。
(二)全要素生产率测算与分解
确定随机前沿生产函数后进行全要素生产率(TFP)测算与效率分解,TFP可进一步分解为技术进步(TC)、技术效率(TEC)、规模效率(SEC)和配置效率(AEC)。要素价格数据可得性低导致AEC难以计算,研究中一般只将TFP分解为前三项。本文的投入要素固定资产合计和从业人员年平均人数各年的分行业要素价格数据缺失,因此将TFP分解为TC、TEC和SEC。TFP测算和分解方法参考Kumbhakar的研究[15]。

(5)
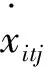
技术进步:
(6)
技术效率:
(7)
规模效率:
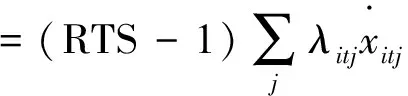
(8)
规模收益:
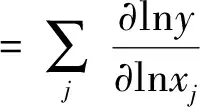
(9)
五、结果分析
(一)北京一般制造业整体TFP分析
从表4结果可知,2000—2014年北京一般制造业TFP均值为65.43%,四个阶段的TFP依次为72.63%、64.18%、64.83%和59.27%。伴随着产能过剩问题的初步显露、逐渐爆发和着手治理,北京一般制造业的TFP呈现波动恶化的趋势,投入产出水平逐渐偏离最优生产前沿面。
从效率分解值看,TFP主要依靠TEC和TC拉动,TEC对TFP贡献最大,SEC对TFP贡献最小。在样本期内TC逐渐递减表明随着时间发展技术进步带来的生产前沿面的移动程度逐渐变小。一般制造业经历了漫长的发展已进入一个相对成熟的发展阶段,生产技术相对稳定,因此科技创新带来的生产前沿面移动能力变弱。另一方面,北京成功举办奥运会及近年空气污染等环境问题的治理,都对北京一般制造业生产技术提出了更为严苛的要求。企业生产需要绿色地进行生产,这在一定程度上会表现为绿色生产技术改进,但最优产出水平下降。TEC呈现波动递减的趋势,样本期内均值为55.34%,最高值也仅有62.18%,说明北京一般制造业的生产没有充分发挥其技术潜能,出现了技术能力的闲置;SEC在样本期内剧烈波动,最高值为3.24%,最低值为-9.43%,均值为-0.82%;产能过剩的第一阶段和第二阶段的SEC均值为-0.17%和-3.67%,一般制造业陷入盲目投资和重复建设中,资本和劳动不合理的大规模投入拉低了TFP;产能过剩的第三阶段和第四阶段SEC均值为1.03%和0.67%,随着产能过剩问题的爆发和着手治理,一般制造业要素投入愈发谨慎,带来要素投入的规模效率得到改善。
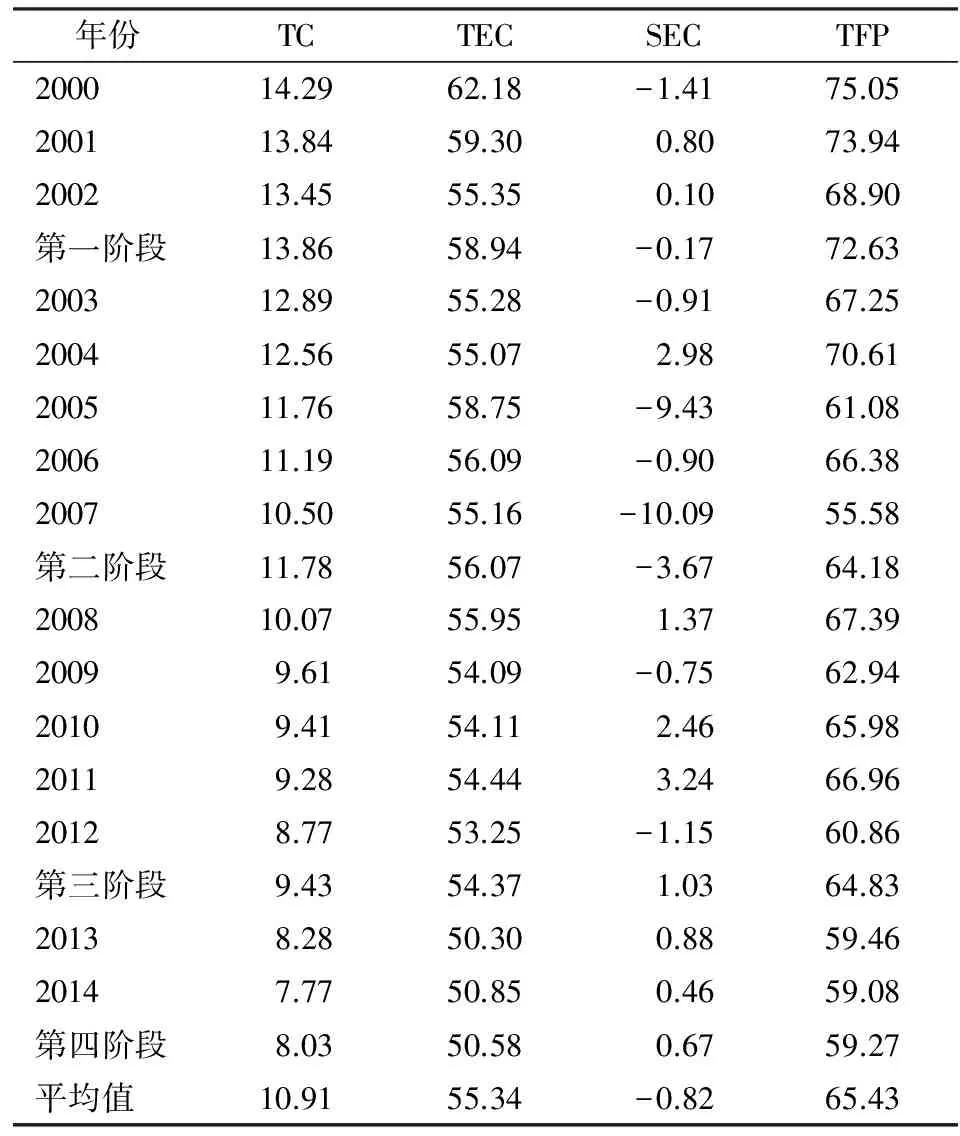
表4 北京一般制造业TFP及效率分解值 单位:%
注:表中数据由作者计算整理所得,其中各年的TC、TEC、SEC和TFP是各个细分产业按其工业总产值占比为权重的加权平均值,各阶段的TC、TEC、SEC和TFP为该阶段所包含年份的各项均值。
(二)各阶段细分产业TFP分析
表5报告了一般制造业的两大产业都市制造业和基础制造业在四个阶段的TFP及效率分解值。整体看来基础制造业的TFP大幅好于都市制造业,在第四阶段二者的差距达到19.26%。都市制造业和基础制造业TFP的差距主要源于效率分解值TEC。基础制造业包含的细分产业主要是冶金、化工等重工业,其生产流程大多使用大型机器和设备。其对技术的利用主要体现为生产线、机器设备和工艺的充分使用,在有充足的资本投入下基础制造业较容易实现技术充分使用。而都市制造业包含的细分产业主要围绕都市生活的各个方面,其生产过程受人为因素影响较大,需要更多的借助人为因素间接地实现技术使用。本文的计算结果显示样本期内各年λL<λK*作者计算了各个细分产业各年和各阶段的资本和劳动的产出弹性。因为表格篇幅较大,所以在文中没有呈现,如需要可向作者索取。,即劳动的产出弹性低于资本的产出弹性,因此表现为都市制造业的TEC较低。
从第一阶段到第四阶段看,都市制造业和基础制造业的TFP均呈现下降趋势,下降幅度分别是22.32%和17.65%,说明愈发严重的产能过剩严重扭曲产业的投入产出。TC随着产能过剩的阶段发展均呈现下滑态势, 主要原因是一般制造业本身技术和工艺已比较成熟。TEC随着产能过剩的阶段发展均呈不断大幅下降态势。都市制造业第四阶段TEC相较第一阶段降低了33.97%,逐阶段的下降比率为10.86%、15.33%和12.51%。基础制造业第四阶段TEC相较第一阶段降低了20.14%,逐阶段的下降比率为6.27%、8.63%和6.75%。随着产能过剩愈发严重,大量的产品库存和未被市场消化的产能影响了正常生产,使产业产出迫于市场压力偏离最优生产前沿面。四个阶段中都市制造业和基础制造业的SEC不断波动变化,说明产业受产能过剩和市场影响不断调整其资本和劳动的投入。
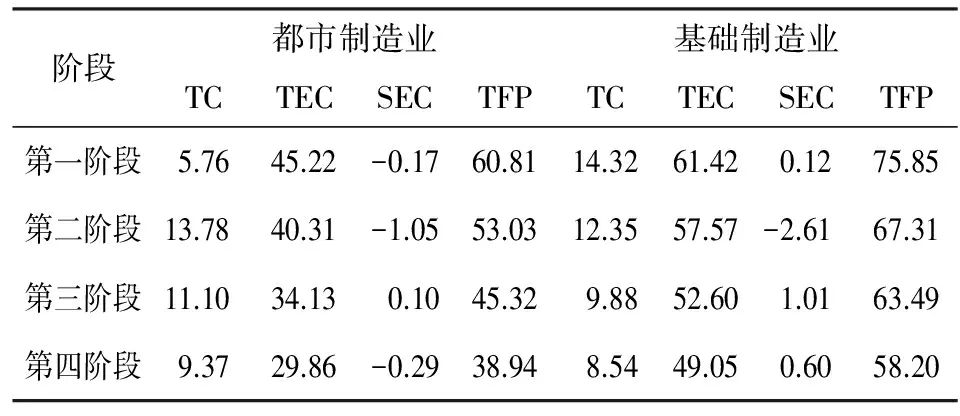
表5 四个阶段都市制造业和基础制造业TFP及效率分解值 单位:%
表6所示为各细分产业的TFP及效率分解值。细分产业中石油加工、炼焦及核燃料加工业A14、有色金属冶炼及压延加工业A18和农副食品加工业A1的TFP排名最高,投入产出情况较好;木材加工及竹、藤、棕、草制品业A13、塑料和橡胶制品业A11和印刷业和记录媒介的复制A9的TFP较低,在18个细分产业中处于靠后位置。
从效率分解值TC来看,各细分产业之间差异不大,TC平均值为12.27%,在样本期内各细分产业的技术发展速度较为接近。各细分产业TFP的效率分解值中TEC对TFP贡献最大。从TEC来看,石油加工、炼焦及核燃料加工业A14、有色金属冶炼及压延加工业A18和农副食品加工业A1拥有最好的技术效率,较为充分地利用已有技术开展生产;塑料和橡胶制品业A11、木材加工及竹、藤、棕、草制品业A13和印刷业和记录媒介的复制A9的TEC最低,投入产出水平远离生产前沿面。从SEC来看,化学原料及化学制品制造业A15、非金属矿物制品业A16和纺织业A4的规模效率最佳;石油加工、炼焦及核燃料加工业A14、黑色金属冶炼及压延加工业A17和皮革、毛皮、羽毛(绒)及其制品业A6规模效率最低,其资本和劳动力的大量投入没有得到相应产出回报,反而拉低了该细分产业TFP。
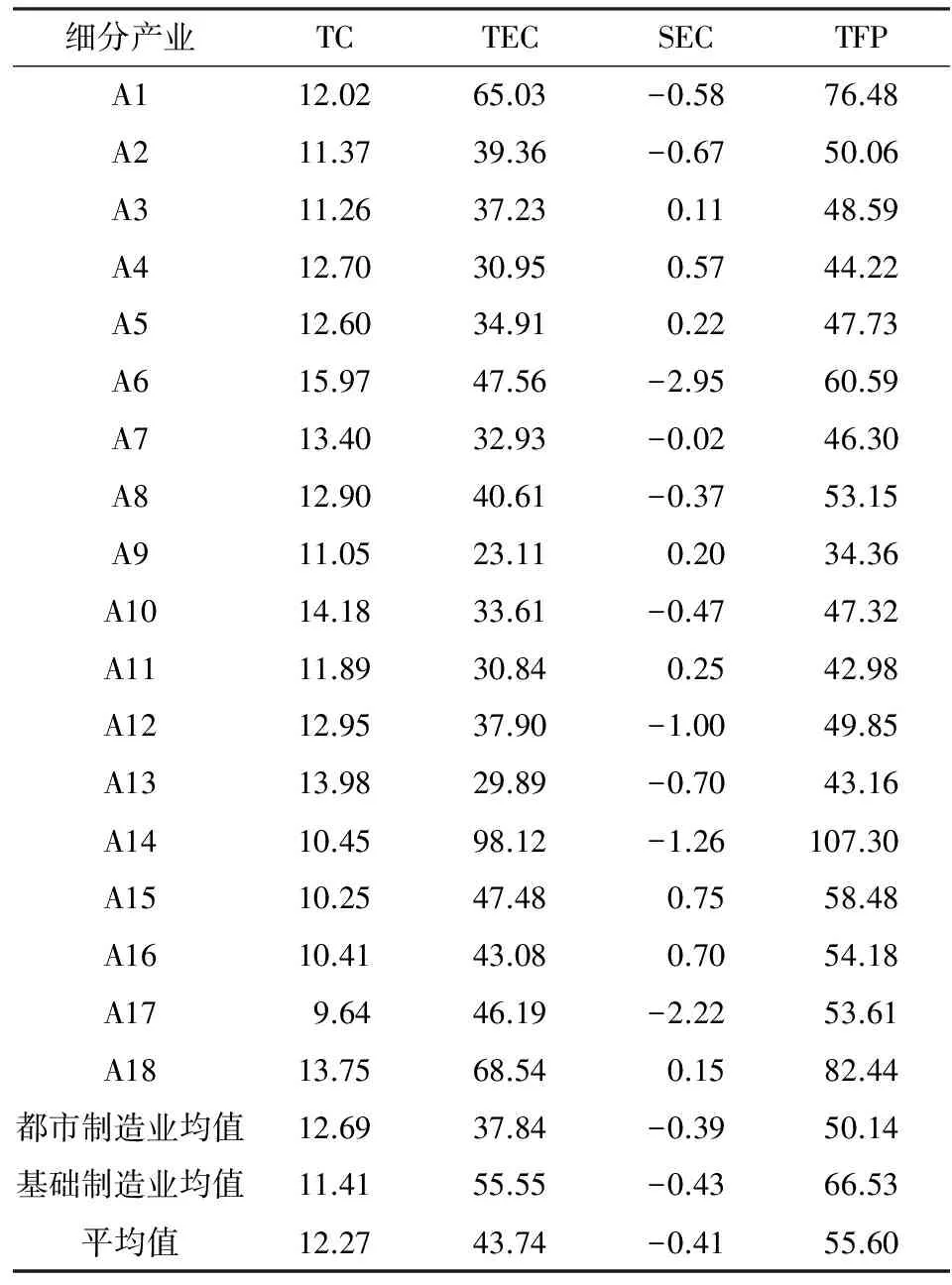
表6 北京一般制造业细分产业TFP及效率分解值 单位:%
(三)测算结果比较分析
目前还未有考察SFA实证效果的具体检验方法,为确保实证结果的可靠性,参考程慧平的研究,将SFA测算的TFP效率值与DEA方法测算的TFP效率值进行比较分析[16]。本文是从产能过剩角度展开研究,因此选择了产出导向规模报酬可变的BCC模型,选取与前文SFA方法相同投入产出指标,采用DEA-Malmquist方法进行计算*此处DEA方法计算结果主要用于考察SFA方法测算结果的可靠性,同时表格篇幅较大,因此没有在文中呈现,如需要可向作者索取。,分别运用配对样本T检验和Spearman等级相关检验对测算结果进行检验。配对样本T检验结果显示:SFA方法测算的TFP与DEA方法测算的TFP相关系数为0.577,线性相关的显著性系数为0.012,说明两种方法测算出的TFP呈高度相关关系;配对样本T检验值为-15.026,自由度为17,T检验的双尾显著性概率为0.000,表明两种方法测算的TFP具有显著性差异,这主要源于计算过程中SFA方法考虑了随机因素对产出的影响,而DEA方法仅考虑生产前沿与技术无效率项,没有考虑随机误差项。同时,受限于要素价格数据缺失,SFA方法测算时没有考虑配置效率,使得估算的效率值偏低。图1展示了样本期内各年的SFA与DEA测算结果的比较,DEA测算的TFP普遍高于SFA测算的TFP,但整体上二者呈现相似的波动下降的趋势。对两种方法测算得到的各细分产业TFP进行Spearman等级相关检验,结果显示:在5%的显著性水平下,相关系数为0.509,双尾显著性概率为0.012,表明SFA和DEA测算的细分产业TFP排序具有显著一致性。因此,整体看来SFA测算的TFP与DEA测算的TFP结果较为接近,可以认为前文测算结果有较好的可靠性。
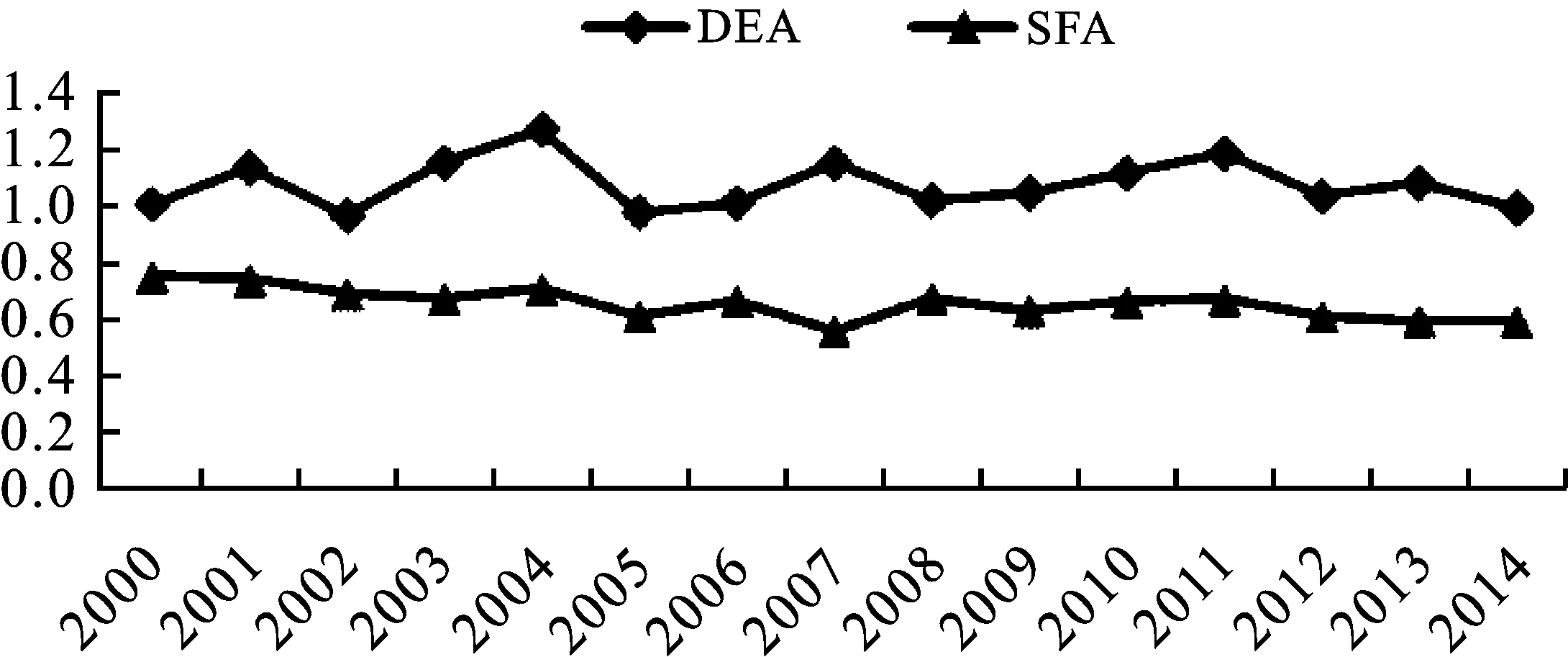
图1 2000-2014年SFA与DEA测算结果比较图
六、结语
(一)研究结论
本文采用SFA方法和Kumbhakar提出的TFP测算与分解方法对2000—2014年北京一般制造业18个细分产业的TFP进行测算和效率分解,对产能过剩到供给侧改革时期一般制造业各年、各阶段和各细分产业的TFP和效率分解值情况进行了详细的讨论和分析,主要结论如下:
第一,整个产能过剩时期,北京一般制造业TFP呈现大幅下滑趋势,2014年相较2000年TFP下降达21.03%,主要原因是时期内TC和TEC出现大幅下滑。一般制造业经过漫长的发展拥有了成熟的生产技术,通过技术进步带来生产前沿移动的速度开始放缓,同时产能过剩导致市场积压的大量产能反向影响产业生产,投入产出严重偏离最优生产水平,出现技术无效率增高的情况;第二,产能过剩各个阶段,基础制造业的TFP都好于都市制造业的TFP,主要源于基础制造业有较高的资本产出弹性和TEC,技术利用更为充分;第三,细分产业的TFP存在较大差异,其中石油加工、炼焦及核燃料加工业A14、有色金属冶炼及压延加工业A18和农副食品加工业A1在产能过剩时期拥有较高的平均TFP,而木材加工及竹、藤、棕、草制品业A13、塑料和橡胶制品业A11以及印刷业和记录媒介的复制A9的TFP较低。各细分产业间的TFP差异主要来自TEC差异,即各细分产业的技术利用充分程度不同。
(二)政策建议
针对上述分析与结论,为化解一般制造业产能过剩问题,做好供给侧结构性改革,本文提出如下政策建议:第一,持续推进一般制造业科技创新,着力改善当前一般制造企业研发投入低下的局面。政府可为技术创新表现突出的企业设置奖励金和税收优惠政策,鼓励更多企业提高研发水平。加强产学研合作,借助高校和科研机构的力量帮助企业提高科技创新能力,实现技术进步进而提高TFP。第二,对于一般制造业中产能过剩的细分产业,在做好去产能去库存的同时也要着力提高其产品的附加值。产能过剩问题中过剩的多是中低端产品,而高端产品国内市场往往供应不足需要进口,因此需要提高产品的附加值,实现产业高级化。第三,加快都市制造业的发展。北京作为首都和国际大都市,人口数量庞大,需配套发达的都市制造业才能满足城市生活的需要。当前都市制造业TFP整体偏低,因此辅助都市制造业企业充分利用现有技术以提高技术效率,开发新生产技术与工艺实现技术进步是北京城市发展提出的新要求。
[1] 高越青.“中国式”产能过剩问题研究[D].大连:东北财经大学博士学位论文,2015.
[2] 韩国高,高铁梅,王立国,等.中国制造业产能过剩的测度、波动及成因研究[J].经济研究,2011,46(12).
[3] 郑耀群,王婷.基于产能利用率测度下的中国产能过剩问题研究[J].统计与信息论坛,2017,32(3).
[4] 林毅夫,巫和懋,邢亦青.“潮涌现象”与产能过剩的形成机制[J].经济研究,2010,45(10).
[5] 乔俊峰,陈字旺.供给侧改革背景下地方政府财政支出效率的影响因素[J].河南师范大学学报:哲学社会科学版,2017,45(6).
[6] 杨汝岱.中国制造业企业全要素生产率研究[J].经济研究,2015,50(2).
[7] 汪辉平,王美霞,王增涛.FDI、空间溢出与中国工业全要素生产率——基于空间杜宾模型的研究[J].统计与信息论坛,2016,31(6).
[8] 汤学良,宗大伟.局部知识溢出与企业全要素生产率演化——基于中国制造业企业数据的研究[J].贵州财经大学学报,2017,35(1).
[9] 沈能.中国制造业全要素生产率地区空间差异的实证研究[J].中国软科学,2006(6).
[10] Battese G E,Coelli T J.Frontier Production Functions,Technical Efficiency and Panel Data:With Application to Paddy Farmers in India[J].Journal of Productivity Analysis,1992,3(1-2).
[11] Battese G E,Coelli T J.A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data[J].Empirical Economics,1995,20(2).
[12] 庞瑞芝,王亮.服务业发展是绿色的吗?——基于服务业环境全要素效率分析[J].产业经济研究,2016(4).
[13] Kumbhakar S C.Production Frontiers,Panel Data,and Time-Varying Technical Inefficiency[J].Journal of Econometrics,1990,46(1-2).
[14] Kim S,Han G.A Decomposition of Total Factor Productivity Growth in Korean Manufacturing Industries:A Stochastic Frontier Approach[J].Journal of Productivity Analysis,2001,16(3).
[15] Kumbhakar S C.Estimation and Decomposition of Productivity Change When Production Is not Efficient:A Panel Data Approach[J].Econometric Reviews,2000,19(4).
[16] 程慧平.基于DEA和SFA方法的信息服务业技术效率研究[J].科学学与科学技术管理,2013,34(4).

