经济新常态、“全面二孩”政策与生育率波动——基于真实经济周期的分析测度

张 鋆，万程成(.西南财经大学 经济学院，四川 成都 60074；.贵州财经大学 工商学院，贵州 贵阳 55005)

生育政策调整对中国人口变动及社会经济发展具有重要影响与深远意义，党的十八届五中全会提出：坚持计划生育的基本国策，完善人口发展战略，全面实施一对夫妇可生育两个孩子的政策，积极开展应对人口老龄化行动。“全面二孩”政策作为继“单独二孩”政策后的又一次人口政策调整，其目的在于进一步释放生育潜力，减缓人口老龄化压力，缓解劳动力供给问题，促进人口均衡发展。“全面二孩”政策的落地标志着中国生育政策调整步入新的历史阶段。

一、文献回顾

人口增长与经济发展的关系是人口经济学界长期争论的问题，但不同时期对这一问题的侧重点又不尽相同。生育政策调整作为现阶段中国理论界研究的重要课题，一直备受学者们的广泛关注。“全面二孩”政策尚在孕育期，就引发了学术界的激烈讨论，争论的焦点之一是二孩政策的实施能否达到生育率提高的预期效果。林毅夫(2006)对生育率的预测，秉承了“即使放松生育政策，人口生育率也不至于出现大幅度反弹”的观点。继林毅夫之后，部分学者对生育政策放开以提高生育率的预期持悲观态度，他们较一致地认为，现阶段由社会经济发展所导致的生育意愿改变已经形成比过去生育政策更强的约束，生育政策对生育率变化的制约已失去现实意义[1-2]，低于世代更替水平的生育意愿已成为一种“新常态”[3-4]。同时，诸多学者对生育政策调整仍采取审慎乐观态度。王广州等通过随机微观人口仿真模型研究全面放开二孩政策对出生人口规模的影响，预期出生人口规模在2 100万左右，同时或出现600万出生人口堆积[5]。石人炳测度全国的生育潜能存量将达到约2 000万人，其中60%左右主要集中在最初几年释放，从而不可避免地导致出生人口堆积[6]。翟振武等认为，政策调整将明显改善中国总人口未来进入负增长的趋势，增加劳动力资源的未来供给，延缓人口老龄化的进程[7]。

然而，以上的研究还存在以下局限性：一是相关文献对生育率的测度，基本建构在对中国育龄人群生育意愿的调查统计基础上[8-10]，而将理想子女数或二孩生育意愿作为实际的生育水平来进行判断存在较大偏差；二是注重微观基础而忽视宏观系统，较为孤立地看待中国的生育政策调整，没有完全将中国的生育政策调整放在新常态的背景下，或者说没有放在现阶段中国所处的宏观经济周期背景下来考虑，缺乏对生育率周期性波动的研究。

与国内相关研究比较，国外对生育率的周期性特征有较为系统的研究成果。这一方面是由于国内长期施行“少生优生”的生育政策，生育率在很大程度上受到生育政策约束，从而导致国内学者的关注点比较集中在人口增长的周期性上，而对生育率的周期性问题并不敏感。另一方面，随着超低生育率(lowest low fertility)在西方国家范围内开始蔓延，西方学界也逐渐对生育率的周期性特征给予了高度关注。

生育率的周期性特征最早可以追溯到马尔萨斯(1798)的人口过剩说，以及马克思在《经济学手稿(1857—1858)》中提出的相对过剩人口理论。虽然二者的关注点并不在人口生育率的波动上，但其研究中仍涉及到人口再生产问题，暗含了人口增长率与经济增长具有相互制约关系。国外学者通过对生育率的周期性特征进行实证检验，得出生育率具有反周期性的结论。有学者对美国1948—1975年的经验数据分析，以及Ermisch对英国1950—1985年数据观察，皆论证了这一结论，即生育率具有反周期特征[11]。值得一提的是，国外学者近期的研究结果，却基本上采取截然相反的看法，秉承生育率顺周期的观点。如McNown对美国二战之后的经验数据分析，认为生育率具有顺周期特征[12]；Adsera对OECD中23个国家1960-1997年的经济数据进行分析，研究表明生育率下降与失业率下降同步，从而说明生育率是顺周期的[13]；Örsal和Goldstein基于Adsera的分析，扩大样本并采用面板方法，得出了与其一致的结论[14]。生育率是顺周期性还是反周期性的问题，在学术界并没有形成统一的认识。少数学者研究了大量历史数据的统计分析，提出了生育率并不存在明显周期性特征的观点，其理论根源主要来自库兹涅茨(1989)关于人口增长对经济增长是中性的结论，但是由于人口增长并不能等同于生育率增长，因此，这种观点也未能得到学界的普遍认同。

参照国外现有的研究成果，对于探讨中国“全面二孩”政策开放后，中国的生育率波动情况具有重要的借鉴意义，但其中仍存在不足：一是对生育率的周期性研究，主要从宏观层面进行考量，缺乏微观基础且鲜有传导机制的研究。二是实证方法主要是以回归分析方法为主，这就不可避免地陷入“卢卡斯批判”*卢卡斯批判是由卢卡斯提出，认为传统政策分析没有充分考虑到政策变动对人们预期的影响。问题，特别是中国正处于经济转型、结构调整、动力转换的经济新常态，为应对经济新常态提出的供给侧改革等政策导向，必然加深“卢卡斯批判”问题。

因此，本文尝试在动态随机一般均衡框架下探究中国生育率变化的微观基础，并在此基础上讨论生育政策调整的宏观效应。与现有相关文献比较，本文采取动态随机一般均衡的构建思路具有以下特点，一是可以有效缓解“卢卡斯批判”问题；二是注重微观基础与宏观系统的结合；三是基于经济周期视角系统地考察“全面二孩”政策的社会效应，避免从生育政策调整视角孤立地考察生育率的变化规律。因此，本文拟在建立一个包含生育率因素的真实经济周期(RBC)模型的基础上，通过对模型进行参数校准、经济模拟和稳定性检验，基于经济模拟的比较基础，对“二孩”生育政策调整进行理论探讨，最后总结并提出建议。

二、模型构建及均衡系统

本文通过构建一个包含生育率因素的RBC模型*值得说明的是，近年来，中国研究者给予DSGE模型越来越多的关注，DSGE模型逐步向着复杂化、精细化发展。但无论是真实经济周期(RBC)还是新凯恩斯派(NK)，为了使模拟经济达到真实数据所呈现的波动与相应的持续性效果，便不得不向模型中增加更多的冲击和摩擦。然而，笔者认为DSGE最大的优势在于能够经受住“卢卡斯批判”，但现阶段的做法，无疑是重蹈“卢卡斯批判”的覆辙。因此，本文选择较为简单的RBC模型框架进行分析。，以测度中国生育率的周期性特征。本文的构建思路为：一方面依据Leibenstein、Becker等人提出的育儿成本效益理论，以及Becker(1981)提出的新家庭经济学思想；另一方面，本文参考Crockett 等研究的一般均衡模型，将从生育孩子中获得的效用加入到家庭行为设定条件中[15]。

(一)消费者行为设定

假设经济中存在位于 [0，1] 连续的诸多家庭，家庭中存在有生育能力的夫妇并作为无限期存在的代理人。家庭从消费c、闲暇l和孩子个数n中获得效用，该代表性家庭在预算约束下实现一生效用最大化的最优化问题如下：

(1)

首先，对于一个家庭来说，育儿给家庭带来额外的消费费用φcnt，育儿成本包括用于孩子的生活、医疗和教育等费用，因此φc>0；其次，我们分别考虑家庭组织中丈夫和妻子的工作时间(hF、hM)和工资水平(wF、wM)。我们将丈夫的工作时间进行标准化处理，hF=1，妻子的工作时间由家庭选择的育儿数量及闲暇时间决定，且服从hM∈ [0，1]；再次，设定家庭t时期的投资it，kt表示t时期的资本，it是关于t时期与t-1期资本的函数it(kt，kt-1)。rt为资本投资回报率。由此，家庭的联合约束条件为：

(2)

kt=(1-δ)kt-1+it

(3)

养育孩子将花费时间并因此减少货币收入或闲暇，家庭在工作、育儿、闲暇中分配他们的时间。首先我们不在模型中考虑闲暇问题*模型中不考虑闲暇问题，是出于简化模型机制的目的。事实上，在后文中我们将加入对闲暇的考虑，加入闲暇后，模型仍具有稳健性，且并不影响最终的结果。，其次我们假设妻子在工作和育儿两者中分配时间，妻子育儿时间将随着孩子的数量增加而增加，但边际投入时间将随着孩子数量的增加而减少。

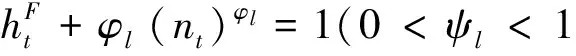
(4)

(二)厂商行为设定

设定厂商生产行为在完全市场竞争条件下，并采用CES生产函数。在本文的模型建构中，基于妻子和丈夫的工作时间、工资水平差异性的考虑，假设妻子与丈夫的劳动供给具有不完全替代性，以保证这种差异性得以体现，θ表示妻子工作时间的份额，替代弹性设定为1/(1-ρ)。由此，CES生产函数的具体形式如下：

(5)

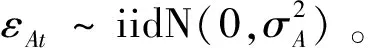
lnAt=ρAlnAt-1+εAt

(6)

厂商通过选择资本量与劳动力，以追求利润最大化：

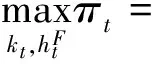
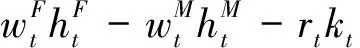
(7)

(三)最优化问题

根据家庭的效用函数以及约束条件，可以得到家庭选择的最优化问题为：

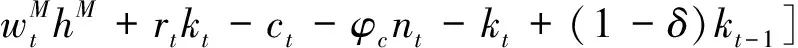
(8)

(9)

一阶条件(FOCs)为：

(10)

kt：Et[λt+1(rt+1+1-δ)]=λt

(11)

(12)

(13)

(14)

λt：yt=ct+φcnt+kt-(1-δ)kt-1

(15)

厂商行为最优化问题为：

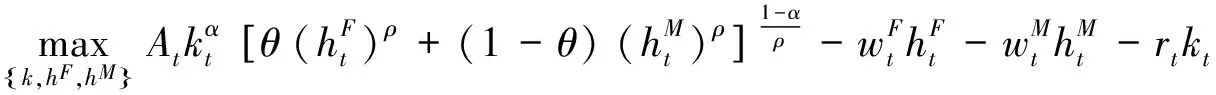
(16)

一阶条件(FOCs)为：

(17)

(18)

(19)

同时：

(20)

(21)

lnAt=ρAlnAt-1+εAt

(22)

对上述规划问题进行求解，可以得到包含要素价格{r、wF、wM}以及相关宏观变量{c、k、y、i、n、hf、h、A}的非线性动态方程系统。

三、参数估计、数值模拟与稳健性检验

(一)参数取值或估计

根据以上RBC模型的设定,需要确认的相关静态参数包括主观贴现因子β、家庭育儿的效用权重σn、育儿的时间成本系数Φl、育儿的时间成本曲率ψl、育儿的消费成本系数φc、资本份额α、资本折旧率δ、女性劳动者在生产中的权重、劳动替代弹性ρ，以及动态参数中技术冲击的一阶自回归参数ρA。

首先，对家庭的偏好参数进行取值或估计。有关国外的参数取值常常借鉴于美国数据，Galí(2007)、Liu和Phaneuf(2007)对美国的经济参数校准时，对折现率β都选择0.99这一数值，这是出于年利率 4%的考虑。国内学者对这一数据的选择，基本也是围绕0.95进行估计取值。陈彦斌等人基于国内季度数据的考虑，将折现率β设定为0.985，这就表示在稳态时季度资本收益率为1.5%，这种设定模式与美国学者的设定模式具有相似性，同时考虑了中国的具体情况[16]；陈国进等基于1978—2012年的物价水平来校准居民的主观贴现率β，将这一数值选定在0.947 7[17]。综合考虑，本文对折现率β取值选定为0.985。关于家庭育儿的效用权重σn的选择，可以根据消费c和育儿n的边际效用替代率条件和C-D生产函数关于女性劳动者的边际产出性质，估计得到家庭育儿的效用权重σ为2.04。本文对育儿的时间成本系数Φl以及育儿的时间成本曲率ψl的设定，将遵循Cooley和Prescott的设定规则，选取育儿的时间成本系数Φl=0.4，育儿的时间成本曲率ψl=0.33，设定育儿的消费成本系数φc=0.01[18]。

其次，对生产者参数进行取值或估计。关于资本份额α的取值，Gregory等曾利用中国1952—1988年的经验数据对总量生产函数进行估计,发现规模报酬不变的C-D生产函数适用于中国经济，他们估计得到的资本份额为0.55[19]，而Christian等(2005)参照美国经济状况，对资本份额α的取值设定在0.36。国内学者对资本份额的估计基本在0.5左右，例如张军(2002)对资本份额的估计值为0.499，王小鲁和樊纲(2000)估计的资本份额为0.5，国内学者的估计是基于对稳态时资本对产出的贡献率的考虑，资本对产出的贡献率为0.5比较符合中国经济情形。本文资本份额α的选取也遵从这一规则，设定α=0.5。关于资本折旧率δ，本文选取季度资本折旧率为0.025,即年折旧率为10%，这一数据的选取源于国内的标准设定(陈彦斌，2009)。国外对资本折旧率δ的设定与国内大多数文献基本一致，例如Cooley和Prescott(1995)对这一数值的估计为0.113。有关技术的结构参数校准，国内外的一般性设定，都是将这一指标进行标准化处理，因此可以设定稳态时A=1。本文关于劳动替代弹性ρ的选取，参照Acemoglu(2004)的取值设定ρ=0.65。而关于女性劳动者在生产中的权重，本文参照Lagerborg(2015)的计算方法，根据家庭男性劳动者和女性劳动者的工资比例，对θ设定值为0.35。

对于外生冲击ρA的选取，Cooley和Prescott(1995)对这一数值的设定为0.9。国内胡永刚、刘方(2007)基于季度数据考虑，选定ρA=0.95，标准差为0.023。陈国进等(2014)参考相关外文文献关于一阶自回归参数均服从贝塔分布的做法，对ρA进行了贝叶斯估计，得到ρA的后验置信区间为 [0.990，0.996]。本文对该数值的选取为0.9。

综上所述，对各参数的设定值进行归纳，结果如表1所示。

表1 参数的估计结果

(二)经济模拟

笔者对以上模型进行经济模拟，分别得到总产量、消费、劳动供给以及生育率等变量对技术正向冲击的动态反应结果图*由于篇幅受限，文中省略了结果图，有兴趣的读者请和作者联系。。面对外生技术冲击，经济系统处在稳态的位置被打破，宏观经济变量出现对稳态的偏离，然后经过一定时间又回到稳态。这一波动过程在本文的模型中也是显著的，当经济系统面临技术1%正向冲击时，总产量、消费、劳动力以及生育率等变量出现对稳态位置的偏离，经过一段时间后它们又回到稳态。

根据这一结果，首先分析总产量对外生技术正向冲击的动态效应。面对外生技术的1%正向冲击，总产量的反应在当期立即上升到一个最大值，即总产量正向偏离值达到最大，随后以较快速度下降，在第15期左右下降速度开始放缓，大概在第40期回到初始状态，并保持稳定。其次分析劳动供给对技术正向冲击的动态效应。面对外生技术1%正向冲击，劳动供给对稳态偏离值的变化是：当期跳跃到一个负值，接着以较快的速度继续下降，并在第7期下降到最小值，此后以较为缓慢的速度向初始状态运动，大约在40期之后回到初始状态。而观察女性劳动供给的反应，其运动轨迹与总劳动供给的运动轨迹大致相同，只是这一波动过程更加剧烈，对外生技术冲击的反应也更为强烈。最后我们考察生育率面对外生技术1%正向冲击时，对稳态偏离的运动轨迹：生育率在当期跳跃到一个正值，随后处于快速上升期，在第8期达到最大值，接着以较为平滑的速率开始下降，在大约40期之后回到初始值状态，并保持稳定。

① 本文在这里并没有给出φc=0.8%时，各关键变量面对外生技术冲击的脉冲响应图像。其原因在于消费成本系数φc从1%调整到0.8%后，模拟结论并没有发生明显变化，与φc=1%的脉冲响应基本一致，因此，在这里不再赘述。

② 表2中变量从上到下依次代表产出的标准差、消费相对产出的标准差、投资相对于产出的标准差。

本文通过对育儿的消费成本系数φc进行调整，将其设置在一个较低水平(φc=0.8%)①和更低(φc=0.5%)的水平后进行模拟，从而观察不同的消费成本系数下外生技术冲击对关键变量的影响。在φc=0.5%时，经济系统面临技术1%正向冲击时，总产量、消费、劳动力以及生育率等变量出现对稳态位置的偏离，经过一段时间后它们又回到稳态的反应过程。

首先，分析总产量对外生技术正向冲击的动态效应。面对外生技术的1%正向冲击，总产量的反应在当期立即上升到一个最大值，即总产量正向偏离值达到最大，随后以较快速度下降，在第15期左右下降速度开始放缓，大概在第40期回到初始状态，并保持稳定。其次，分析劳动供给对技术正向冲击的动态效应。面对外生技术1%正向冲击，劳动供给对稳态偏离值的变化是：当期跳跃到一个正值，接着以较快的速度下降，大约在第8期下降到初始值，在第9期接着下降，直到第12期达到最小值，此后以非常平缓的速度向初始状态运动，大约在31期回到初始状态并保持稳定。而观察女性劳动供给的反应，其运动轨迹与总劳动供给的运动轨迹大致相同，只是这一波动过程更加剧烈，对外生技术冲击的反应也更为强烈。再次，考察生育率面对外生技术1%正向冲击时，稳态偏离的运动轨迹为：生育率在当期跳跃到最小值，随后处于快速上升期，在第9期左右回到初始状态，从第10期到第30期，分别经历了从上升到下降的过程，并始终处在对初始值微弱的正向偏离位置，在大约30期之后回到初始值状态并保持稳定。

综合上述，当育儿的消费成本系数φc分别设定为1%、0.8%和0.5%时，模拟经济系统做出了不同响应，可以得出以下结论：

1.育儿的消费成本系数高低，并不影响总产量的动态效应，在面对外生技术正向冲击时，总产量是上升的。

2.当育儿的消费成本较高时，生育率是顺周期的，面对外生技术正向冲击时，女性劳动者将减少她们的劳动供给，同时生育率会有所提高。

3.当育儿的消费成本较低时，生育率具有反周期特征，在经济繁荣时，女性倾向于增加劳动供给并降低生育率；在经济衰退时，她们倾向于减少劳动供给并增加生育率。面对外生技术正向冲击时，女性劳动者将增加她们的劳动供给，同时生育率会有所降低。

(三)含生育率的RBC模型的稳健性检验

本文从三个方面分别对含生育率的RBC模型的稳健性进行检验。首先，考察含生育率的RBC模型在引入女性劳动者闲暇变量之后的预测值与引入前是否出现显著性变化。其次，考察在引入偏好冲击之后对模型的影响并与不考虑偏好冲击的RBC模型进行比较分析。最后，对相关变量的脉冲反应进行敏感性检验。

1.引入女性劳动者闲暇的RBC模型

此时代表性家庭在预算约束下实现一生效用最大化的最优化问题为：

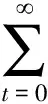
(23)

(24)

(25)

2.包含偏好冲击的RBC模型

参考Smets和Wouters的研究方法[20]，在效用函数中引入偏好冲击，则代表性家庭效用最大化问题可以表示为：

(26)

同时假定偏好冲击服从对数AR(1)过程：

lnχt=ργlnχt-1+εγ t

(27)

表2显示了包含女性劳动者闲暇的RBC模型与不包含女性劳动者闲暇的RBC模型的对比结果，以及包含偏好冲击RBC模型与不包含偏好冲击RBC模型的对比结果。对表2进行分析可知，模型中关键经济变量的模拟值均未出现明显的数值变化和符号变化，两类模型对关键经济变量波动特征的预测也基本一致。

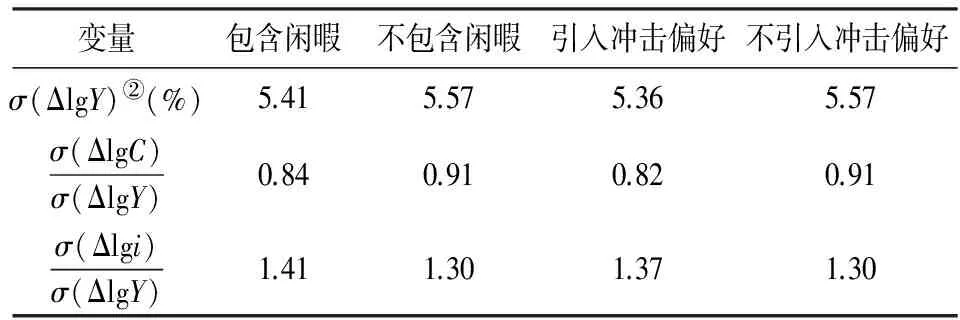
表2 含生育率的RBC模型

3.对含生育率的RBC模型中相关变量的脉冲反应进行敏感性检验

如α在[0.3，0.55]区间内不影响模型的收敛性和稳定性，育儿的时间成本系数Φl在[0.2，0.8]之间取值，育儿的时间成本曲率ψl在[0.1，0.5]之间取值。这些实验结果都表明，脉冲反应结果稳健，即各关键变量对冲击的动态轨迹的运动方向没有改变。以上试验表明，由本文构建的模型所得出结论对一些参数在一定范围内变化不敏感，这证明了模型的模拟结论在较宽泛的参数范围内是稳定的。

四、结论及政策含义

本文在动态随机一般均衡的框架下引入了生育率因素，构建了一个包含生育率的RBC模型。之后利用中国宏观数据校准模型的结构参数，并进行了数值模拟分析，通过对育儿成本系数的控制，探讨中国新常态下“全面二孩”政策放开后的生育率周期性特征。需要说明的是，这种建模思路中暗含了一种假设前提，即育儿成本系数与生育政策之间存在显著的相关性。笔者认为，在中国计划生育政策的二孩限制时期，生育政策可以内化为家庭生二孩的经济成本，家庭决策时面临的生育政策约束在一定条件下可以转化为经济约束予以考虑。2001年中国出台的《人口与计划生育法》，将超生缴纳款项作为“社会抚养费”进行了明确规定，可以作为这一假设的事实依据。

“全面二孩”政策放开，家庭生二孩的经济成本会相对生育政策调整前有所下降，因此将“全面二孩”政策转化为育儿成本下降进行分析，具有一定的合理性和可操作性。问题的关键在于，育儿成本下降程度是否显著？一种观点认为生育政策限制是中国生育率下降的主导作用(Scharping，2003；Greenhalgh和Winckler，2005)，可以侧面反映出“全面二孩”政策转化为育儿成本下降的程度显著；另一观点认为生育政策限制已不再是生育率变化的主导因素，其他社会经济因素或形成更强的约束(顾宝昌，2008；Zheng，2009；Cai，2010)，这从侧面反映出“全面二孩”政策转化为育儿成本下降的程度有限。因此，本文对模型中育儿的消费成本系数φc进行两次调整，也是为了在某种程度上反映上述两种观点，并得出以下结论：

第一，当育儿的消费成本φc从1%调整到0.5%时，育儿的消费成本处于较低水平，生育政策调整前与调整后存在显著差别。此时生育率具有反周期特征，面对外生技术正向冲击时，女性劳动者将增加她们的劳动供给，同时生育率会有所降低，且这一过程会呈现出明显的驼峰效应。考虑到中国正处于新常态时期，生育率的反周期特征意味着生育政策调整后生育率会有所提高，尤其在政策实施的最初几年会有明显释放。

第二，当育儿的消费成本φc从1%调整到0.8%时，育儿的消费成本仍然较高，生育政策调整前与调整后并无显著差别。此时生育率是顺周期的，面对外生技术正向冲击时，女性劳动者将减少她们的劳动供给，同时生育率会有所提高。参照中国正处于经济结构调整、存在经济下行压力的新常态时期，生育率的顺周期特征意味着生育政策调整后生育率在整体上不仅不会提高，反而会继续趋于下滑。

第三，通过模型构建所得到的结果，在其可能性上，为生育率的顺周期或反周期皆提供了理论基础，将两种可能性很好地包容在模型之中。在其现实性上，“全面二孩”政策开放后，育儿成本下降程度是否显著尚无定论，但结合中国当前的经济新常态特征与西方国家生育率的周期性特征考量：“全面二孩”政策对育儿的消费成本形成向下的冲击，虽能够影响中国生育率的周期性波动，但不足以产生方向性的改变。因而，本文更加倾向第二种判断，即“全面二孩”政策转化为育儿成本下降的程度有限的观点。

从长期看，生育政策调整后中国总体的生育率水平或许不会明显改变。因此，本文的政策含义在于：减缓人口老龄化压力、缓解劳动力供给、促进人口均衡发展的重任，不能仅单纯地依靠生育政策调整来承担，而应持有更审慎的态度。既然问题核心是育儿的消费成本降低，那一系列的相关配套政策及时而有效地发挥作用就显得更加重要，尤其在供给侧的结构改革中，对教育供给、医疗供给、住房供给等问题应给予高度关注。

[1] 顾宝昌，宋健，刘爽，等.二孩生育政策地区的实践及启示[J].人口研究，2008(4).

[2] Cai Y.China's Below-Replacement Fertility：Government Policy or Socioeconomic Development?[J].Population & Development Review，2010，36(3).

[3] 石智雷，杨云彦.符合“单独二孩”政策家庭的生育意愿与生育行为[J].人口研究，2014(5).

[4] 杨菊华.单独二孩政策下流动人口的生育意愿试析[J].中国人口科学，2015(1).

[5] 王广州，张丽萍.到底能生多少孩子？——中国人的政策生育潜力估计[J].社会学研究，2012(5).

[6] 石人炳.“单独二孩政策”实施初期的出生堆积及其特点[J].人口与经济，2014(5).

[7] 翟振武，张现苓，靳永爱.立即全面放开二胎政策的人口学后果分析[J].人口研究，2014(2).

[8] 王广州.独生子女死亡总量及变化趋势研究[J].中国人口科学，2013(1).

[9] 侯佳伟，黄四林，辛自强，等.中国人口生育意愿变迁：1980—2011[J].中国社会科学，2014(4).

[10] 庄亚儿，姜玉，王志理，等.当前我国城乡居民的生育意愿——基于2013年全国生育意愿调查[J].人口研究，2014(3).

[11] Ermisch J F.Purchased Child Care Optimal Family Size and Mothers Employment：Theory and Econometric Analysis[C]// C.E.P.R.Discussion Papers，1988.

[12] Robert McNown.Cointegration Modeling of Fertility in the United States[J].Mathematical Population Studies，2003，10(2).

[13] Adsera A.Changing Fertility Rates in Developed Countries：The Impact of Labor Market Institutions[J].Journal of Population Economics，2004，17(1).

[14] Örsal D D K，Goldstein J.The Increasing Importance of Economic Conditions on Fertility[R].Mpidr Working Papers，2010.

[15] Crockett J L，Fleming R K，Doepke K J，et al.Parent Training：Acquisition and Generalization of Discrete Trials Teaching Skills with Parents of Children with Autism[J].Research in Developmental Disabilities，2007，28(1).

[16] 陈彦斌，唐诗磊，姚一旻.我国价格总水平影响因素与宏观调控策略研究[J].经济研究参考，2009(65).

[17] 陈国进，晁江锋，武晓利，等.罕见灾难风险和中国宏观经济波动[J].经济研究，2014(8).

[18] Cooley T F，Prescott E C.Equilibrium Business Cycles with Idle Resources and Variable Capacity Utilization[J].Economic Theory，1995(1).

[19] Gregory C Chow，Kui-Wai Li.China’s Economic Growth：1952—2010[J].Economic Development & Cultural Change，2002，51(1).

[20] Smets F，Wouters R.An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area[J].Journal of the European Economic Association，2003(5).