不同先验下分位数回归的贝叶斯估计：实现与比较

邸俊鹏，张晓峒(.上海社会科学院 数量经济研究中心，上海 0000；.南开大学 数量经济研究所，天津 30007)

一、引 言

传统最小二乘回归模型是建立在随机变量的条件均值函数(Conditional Mean Function)基础之上的，即用一组变量来解释因变量的期望。然而，在经济学、金融学、医学、环境科学等研究领域，随机变量在任意概率水平下与解释变量的关系越来越受到重视，即考察分位数回归模型。分位数回归模型估计方法一般包括三类：第一类是直接优化法，如单纯形法和内点法；第二类是参数化方法，该方法借助贝叶斯统计理论，在得到参数估计量分布的基础上，构建置信区间并进行统计推断；第三类是与参数化相对的非(半)参数方法。本文聚焦分位数回归的贝叶斯估计方法。

贝叶斯推断在一般的线性或扩展模型中已经得到广泛的应用，尤其是针对复杂的目标函数，可以通过蒙特卡罗模拟得到参数的后验概率分布。然而，在分位数回归领域，有关贝叶斯推断的文献并不多，在2000年之前只有为数不多的文章对贝叶斯分位数回归方法及其应用进行了初步尝试[1]。Yu和Moyeed发现，可以借助曾在Koenker和Bassett的一文中使用的非对称拉普拉斯分布(Asymmetric Laplace Distribution，ALD)，将分位数回归纳入贝叶斯推断的框架，从而实现了采用贝叶斯方法分析分位数回归模型[2-3]。

Yu和Moyeed借助ALD可谓开启了贝叶斯分位数回归的参数估计之门，之后在计量经济学领域中该方法越来越受到关注。Yu、Philippe和Jin采用该方法对英国工资分布进行了研究[4]，在贝叶斯推断中，他们视待估参数为随机变量，使用MCMC方法得到参数的后验分布。通过研究发现，与传统的方法相比贝叶斯分位数回归方法有以下优势：一是尽管两种方法得到的点估计值相近，但由于传统的方法基于“渐近性质”，所以贝叶斯方法相对于频率方法得到的标准误差更小；二是贝叶斯分位数回归方法是关于因变量的全后验分布(Full Posterior Distributions)，而不是单个值，因而对估计参数的了解更全面；三是频率学派的假设检验是建立在对参数分布设定的基础之上的，而贝叶斯分位数回归是通过参数后验分布的HPD(Highest Posterior Density)进行假设检验，因而功效更高。

根据贝叶斯定理，后验密度正比于参数先验密度和样本似然函数的乘积，因而在实施贝叶斯分位数回归估计过程中，有两项关键的工作：一是设定参数的先验分布；二是通过抽样得到参数的后验分布。

参数的先验分布在贝叶斯分析中占有重要地位，它代表了研究者对参数的主观信念，无论是在贝叶斯分位数回归的参数估计还是半参数估计过程中，都涉及先验分布的设定。在先验分布的选择上，Yu和Moyeed推导得出，如果设定参数的先验分布为均匀分布，即使这种选择是不适当的(improper)，由此得到的参数的联合后验分布也是适当的(proper)[2]。因此，在贝叶斯分位数回归中，先验分布可以设定为无信息先验，如均匀分布或者方差很大的正态分布。在通常的情形下，给不同分位数下的估计参数设定统一的先验分布，然而Alhamzawi和Yu认为实际研究中高分位和低分位下参数的分布可能是不同的，因而应该采用先验势(Power Prior)的方法针对不同的分位数设定不同的先验分布[5]。

当模型参数的后验分布为熟悉的函数形式(如正态分布、Gamma分布、Beta 分布等)时，可以很容易地对相关参数的后验分布进行抽样模拟，但在一般情形下模型参数后验分布的形式是未知的，此时可以运用以下几类算法对不熟悉(非标准)的参数后验分布进行抽样模拟。常用的贝叶斯抽样算法有：Hamiltonian Monte Carlo(HMC)、Gibbs算法、M-H算法、拒绝抽样(Reject Sampling)和重要抽样算法(Important Sampling)。

在贝叶斯分位数回归方法中一些细节问题也受到人们的关注，比如关于尺度参数σ。在一般的贝叶斯分位数回归分析中都将σ设定为1，如Yu和Moyeed针对连续因变量[2]、Benoit和Poel针对离散因变量的模型[6]，而在一些研究中则认为这种设定是存在问题的，不符合金融时间序列的特征，建议将σ参数化，与其他参数一起估计[7-8]。

本文在已有文献的基础上，首先借助泊松分布实现了在STAN中对分位数回归进行贝叶斯分析，从而不仅可以灵活地选择先验分布，还可以参数化规模参数，提高贝叶斯分位数回归方法的灵活性和可操作性；然后通过模拟实验研究先验分布的设定对特定抽样算法下参数估计量统计性质的影响。

二、基于ALD的贝叶斯分位数回归估计方法

设有如下线性回归模型：

yt=Qτ(yt|xt；β)+ut

与普通最小二乘法的残差平方和最小不同，分位数回归是最小化损失函数：

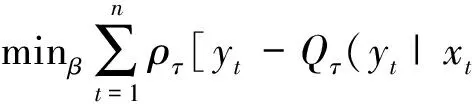
(1)

其中，Qτ(yt|xt；β)为yt在xt；β条件下的τ分位数；β为参数向量；ρτ(u)=u(τ-I(u<0))为损失函数，其中I(·)为指示函数，当满足()内条件时取值为1，否则为0。采用式(1)进行分位数回归的方法有多种，较常用的线性规划解法是直接优化分位数回归的目标函数，但直接优化一般存在困难，而采用贝叶斯方法相对容易实现。用贝叶斯方法对分位数回归进行估计，其基本步骤是：首先，通过假设分位数回归模型(1)的误差项为非对称拉普拉斯分布，写出似然函数；其次，采用基于HMC的贝叶斯估计方法可以得到分位数回归参数的抽样分布，并对抽样结果进行收敛性检验。由于对应的似然函数式连续但不可导，所以对参数求导没有解析解，在这种情况下采用HMC方法，对该后验密度进行抽样得到各个分位数上的参数β和尺度参数σ的抽样分布。

三、贝叶斯分位数回归方法的STAN实现

STAN是一套程序化的贝叶斯统计分析软件，其操作方便灵活且对用户免费。在使用过程中用户只需指定数据的似然函数和参数的先验分布，就可通过Hamiltonian Monte Carlo(HMC)抽样得到参数的后验分布，这对没有显性表达式的贝叶斯后验分布尤其重要。STAN软件中提供了正态分布、t分布、指数分布、泊松分布等多种常见的分布，用来指定似然函数和先验分布[9]，这些分布能够满足大部分的贝叶斯统计分析。然而，如果贝叶斯分析中的分布为非标准的分布，如本文中的非对称拉普拉斯分布在软件中并未提供，则需要应用一定的编程技巧和数学转换以适应于STAN程序的要求。下面介绍通过泊松分布给出非对称拉普拉斯分布的似然函数，从而实现用STAN软件对贝叶斯分位数回归的参数进行估计。

(一)用泊松分布指定非对称拉普拉斯分布

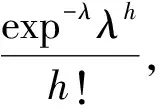
设数据的对数密度函数为li=logf(xi|θ)，密度函数为exp(li)，所以似然函数为：

一般情况下，为了保证λ为正数，可以在负对数似然函数中加一个较大的数c=10 000。一般的STAN程序如下：

model{

c<-10000

for i in 1:n{

l[i]<-…… (指定对数似然)

lambda[i]<- -l[i]+c

h[i]<-0 (所有的h取0)

}

对于表达式yi=β0+β1x+u，假设误差项u服从非对称拉普拉斯分布，ALD(μ，σ，τ)；一般情况下σ=1，待估系数为β0、β1，假定它们的先验分布是正态分布，进而可以利用泊松分布指定非对称拉普拉斯分布的似然函数，程序如下：

model {

int h[n]；

real u[n]；

real lamda[n]；

for(i in 1:n) {

h[i]=0；

u[i]=y[i]-beta0-beta1*x[i]；

lambda[i]=log(p*(1-p))+(fabs(u[i])+(2*p-1)*u[i])/2+10000；

}

如果非对称拉普拉斯分布的尺度参数σ也是未知的，待估参数是β0、β1、σ，并假设σ的先验分布是自由度为3的卡方分布，具体的STAN程序如下：

model{

int h[n]；

real u[n]；

real lamda[n]；

sigma～chi_square(3)；

for(i in 1:n) {

h[i]=0

u[i]=y[i]-beta0-beta1*x[i]

lambda[i]=log(p*(1-p))+log(sigma)+(fabs(u[i]/sigma)+(2*p-1)*u[i]

/sigma)/2+10000；

}

在具体的估计过程中，首先将上述写好的程序保存为“***.stan”文档，然后在R软件中用“rstan”调用STAN程序，从而得到待估参数的后验分布以及相关的统计量。除了用泊松分布指定非对称拉普拉斯分布的似然函数，还可以用二项分布和负二项分布指定。

(二)尺度参数是否参数化对贝叶斯分位数回归估计结果的影响

在已有的文献中，非对称拉普拉斯分布的尺度参数在估计过程中通常被指定为常数1。王新宇、宋学锋指出这种做法在实际应用中是不妥当的，并证明如果随机变量x来自非对称拉普拉斯分布ALD(μ,σ,τ)，密度函数为f(μ,σ,τ)，其方差记为φ(σ,τ)，则当σ=1时，x的方差φ(1,τ)≥8，即如果尺度参数固定为1，将导致非对称拉普拉斯分布随机变量的方差不小于8[7]，这对于实际的金融时间序列数据显然是不符合常理的，应将其视作待估的参数。

上文已经在STAN中实现了贝叶斯分位数回归估计中尺度参数的参数化。下面将通过一个模拟实验，比较尺度参数是否参数化对估计结果产生影响。

1.实验设计与抽样结果。数据生成过程为Yi=β0+β1x+εi，i=1,2,…，n，其中β0=1，β1=2，x～unif(n=n，min=0，max=10)。设定β0和β1的先验分布均为正态分布N(0，10)，尺度参数σ的先验分布为自由度等于3的卡方分布。采用HMC抽样算法共模拟10 000次，为消除初值对抽样分布的影响，去掉前5 000个抽样值。

值得说明的是，在统计推断之前需要对抽样分布进行检验，常用的检验方法有两种：一种是判断马尔科夫链是否收敛，这可以通过诊断统计量判断，也可以通过抽样的轨迹直观地判断；另一种是考察抽样值的自相关图。如果连续两次的迭代值之间相关性太强将导致抽样不能探测到参数的整个空间，测量两个抽样值相依性的标准算法是计算抽样值相隔一定滞后期L的相关系数。

图1分别给出样本容量为100时，β0、β1、σ在0.5分位点下的HMC抽样值轨迹和核密度图，结果显示三个参数的5 000个抽样值序列在某一个值的上下波动，因此抽样构成的马尔科夫链均收敛。

图2分别给出了样本容量为100时，β0、β1在0.5分位点下抽样值的自相关图*篇幅所限，σ在0.5分位点下抽样的自相关图省略，其结果类似。。从图2中可以看出，随着滞后期的增加，自相关系数趋向于零。

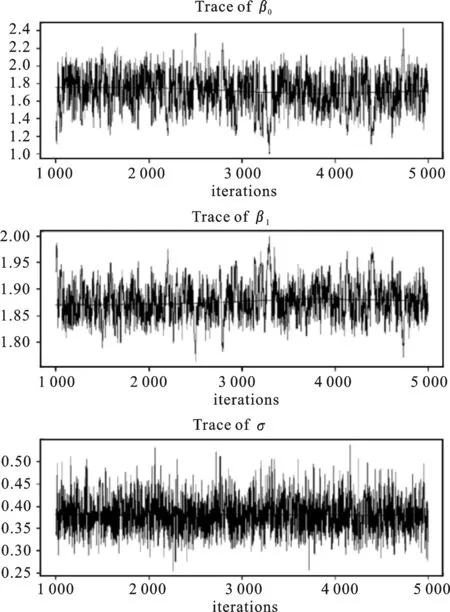
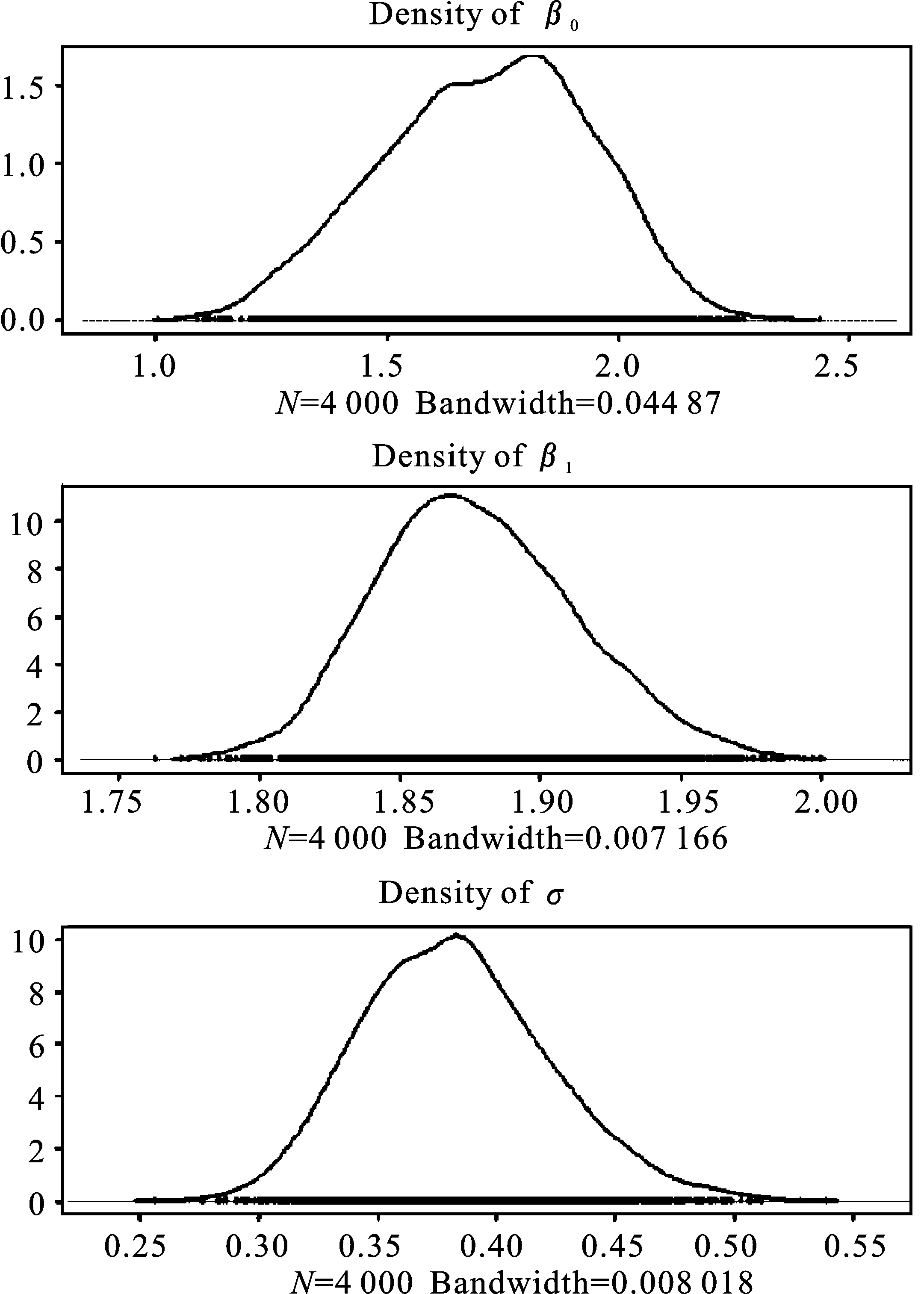
图1 β0、β1、σ抽样值轨迹和核密度图

综上，马尔科夫链收敛且自相关系数趋于零，所以在样本容量为100，各参数的贝叶斯中位数回归估计结果是可靠的。其他样本容量和分位点下的马尔科夫链均收敛，自相关系数也均趋于零。

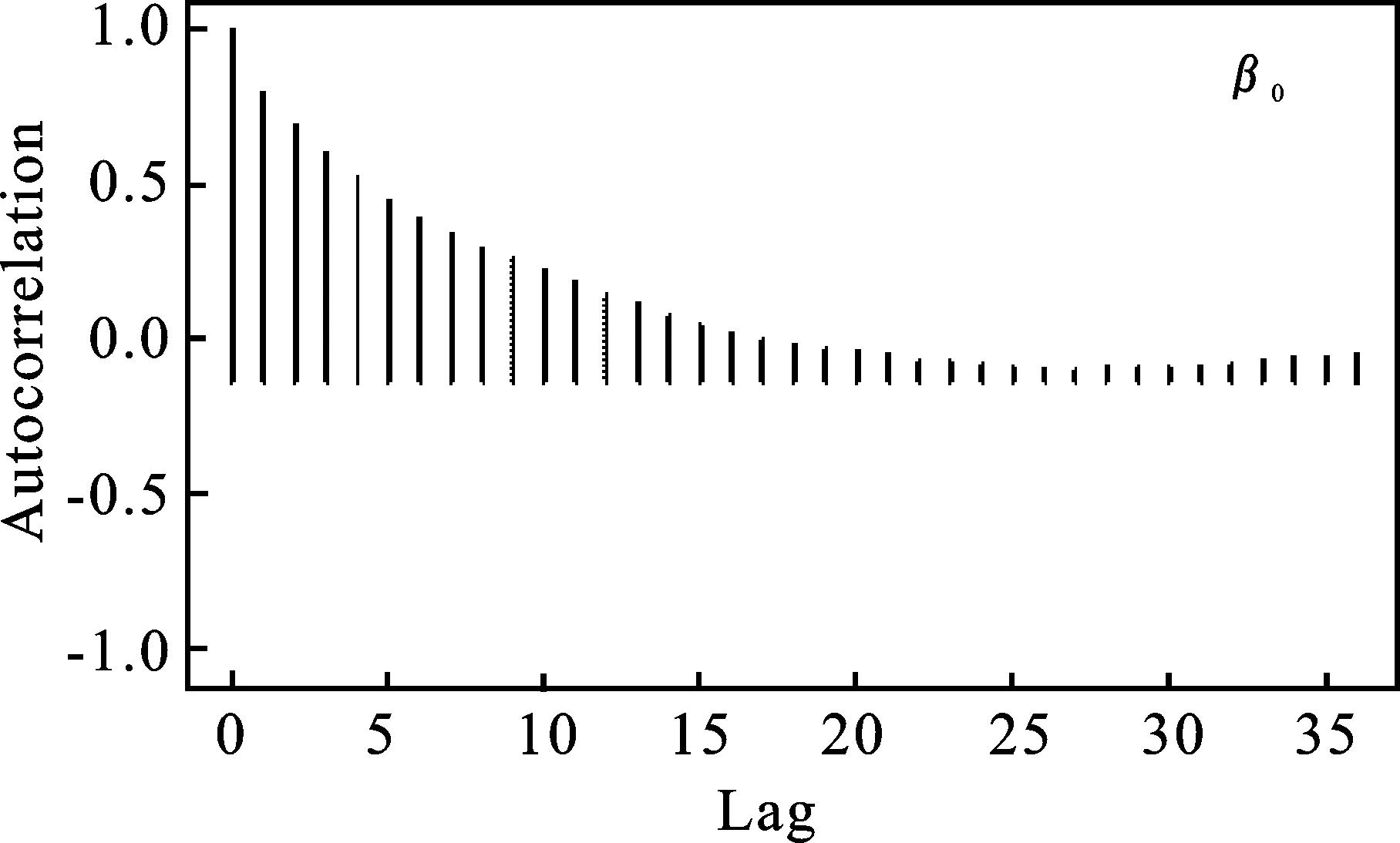
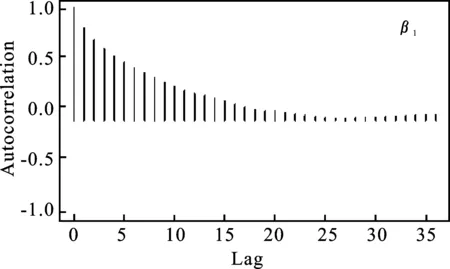
图2 β0、β1抽样值的自相关图

2.结论。比较不同样本容量下STAN软件得到β0、β1在σ参数化与非参数化下的估计结果*因篇幅所限，图表省略。如有读者需要可向作者索要。，可以发现：1)在一定样本容量、特定分位点下，当尺度变量σ被参数化时，β0和β1的抽样标准差均小于σ非参数化时各自的标准差，这表明尺度变量的参数化可以提高被估系数的估计精度，从而提高待估系数假设检验的准确性。因此，在采用HMC抽样方法进行贝叶斯分位数回归估计时应该将尺度变量σ参数化，与待估的系数一起估计，而不应该设定为常数1。2)给定样本容量，各分位点下，尺度变量是否参数化对β0和β1抽样均值与真值间的偏误没有明显的影响。因此，如果只考虑被估系数对真值的偏离程度就不必将尺度变量参数化。

此外，还可以发现：1)给定样本容量，无论在尺度变量σ被参数化还是未被参数化的情形下，β1的偏误总是小于同一分位点下β0的偏误，β1的标准差总是小于同一分位点下β0的标准差，这表明在本模拟实验给定的参数先验分布条件下，通过STAN软件得到解释变量系数估计值的统计性质要优于常数项估计值的统计性质。2)对于β1，无论是在尺度变量σ被参数化还是未被参数化的情形下，它的精度都随着样本容量的增加而提高，而β0的精度并未呈现出随着样本容量的增加而提高的特征。此外，尺度参数的精度也随着样本容量的增加而提高。

本实验的抽样估计结果是在给定参数先验分布和抽样算法的前提下得出的，而对于贝叶斯分析，先验分布的设定对抽样结果会产生影响。下面将考察不同的参数先验分布对贝叶斯分位数回归结果的影响。

四、不同先验设定下分位数回归估计量性质的比较

对于分位数回归模型，不存在标准的共轭先验分布(Standard Conjugate Prior Distribution)，因此不容易获得参数后验分布的解析表达式，但仍然可以通过模拟得到参数的估计，前提是在贝叶斯推断中参数的先验分布应该保证参数的后验分布是合适分布(Proper Distribution)。Yu和Moyeed指出，在贝叶斯分位数估计中，只要待估系数β的先验分布满足p(β)∝1，那么β的后验分布会有合适的分布[2]。王新宇、宋学锋进一步指出，当β服从不合适的先验分布时，即使尺度参数σ>0也未知，只要其密度函数f(σ)满足：

那么，参数的联合后验分布也是合适分布[7]。也就是说，在理论上先验分布可以是任意的(如果没有任何的先验信息，可以采用均匀分布)，尽管如此得到的参数联合后验分布也是合适分布。然而，已有文献中并未考察随着先验分布信息的不同，参数后验分布的统计特征有什么不同，这对于选择合适的先验信息来进行贝叶斯分位数回归估计具有指导意义。

(一)实验设计与抽样结果

下面针对一般化的形式，考察不同先验设定对估计结果的影响。数据生成过程为，Yi=β0+β1x+εi，i=1,2,…，n，除了包括截距项还包括一个解释变量，其中β0=1，β1=2，x～unif(n=n，min=0，max=10)。考虑到误差项的分布影响因变量的分布，由此可能影响不同分位点的回归系数，于是讨论误差项服从正态分布和存在异方差，即β～N(0,1)、ε～(1+x2)N(0,1)，两种不同的数据生成过程、不同的先验分布对估计结果的影响。

值得注意的是，由于回归式中不是只有截距项，因此被估参数在τ分位点下的真值受误差项的形式影响。在上面的回归式中，qτ(y)=β0+β1x+qτ(ε)，当误差服从正态分布N(0,1)时，qτ(y)=β0+φ-1(τ)+β1x，其中φ-1(τ)是标准正态分布的第τ分位数，因此被估系数的真值分别是：β0=1+φ-1(τ)，β1=2。当误差项为异方差形式时，qτ(y)=β0+φ-1(τ)+(β1+φ-1(τ))x1，即被估系数的真值分别是：β0=1+φ-1(τ)，β1=2+φ-1(τ)，其中φ-1(τ)是标准正态分布的第τ分位数。

为比较不同先验分布条件下估计量小样本性质的差异，设定参数先验分布为正态分布N(μ，σ)。下面给出三种不同的参数先验分布设定，随着σ减小，先验信息逐渐增强，具体形式如下：

先验设定1：β～N(0,100)

先验设定2：β～N(0,10)

先验设定3：β～N(0,1)

根据上述不同的数据生成过程，结合不同的先验信息，运用HMC抽样算法对模型参数进行估计。为了考察特定参数的模拟值是否为合适后验分布的合理近似，对某一先验分布假设下各个分位点下的参数抽样值轨迹和自相关图进行分析，结果表明所有情形下的马尔科夫链均收敛、自相关图均随着滞后期的增加而趋于零。图3给出了先验设定2下，样本容量为75时，参数β0和β1的抽样值轨迹和自相关图，其他情形下也类似。

(二)结论

限于篇幅，具体的输出结果省略，主要的结论如下：其一，在一定样本容量一定分位点下，随着先验信息的增强，β0和β1抽样分布的标准差越来越小，而对估计均值的偏离误差没有明显影响，即增加先验信息可以提高参数估计量的精度。其二，0.5分位点下，β0和β1抽样分布的标准差均小于0.25和0.75分位点下的标准差，因此在采用Gibbs抽样算法进行贝叶斯分位数回归分析，尤其是预测时，在中位数下系数的预测精度更高。其三，在误差项服从正态分布的情形，一定样本容量一定分位点下，参数后验分布的标准差小于服从非对称拉普拉斯分布情形和误差项存在异方差下对应的标准差，这表明在贝叶斯分位数回归分析中，要求误差服从正态分布可以得到系数优良的统计性质。其四，在三种不同的先验分布下，β0和β1抽样分布的标准差均在0～2之间，尤其是在先验设定1下，先验的标准差为100，几乎是无信息先验的情形下，得到参数后验分布的标准差也不超过2，这也验证了已有的结论：贝叶斯分位数回归分析中即使先验分布是非合适的，得到的后验分布却是合适的[2，7]。

此外，还可以发现：无论设定哪种先验分布，β1的标准差总是小于同一分位点下β0的标准差，表明通过STAN软件得到解释变量系数估计值的统计性质要优于常数项估计值的统计性质，而且在各种先验分布设定下，随着样本容量增加，β0和β1的精度也随之提高。

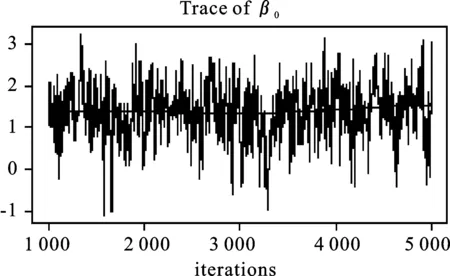
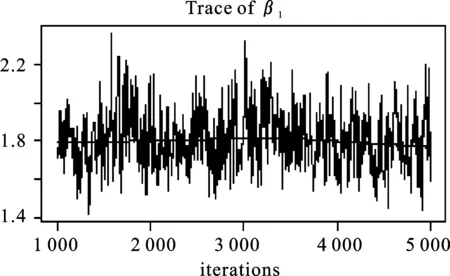
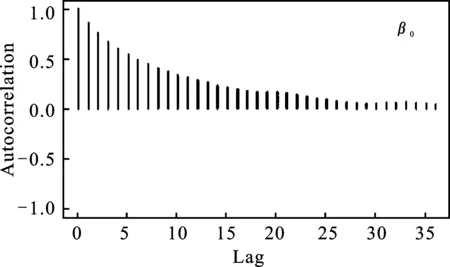
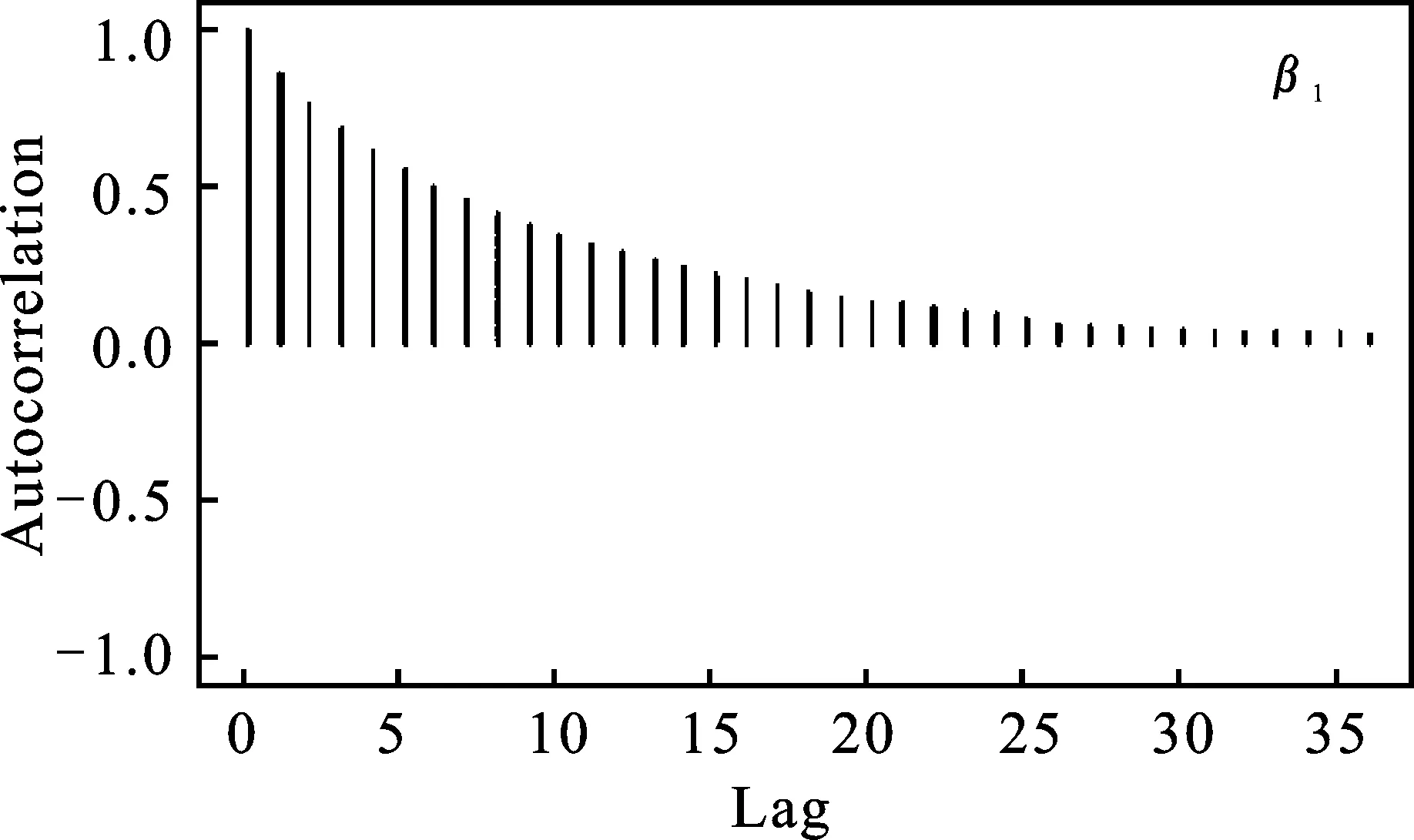
图3 β0和β1的抽样值轨迹和自相关图

综上，使用STAN软件采用HMC抽样算法进行贝叶斯分位数回归分析时，针对先验分布的选择问题，可以使用无信息先验，如果已经知道分位数回归系数为正态的情况下，就可以使用正态先验分布，而且可以考虑使用标准正态分布以提高参数估计量的精度；而先验分布的选择对于参数估计量的偏误没有显著影响。

五、结束语

本文在STAN中编译非对称拉普拉斯分布的似然函数，并在此基础上实现了贝叶斯分位数回归参数在STAN软件中的模拟抽样。同时，将尺度参数进行参数化，通过HMC抽样算法得到其后验分布。实验结果表明，与未参数化时相比，参数化后得到的估计量统计性质更好。在贝叶斯分析中，设定不同的先验分布意味着不同的主观信念，这种不同的信念最终会体现在参数的后验密度中，从而对估计结果产生影响。因此，本文针对连续因变量的贝叶斯分位数回归估计方法，模拟不同先验分布设定对参数估计量统计性质的影响。实验结果表明，合适的先验分布可以提高HMC抽样估计量的统计性质。

分位数回归和贝叶斯分析方法作为计量经济学的两大前沿分支，通过设定模型误差项服从非对称拉普拉斯分布而巧妙地结合起来，实现了对分位数回归模型的贝叶斯参数估计。本文仅探究了贝叶斯方法在分位数回归中的某些优越性，随着研究的深入，未来对贝叶斯分位数估计方法的探索将越来越广泛。

感谢波士顿学院肖志杰教授对本文的有益指导；感谢上海社会科学院研究生陈柯和王浩宇在软件方面的协助。文责自负。

[1] Fatti L P，Senaoana E M.Bayesian Updating in Reference Centile Charts[J].Journal of the Royal Statistical Society，1998，161(1).

[2] Yu K，Moyeed R A.Bayesian Quantile Regression[J].Statistics and Probability Letters，2001，54(4).

[3] Koenker R，Bassett G S.Regression Quantiles[J].Econometrica，1978，46(1).

[4] Yu Keming，Philippe van Kerm，Jin Zhang.Bayesian Quantile Regression：An Application to the Wage Distribution in 1990s Britain[J].The Indian Journal of Statistics，2005(5).

[5] Alhamzawi R，Yu K.Power Prior Elicitation in Bayesian Quantile Regression[J].Journal of Probability and Statistics，2011(2).

[6] Benoit D F，Van den Poel D.Binary Quantile Regression：A Bayesian Approach Based on the Asymmetric Laplace Distribution[J].Journal of Applied Econometrics，2012，27(7).

[7] 王新宇，宋学锋．基于贝叶斯分位数回归的市场风险测度模型与应用[J].系统管理学报，2009，18(1).

[8] 白仲林，隋雯霞，刘传文.混合贝塔分布随机波动模型及其贝叶斯分析[J].统计与信息论坛，2013，32(4).

[9] Linzer D.Dynamic Bayesian Forecasting of Presidential Elections in the States[J].Journal of the American Statistical Association，2013，108(501).