非线性项依赖于低阶导数的奇异分数阶弹性梁系统的可解性

刘兴元，杨梦云

(邵阳学院 理学院，湖南 邵阳，422000)

分数阶微分方程在物理、化学过程和工程建模中有着广泛的应用，近年来引起了人们极大的兴趣。许多学者在数学理论方面研究了分数阶微分方程，见文献[1-5，13]和其所引参考文献；对于分数阶微分方程的耦合系统的研究是其中重要的一个方面，因为这种系统广泛存在于各种实际问题中，参见文献[3，6-10]。据我们所知，对奇异弹性梁系统的可解性研究少有论文涉及，见文献[14-15]。

基于上述原因，我们讨论非线性项依赖于低阶导数奇异分数阶弹性梁方程的边值问题。

(1)

其中D0+是黎曼-刘维尔分数阶导数，f，g：(0，1)×R4→R是连续的，当t=0，t=1时，f，g可能是奇异的。

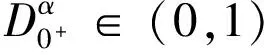
都满足方程(1)，则称偶合函数x，y是边值问题(1)的解。

我们利用巴拿赫空间的不动点定理，建立边值问题(1)的解的一些存在性结果。

1 预备结果

定义2.1 函数f：(0，)→R的α(>0)黎曼-刘维尔分数阶积分为

定义2.2 连续函数f：(0，)→R的α(>0)黎曼-刘维尔分数阶导数为

其中n-1<α≤n.

令

对u∈X，其范数定义为

易知X是实的巴拿赫空间。

令

对v∈Y，其范数定义为

易知Y是实的巴拿赫空间。

因此(X×Y，‖·‖)是由范数‖(x，y)‖=max{‖x‖=‖x‖X，‖y‖=‖y‖Y}，x∈X，y∈Y定义的实的巴拿赫空间。

引理2.1 假设

(B0)h∈C0(0，1)，存在M>0，k>-1，σ≤0使得2+σ+k>0，对t∈(0，1)，

|h(t)|≤Mtk(1-t)σ，

则对x∈X，当且仅当x满足

时，x是下列边值问题的解

(2)

证明方法可参考文献[2，5，12]。

引理2.2假设(B0)成立，则对y∈Y，当且仅当y满足

时，y是下列边值问题的解

(3)

证明方法与引理2.1相似。

在X×Y上定义算子T，对 (x，y)∈X×Y，T(x，y)(t)=((T1y)(t)，(T2x)(t))

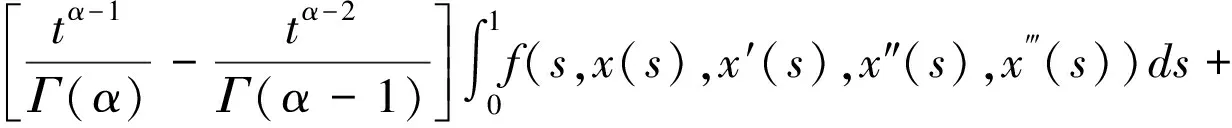
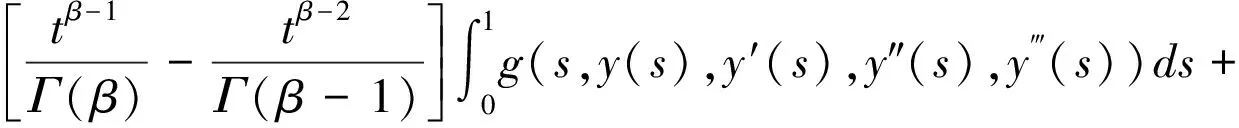
由引理2.1，引理2.2知(x，y)∈X×Y是边值问题(1)的解，当且仅当(x，y)∈X×Y是算子T的固定点。

引理2.3 假设

(B1)f(t，x，y，z，w)在(0，1)×R4上是连续的，且对每个r>0存在Mr>0，k1>-1，σ1≤0使得2+σ1+k1>0，且对t∈(0，1)，|x|，|y|，|z|，|w|≤r，

|f(t，tβ-2x，tβ-3y，tβ-4z，tβ-5w)|≤Mrtk1(1-t)σ1

成立，则算子T1：Y→X是全连续算子。

证明略。具体详细证明过程可参考文献[11，13]。

引理2.4 假设

(B2)g(t，x，y，z，w)在(0，1)×R4是连续，且对每个r>0存在Nr>0，k2>-1，σ2≤0使得2+σ2+k2>0，且对t∈(0，1)，|x|，|y|，|z|，|w|≤r，

|g(t，tα-2x，tα-3y，tα-4z，tα-5w)|≤Nrtk2(1-t)σ2

成立，则算子T2：X→Y是全连续算子。证明类似于引理2.3。

若(B1)(B2)成立，由引理2.3和引理2.4可知，T：X×Y→X×Y是全连续算子。

2 主要结果

定理3.1 假设

(B3)ψ∈C0(0，1)存在c0>-1，d0≤0使2+c0+d0>0和N0>0，对t∈(0，1)使得|ψ(t)|≤N0tc0(1-t)d0成立。

(B4)φ∈C0(0，1)存在a0>-1，b0≤0使2+a0+b0>0和M0>0，对t∈(0，1)使得|φ(t)|≤M0ta0(1-t)b0成立。

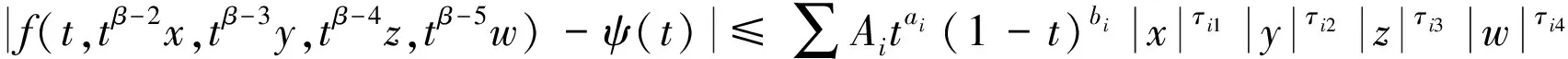
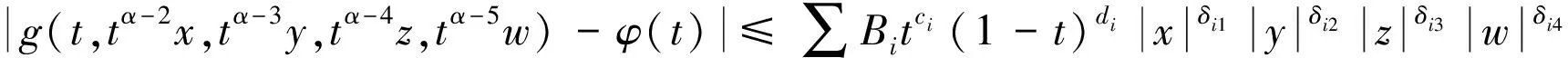
令

τi=τi1+τi2+τi3+τi4(i=1，2，…，m)，τ=max{τi(i=1，2，…，m)}，

δi=δi1+δi2+δi3+δi4(i=1，2，…，m)，δ=max{δi(i=1，2，…，m)}，

Ξi=max{Pi，Qi，Ri，Wi}

若当(i)τδ<1

(iii)τδ>1，

边值问题(1)至少有一个正解。

证明 显然(B5)和(B6)表明(B1)和(B2)成立，巴拿赫空间X×Y和定义在其上的算子T如前所定义，由引理2.3与引理2.4知T：X×Y→X×Y是全连续算子，(x，y)∈X×Y是边值问题的解，当且仅当(x，y)∈X×Y是算子T的固定点。

由(B3)和(B4)和引理2.1与引理2.2可以看出，Ψ∈Y，Φ∈X，。通过直接计算，我们得到

Ψ‴

Φ‴

对r1，r2>0，记

Ωr1，r2={(x，y)∈(X×Y)：‖y-Ψ‖≤r2，‖x-Φ‖≤r1}.

对(x，y)∈Ωr1，r2有

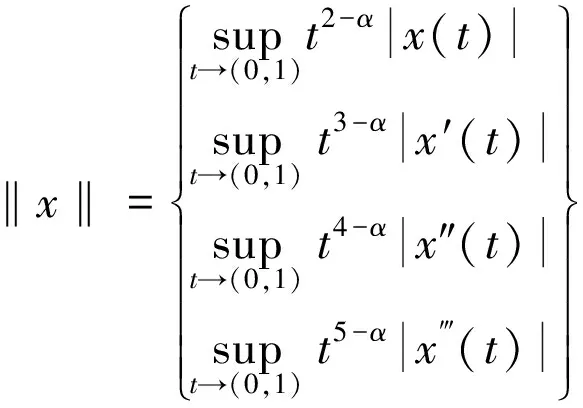
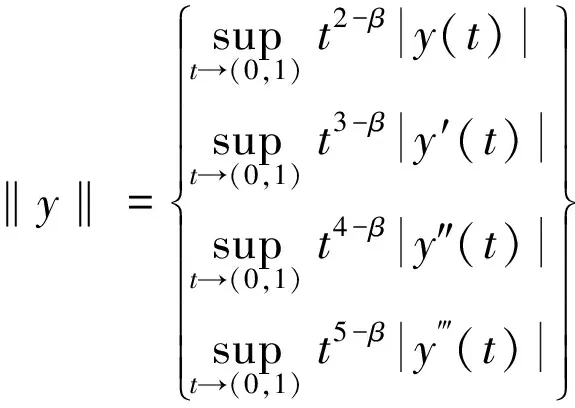
因此，对(x，y)∈Ωr1，r2有

|f(t，y(t)，y′(t)，y″(t)，y‴(t)-ψ(t)|=

|f(t，tβ-2t2-βy(t)，tβ-3t3-βy′(t)，tβ-4t4-βy″(t)，tβ-5t5-βy‴(t))-ψ(t)|≤

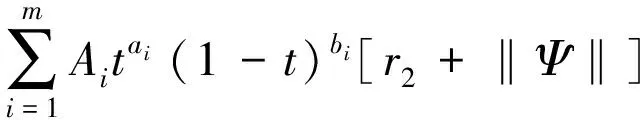
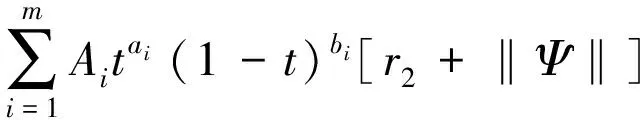
同理有

首先，我们容易推得

因此

(4)

另一方面

t2-α|(T1y)′(t)-Φ′(t)|≤

所以

(5)

类似地有

(6)

(7)

由(4)—(7)可以得到

(8)

类似地有

(9)

适当选取r1，r2使得

即

(i)当τδ<1时，存在足够大的r1>0使得

选取

故

Ωr1，r2={(x，y)∈(X×Y)：‖y-Ψ‖≤r2，‖x-Φ‖≤r1}.通过上述讨论有

因此T(x，y)∈Ωr1，r2由Schauder不动点定理，T至少有一个不动点(x，y)∈Ωr1，r2则(x，y)是边值问题(1)的一个解。

(ii)当τδ=1时，由于

存在足够大的r1>0使得

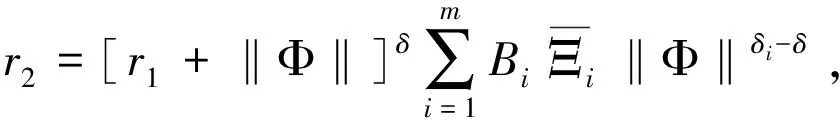
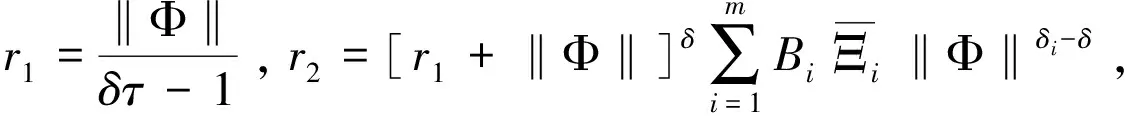
[1]SAMKO S G，KILBAS A A，MARICHEV O I.Fractional Integral and Derivative：Theory and Applications[M].Yverdon:Gordon and Breach Science Publishers，1993.

[2]AGRWAL R P，LIU Y，O′REGAN D，et al.Positive solutions of two-point boundary value problems for fractional singular differential equations[J].Differential Equations，2012，48(05)：619-629.

[3]AHMAD B，ALSAEDI A.Existence and uniqueness of solutions for coupled systems of higher-order nonlinear fractional differential equations[J].Fixed Point Theory & Applications，2010，2010(01)：1-17.

[4]AHMAD B，NIETO JJ.Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions[J].Computers & Mathematics with Applications，2009，58(09)：1838-1843.

[5]BAI Z.On positive solutions of a nonlocal fractional boundary valu problem[J].Nonlinear Analysis Theory Methods & Applications，2010，72(02)：916-924.

[6]GAFIYCHUK V，DATSKO B，MELESHKO V，et al.Analysis of the solutions of coupled nonlinear fractional reaction-duffusion equations[J].Chaos，Solitons and Fractals，2009，41：1095-1104.

[7]GEJJI V D.positive solutions of a system of non-autonomous fractional differential equations[J].Journal of Mathematical Analysis & Applications，2005，302(01)：56-64.

[8]GOODRICH C.S.Existence of a positive solution to systems of differential equations of fractional order[J].Computers & Mathematics with Applications，2011，62(03)：1251-1268.

[9]GUPTA C P.Existence and uniqueness theorems for the bending of an elastic beam equation[J].Applicable Analysis，1988，26(04)：289-304.

[10]KAUFMANN E R，KOSMATOV N.Elastic beam problem with higher order derivatives[J].Nonlinear Analysis Real World Applications，2007，8(03)：811-821.

[11]LU H，SUN L，SUN J.Existence of positive solutions to a non-positive elastic beam equation with both ends fixed[J].Boundary Value Problems，2012，2012(01)：1-10.

[12]YAO Q L.Positive solutions for eigenvalue problems of fourth-order elastic beam equations[J].Applied Mathematics Letters，2004，17(02)：237-243.

[13]ZHANG S Q.Positive solution of singular boundary value problem for nonlinear fractional differential equation with nonlinearity that changes sign[J].Positivity，2012，16(01)：177-193.

[14]LIU Y.Existence of positive solutions of fractional‐order elastic beam equation with a non-Carathéodory nonlinearity[J].Mathematical Methods in the Applied Sciences，2016，39(06)：1311-1324.

[15]LIU Y.On piecewise continuous solutions of higher order impulsive fractional differential equations and applications[J].Applied Mathematics and Computation，2016，(287-288)：38-49.