2017年高考浙江卷理科21题的探究与拓展*

北京市第十二中学高中部(100071)刘刚 赵毅

1.试题

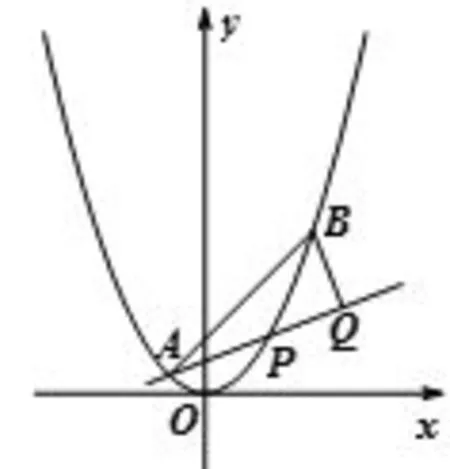
图1

(1)求直线AP斜率的取值范围;

(2)求|PA|·|PQ|的最大值.

试题考查了抛物线的方程、直线与抛物线的位置关系、斜率范围以及线段最值问题,考查了方程、转化与化归等数学思想以及坐标法的应用,检验了运算求解、分析问题与解决问题的能力.试题(2)问解法多样,为不同学生搭建了施展才能的舞台,是一道好题.

2.解法探究

点评解法1先表示出直线AP,BQ的方程,然后联立得到点Q的坐标,借助弦长公式表示出|PA|,|PQ|,最后通过导数工具求最值.

解法2 连接BP,则

点评解法2把|PA|·|PQ|转化为向量的数量积,然后坐标化,借助导数求最值,体现了向量的工具性作用,同时减少了运算量.

解法3 如图2,取AB的中点为C,以C为圆心,CB为半径作圆,因为AQ⊥BQ,所以点Q在圆C上.作直线PC与圆C交于D,E,由相交弦定理,得|PA|·|PQ|=|PD|·|PE|=(|CD|+|CP|)· (|CE|-|CP|).

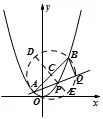
图2

点评解法3先挖掘图形特点,通过构造圆,把求|PA|·|PQ|的最大值转化为求|CP|的最小值,然后进一步得到以C为圆心,CP为半径的圆与抛物线x2=y在点P处有相同的切线时|CP|最小,从而使问题得以解决.解法体现了先几何后代数的特点,这是解决解析几何问题的一种常用思路.

以上三种解法各具特色,解法1是通解通法,但运算量大;解法3从几何图形入手,过程简洁,但不易被大多数同学想到;解法2借助向量知识,好想不难算,是解答本题最好的方法.向量是解决解析几何中有关平行(共线)、垂直、夹角、轨迹等问题的有力工具,借助向量知识,将几何问题坐标化、符号化、数量化,往往有出其不意、事半功倍之效,下面举例说明.

3.拓展

(1)解决共线问题.

例2 (2015年高考北京文科第20题)已知椭圆C:x2+3y2=3,过点D(1,0)且不过点E(2,1)的直线与椭圆C交于A,B两点,直线AE与直线x=3交于点M.

(1)求椭圆C的离心率;

(2)若AB垂直于x轴,求直线BM的斜率;

(3)试判断直线BM与直线DE的位置关系,并说明理由.

解(1)略,(2)略,1.

(3)直线BM与直线DE平行,解答如下:

当直线AB与x轴垂直时,经过验证BM//DE.

而

(3)处理轨迹问题.

例4 如图3,O是直角坐标原点,A,B是抛物线y2=2px(p＞0)上异于顶点的两动点,且OA⊥OB,OM⊥AB并与AB相交于点M,求点M的轨迹方程.

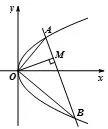
图3

4.练习

练习1 (2017年全国高中数学联赛新疆初赛)已知椭圆的离心率为椭圆短轴的上下两个端点分别为A,B.以A为圆心,椭圆长半轴长为半径的圆与椭圆交于C,D两点,CD的中点的纵坐标为

(1)求椭圆的方程;

(2)直线l过椭圆的右焦点F且不垂直于x轴,l与椭圆交于M,N两点,设点N关于x轴的对称点为N′,问直线MN′是否经过定点?若经过定点,求出这个定点;否则,说明理由.答案:(1)椭圆的方程为直线MN′经过定点(4,0).

练习2 (2015年高考安徽文科第20题)设椭圆E的方程为点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足|BM|=2|MA|,直线OM的斜率为

(1)求E的离心率e;

(2)设点C的坐标为(0,-b),N为线段AC的中点,证明MN⊥AB.答案:(1)(2)略.

练习3 (2016年全国高中数学联合竞赛湖北省预赛)过抛物线y2=2px(p＞0)外一点P向抛物线作两条切线,切点为M、N,F为抛物线的焦点.证明

(1)|PF|2=|MF|·|NF|;

(2)∠PMF=∠FPN.答案:略.