改进的自适应特征细分方法及其对Catmull-Clark曲面的实时绘制
林金花,王延杰,孙宏海
(1.长春工业大学 应用技术学院,长春130012;2.中国科学院长春光学精密机械与物理研究所 机械电子工程系,长春130033;3.中国科学院大学 大衍学院,长春130033)
0 引 言
细分曲面自诞生以来已被广泛应用于三维虚拟现实领域[1-4]。由于细分规则的计算方法较简单,使得细分曲面表示方法的兼容性大大提高。尽管如此,细分表面点的计算需要耗费大量的时间和空间性能,限制了细分曲面技术的使用范围。通用编程图形处理芯片(GPGPU)的出现拓宽了细分曲面技术的使用范围,这种参数化方法提高了细分绘制效率,但是当曲面结构复杂且曲面片规模较大的情况下,GPGPU的工作性能也随之受到影响。Niessner等[5]于2012年提出了一种新的网格细分技术,从软件方面克服了GPGPU的缺陷,直接GPU芯片上进行计算分析操作。然而这种方法以参数曲面的表示精度作为代价,绘制速度提高的同时,精度也随之下降。自适应细分方法(FAS)的出现改变了现状,仅对特征区域进行细分操作,既提高了细分性能,又保证了复杂曲面的绘制精度。FAS广泛应用在三维动画软件和游戏制作领域,例如:OpenSubdiv,一种由皮克斯动画工作室采纳的开源新方案。
与传统细分算法相比,FAS仅对不规则区域进行细分,不仅保留了不规则区域的拓扑特征,还提高了细分速度。然而,当不规则区域的数量大规模增加时,FAS算法的效率会随指数降低,限制了算法的时间性能。
为了改善FAS方法的实时绘制速度,本文对FAS方法进行了改进,提出了一种动态的自适应特征细分算法,通过构造特征块处理单元来动态地提取和细分不规则块,实现不规则区域的不同细分深度的划分,得到较少数量的细分块,减少渲染块的数量,提高绘制速度。此外,本文使用块缓冲区来并行地处理所有细分层次产生的块,提高了细分速度。
1 相关概念和理论
1.1 可编程图形处理器
GPU是一种单指令流多数据流模式的并行图形处理器。本文细分管线使用GPU绘制流程,对GPU进行编程,增加了两个功能模块:可编程顶点处理器和可编程块处理器,如图1所示。

图1 可编程图形流水线Fig.1 GPU rendering pipeline
GPU处理芯片仅对表面点操作,对于上级细分顶点的控制能力较弱。块处理器弥补这点不足,直接在块级上对几何曲面进行计算和光栅化处理,从而可以充分地表现多边形内部细节。
块处理器负责执行处理块参数值的程序,对通过流水线的每一个块都执行一遍。顶点处理器的输出缓冲区中的顶点参数经过插值后,生成块参数传递给块处理器的输入缓冲区,作为其输入参数。程序执行后,改变后的块参数被写入到块处理器的输出缓冲区中。本文算法的细分核心部分就是在块处理器上实现的。
1.2 Catmull-Clark细分规则
Catmull-Clark细分模式[6]是一种传统的细分曲面生成方法,通过网格计算规则来重复递增地生成双三次B样条参数曲面。本文使用Catmull-Clark细分来初始化特征曲面片。Catmull-Clark细分模式如下所示:
(1)面点:每个面的4个顶点记为V1、V2、V3、V4,面点计算规则(见图2(a))如下:

(2)边点:首先将内部顶点记为V i、V j,此顶点的邻接面分别记为F1和F2,边点计算规则(见图2(b))如下:

(3)顶点点:点V的邻接点分为记为V1,V2,…,V2N,顶点点的计算规则(如图2(c))如下:

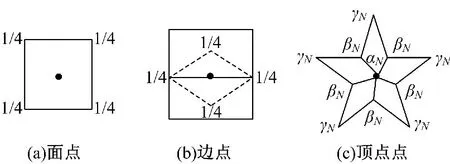
图2 Catmull-Clark细分规则Fig.2 Catmull-Clark subdivision rule
1.3 自适应特征细分(FAS)算法
FAS算法是Niessner等[7,8]提出的一种基于GPU的快速曲面绘制方法。该算法包括初始化阶段、细分核心部分和分层绘制3个部分。各部分功能详述如下:
(1)初始化阶段。对初始曲面进行分析,定义自适应特征部分,抽取特征块,生成块内控制顶点集合。同时进入索引缓冲单元,用于存放数据,索引缓冲单元主要由信息块和索引表构成。依据Catmull-Clark细分模式,得出每个层次的细分点的信息,同时存储到细分表中,即:面点表、边点表和顶点点表。
不同细分层次下的表面拓扑呈现出不同的网格连接结构,为了实现不同细分层次间曲面片的链接,FAS使用转换块来实现,转换块由5种模板组成,分别对应不同细分层级间的表面结构,连接后的表面拓扑结构完整且无缝,如图3所示。

图3 FAS转换块模板Fig.3 FAS join_patch model
(2)细分核心部分。依据细分模板和细分初始网格模型,对不规则区域细分到各自不同的细分深度,得到曲面的关键控制顶点。再根据细分表中的内容,计算得出下级细分层次上的顶点数据,将其存储到GPU缓存。每个不规则区域的细分层级是固定不变的。
(3)分层绘制。将前两个部分得到的细分结果和表面模型数据作为本阶段的输入,经过细分后的表面模型,将其存放到对应的GPU存储单元中。GPU处理器将存储单元中的待细分数据完成细分操作,得到顶点和表面拓扑数据,并将其送入渲染器完成整体模型的绘制过程。
由此可见,FAS对网格模型的全部细分块使用统一的细分深度,通常会出现GPU缓冲不够或运行缓慢的现象。本文算法对FAS算法中的不规则区域设置了不同的细分深度,对于距离视点较远且分辨率较低的区域使用较低的细分层级,简化了细分计算,保证了模型绘制分辨率,同时提高了GPU绘制速度。
2 改进的算法架构
2.1 改进的数据结构
本文对传统FAS算法的数据结构进行了扩充,如下所示:
(1)细分表结构
本文对FAS的细分表结构进行了改进,如图4所示,不同的颜色线圈代表不同细分层级下的网络点,这些网格点的位置信息存放在细分表中,同时为了保证GPU快速读取这些顶点信息,本文将生成的二维表存放在GPU缓冲中,以便随时读入GPU绘制区域完成实时绘制。
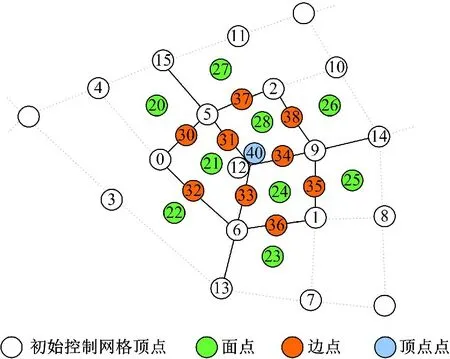
图4 特征图(细分深度为3)Fig.4 Feature mapping(subdivision depth 3)
首先,使用Catmull-Clark模板生成曲面模型,存储为面点表、边点表和顶点点表,主要存放顶点和前一级别的关键点。其次,为所有的坐标点分配各自的编码,构成细分表中的二元信息数据。最后,对GPU全局缓存进行实时更新操作,关键点被存入GPU的细分表。
改进的细分表结构如图5所示[9]。与FAS的区别在于本文仅仅对GPU缓存中存放的少数关键点进行更新操作,并将其存储在细分表中,节省了GPU的计算时间,同时减少了存储单元的占用数量。

图5 扩充的细分表Fig.5 Extended subdivision mapping
(2)渲染表

图6 渲染块(dv=3)Fig.6 Rendering patch(depth=3)
本文将待渲染的数据存放在渲染表中,主要包括奇异点周围块的细分层次dv、邻接块的拓扑信息和邻接顶点的属性值,FPU接收渲染表中数据,再送入GPU处理单元进行渲染处理,如图6所示。换块被分成3个三角形区域,不同的细分深、转换块具有不同的拓扑缩放,当达到细分因子规定的深度后,不规则区域的自适应细分结束,表示奇异点周围的不规则区的拓扑结构已经到达最逼近真实渲染效果的程度,此时停止细分,将渲染表送入GPU,GPU开始对渲染表中的数据进行渲染绘制。图7为渲染块表缓冲区。
渲染表中的块属性包括特征块、规则块和不规则块。特征块通常可用于连接周围块的拓扑信息,即作为转换块出现;规则块是无需细分的块;而不规则块是本文自适应细分的对象,即要经过不同层级的细分,实现对奇异点区域的细分绘制。如图6所示,红色顶点表示奇异点,第3幅图表示奇异点周围块已被细分3次,而不同细分层次间使用绿色的转换块实现块间的无缝拼接,每个转

图7 渲染块表缓冲区(dv=3)Fig.7 Rendering patch table buffer(depth=3)
2.2 细分因子
本文对FAS的细分因子进行了扩充,生成不规则块的细分层次,进而控制奇异点周围的不规则区域的自适应细分过程,下面依据不同的块属性,将细分因子生成方式进行了划分:
(1)规则块:使用GPU内部设置的细分层级。
(2)不规则块:当不规则区域由n个顶点构成时,P={p1,p2,…,t,…,p n},t表示奇异点,P对应的特征图表示为V(P)。k表示初始模型中不规则块的顶点,P′=k∪{P},将P′所对应的特征图表示为V(P′)。当V(P′)包含t所属的块,即奇异点所属特征块与k所属于特征块之间的最小距离值与真实值相差α时,P的细分因子计算公式如下:

式中:V(t)为t所属的特征块的最短距离函数;Area()为特征块的面积值;,e表示周围邻居边,m表示周围边的数量;表示特征块的三维变化矩阵,如图8所示[10,11]。

图8 特征单元变换过程Fig.8 Feature unit space transformation
2.3 动态自适应特征细分

图9 本文算法框图Fig.9 Block diagram of proposed algorithm
本文算法通过对每个不规则块单独分配不同的细分深度来实现动态细分过程,进而减少细分产生的计算量。算法流程图如图9所示,包含3个模块:①FPU-特征块处理单元,用于计算块的细分层次,并构建细分表;②由Catmall-Clark细分模板,对曲面进行细分,生成关键点;③使用GPU绘制渲染表中的不同属性的块。
第一阶段:特征块处理单元。由式(1)得到细分因子的确切值,对GPU的处理单元进行编码,自动生成不同特征块的各自细分层次。由初始网格模型计算得到的控制顶点数量作为输入数据的索引信息传送给FPU,FPU经过本文算法管线后得到3张表,分别为细分层次表、细分表和块渲染表,执行FPU的关键代码,如下所示:

本文的FPU计算得到细分表,该细分表用于存储即将进入GPU的细分顶点,同时存放这些顶点的特征图,依据不同的顶点输入将细分表分层3个表结构:面点区、边点区和顶点点区,如图5所示。FPU同时构建渲染表,依据渲染块的类型将其分为3个表:规则表、不规则表和转换表。FPU依据细分表生成的细分深度l、块的细分因子t和GPU缓冲信息绘制索引缓冲区的内容。
第二阶段:细分。算法首先对初始网格进行全局扫描,计算得到全部需要细分的区域,然后使用Catmull-Clark细分模板和GPU块处理单元对这些细分数据进行处理,得到每个细分层级上的顶点信息。本文算法对不规则区域周围的奇异点进行自适应细分,得到不同拓扑结构的网络表面数据,并将这些数据传输给GPU进行二次绘制渲染。
第三阶段:块绘制。使用改进的细分因子计算方法得到不同细分层次上的深度数据,实现对不规则区域的自适应细分。而对于规则块和细分块,本文采用FPU渲染管线来处理。GPU根据渲染表和细分表中的数据,对处理单元中的信息进行并行的光栅化操作,渲染输出所有细分后生成的块数据,实现对不规则区域的实时细分,提高块的绘制精度[12,13]。
3 实验分析
3.1 实验的软件与硬件环境
操作系统为Windows 8,开发语言为C++,开发工具为Microsoft Visual C++6.0,采用高级绘制语言,三维图形编程接口Direct3D。CPU类型/主频为INTEL Xeon E5/3.0 GHz,内存为8 Gbit。采用图形处理器NVIDIA GTX 980,该图形处理器有11条像素管线,支持OpenGL4.4/Direct X12。
3.2 性能分析
3.2.1 精确性(显示精度)比较
建立初始控制网格(见图10(a)),控制网格由四边形网格组成,具有明显折痕和尖点等不规则特性。图10(b)为采用经典FAS方法对初始控制网格细分绘制之后的效果图,图10(c)为采用本文算法对初始控制网格绘制之后的效果图。图10(d)、(e)、(f)分别是对前3个效果图取一个不规则区域(河马背上的小鸟)放大之后的效果图。由图10(e)、(f)的局部放大效果图可以看出,本文算法显示精确性与FAS方法相近,无法用肉眼辨别出不同。传统FAS方法使用相同的细分层次对表面模型的不规则区域进行细分,渲染输出的精度较高,存在的弊端是对应每个块计算相同的细分深度会增加GPU的计算时间,本文算法通过对经典FAS算法进行扩充,对奇异点周围的不规则区域进行了不同层次的细分,能够较完整地构建曲面模型的表面拓扑结构,同时降低了块的细分和渲染时间,GPU的渲染精度也更加逼真。

图10 本文算法与经典FAS算法的比较Fig.10 Proposed method compared with classical method
由图10(e)、(f)的局部放大效果图可以看出,本文算法显示精确性与FAS方法相近,无法用肉眼辨别出不同。经典的FAS算法对初始控制网格的不规则块使用统一的细分深度,绘制效果好,但块计算量较大,本文算法通过对经典FAS算法进行扩充,对不同区域的不规则块使用不同的细分深度,较好地保留了曲面模型的折痕等局部特征,块计算量较小,绘制效果逼真。
3.2.2 实时性(绘制速度)比较
分别采用FAS算法和本文算法对图11中的模型进行细分绘制绘制,并根据不规则块的数量不同来比较两种算法的绘制速度和细分速度,如表1所示。

图11 复杂度不同的3种模型初始控制网格Fig.11 Primitive grid of three different models

表1 两种算法绘制曲面模型速度的对比Table 1 Speed comparison of two algorithm with different models
分析表1中数据可以得出如下结论:
(1)与FAS方法不同,本文算法的细分阶段包含了FPU的执行时间,尽管如此,本文算法的细分速度仍比FAS算法快。
(2)选取4个具有不同复杂程度的初始网格模型,计算FAS算法与本文算法的速度差,曲面模型包含不规则块或点越多,本文算法绘制细分曲面模型的速度越快。
3.2.3 绘制性能比较
采用本文算法与FAS算法在大规模地形场景上进行绘制性能比较,模型的四边形面片数量为805 293个(见图12)。在较密集特征块下绘制同一种模型,本文算法绘制速度较快,即当细分密度越是增大时,本文算法绘制速度增快越明显。图13给出了两种算法绘制该场景所需的总体绘制时间比较。本文算法能够在场景网格上产生均匀的细分密度,适用于大规模场景的实时绘制。

图12 本文算法对大规模地形场景的绘制Fig.12 Proposed algorithm applied to the rendering of large-scale terrain scene

图13 两种算法绘制大规模场景模型时间对比Fig.13 Time comparison of two algorithms for rendering large-scale scene
4 结束语
提出了一种基于GPU的动态自适应特征细分方法,能够对表面特征较明显的三维Catmull-Clark细分曲面模型进行实时绘制,并且通过引入新的细分因子计算方法,构建特征块处理单元来改进FAS方法的过度细分问题。实验生成的三维曲面模型显示分辨率良好,绘制速度与传统FAS方法相比提高了28%,能够满足三维虚拟环境的实时绘制需求。本文方法还可以应用于其他虚拟环境中的三维曲面模型的建立,例如Loop曲面模型的动态自适应绘制,对于用一般方法难于模拟的具有多不规则表面特征的曲面模型有较好的绘制实时性。
[1]Niessner M,Loop C,Meyer M.Feature-adaptive GPU rendering of Catmull-Clark subdivision surfaces[J].ACM Transactions on Graphics,2012,31(1):1-11.
[2]Doo D,Sabin M.Behaviour of recursive division surface near extraordinary points[J].Computer-Aided Design,1978,10(6):356-360.
[3]Loop C,Schaefer S.Approximating Catmull-Clark subdivision surfaces with bicubic patches[J].ACM Transactions on Graphics,2008,27(1):1-11.
[4]Stam J.Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values[C]∥Proceedings of SIGGRAPH,New York,NY,USA,1998:395-404.
[5]Niessner M,Loop C,Greiner G.Efficient evaluation of semi-smooth creases in Catmull-Clark subdivision surfaces[C]∥Eurographics Proceedings,Cagliari,2012:41-44.
[6]Catmull E,Clark J.Recursively generated B-spline surfaces on arbitrary topological meshes[J].Computer-aided Design,1978,10(6):350-355.
[7]Niesser M,Loop C.Analytic displacement mapping using hardware tessellation[J].ACM Transactions on Graphics,2013,32(3):1-9.
[8]Schafer H,Niessner M,Keinert B.State of the art report on real-time rendering with hardware tessellation[C]∥Eurographics,Strasbourg,France,2014:93-117.
[9]黄韵岑,冯洁青.表驱动的细分曲面GPU绘制[J].计算机辅助设计与图形学学报,2014,26(10):1567-1575.Huang Yun-cen,Feng Jie-qing.Mapping driving subdivision surface upon GPU rendering[J].Journal of Computer-Aided Design&Computer Graphics,2014,26(10):1567-1575.
[10]Deng C,Ma W.A unified interpolatory subdivision scheme for quadrilateral meshes[J].ACM Transactions on Graphics,2013,32(3):1-10.
[11]李桂清.细分曲面造型及应用[D].北京:中国科学院计算技术研究所,2001.Li Gui-qing.The modeling and application method to subdivision surface[D].Beijing:Institute of Computer Technology,Chinese Academy of Sciences,2001.
[12]Schafer H,Keinert B,Niessner M.Local painting and deformation of meshes on the GPU[J].Computer Graphics Forum,2015,34(1):26-35.
[13]Yuan Ya-zhen,Wang Rui,Huang Jin.Simplified and tessellated mesh for realtime high quality rendering[J].Computer and Graphics,2016,54(10):135-144.

