α稳定分布特征指数估计算法

关济实,石要武,邱建文,单泽彪,史红伟

(1.吉林大学 通信工程学院,长春130022;2.中广核研究院有限公司 北京分公司 北京100083;3.长春理工大学 电子信息工程学院,130022)

0 引 言

一类带有冲击特性的非高斯噪声在大气、水下声学以及电磁干扰等噪声中大量存在,该类噪声表现出极强的脉冲特性,由于α稳定分布可以用来很好地描述这一类噪声[1-3],近年来α稳定分布噪声背景下的信号处理方法得到了广泛研究。在α噪声背景下的信号处理方法的研究中,分数低阶矩和共变被大量应用[4-6],而分数低阶矩和共变只有在α稳定分布噪声参数已知的情况下才有意义,所以大多研究都假设α噪声的参数已知,至少是其特征指数α已知。在实际应用中,由于没有α噪声的相关参数,导致这些算法的应用受到很大的限制,因此研究α稳定分布的参数估计方法对于以上这些算法的应用具有支撑作用。在α稳定分布参数估计方面,Tsihrintzis[7]、Ma等[8]基于分数低阶矩和负阶矩理论提出了多种通过观测序列估计α稳定参数的方法,Kuruoglu[9]借助混合高斯模型,提出了α稳定概率密度函数的一种新的表达式,并利用该表达式进行α稳定分布的参数估计。Du Mouchel[10]提出了一种最大似然估计方法,Brorsen等[11]对该方法进行蒙特卡罗仿真,获得了相当好的结果,然而,该方法属于高度的非线性优化问题,由于需要计算复杂的数值积分,计算量非常大。本文提出一种α稳定分布信号的α和γ参数估计的方法,该方法利用α的叠加性质,通过简单的运算即可实现对α估计,容易理解且计算量小,估计精度高。

1 α稳定分布的定义和性质

1.1 α稳定分布的定义

α稳定分布的概念是Levy在1925年研究广义中心极限定理时提出的[3],中心极限定理引出了高斯分布,而广义中心极限定理则是放开了中心极限定理中有限方差这一限制后形成的。α稳定分布是负责广义中心极限定理的一簇分布,高斯分布是α稳定分布在α＝2时的一个特例[12]。除了有限的几种情况,α稳定分布没有封闭的概率密度函数表达式[13],α稳定分布的定义是由其概率密度函数的傅里叶变换,即特征函数给出的。

定义 若一个随机变量X的特征函数可以表示为:

式中:－∞＜μ＜∞,γ＞0,0＜α≤2,－1≤β≤1,这4个参数决定了该分布的形状,sign(x)为符号函数。称该变量X服从α稳定分布,服从α稳定分布的噪声称为冲击噪声,脉冲噪声或稳定分布噪声,写作:

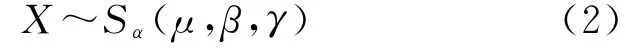
式中:α称为特征指数,它决定了脉冲特性的程度,α越小,脉冲程度越高;β称为对称系数,当β＜0时,信号的概率密度函数会出现左倾,反之出现右倾。当β＝0时,α稳定分布的概率密度函数呈现左右对称形状,称为对称α稳定分布(SαS);μ称为位置参数,表示α稳定分布概率密度函数的中心,也是α稳定分布变量的期望值;γ称为分散系数,在同一个α值下,γ越大,则概率密度函数的两侧延伸越严重,中间部分的值则会相对降低,与高斯噪声的方差类似。

1.2 α稳定分布的性质

现有文献对α稳定分布的性质做了详细的研究,本文不再一一说明,仅介绍本文算法相关的两条性质,即叠加性质和p范数性质[14]。

性质1 叠加性质,若X1～Sα(μ1,β1,γ1),X2～Sα(μ2,β2,γ2),则它们的和变量X＝X1＋X2服从X～Sα(μ,β,γ),其中:

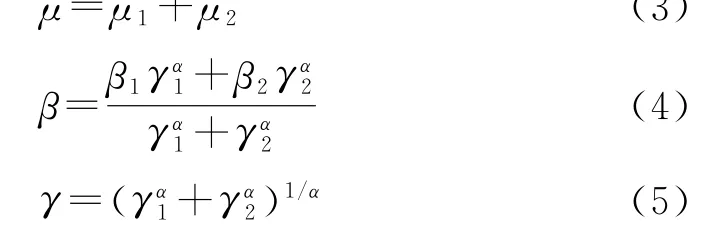
性质2 若X～Sα(u,β,γ),0＜α＜2且当α＝1时,有β＝0,则对于所有0＜p＜α,有:

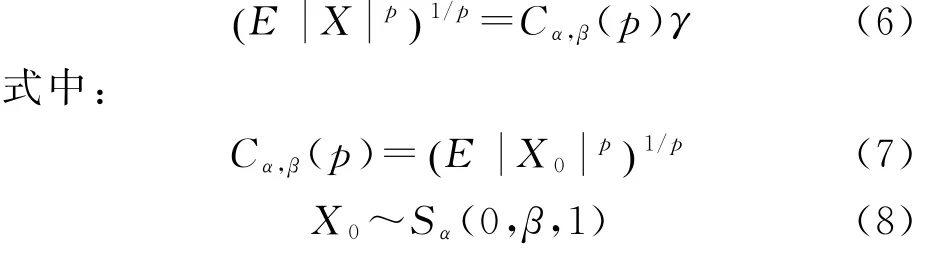
2 基于组合分布和分数低阶矩的系数估计方法

2.1 特征指数估计算法原理

根据α分布的性质1,两个独立的同特征指数的稳定分布变量相加时,其和变量同样服从α分布,并且其分散系数仍为α,当多个同分布的α信号相加时,这一性质可以以如下形式表述:

推理 当X1,X2,…,X N相互独立且均服从于同一分布Sα(μ,β,γ)分布时,其和分布X＝X1＋X2＋…＋X N服从Sα(μ0,β0,γ0),则其参数表达式为:

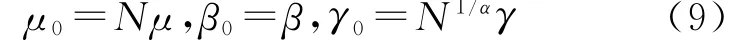
对照性质1,此推理很容易得证。

从以上推理中可以看到,多个独立同分布的α变量的和变量仍服从α分布,且其对称系数不变。注意到这一性质分散系数的表达式中并没有对称系数,所以分散系数的这一性质对于非对称α分布也是适用的。

综合以上两性质和推理,多个同分布变量相加时有:

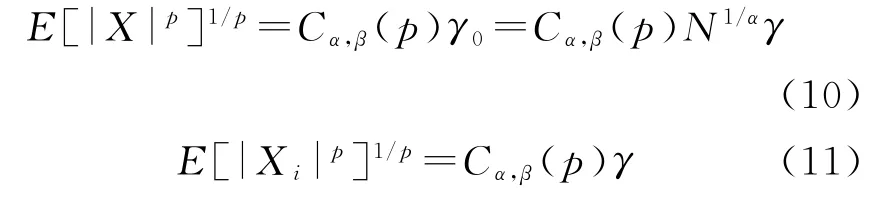
式中:i＝1,2,…,N。

和变量X与原变量X i的p阶矩之间具有以下关系:

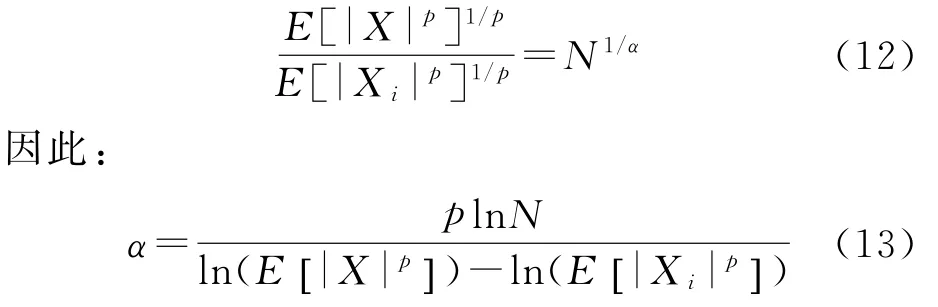
由式(13)可知,当有多个同分布α稳定分布随机变量时,可以将多个随机变量组合,利用组合变量与原变量之间p范数关系,得到特征指数α的估计。

2.2 α稳定分布参数估计方法

2.2.1 参数估计方法

式(13)表明多个同分布的α信号相加时,其统计量E[|X|p]1/p之间的比只与参与相加的变量个数和特征指数α有关。利用这一特征,可以从实际采样信号中估计得到特征指数α。

当一个变量的时间相关性很低时,相隔足够长时间以外的多个采样值之间可以认为是不相关的。对于一个α分布的变量,相隔足够长的时间进行多次采样,则可以认为多次采样结果为多个独立同分布的α分布变量,这多次采样相加,得到的新变量与原变量之间可以根据式(13)得到α的估计。对于一个足够长时间的采样序列X,该方法可以描述如下:

设有序列长度为L的α稳定分布变量采样序列X＝{x i,i＝1,2,…,L},将X等分为N＋1份,每份长度为K(K＝L/(N＋1)),则有:

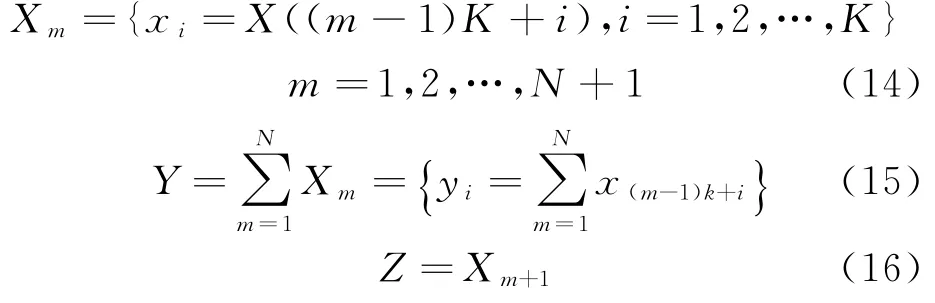
由以上定义可知,Y和Z是相互独立的随机变量。

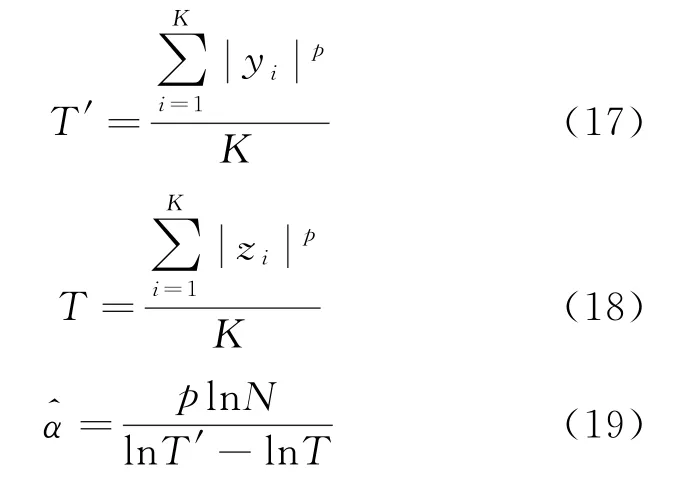
算法的执行步骤如下:

(1)对待测信号采样L次,形成X。

(2)将L次信号平均分割为N段,形成X m,m＝1,2,…,N。

(3)将分割的数据相加,形成X′。

(4)对X和X′分别计算统计量T和T′。

(5)将数据代入式(19)得到特征指数α的估计值。

该方法不需要复杂的计算,相比于现有的参数估计方法,计算量较小。并且不涉及α分布概率密度函数的封闭形式的近似,原理简单可靠,便于理解和编程实现。在实际执行时,由于α未知,为了使p阶矩收敛,可以使p尽量小。

2.2.2 估计方法的无偏性与一致性分析

式(12)由α稳定分布的性质导出,因此它是严格成立的,但在实际运算中,无法直接得到变量的p阶矩,只能以式(17)得到的估计,式(17)中统计量T′的数学期望为:

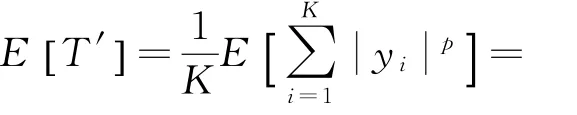
再来分析估计的一致性,定义变量D如下:

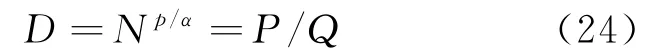
α与D之间是幂函数关系,二者之间是一一对应的,因此如果算法中对D的估计是无偏的,则对α的估计也将是无偏的,算法中D的估计值为:

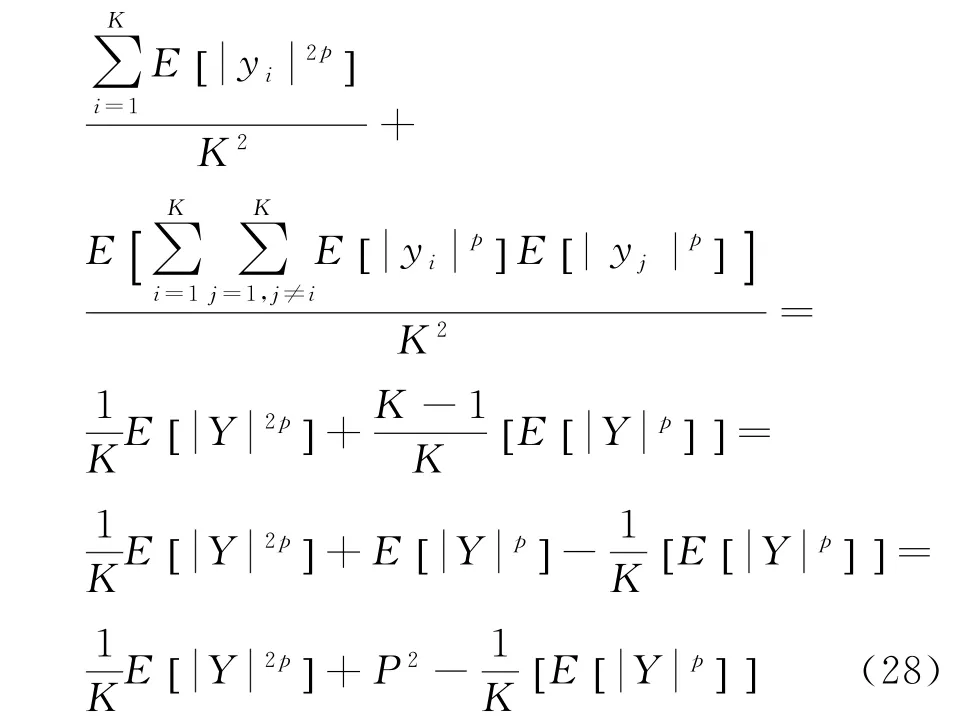
当2p＜α时,均为有限值,当采样长度无穷长,即L无穷大时,K＝L/N也趋于无穷大,因此式(28)可写作:

因此,当采样长度无穷大时,式(27)可表示为:

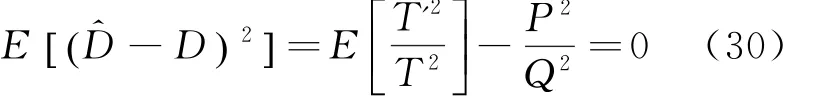
3 数值仿真实验

实验1 不同α值的特征指数估计实验

实验目的:验证算法的有效性。

实验方法:α的取值从0.1至2,每隔0.1取一个α值,利用数值方法实现β＝0,γ＝1,长度为10 000的α分布序列,分割为两段,通过式(19),取p＝0.1计算α的估计值,并与产生数据所用的α相比较,以验证算法的有效性。

估计结果与生成数据时所用α之间关系如图1所示。

从图1可以看到,该方法准确地估计了α的值。为考察算法精度,定义估计均方误差:

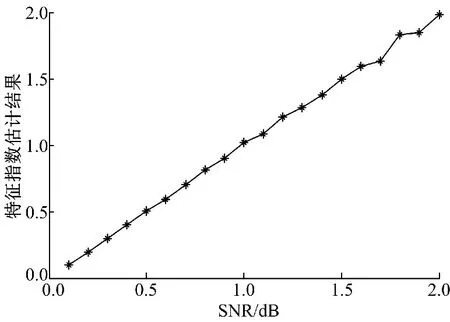
图1 基本的α估计实验结果Fig.1 Estimation result ofαwith basic experiment

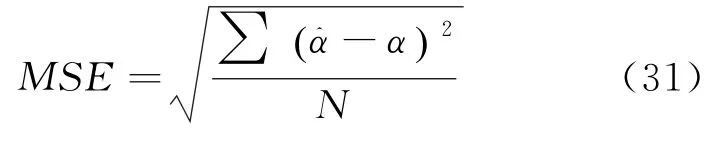
每个α取值进行100次蒙特卡罗实验,计算均方误差,图2为均方误差图。

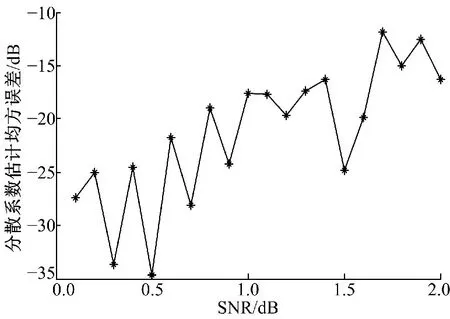
图2 α估计均方误差Fig.2 Estimation MSE ofαwith basic experiment

可以看到,随着α变大,均方误差逐渐变大,当α＝2时,均方误差仅为－12 dB,具有较高的估计精度。

实验2 分割段数对算法的影响

实验目的:验证分割段数对于算法精度的影响。

实验方法:特征指数取0.6,0.9,1.2,1.6,分段数分别取[2,3,4,5,6,8,10,12,15,16,20,24]进行计算,每种情况进行100次蒙特卡罗实验,为了得到完整的分段,实验数据长度取12 000,记录估计值和均方误差,观察分段数对于估计误差的影响。

图3为分段数变化时特征指数的估计结果和均方误差。

从图3可以看出,不同分段数时,本方法均可以有效估计α值。从均方误差结果图中可以看到,段数变大估计均方误差变大,这是由于分段数变大使得每段数据量变小,从而使得p范数的估计误差变大引起的。本方法对α的估计误差始终在－13 dB以下,估计精度较高。

实验3 分散系数对算法的影响实验

实验目的:验证不同分散系数γ时的算法性能。

实验方法:γ从0.1变到10,每隔0.1取一个点,α取0.6,0.9,1.2,1.6,进行4次实验,每种情况进行100次蒙特卡罗实验,分段数取4,每次实验数据长度为10 000,记录估计值和均方误差并形成曲线。

图4为γ分段数变化时估计误差结果。

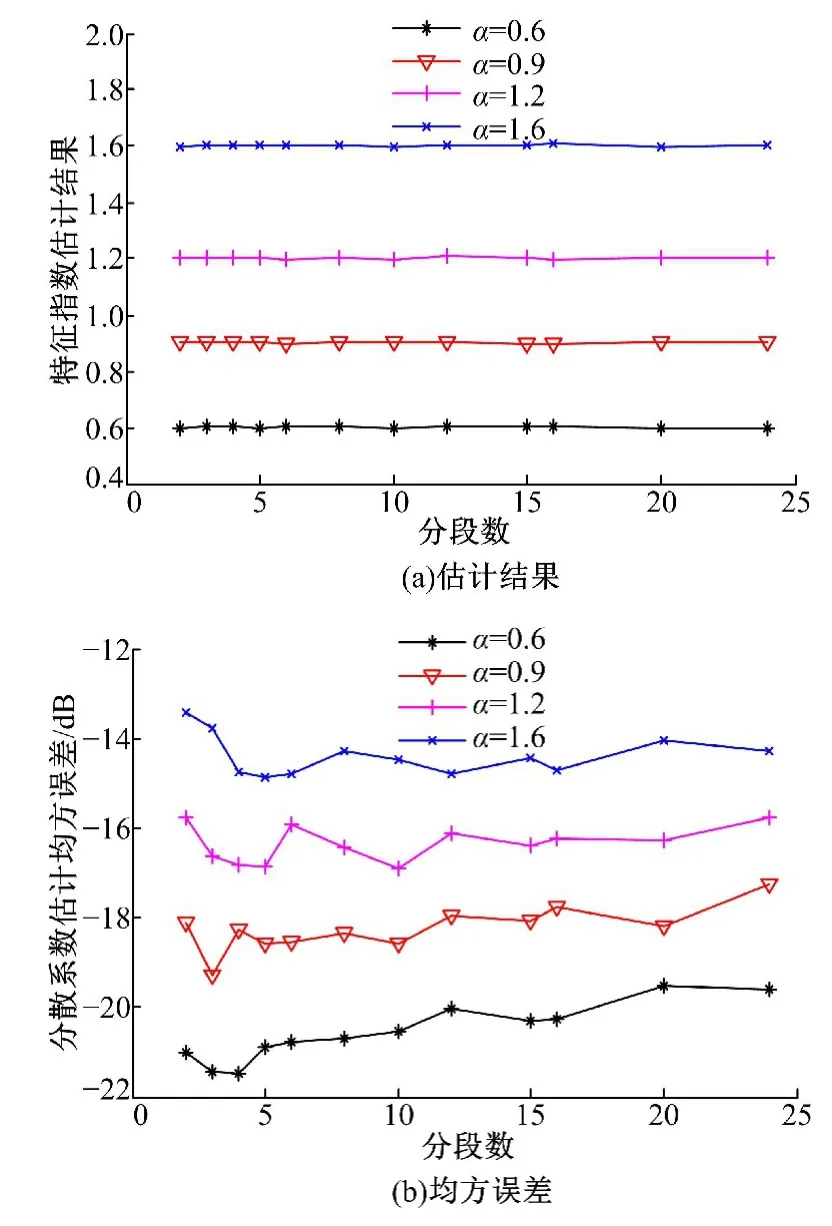
图3 分段数对α估计结果的影响Fig.3 Influence of section number on estimation ofα

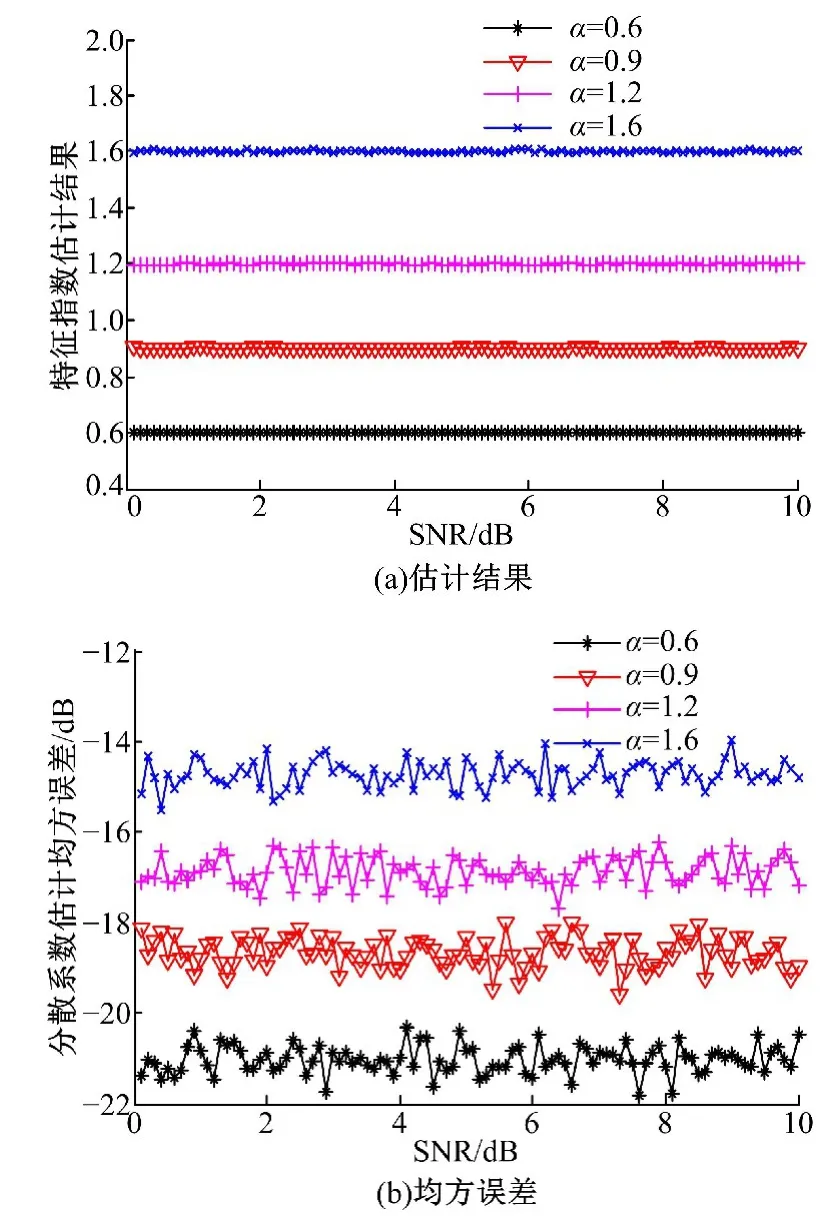
图4 分散系数对α估计结果的影响Fig.4 Influence ofγon estimation ofα

从图4可以看到,γ从0.1到10,本方法始终能正确估计α值。从估计均方误差结果可以看出,不同γ值下,α值估计的均方误差变化不大,且始终能保持－14 d B以下的均方误差,估计精度较高。

实验4 高斯噪声与SαS噪声共存时的估计效果

实验目的:验证高斯信号与SαS信号共存时算法对于α的估计效果。

实验方法:α取0.6,0.9,1.2,1.6,在SαS信号中掺杂入广义信噪比不同的高斯噪声,其他条件与前述实验相同,依据本算法估计信号α值。每种情况进行100次蒙特卡罗实验,记录α的估计结果均值和均方误差。

图5为高斯噪声掺杂时α的估计结果。

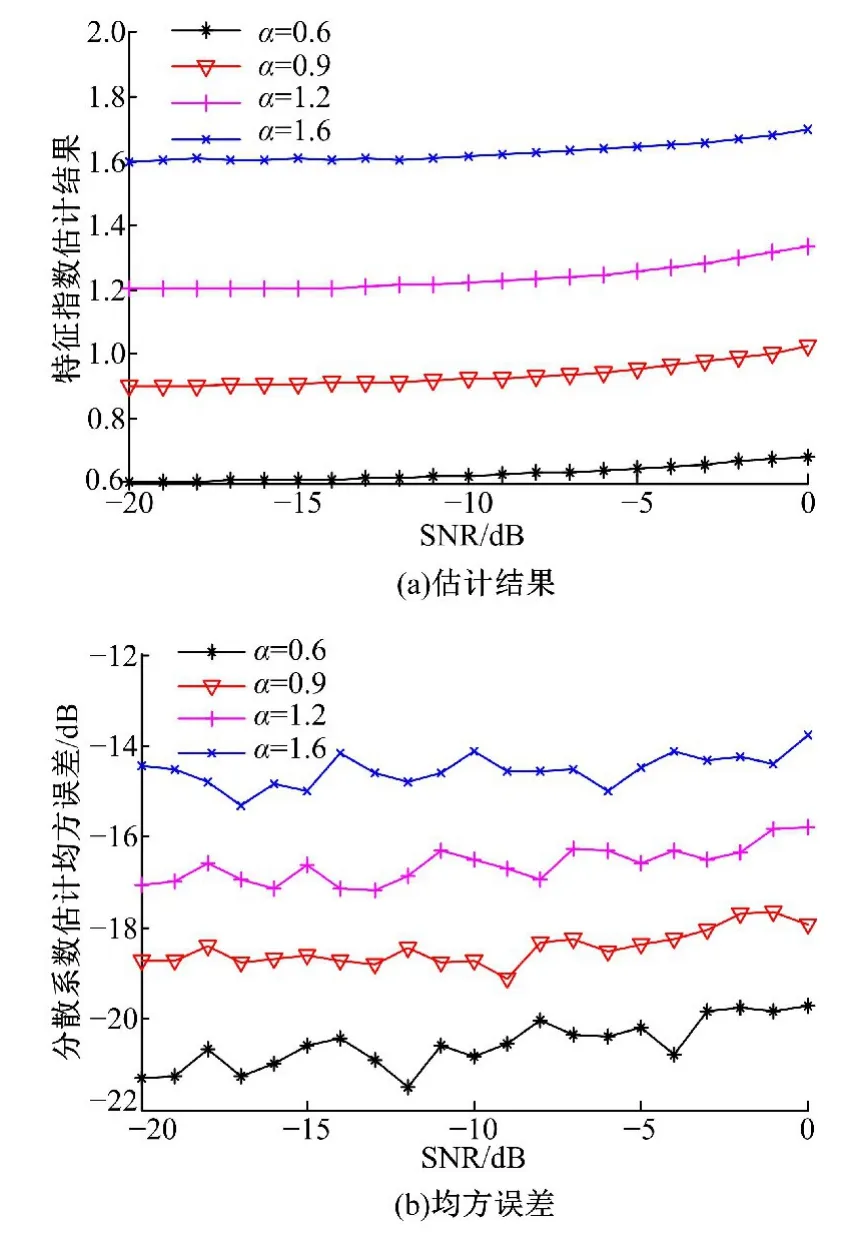
图5 高斯噪声掺杂时算法对α的估计结果Fig.5 Estimation ofαwhen Gaussian noise added

从图5可以看出,在信噪比0 d B以下,高斯噪声的添加对特征指数α估计结果的影响不大,估计均方误差在－8 d B以下。说明本算法可以估计高斯随机变量与α稳定分布随机变量共存时α稳定分布随机变量的特征指数。

4 结束语

针对α稳定分布信号处理中的参数估计问题,本文提出了基于α稳定分布p-范数和叠加性质的特征指数α估计方法。将α稳定分布随机变量的采集序列等分相加,结果序列的p范数与原序列的p范数之间存在的固定关系可以用来估计特征指数α。该方法不需要β的先验知识即可估计α值,在很大范围内可以正确估计α值。在0.1～2范围内,α值估计的均方误差均小于－13 d B,分段数和随机变量的γ变化对估计性能影响不大,在一定程度的高斯噪声与α稳定分布掺杂时,仍能正确估计α值。本文详细说明了算法原理和算法步骤,并证明了估计算法的无偏性和一致性。该方法可以为针对α噪声的信号处理算法提供特征指数α的先验知识,为基于分数低阶矩的算法提供阶次选择的依据。

[1]Schilder M.Some structure theorems for the symmetric stable laws[J].The Annals of Mathematical Statistics,1970,41(2):412-421.

[2]Weron A.Stable Processes and Measures:a Survey[M].Berlin:Springer,1983:306-364.

[3]Shao M,Nikias C L.Signal processing with fractional lower order moments:stable processes and their applications[J].Proceeding of the IEEE,1993,81(7):986-1010.

[4]孙永梅.α稳定分布参数估计与谱分析理论及应用研究[D].大连:大连理工大学信息与通信工程学院,2006.Sun Yong-mei.Study on the theory and application of parameter estimation and spectral analysis ofα-stable distribution[D].Dalian:School of Information and Communication Engineering,Dalian University of Technology,2006.

[5]李森.稳定分布噪声下通信信号处理新算法及性能分析[D].大连:大连理工大学信息与通信工程学院,2011.Li Sen.Communication signal processing new algorithms and performance analysis in stable noise[D].Dalian:School of Information and Communication Engineering,Dalian University of Technology,2011.

[6]何劲.α稳定分布噪声背景下阵列信号处理方法研究[D].南京:南京理工大学电子工程与光电技术学院,2007.He Jin.Investigation on array signal processing a midα-stable noise[D].Nanjing:School of Electronic and Optical Engineering,Nanjing University of Science and Technology,2007.

[7]Tsihrintzis G A,Nikias C L.Fast estimation of the parameters of alpha-stable impulsive interference[J].IEEE Trans on Signal Processing,1996,44(6):1492-1503.

[8]Ma X,Nikias C L.Parameter estimation and blind channel identification in impulsive interference[J].IEEE Trans on Signal Processing,1995,43(11):2884-2897.

[9]Kuruoglu E E.Analytical representation for positiveα-stable densities[C]∥IEEE International Conference on Acoustics,Hong Kong,2003:VI-729-32.

[10]Du Mouchel W H.Stable distributions in statistical inference:information from stably distributed samples[J].Journal of the American Statistical Association,1975,70(350):386-393.

[11]Brorsen B W,Ryongyang S.Maximum likelihood estimates of symmetric stable distribution parameters[J].Communications on Statisties－Simulation,1990,19(4):1459-1464.

[12]石屹然,赵晓晖,单泽彪,等.α和高斯噪声背景下线性极化阵列波达方向和极化参数联合估计的FLOCC-SMN方法[J].吉林大学学报:工学版,2016,46(4):1297-1303.Shi Yi-ran,Zhao Xiao-hui,Shan Ze-biao,et al.FLOCC-SMN method for DOA polarization parameters estimation of linear polarization array inαand Gaussian noise[J].Journal of Jilin University(Engineering and Technology Edition),2016,46(4):1297-1303.

[13]应文威,欧勇恒,蒋宇中,等.新型自适应非高斯接收机设计[J].吉林大学学报:工学版,2013,43(6):1685-1689.Ying Wen-wei,Ou Yong-heng,Jiang Yu-zhong,et al.New adaptive receiver for channels with non-Gaussian noise[J].Journal of Jilin University(Engineering and Technology Edition),2013,43(6):1685-1689.

[14]刘文红.脉冲噪声下时间延迟估计方法及应用的研究[D].大连:大连理工大学信息与通信工程学院,2007 Liu Wen-hong.Study on time delay estimation methods and applications in the presence of impulsive noise[D].Dalian:School of Information and Communication Engineering,Dalian University of Technology,2007.