基于沙蝎定位猎物的仿生震源定位方法

王 柯,刘 富,2,康 冰,霍彤彤,周求湛,2

(1.吉林大学 通信工程学院,长春130022;2.吉林大学 汽车仿真与控制国家重点实验室,长春130022)

0 引 言

振动监控在安全监控中广泛应用,是用于映射非常规刺激不可或缺的工具[1,2]。振动监控的关键在于诱发振动事件的定位。随着电子和通信技术的快速发展,定位技术也有了显著提升,定位速度和准确性都有了明显的进步。振动监控系统的任务是检测和识别震源信号。振动接收器接收运动目标或其他振动事件产生的波信号。目标的类型和位置都是通过对震源信号的分析和判断得到的。振动监控系统可以实现全天候不间断的监控工作,不断接收振动信号,不需要额外的复杂装置进行辅助,同时不受光线和视觉的限制,有很好的隐蔽性。振动监控系统是一种被动监控模式,可以进行大面积的实时监控。震源定位常用的方法有时差定位法(Time difference of arrival,TDOA)和地震发射层析成像法[1](Seismic emission tomography,SET)等。TDOA方法需精确提取波的初至时间,但实际监测过程中,通常地震监测信号会受到干扰,所以震源定位计算出的结果误差较大。SET方法不需要提取地震波的初至时间,但需要通过增加监测站点数量解决微震信号信噪比低的问题。为解决上述问题,本文模拟沙蝎定位机理,设计了一种新的仿生定位方法来定位震源,这种仿生定位方法既不需要准确的到时提取,也不需要大量的监测点。

沙蝎由于其灵敏的振动定位技能,近几年受到广泛关注[3-5],Stürzl等[6-8]提出了一种沙蝎定位理论,并且该理论能有效运用在对目标定位的应用中。在Stürzl的理论中利用神经网络对震源信号进行脉冲编码,决策系统通过编码的信号对目标进行定位。其中,神经网络是整个定位过程的核心环节,模拟神经网络中神经元发射脉冲是仿生定位的主要内容。Hodgkin-Huxley(HH)模型[9]是公认的最接近真实生物神经元的数学模型,它能准确地描述神经元之间神经冲动的产生和传递。然而,无论是程序仿真或者电路模拟来实现H H模型都十分复杂。所以,研究人员在H H模型的基础上提出了简化模型,例如整合发射模型[10](Integrate and fire model,I&F)和脉冲响应模型(Spike response model,SRM)等。简化模型容易实现,并且计算速度快,在此基础上进一步简化神经网络,进行仿生震源定位,减小算法复杂度。

Adams等[7]提出了一个完整的方向确定和距离估计的方法,其中借鉴了Stürzl的沙蝎定位理论,但是Adams设计的执行控制器只实现了模拟状态下的数据计算并用仿真软件实现;Garreau等[8]提出并实现了一个基于Stürzl的沙蝎定位理论的实时定位模型,该模型使用的是5个接收器,但是其响应结果并不理想。本文应用了Stürzl的理论提出并实现了一个单一事件的震源定位模型。与Garreau方法[8]不同的是本文采用8个接收器。为了减小响应角度与目标角度的差,考虑到生物进化的选择性,本文对接收器重新进行了排布,使其更适用于实际定位系统,同时与TDOA算法进行了对比。最后,在一个开阔的区域进行了实际数据的定位实验以验证该定位方法的有效性。

1 沙蝎定位理论

在自然界中,许多物种通过地面传播的“声音”进行交流或发现猎物,例如八足节肢动物,其中包括蜘蛛和沙蝎。沙蝎生活在沙漠中,它的食物主要是一些小的昆虫和它的同类。沙蝎是夜间行动的动物,眼睛是退化的,白天待在地下30 cm左右的洞穴中以逃避地表超过60℃的高温。日落后它才出现在沙地上等待它的猎物。基跗节复合缝感受器(Basitarsus composite slits sensilla,BCSS)是沙蝎腿部末端的能接收振动信号感觉器官[11],可以感觉到十分微小的变化,十分灵敏。BCSS可以接收到低速低频的由基质传播的表面波。

BCSS分布在R≈2.5 cm的圆周上,如图1所示,其角度分别为:

其向前行走的方向为0°,编号是从右前腿开始顺时针编号k＝1,2,…,8。运动的猎物会在基质上产生振动信号,沙蝎通过基质传递的振动信号定位猎物的方向[12]。定位到猎物后,沙蝎先转动身体再前进捕捉猎物。对于一个给定的刺激角度φs,波到达任意两个分别在γk、γl方向上的BCSS的时间差为:

式中:v R为振动波在基质中传播的速度。

图1 沙蝎BCSS分布图Fig.1 Distribution of sand scorpion’s BCSS

沙蝎的感觉器官接收震源信号后其定位过程如图2所示。BCSS接收运动目标产生的振动信号后将其转化为电信号传递给感觉神经元,感觉神经元将感觉输出传递给指令神经元,对指令神经元产生兴奋作用,然后在兴奋与抑制的共同作用下指令神经元对振动信号进行脉冲编码,根据编码大脑决策出响应方向,最后响应结果会传递给运动系统。

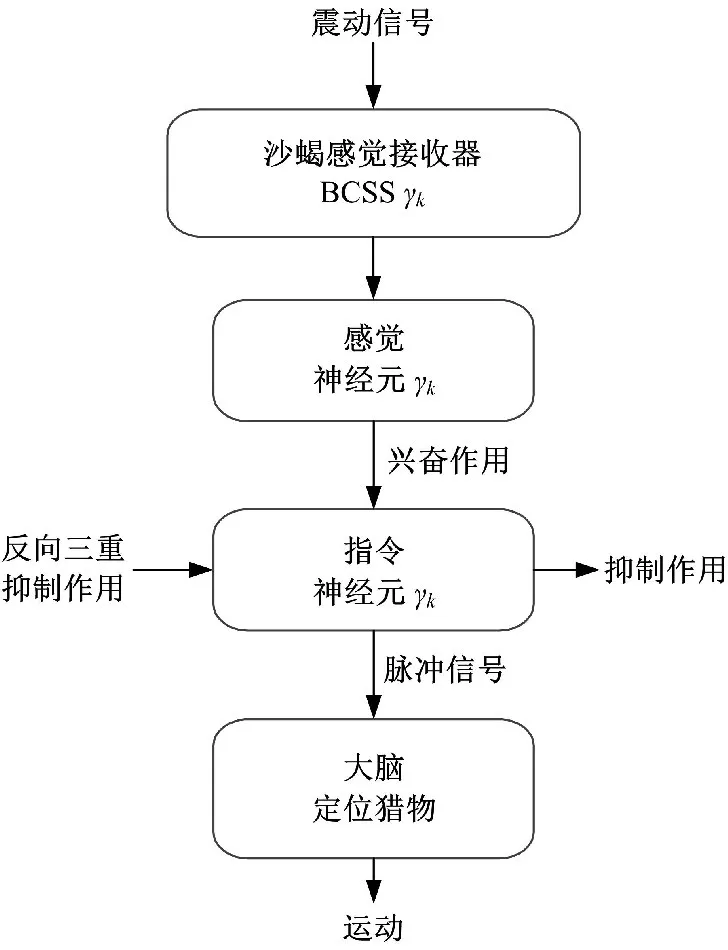
图2 沙蝎定位过程Fig.2 Sand scorpion’s locating process

基于沙蝎传递信号的过程对神经网络的信号相互作用进行设定。假设γk k(＝1,2,…,8)方向的接收器可以激活一个感觉神经元,即每个方向都有一个感觉神经元,每个感觉神经元连接一个指令神经元,如图3所示。γk方向上的被激活的感觉神经元将信号传递给γk方向上的指令神经元,激活该指令神经元,同时指令神经元激活中间性抑制神经元抑制其反方向和的3个指令神经元。因此,每个指令神经元的输入信号都构成一个3/1构型[6],即一个兴奋输入和三重抑制输入。指令神经元依据3/1构型对振动信号进行编码。

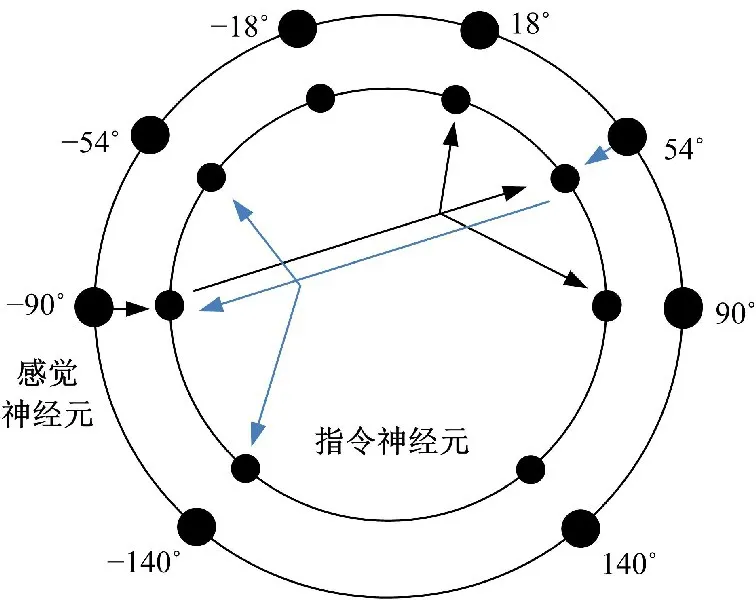
图3 神经元分布及指令神经元的抑制作用Fig.3 Diagram of inhibitory effect of eight command neurons

2 本文方法

2.1 脉冲发射模型

I&F模型是最常用的HH神经元简化模型之一,它把细胞膜看成电阻和电容的组合,把多个离子通道用一个电阻进行简化。神经元模型具有以下3个基本特点:

(1)输入信号电势的累积。

(2)当膜电势达到一定阈值时发射一个脉冲,以此来传递信号的相关信息。

(3)膜电势释放后,神经元进入绝对不应期,无论多大刺激都不会做出反应。

当膜电势到达一定阈值时就会产生一个脉冲。因此,依据I&F模型以及神经元基本特征,进一步用一个脉冲发射模型替代指令神经元进行简化,如图4所示,其表达式为:

式中:I k(t)为第k个指令神经元的输入信号;E为静息电势;电阻R和电容C为脉冲发射模型的参数;u k(t)为指令神经元的膜电势。

不同的输入信号将产生不同的脉冲信号。脉冲发射模型将电信号转换成脉冲信号进行编码,同时保留了定位目标的信息。

图4 脉冲发射模型Fig.4 Spike firing model

在本文的工作中,8个方向上各有一个脉冲发射模型。接收器接收到目标产生振动信号后将信号传递给脉冲发射模型。由于信号到达时间的不同以及3/1构型的相互作用,脉冲发射模型会将信号转换成8个方向上的不同脉冲数。

2.2 基于脉冲发射模型的仿生震源定位

指令神经元受到刺激并达到一定阈值就会发射脉冲,由于3/1构型的存在使得各个指令神经元发射脉冲数不同。γk方向上的指令神经元先接收兴奋信号就会先对其反向的的指令神经元产生抑制作用,同样的,反向的指令神经元接收到兴奋信号输入也会对γk－1、γk和γk＋1产生抑制作用。γk的中间性抑制神经元被激活后,抑制作用从该神经元传递到反向的指令神经元的时间为ΔI,所以抑制作用输入到反向指令神经元会产生一定延迟,并不是马上产生抑制作用,但是在抑制作用到达前γk的指令神经元就已经由于兴奋作用而发射脉冲了。兴奋和抑制输入指令神经元的时间差与发射的脉冲数成正比关系,这就是3/1构型作用的结果。

沙蝎在定位猎物时是静止不动的,而且在走动时不进行定位,所以沙蝎的感觉接收器在定位过程中是在固定位置的,而BCSS在－90°～90°分布是相对密集的,也就是沙蝎向前行走的方向。因此,在各个方向上的定位权重相同的情况下,认为沙蝎在－90°～90°的范围内定位更为准确。定位到猎物后,沙蝎先是转向猎物,然后前进捕捉猎物。生物在漫长的进化过程中都是经过环境选择的,所以沙蝎BCSS的分布也是进化选择的结果,由于BCSS位于腿部末端,其首要满足的是便于走动,其次是定位功能。在实验中脉冲发射模型不需要移动,所以在定位时需要在各个方向有同样的平均误差,因此本文将接收器的角度重新设定为:

设圆心为原点,90°方向为x轴,0°方向为y轴,以此建立坐标系,则接收器坐标(x k,y k)为:

在神经科学中,群向量(Population vector)是一群有各自喜好方向的神经元向量的求和。van Hemmen等[13]提出动物的运动可以用矢量来描述,即:

式中:n为群向量;υi为神经元放电率;ℓi为神经元的喜好方向。

运动是依靠神经编码来发出具体的运动指令,如果把发出运动指令的神经元的放电活动用向量来表示,向量的方向是这个神经元的喜好方向,向量的长度是神经元放电率,把所有能记录到的神经元的“放电向量”用向量求和的方式加起来,得到的向量方向就是运动的目标方向。群向量编码是一个执行器,其输出代表一个响应动作,在本文中输出的是振动事件的响应角度,指令神经元是用来进行编码发出运动指令的神经元,γ′k是指令神经元的喜好方向,神经元发射的脉冲数代表放电率。因此,通过群向量编码形成了一个从震源信号到定位角度的映射。

由于三重抑制作用使得不同角度上脉冲神经元产生的脉冲数不同,定义第k个脉冲发射模型发射的脉冲数为n k(k＝1,2,…,8)。n k的大小与信号到达接收器的时间差有关。信号越早到达,脉冲数n k越大。对于先接收到信号的脉冲发射模型来说,在抑制性输入到达之前,脉冲发射模型就会在兴奋输入作用下先发射脉冲。所以8个脉冲发射模型发射的脉冲数的集合就是对振动信号的编码。因此,利用脉冲数进行的群向量编码为:

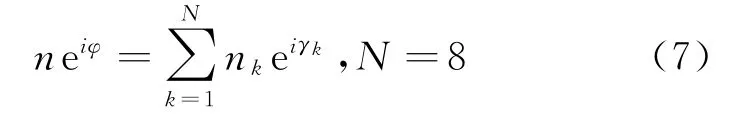
则计算得到定位角度公式为:

式中:neiφ为整体向量;相角φ即为振动事件定位的响应角度;n为模长。

3 实 验

3.1 接收器不同分布的对比实验

在仿真实验中,本文使用了沙蝎定位环境的自然参数:振动波在基质中传递的速度为v R＝50 m/s,感觉接收器分布在R≈2.5 cm的圆周上,角度为γ′k。振动信号设置为一个没有衰减和噪声干扰的理想信号。在相同的时间信息下,利用模拟的振动信号对BCSS的角度分布γk和新设定的角度分布γ′k进行对比,结果如图5所示,其横轴为输入信号角度,是从－180°到180°且间隔为1°的模拟震源信号;纵轴为误差角度,是输入信号的目标角度与定位的响应角度之差。从结果可以看出,改进的接收器分布角度对方向的定位效果更好,定位误差明显减小,同时也说明了BCSS的分布使得沙蝎在前进方向的定位误差相对较小。

图5 接收器不同分布的误差对比Fig.5 Error comparison in different distribution of receiver

3.2 仿生定位方法与TDOA方法的对比实验

TDOA算法是对TOA(Time of arrival)算法的改进,它不是直接利用信号到达时间,而是用多个接收器接收到信号的时间差来确定目标位置,与TOA算法相比它不需要加入专门的时间戳,定位精度也有所提高。TDOA值的获取一般有两种形式:第一种形式是利用目标到达两个接收器的时间TOA,取其差值来获得;第二种形式是将一个接收器接收到的信号与另一个接收器接收到的信号进行相关运算,从而得到TDOA的值,再进行定位计算能获得较高精度。TDOA更具有实际意义,这种方法对网络的要求相对较低,并且定位精度较高。

震源到接收器之间的信号传输是一条直线,则有下面的等式:

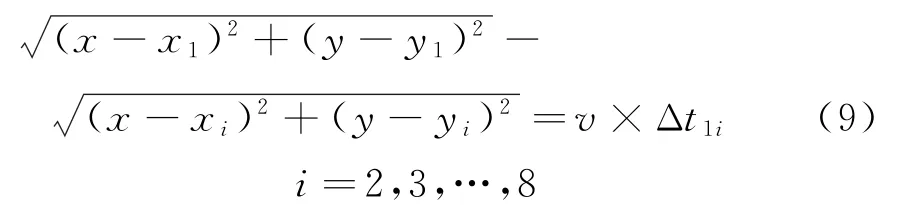
式中:(x,y)为震源点坐标;(x1,y1)为1号接收器坐标;(x i,y i)为2～8号接收器坐标。

本文利用式(9)的TDOA方法与仿生定位方法进行对比,结果如图6所示,其中横轴为输入信号角度,是从－180°到180°且间隔为1°的模拟震源信号;纵轴为误差角度,是输入信号的目标角度与定位的响应角度之差。统计数据的比较如表1所示,从表中可以看出,仿生方法的定位方向的误差明显小于TDOA方法。TDOA方法是一种相对简单的定位方法,但是该方法需要提取波的到时进行定位,无法避免提取时产生的误差,且目前还没有公认准确的应用于到时提取的方法,所以使用仿生方法以避免到时提取产生的误差。图6中TDOA方法的结果接近正弦曲线,这与TDOA方法的双曲线定位公式有关。

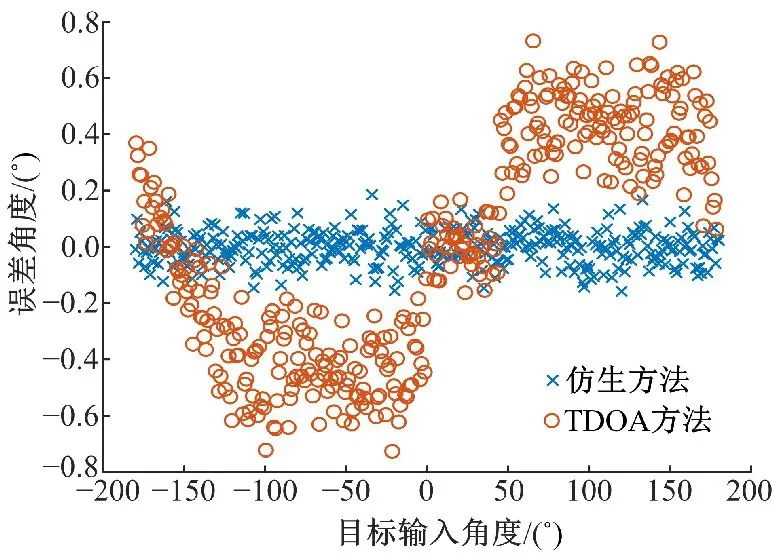
图6 仿生方法与TDOA方法的对比Fig.6 Error comparison between bionic method and TDOA method

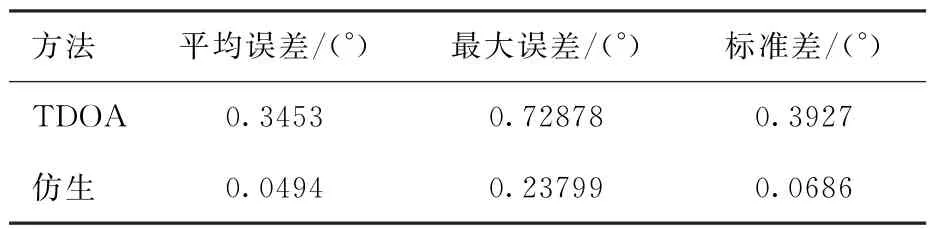
表1 定位误差的统计数据对比Table 1 Statistical data comparison of locating errors

3.3 真实数据实验

真实震源数据是在一块开阔的土地上,一个铅球在指定高度(h＝20、40、60 cm)落下而采集的振动信号。接收器布置如图7所示,按照均匀分布的γ′k布置,为确保在不同接收器采集到的信号有足够的时间差,设置分布半径为1 m。采集的震源信号分为两个定点:(1,2.5)和(1,3.5),其中,(1,2.5)采集47组,(1,3.5)采集29组,共有76组,具体情况如表2所示,实验的数据处理均是在MATLAB上完成。采集的一组振动数据如图8所示,即不同的通道采集到的不同幅值和到时的信号代表同一个震源信号。将振动信号输入给脉冲发射模型得到脉冲数,然后利用群向量编码式(8)得到定位角度。

图7 接收器的布置Fig.7 Arrangement of sensors

表2 不同高度下采集的数据数量Table 2 Number of collected data in different heights

图8 一组振动信号Fig.8 A set of vibration signals

76组数据定位的平均误差为4.9310°,最大和最小误差分别为13.527°和0.1169°。在实验过程中采用不同的高度代表不同的信噪比,具体结果如表3所示。随着信噪比的降低,定位误差增大,故信号越弱对仿生定位方法的影响越大。仿生方法与TDOA方法的结果对比如表4所示,从表中可以看出仿生方法比TDOA方法更稳定,平均误差更小,定位效果更好。

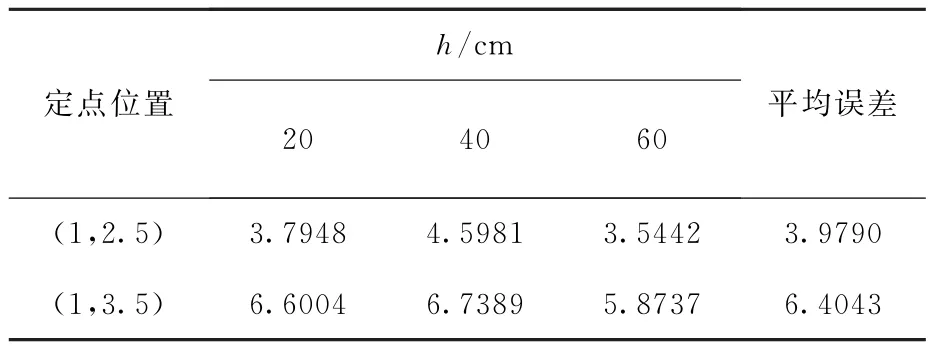
表3 真实数据误差结果Table 3 Error results of real data(°)

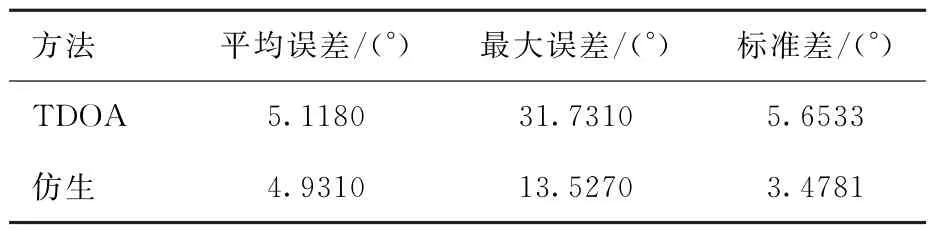
表4 仿生方法与TDOA方法真实数据结果对比Table 4 Comparison of TDOA method and method in this paper of real data

4 结束语

仿生方法吸取了沙蝎定位中不需要提取信号初至时间的优点,避免了初至提取时造成的误差。本文根据实际情况改进接收器分布,并认为BCSS接收器官是为了定位后便于移动的生物进化选择的结果。通过实验结果可以看出,改进后的定位结果误差更小、更适用于定位。另外本文对比了仿生方法与TDOA方法,在理想环境下仿生方法的误差明显小于TDOA方法。在理想环境下误差小于1°,但是在实际应用中噪声干扰是不可避免的,因此在真实环境下采集了振动数据验证了仿生定位方法的有效性,平均定位误差为4.9310°,而且定位误差随着信噪比的减小而增大,同时比TDOA方法定位精度高。接下来的工作将是减小信噪比对定位方向的影响,定位信噪比较低的振动信号,并在此基础上定位出震源目标的距离。

[1]Zhebel O,Eisner L.Simultaneous microseismic event localization and source mechanism determination[J].Geophysics,2015,80(1):1-9.

[2]Anikiev D,Valenta J,Stanek F,et al.Joint location and source mechanism inversion of microseismic events:benchmarking on seismicity induced by hydraulic fracturing[J].Geophysical Journal International,2014,198(1):249-258.

[3]van Hemmen J L.Neuroscience from a mathematical perspective key concepts,scales and scaling hypothesis,universality[J].Biological Cybernetics,2014,108(5):701-712.

[4]Li Y M,Li S,Ge Y J.A biologically inspired solution to simultaneous localization and consistent mapping in dynamic environments[J].Neurocomputing,2013,104:170-179.

[5]Jeong E S,Kim D E.Detecting the direction of vibration inspired by prey detection behavior of sand scorpions[J].Journal of Institute of Control,Robotics and Systems,2012,18(10):947-954.

[6]Stürzl W,Kempter R,van Hemmen J L.Theory of arachnid prey localization[J].The American Physical Society,2000,84(24):5668-5671.

[7]Adams S V,Wennekers T,Bugmann G,et al.Application of arachnid prey localisation theory for a robot sensorimotor controller[J].Neurocomputing,2011,74(17):3335-3342.

[8]Garreau G,Proxenou E,Andreou A G,et al.Person localization through ground vibrations using a sand-scorpion inspired spiking neural network[C]∥Proceedings of the 47th Annual Conference on Information Sciences and Systems(CISS)IEEE,Baltimore,MD USA,2013:1-4.

[9]Hodgkin A L,Huxley A F.A quantitative description of membrane current and its application to conduction and excitation in nerve[J].The Journal of Physiology,1952,117(4):500-544.

[10]Brunel N,van Rossum M C W.Lapicque′s 1907 paper:from frogs to integrate-and-fire[J].Biological Cybernetics,2007,97(5/6):337-339.

[11]Brownell P,Farley R D.Detection of vibrations in sand by tarsal sense organs of the nocturnal scorpion,paruroctonus mesaensis[J].Journal of Comparative Physiology A,1979,131(1):23-30.

[12]Brownell P H,van Hemmen J L.Vibration sensitivity and a computational theory for prey-localizing behavior in sand scorpions[J].Amerzool,2001,41(5):1229-1240.

[13]van Hemmen J L,Schwartz A B.Population vector code:a geometric universal as actuator[J].Biological Cybernetics,2008,98(6):509-518.