三维毫米波通信系统的性能分析

陈瑞瑞,张海林

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室,西安710071)

0 引 言

随着高清视频传输、实时视频会议以及在线视频教育等服务的出现,用户对移动通信的传输容量提出了更高的要求[1]。尽管多输入多输出(Multiple input multiple output,MIMO)技术可以随天线数的增加而成倍提高移动通信的容量[2,3],但其通常采用的10 GHz以下的微波通信已经难以满足用户对视频服务的需求。毫米波通信可以提供更大的传输带宽,且其波长更短,可在收发两端配置更多天线以获得复用增益从而提高传输容量[4]。因此,毫米波通信已成为5G通信的研究热点[5]。然而,毫米波频率较高,会引起较大传播路径损耗,将导致视距路径(Line-of-sight,LOS)能量大于非视距路径(Non-LOS,NLOS)能量。毫米波通信信道主要由LOS信道所决定,因此可获得的系统容量将很大程度上依赖于天线的配置[6-9]。

为了研究毫米波通信系统的容量性能,本文建立了一种基于均匀线阵的三维MIMO信道模型。当系统容量达到最大时,基于信道的正交条件,本文推导出了最优天线间距。通过最优天线间距的表达式可以看出最优容量与载波波长、天线数、收发天线距离以及天线配置之间的关系。然后,分析了天线数的增加所引起的性能变化。最后,本文定义了偏差因子以研究天线间距偏差对毫米波通信容量的影响。

1 系统模型

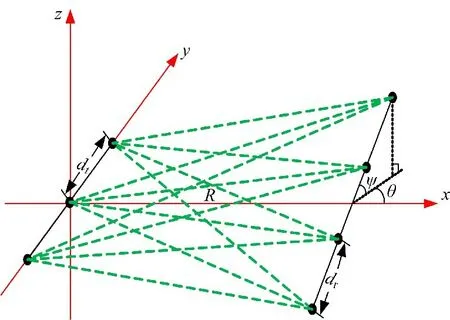
图1 三维空间坐标系Fig.1 Three-dimensional coordinate system

研究三维空间下的毫米波通信,发射和接收天线阵列都是均匀线阵,其发射和接收天线数分别为Nt和Nr,天线间距分别为dt和dr。如图1所示,建立三维坐标系,将发射天线阵列的中心作为三维坐标系的中心,发射与接收天线阵列的中心连线作为x轴,发射天线阵列方向为y轴,垂直于x-y平面的方向作为z轴。同时,将发射与接收天线阵列中心之间的距离定义为R。接收天线阵列与x-y平面所形成的夹角定义为ψ。接收天线阵列在x-y平面上的投影与x轴所形成的夹角定义为θ。根据所建立的三维坐标系,第m根发射天线的坐标为:

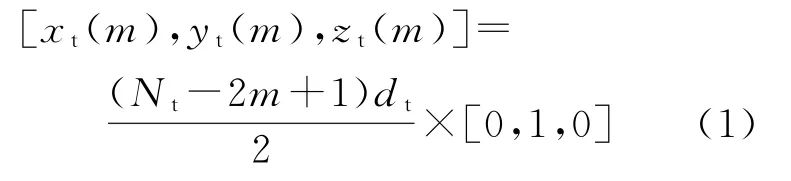
式中:m＝1,2,…,Nt。

第n根接收天线的坐标为:

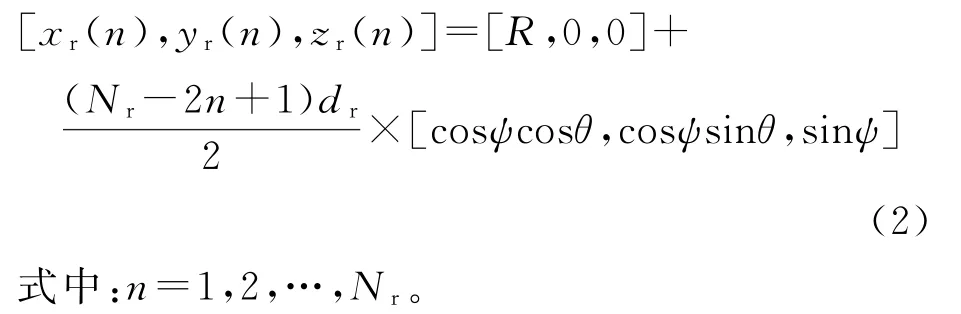
在毫米波通信环境下,第m根发射天线到第n根接收天线之间的信道系数为[10]:

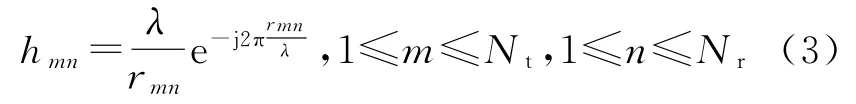
式中:λ为载波波长;r mn为第m根发射天线到第n根接收天线之间的距离。

式中:r∈CNr×1表示接收信号向量;s∈CNt×1表示发射信号向量;n∈CNr×1表示均值为0的加性高斯白噪声,且,ξ{·}和(·)H分别表示取数学期望和共轭转置,表示噪声功率,I Nr表示Nr×Nr的单位矩阵。

定义Q＝ξ{ssH}为发射信号的协方差矩阵。在实际应用中,发射功率通常被平均分配到Nt根发射天线上。当发射信号的总功率为P T时,Q＝(PT/Nt)I Nt。此时毫米波通信系统的信道容量可以表示为[2]:

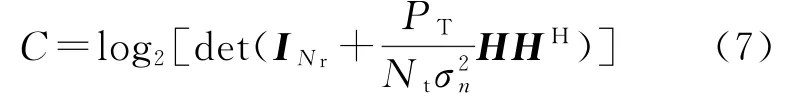
2 最优天线间距

由文献[6]可知要使毫米波通信系统获得最大容量,就要保证信道不同行向量之间的内积为0。设H的行向量为h n＝[h n1,h n2,…,h nNt],则:

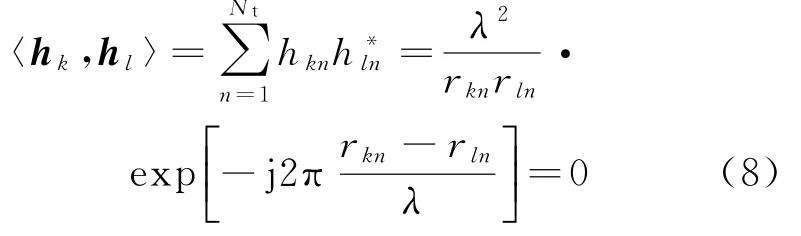
为了方便数学计算,将r mn改写为:

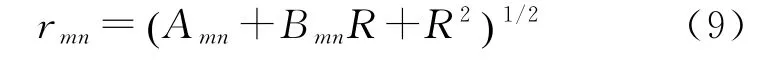
对于任意的k,l,n,有

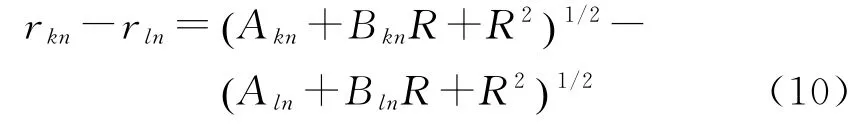
当R足够大,即1/R→0时,运用二阶泰勒扩展公式可得:

注意到,对于任意n＝1,2,…,Nr,b n＝b1＋(n－1)dr,故式(11)可以改写为:

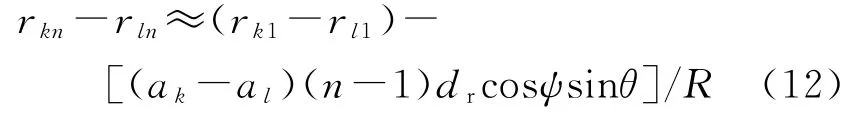
因此,对于任意的k和l,公式(8)可以近似为:

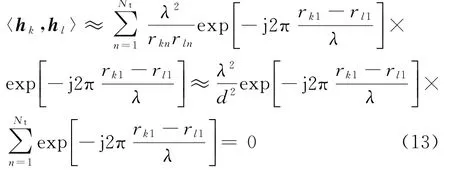
求解式(13)可以得出最优化的天线间距为:

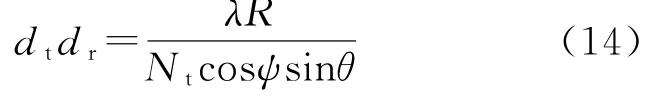
3 空间自由度及天线间距偏差分析

当最优化条件(14)满足时,矩阵HHH会有Nt个相同的特征值。因此,毫米波通信系统的最大空间自由度就是Nt。为了便于分析,本文仅考虑发射天线数和接收天线数相等的情况,即Nt＝Nr。发射天线阵列和接收天线阵列的总长分别定义为LT和LR,并将毫米波通信系统所能获得的最大空间自由度定义为Nmax。当LT和LR给定时,发射天线间距和接收天线间距分别为dt＝LT/(Nmax－1)和dr＝LR/(Nmax－1),由最优化天线间距的条件可推导出毫米波通信系统的最大空间自由度:

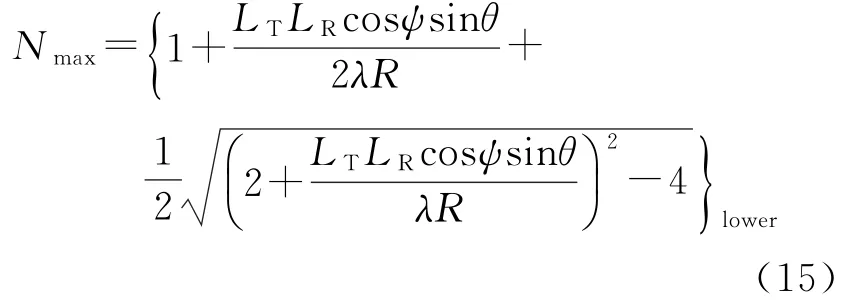
式中:{·}lower表示向下取整。

式(15)给出了当发射天线阵列总长LT和接收天线阵列总长LR确定时毫米波通信系统所能获得的最大空间自由度。

继续分析实际天线数超过Nmax时毫米波通信系统的性能变化。设ψ＝0,θ＝π/2,即收发天线阵列平行时,考虑两种不同情况下的信道矩阵特征值变化:

(1)满足最优化天线间距条件,其中Nt＝Nr＝4,λ＝10 mm,R＝100 m。

(2)天线数为Nt＝Nr＝16,λ＝10mm,R＝100m。

对以上两种情况的信道矩阵进行特征值分解,并对所获得的特征值进行归一化可以得到如图2所示的结果。从图2可以看出,满足最优化天线间距时信道将会产生4个相等的特征值,而天线数增加到16时主要是增大了前4个特征值,其余的特征值则会迅速地衰减。也就是说,满足最优化天线间距时信道的最大空间自由度为Nmax＝4,当天线数成倍增加时空间自由度并没有相应地增加。因此,增加天线的数目主要是增大了前Nmax个特征值,即主要增加了信道的功率增益,并没有相应地增加空间自由度。

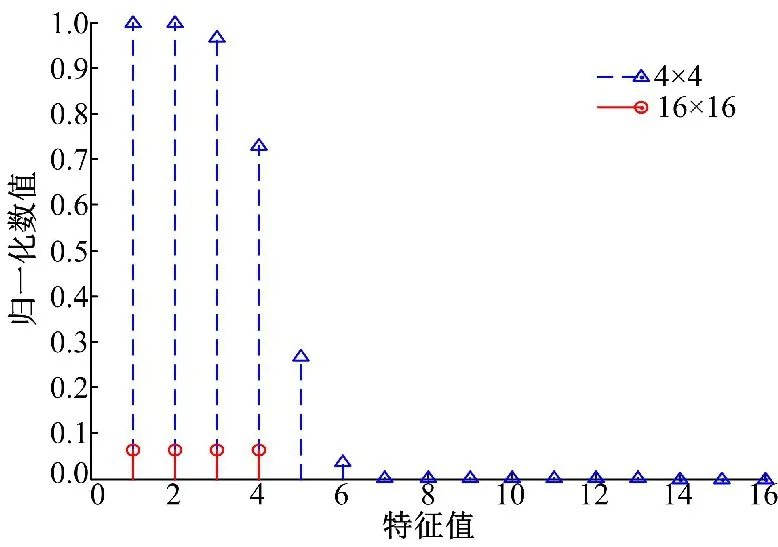
图2 矩阵HHH的特征值Fig.2 Eigenvalues of matrix HHH

在实际应用中,最优天线间距是不容易实现的。这主要是因为最优天线间距所需要的间距太大,难以实现。其次,最优天线间距只是针对一个载波频率,当系统中存在多个不同频率的载波时必然会产生偏差。为了研究天线间距偏差对容量的影响,定义偏差因子dev:

当偏差因子dev等于1时,说明实际的天线间距即为最优天线间距;dev大于1时,实际的天线间距小于最优天线间距;dev小于1时,实际的天线间距大于最优天线间距。本文采用中断容量来分析dev所造成的容量偏差。中断概率为Pout(Cout)＝Pro(C≤Cout),Cout表示中断容量。

4 仿真结果与分析

首先分析天线间距偏差对容量的影响。仿真中,信噪比为15 d B,偏差因子dev分别取0 d B和30 d B,即最优天线间距和较大天线间距偏差的情况。信道为莱斯信道,且莱斯因子K分别设为－20、0、20 d B。仿真结果如图3所示。

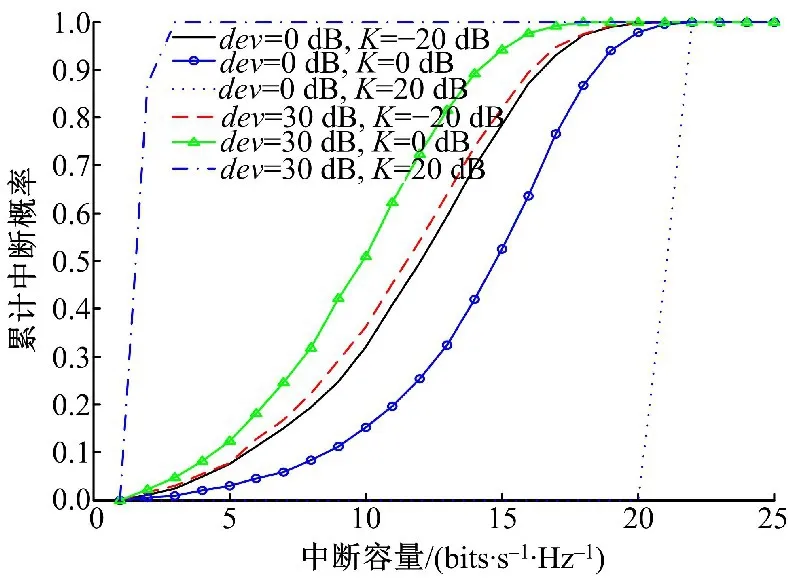
图3 4×4 MIMO系统的中断容量Fig.3 Outage capacity of 4×4 MIMO system

由图3可以看出,当莱斯因子K为20 d B时,dev越大则会造成越大的容量损失。而当莱斯因子K越小时,dev对容量的影响也就越小。同时也要注意到,当莱斯因子K为－20 dB时,dev基本不会对容量造成影响。这是因为莱斯因子K越小时,信道的随机性就越强,dev的影响也就相应降低了。但当莱斯因子K较大时,dev的影响也就越来越大。当莱斯因子K为20 dB时,dev为0 dB,即最优天线间距时容量性能是最优的,这同样也说明了毫米波通信系统的性能是优于传统MIMO系统的。

在图3的仿真中仅仅比较了4×4MIMO系统在不同偏差因子dev和不同莱斯因子K下的中断容量,而没有体现出毫米波通信系统与传统MIMO通信系统性能随天线数目的变化。因此,图4给出了K＝0 dB莱斯信道下2×2,4×4毫米波通信系统,K＝0 dB莱斯信道下单输入单输出(Single input single output,SISO)通信系统和瑞利信道下2×2,4×4传统MIMO通信系统的中断容量对比。

在图4的仿真中,设偏差因子dev为0 d B。

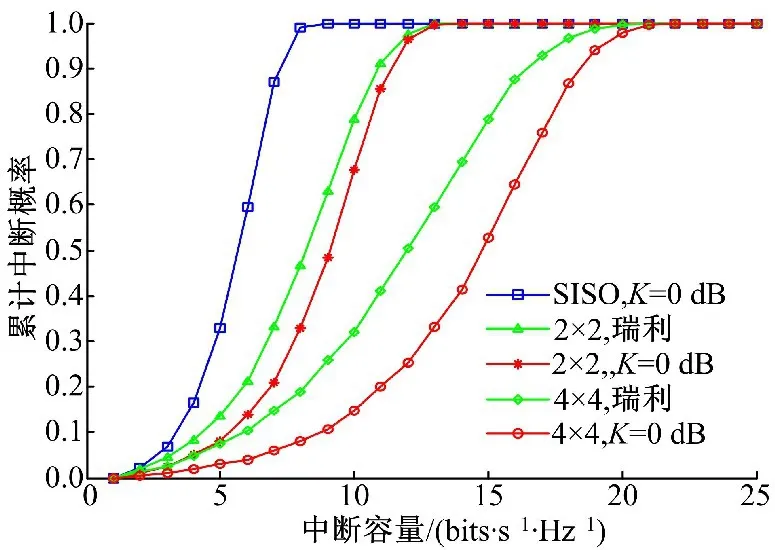
图4 不同天线数的系统对比Fig.4 Comparison of systems with different antenna number

从图4可以看出,莱斯信道下毫米波通信系统的性能优于瑞利信道下传统MIMO通信系统和莱斯信道下SISO通信系统,并且瑞利信道下传统MIMO通信系统的性能优于莱斯信道下SISO通信系统。当收发天线数目增加时,莱斯信道下毫米波通信系统,瑞利信道下传统MIMO通信系统和莱斯信道下SISO通信系统之间的性能差距将会变大。

为了进一步验证毫米波通信系统的优势,本文将对比固定天线间距毫米波通信系统,最优天线间距毫米波通信系统,瑞利信道下传统MIMO系统和莱斯信道下SISO系统的容量。仿真中,设发射和接收天线数相等:Nt＝Nr＝4,信噪比为10 dB。对固定天线间距毫米波通信系统,设dt＝dr＝0.5 m,且收发天线阵列的配置分别为θ＝π/2,ψ＝0和θ＝π/6,ψ＝π/4。对最优天线间距毫米波通信系统,根据实际应用的限制,天线间距的最大值可设为dt,max＝dr,max＝1.5 m。为了达到最优容量,基于最优化条件(14),设发射天线间距和接收天线间距相等,即。因此,根据实际应用的限制,在仿真中设发射天线间距,且将毫米波通信系统的接收天线间距设置为。为了对比,本文也给出了莱斯信道下SISO系统容量以及瑞利信道下4×4 MIMO系统容量的仿真曲线。

由图5可以看出,当毫米波通信系统天线间距取固定值时,信道容量会随着距离R的增加周期性变化,且随着R→∞而C→log2( 1＋ρNr),其中ρ为信噪比。同时也要注意到收发天线阵列配置为θ＝π/6,ψ＝π/4要比θ＝π/2,ψ＝0更快地衰减为log2( 1＋ρNr),这是由于θ＝π/2,ψ＝0的配置更接近最优天线配置。满足最优天线间距的毫米波通信系统容量会在一定范围内保持在最优值,但也会随R的不断增加而衰减为log2(1＋ρNr)。最优容量的保持范围主要是由天线间距的最大值dt,max和dr,max所决定的。通过与瑞利信道下MIMO系统的容量进行对比可以看出,在天线间距最大值dt,max和dr,max所允许的范围内,毫米波通信系统的容量得到了显著提升。

图5 容量对比Fig.5 Capacity comparison

5 结束语

对三维空间下的毫米波通信系统进行了性能分析。基于信道的正交性,本文推导出了获得最大系统容量的最优天线间距。然后,分析了天线数的增加以及天线间距偏差所引起的性能变化。通过计算机的仿真结果可以看出,当收发天线距离在一定范围时,最优天线间距可以保证毫米波通信系统获得最大容量,且超过了瑞利信道下传统MIMO系统的容量。

[1]Wang P,Li Y,Yuan X,et al.Tens of gigabits wireless communications over E-band LoS MIMO channels with uniform linear antenna arrays[J].IEEE Transactions on Wireless Communications,2014,13(7):3791-3805.

[2]Goldsmith A,Jafar S A,Jindal N,et al.Capacity limits of MIMO channels[J].IEEE Journal on Selected Areas in Communications,2003,21(5):684-702.

[3]陈健,李佳龙,阔永红.AF-MIMO系统机会中继选择算法[J].吉林大学学报:工学版,2014,44(6):1818-1824.Chen Jian,Li Jia-long,Kuo Yong-hong.Opportunistic relay selection algorithm for AF-MIMO system[J].Journal of Jilin University(Engineering and Technology Edition),2014,44(6):1818-1824.

[4]Cai W,Wang P,Li Y,et al.Deployment optimization of uniform linear antenna arrays for a two-path millimeter wave communication system[J].IEEE Communications Letters,2015,19(4):669-672.

[5]Sun S,Rappaport T S,Heath R W,et al.MIMO for millimeter-wave wireless communications:beamforming,spatial multiplexing,or both?[J].IEEE Communications Magazine,2014,52(12):110-121.

[6]Torkildson E,Madhow U,Rodwell M.Indoor millimeter wave MIMO:feasibility and performance[J].IEEE Transactions on Wireless Communications,2011,10(12):4150-4160.

[7]Bøhagen F,Orten P,Øien G E.Design of optimal high-rank line-of-sight MIMO channels[J].IEEE Transactions on Wireless Communications,2007,6(4):1420-1425.

[8]Bohagen F,Orten P,Oien G E.Construction and capacity analysis of high-rank line-of-sight MIMO channels[C]∥IEEE Wireless Communications and Networking Conference,New Orleans,USA,2005:432-437.

[9]Su W,Matyjas J D,Gans M J,et al.Maximum achievable capacity in airborne MIMO communications with arbitrary alignments of linear transceiver antenna arrays[J].IEEE Transactions on Wireless Communications,2013,12(11):5584-5593.

[10]Rappaport T.Wireless Communications:Principles and Practice[M].2nd ed.New Jersey:Prentice Hall,2002.