亚瑞利散斑场的二阶累积量鬼成像

李金遥，姚治海，王晓茜，赵环

（长春理工大学 物理学院，长春 130022）

鬼成像（GI）又称为双光子成像，是传统光学成像与现代信息技术相结合的新型成像手段。与传统的成像方案不同，GI 利用二阶关联函数对所获得的光强信息进行关联计算，从而重构待测物体的空间信息。相比于传统成像，它有很多优势，例如，它可以实现无透镜成像［1］、遮挡物成像［2］，甚至在大气湍流和散射介质中也可以成像［3-4］，因此，在光学研究领域受到广泛关注。

鬼成像的理论实现思路最早由Klyshko 提出［5］。1995 年，Pittman 等人［6］第一次在实验上实现了纠缠光的关联成像，这也标志着鬼成像的正式诞生。2002 年，Bennink 等人［7］利用经典光源实现了鬼成像，从而证明了没有量子纠缠性质的经典光源也可以实现鬼成像。2004 年，Gatti 等人［8］提出了热光源鬼成像方案，2005 年Valencia等人［9］采用激光通过旋转毛玻璃的方式获得了赝热光源并且完成了赝热光源的鬼成像实验。2008 年，Shapiro［10］提出了计算鬼成像，2009 年，Bromberg 等人［11］验证了其可行性。然而GI 也存在局限性，热光GI 的能见度和信噪比很低，特别是对于复杂的灰度物体，而且瞬时GI 也不能像传统成像那么容易获得，需要进行大量的数据收集和处理。随着对鬼成像的更深入研究，人们对提高GI 成像质量提出了许多优化方案。例如归一化GI［11］、压缩GI［12］、高阶GI［13-17］、对应成像［18］等。虽然上述方案可以提高信噪比和能见度，但关于如何提高分辨率的论文很少，而分辨率同样是评价图像质量的重要指标。2016 年，Kuplicki 等人［19］采用非瑞利散斑作为光源进行GI，发现非瑞利散斑作为光源时可以获得更高的成像分辨率。此外，2022 年Zhao 等人［20］提出了二阶累积量GI 方案来提高成像分辨率，应用新的成像信息“二阶累积量”代替了原成像信息实现了更高的分辨率成像，并将该方案称为二阶累积量鬼成像（SCGI）。

本文通过非瑞利散斑场对SCGI 的成像信息进行优化，分析亚瑞利散斑对SCGI 成像信息的影响。发现亚瑞利散斑作为照明散斑时SCGI 成像结果要优于瑞利散斑SCGI 的成像结果。最后设计数值仿真，其仿真结果与理论分析相一致。

1 理论分析

鬼成像系统的原理图如图1 所示，选择一个可编程的先验光源作为成像系统的光源，在此系统中是应用数字微镜器件（DMD）生成的非相干光源，照明光在物体表面的强度分布可以通过计算的方式得到，同时透过物体的总光强可由桶探测器Dt测量获得。然后，通过二阶关联函数可得到待测物体的空间信息。

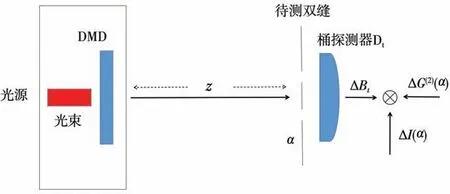
图1 鬼成像实验原理图

假设光源是波长为λ的单色光，光场从光源传播到物体的PSF 为h(x,α)。这里的x和α分别是源平面和物体平面的横向坐标。假设E(x)为源平面x处的光场，则物体平面的光场为：

物体平面的光强为：

式中，E*(α)是E(α)的复共轭。

如果T(α)代表的是光场透过物体的传递函数，那么通过桶探测器所收集的光强为：

那么GI 强度涨落二阶关联函数为：

式中，R为光源的直径；z为光源到待测物的距离；为系统的点扩展函数。它意味着对于一个类点物体，所得的像是个艾里斑，艾里斑第一能级的半径决定了成像分辨率，通常它等于PSF 的FWHM。

若考虑光源功率的扰动，则ΔG(2)(α)需要改成G(2)(I0,α)，根据文献［20］，此时系统的二阶累积量可以写为：

公式中：

根据公式（7）和公式（8）可知，κ2(α)的PSF是sinc4函数，因此SCGI 相比传统GI 具有更高的分辨率。此外可见，κ2(α)是ΔG(2)(I0,α)的涨落信息，因此，ΔG(2)(I0,α)的信息得到优化时，κ2(α)的信息也会随之被优化，进而可提升SCGI 的分辨率。而不同照明散斑的光场统计分布是不同的，导致ΔG(2)(α)中的光强涨落信息发生变化，这时ΔG(2)(I0,α)的信息会随之改变。这里，将采用非瑞利散斑场对ΔG(2)(I0,α)的信息进行优化，进而优化κ2(α)的信息。

首先，分析瑞利散斑和非瑞利散斑的统计特性，模拟出三种不同类型的散斑场，散斑场的特征是其光强的均方根对比度：

瑞利分布散斑场的均方根值C≈1，而非瑞利散斑场的均方根值C＞1 或者C＜1。C＞1 时为超瑞利散斑场，C＜1 时为亚瑞利散斑场，下面将生成三种不同类型的散斑场。

首先，利用计算机仿真将平面波经过相位均匀分布在0～2π 的随机相位调制器，生成瑞利散斑场ERay，如图2（a）所示。其次，使用Kuplicki［19］和Bromberg［21］中相同的方法，对瑞利散斑场ERay进行指数运算得到非瑞利散斑场E' =(ERay)n，其中当n＞1，n∈N*时，非瑞利散斑场E'为超瑞利散斑场Esuper-Ray，当0 ＜n＜1 时，非瑞利散斑场E'为亚瑞利散斑场Esub-Ray。

图2 瑞利散斑和非瑞利散斑的散斑图样

对比图2（a）和图2（b）可以清楚地看到超瑞利散斑颗粒之间的强度分布与瑞利散斑颗粒明显不同，超瑞利散斑颗粒有一些要比其他的亮得多。再对比图2（a）和图2（c）可以看到亚瑞利散斑颗粒之间的强度分布与瑞利散斑相比要更加均匀，这也是对比度较低的原因。

2 仿真模拟结果

为了更清楚地看到三种散斑场的统计特性对传统GI 的影响，分别用瑞利散斑和非瑞利散斑（亚瑞利、超瑞利）进行数值模拟。模拟条件：光源的波长为λ= 532 nm，光源直径R= 1 mm；光源到物体的传播距离z= 0.6 m；采样次数为100 000次，待测物体缝宽a= 0.9 mm；缝距b= 2.5 mm 的双缝，如图3 所示。瑞利散斑、超瑞利散斑、亚瑞利散斑成像结果如图4 所示。

图3 待测双缝

图4 照明散斑为瑞利散斑、超瑞利散斑、亚瑞利散斑时的传统GI 重构双缝图像

对比图4（a）～（c），可以清楚地看到在不考虑高阶关联，只用二阶关联去恢复待测双缝时，超瑞利散斑的效果是最模糊的，只能看到双缝的大概轮廓，双缝已经完全不能分辨。再对比图4（a）和图4（c）可以发现瑞利散斑能看到双缝，但双缝中间存在很多粘连部分，而亚瑞利散斑重构出的双缝明显粘连变少，可以更清晰地看到双缝，说明散斑颗粒之间的强度分布越均匀，越可以减少强度波动带来的影响，得到的成像结果会更好，同时也说明当非瑞利散斑作为照明散斑时，由于C＜1 或者C＞1 导致散斑场的统计特性发生改变，不再服从瑞利分布，这也使得公式中的ΔI(α)产生变化，从而使ΔG(2)(α)的信息发生改变。对比图4（b）、图4（c）可以发现，当C＜1 时的亚瑞利散斑场统计特性是可以优化ΔG(2)(α)的信息，而C＞1 的超瑞利散斑场统计性质没有对ΔG(2)(α)的信息产生更好的优化。因此，在接下来的工作中，将会讨论在SCGI的基础上，亚瑞利散斑的统计特性对ΔG(2)(α)的影响和对κ2(α)的影响。

针对上述理论推导结果进行相应的仿真模拟分析，以便于给出直观的结论。根据图1 所示的光学系统，选取的参数与上述参数相同，这里依旧选取图3 作为待测物体。数值仿真结果如图5 所示。

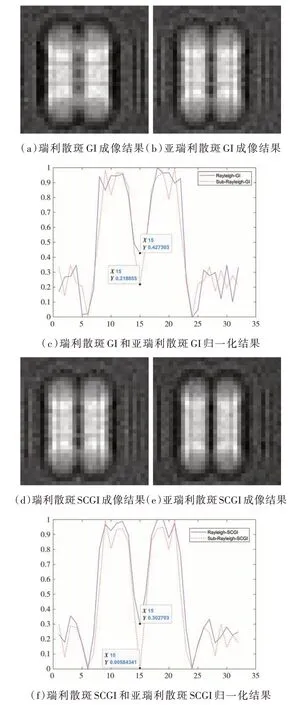
图5 缝宽a = 0.9 mm，缝距b = 2.5 mm，z = 0.6 m 时的仿真结果

图5（a）、图5（b）、图5（d）、图5（e）分别给出了瑞利散斑GI、亚瑞利散斑GI、瑞利散斑SCGI和亚瑞利散斑SCGI 的成像结果。图5（c）和图5（f）分别是图5（a）、图5（b）和图5（d）、图5（e）的归一化截面图。对比图5（c）、图5（f）可以看出瑞利散斑SCGI 和亚瑞利散斑GI 的中心凹陷分别为0.302 和0.218，成像分辨率相差并不大，但都要优于瑞利散斑GI 的分辨率。而亚瑞利散斑SCGI 中心凹陷却是0.006，可以看到亚瑞利散斑SCGI 的分辨率要明显优于亚瑞利散斑GI 和瑞利散斑GI。最后对比图5（d）～（f）发现亚瑞利散斑SCGI 的成像分辨率同样优于瑞利散斑SCGI。通过对图5（a）～（f）的对比发现，基于亚瑞利散斑SCGI 的分辨率是四种成像方案中最好的。

以上的仿真结果表明，用亚瑞利散斑作为SCGI 系统照明散斑时，亚瑞利散斑场的统计特性对κ2(α)信息的影响要大于它对ΔG(2)(α)信息的影响，用亚瑞利散斑作为SCGI 系统照明散斑，可以优化κ2(α)的信息，得到比传统瑞利散斑SCGI 更好的分辨率。数值仿真结果与之前的理论分析相一致，验证了方法的正确性。

3 结论

应用亚瑞利散斑对光场进行了波前调制，通过研究发现亚瑞利散斑场统计特性的改变，导致光强的涨落信息发生变化，进而优化了κ2(α)的信息，提升了传统瑞利散斑SCGI 的分辨率。并且，通过数值仿真对理论分析结果进行验证，证明了所提出方法的正确性。综上，可以通过高阶的亚瑞利散斑场对κ2(α)的信息进行更进一步的优化，进而更进一步地提升SCGI 的分辨率。