基于Hopkinson杆试验技术的PA-GF50复合材料动态力学行为

王严培， 姜启帆， 李玉龙

(西北工业大学 航空学院, 陕西 西安 710072)

0 引言

短玻璃纤维增强聚酰胺复合材料，是以无机短玻璃纤维(GF)为增强材料、热塑性聚酰胺(PA)材料为基体的复合材料。PA材料作为广泛应用的工程塑料，具有优良的力学性能、自润滑性、耐磨性等特性；GF材料则具有拉伸强度高、化学稳定性好、耐高温、电绝缘等良好性能，而且还能通过表面化学处理提高与树脂的界面粘结力，进一步改善相关力学性能。集合两者特性的短玻璃纤维增强聚酰胺复合材料的性能备受关注。

Frihi等[1]研究了材料制备冷却速度和短玻璃纤维含量对材料组成成分和性能的影响。Chebbi等[2]建立了PA-GF材料的各向异性超弹性本构模型。Horst等[3]研究了PA-GF30的孔隙和界面对材料疲劳破坏机制的影响。O’Regan等[4]比较了多种利用混合法则预测PA-GF材料杨氏模量的方法。Thomason[5]研究了纤维的强度、长度和组织形式对材料性能的影响。Hassan等[6]认为随纤维长度的提高，PA-GF材料的强度和模量提高，但材料失效应变降低。王艇[7]考察了纤维含量从0%到50%的短玻璃纤维增强聚酰胺复合材料的性能，通过试验证明纤维含量30%时，拉伸强度和模量达到最大值，之后随纤维含量的提高而有所降低。Gocek等[8]通过对不同纤维含量材料的拉伸试样断口的扫描电子显微镜(SEM)分析认为，随纤维含量的提高，材料的主要破坏模式由纤维拔出转化为纤维断裂。Ibáez-Gutiérrez等[9]的研究表明，随纤维含量的提高(从0%提高到50%)，PA-GF材料的缺口试样强度持续提高。一般认为，随纤维含量提高，材料脆性特征明显，压缩强度提高，拉伸强度先提高、后降低[10]。Benaceur等[11]通过试验研究了多应变率下聚酰胺的强度和流动应力，结果表明，材料流动应力是应变率对数的双线性函数，材料随应变率提高而增强。Mouhmid等[12]通过试验测定了加入0%、15%、30%、50%短玻璃纤维的PA在准静态载荷下的应变率效应和破坏形式，认为加入30%、50%短玻璃纤维的材料损伤由基体塑性、微裂纹扩展、纤维拔出和断裂决定。由于基体[11]和纤维本身存在正相关的应变率效应[13]，玻璃纤维增强聚酰胺复合材料的应变率效应，尤其是在准静态和动态加载时的应变率效应尚不明确。

作为一种广泛应用的工程材料，PA-GF复合材料的配比以及制备工艺、准静态力学性能等都有比较成熟的理论和测试体系[14]，但其多应变率下材料力学特性研究较少，尤其是动态力学性能研究数据不足以支撑包含冲击载荷的设计需要。PA-GF复合材料尤其是纤维含量较高(50%)材料的动态力学性能很有研究的必要。

本文对纤维含量50%短玻璃纤维增强聚酰胺复合材料进行了多个应变率(0.000 5～1 600 s-1)下的压缩、拉伸试验，定量确定了材料的应变率效应，并对材料动态加载下的变形破坏机理进行了讨论。

1 试验方法

1.1 材料制备和试样尺寸

PA-GF50材料为添加50%短玻璃纤维增强的聚酰胺基复合材料，材料本身呈现黑色，质脆。

PA经80 ℃真空干燥箱恒温干燥12 h后，用10%偶联剂KH50对短玻璃纤维进行表面处理,混合均匀后通过双螺杆挤出机造粒，挤出机各段温度为220 ℃左右，机头温度为215 ℃. 制备的共混粒料在鼓风干燥箱于80 ℃干燥12 h，然后注塑成复合材料板材。板材由广鹏实业塑胶有限公司提供。经机械加工成为试验需要的试样，压缩和拉伸试样轴向与注塑方向一致。短玻璃纤维长度为10～60 μm，平均纤维长度为20 μm. 压缩试验试样尺寸为φ10 mm×10 mm 和φ6 mm×6 mm两种；拉伸试样尺寸为哑铃状试样，厚度为3 mm，试样形状如图1所示。

图1 拉伸试样尺寸Fig.1 Tensile specimen

1.2 加载设备

准静态液压试验机根据载荷范围选用10 t电子万能试验机。动态试验在SHPB和SHTB上进行，设备简图如图2和图3所示。

图2 SHPB系统Fig.2 SHPB setup

图3 SHTB系统Fig.3 SHTB setup

图2所示为SHPB系统，波导杆材料为马氏体时效钢，波速c0=4 816 m/s，杨氏模量E=186.55 GPa，长度均为1 000 mm. 图3所示为SHTB系统，波导杆材料为铝合金，波速c0=5 198 m/s，杨氏模量E=76.26 GPa，长度均为900 mm. 为实现应力平衡和近似恒应变率加载，压杆和拉杆均应用了薄铝片波形整形器，其中，压杆整形器尺寸为φ3 mm×1 mm、拉杆整形器为均匀分布在子弹导轨末端法兰盘上的3个φ4 mm×1 mm的薄铝片。

1.3 测量方法

准静态试验通过试验机的机器位移和力传感器得到应力- 应变曲线。根据一维应力波理论，通过贴在波导杆上应变片测得的反射波和透射波应变历程，得到试样的应力- 应变历程[15]：

(1)

图4 典型曲线Fig.4 Typical curves

式中：As、ls分别表示试样加载面面积和标距段长度；Ab、Eb分别表示波导杆截面积、弹性模量；εr、εt为波导杆上应变片测得的反射波和透射波应变。图4所示为典型原始波形曲线。

为保证试验精度，压缩试样保证加载方向两个表面平行度精度在微米级，两波导杆、准静态试验机带万向头的压头对中良好，压缩试验中试件和压头之间加润滑剂，润滑剂摩擦系数为0.02，结合材料失效应变很小(约6%)，试件和压头之间的摩擦可忽略不计。拉伸试样保证波导杆、准静态试验机拉伸夹具对中良好的基础上，确保试样与波导杆粘接牢固且平行度良好，并保证试样在标距段断裂，以此获得有效数据。

2 试验结果

2.1 应力平衡校验

SHPB和SHTB测试过程中，保证试验有效性的一个重要条件[16-17]是加载过程中试样达到应力平衡。对于PA-GF50材料，由于其在准静态加载下的失效应变较小，材料呈现较为明显的脆性特征，因此动态加载条件下的应力平衡校验不可缺少[17]。通常，判断试样在试验中是否达到应力平衡时可引入应力均匀系数：

(2)

式中：σI(t)、σT(t)分别为试样与波导杆接触处波导杆上的应力。图5所示为应力平衡校验典型结果，图中可以看出，在α(t)=0.05时，试样还远未达到破坏点，可见，在整个加载过程中，试样的应力平衡得到了保证。

图6为根据图4、图5典型结果得到的材料真实应力- 应变、应变率- 应变曲线。由图6(a)、图6(b)两图可以看出，应变率在试样较小应变(0.015和0.010)时达到近似恒定应变率，并持续到试样失效，故可以认为，试验有效。

2.2 试验结果

考虑到材料的分散性、试验的随机误差，为真实反映材料本身力学性能，每种加载方式均进行了5～8次试验，保证有效数据有5个及以上的重复性。

压缩试验分别在准静态液压试验机、SHPB上进行，结果如表1、图7(a)所示。材料在0.005 s-1应变率下强度增强很少，在400 s-1、900 s-1和1 600 s-1应变率下分别增强31.00%、25.00%和29.00%，即材料在400 s-1应变率下强度达到最大值，增大应变率，材料强度降低。材料失效应变动态加载下为3.5%，准静态加载下为4.5%.

图5 应力平衡校验Fig.5 Stress equilibrium

图6 典型应力- 应变曲线Fig.6 Typical stress-strain curves

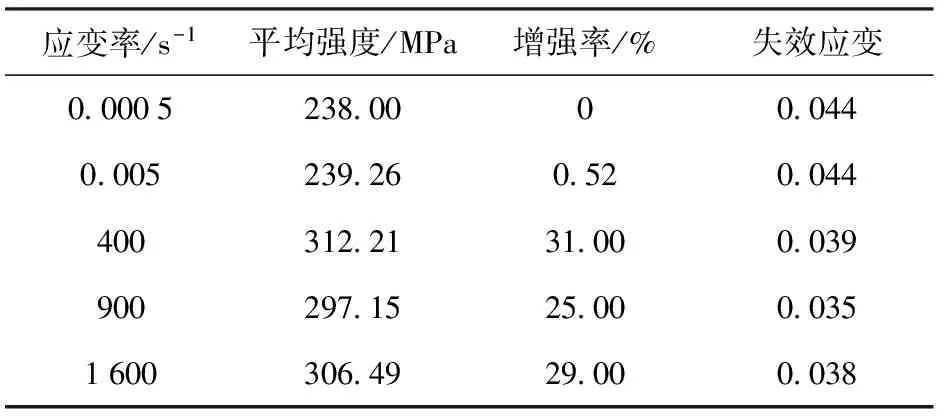
表1 平均压缩结果

图7 典型多应变率应力- 应变曲线Fig.7 Typical stress-strain curves at multiple strain rates

拉伸试验分别在准静态液压试验机、SHTB上进行，结果如表2、图7(b)所示。材料在0.005 s-1应变率下强度增强12%，与Cuvalci等[18]、Ibanezgu-tierrez等[9]、Mouhmid等[19]试验结果一致(见图8)，在400 s-1、800 s-1和1 200 s-1应变率下分别增强46.0%、47.0%和28.0%，即材料在800 s-1应变率下强度达到最大值之后，增大应变率，材料强度降低。材料失效应变动态加载下为4.0%，准静态加载为8.0%左右。材料的模量随应变率增大有明显增大的趋势，并在动态载荷下保持稳定，但材料在准静态和动态载荷下强度区分明显。材料失效应变拉伸和压缩加载下没有显著区别，动态加载下为3.5%～4.0%，准静态加载下略大。

表2 平均拉伸结果

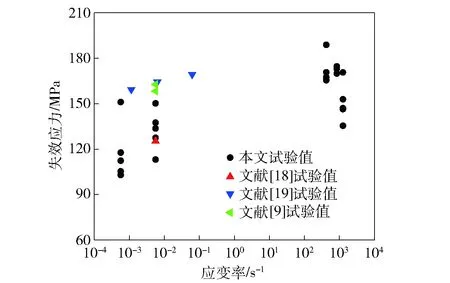
图8 拉伸试验结果Fig.8 Results of tension experiments

3 试验结果分析

3.1 应力- 应变曲线分析

由于短玻璃纤维材料结构的复杂性，材料力学性能表征困难，通过材料应力- 应变曲线可部分预测材料变形和失效特征及过程。图9所示为典型试样表面的SEM图。

图9 试样表面SEM图像Fig.9 Microscopic characterization of specimens

压缩典型应力- 应变曲线见图10(a)和图10(b)。准静态载荷下材料变形过程可分为如图10(a)所示5个阶段：1)预加载阶段，材料中可能存在的孔隙压实阶段；2)弹性变形阶段；3)伪塑性阶段，材料中微裂纹成核扩展阶段；4)流动段，微裂纹稳定扩展阶段；5)失效阶段，微裂纹扩展组合成为宏观裂纹，材料失效。动态载荷下材料变形过程可分为4个阶段：1)预加载阶段，试样中可能存在的孔隙压实，试样应变率随应变逐步提高；2)弹性变形阶段，应变率提高至稳定值后保持不变；3)伪塑性阶段，材料模量逐渐减小，试样中微裂纹成核扩展；4)失效阶段，微裂纹迅速扩展成宏观裂纹，试样失效。

值得注意的是，比较准静态和动态压缩加载条件下应力- 应变曲线，二者均存在预加载阶段、弹性变形阶段、伪塑性阶段和最后的失效阶段，且从预加载阶段到伪塑性阶段二者经历的应变几乎相同(0.032、0.036)。动态加载与准静态加载相比仅缺少了材料达到强度极限之后经历的流动段，在压缩载荷下，动态加载条件改变了材料的变形破坏机制。

拉伸典型应力- 应变曲线见图10(c)和图10(d)。比较两条曲线，可以看出拉伸加载条件下，材料变形和失效过程基本分为3个阶段：1)预加载阶段，准静态表现为曲线斜率较大，动态曲线在此阶段未达到恒定应变率；2)弹性变形阶段；3)伪塑性、失效阶段，拉伸载荷下伪塑性阶段较短，试样失效较压缩载荷下快。Horst等[3,20]也认为PA-GF材料的失效过程为：材料先从短纤维末端产生孔隙，孔隙扩展成为微裂纹，准静态载荷下微裂纹互相连接形成宏观裂纹，与对材料拉伸变形过程的分析类似。

3.2 材料变形和失效过程分析

材料动态加载下和准静态加载下的力学破坏机理不同。Selmi等[21]认为，纤维和基体之间的界面层是导致流动塑性段出现的原因。动态加载条件下可能改变了界面层中微裂纹传播的方式。综合断口SEM特征(见图11)，比较图11(a)、图11(b)，材料在准静态加载条件下，微裂纹扩展阶段有足够的时间组合形成宏观裂纹，故断口较为平整，动态载荷下微裂纹扩展组合不充分，微裂纹独立扩展，形成纤维拔出、纤维断裂等特征。比较图11(c)、图11(d)，准静态拉伸载荷下，孔隙形成的微裂纹扩展充分，纤维拔出明显，而动态拉伸载荷下，微裂纹扩展不充分，纤维拔出较难，主要表现为纤维断裂。

图10 典型应力应变曲线Fig.10 Typical stress-strain curves

图11 典型断口SEM图Fig.11 SEM micrographs of typical fractured specimens

材料在压缩和拉伸载荷作用下的破坏模式不同。比较图10(a)、图10(c)，材料在准静态载荷下，拉伸强度只有压缩的52.0%；比较图10(b)、图10(d)，材料在动态载荷下，拉伸强度为压缩的64.0%. 比较宏观断口(见图12和图13)，发现材料在压缩载荷作用下材料为剪切破坏，拉伸载荷作用下为直接断裂。SEM图(见图11)也支持上述观点。

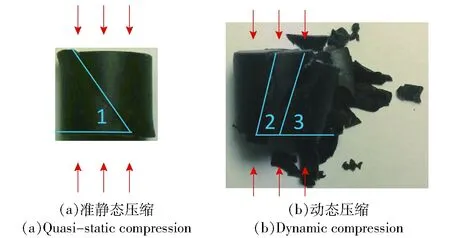
图12 压缩试样破坏宏观形貌Fig.12 Macro morphology of compressed specimen

图13 拉伸试样破坏宏观形貌Fig.13 Macro morphology of tensile specimen

3.3 应变率效应

从图14可以看出，随着应变率的提高，材料强度增强，失效应变降低，符合分析比较准静态和动态加载下应力应变曲线得到的结论。准静态载荷下和Mouhmid等[19]结果类似，且均体现出PA-GF材料在准静态载荷下(应变率10-5～10-2s-1)应变率效应不显著的特点。试样破坏之后的形态见图12和图13所示，低应变率下试样未完全碎裂，表现为主裂纹贯穿试样破坏，主裂纹方向与加载方向夹角较大；而动态载荷下，试样碎裂得比较彻底，裂纹方向与加载方向夹角较小，Chen等[22]在碳纤维材料中也观察到了动态载荷下试样宏观裂纹方向与加载方向夹角较小的现象。在应变率提高之后，材料中存在的微裂纹成核扩展，但由于应变时间短，相互之间不能有效组合，故分别扩展成为宏观裂纹，表现为多宏观裂纹的损伤，试样碎裂比较彻底。同时，准静态载荷下，微裂纹互相组合成为主裂纹破坏的过程吸收的能量较碎裂形式吸收的能量少，表现为准静态载荷下的材料强度低于动态载荷。另外，从图14可以明显看出，压缩载荷下，材料在400 s-1应变率下达到了类似于转变应变率的状态，拉伸载荷下，材料在800 s-1应变率下达到此状态，在此状态下，材料强度达到最大，失效应变也达到较大的状态，之后随着应变率的继续增大，材料强度有所降低。

图14 应变率效应曲线Fig.14 Strain rate effect curves

4 结论

本文通过准静态、动态以及拉伸、压缩加载条件下的试验，得到PA-GF50材料的力学性能及失效破坏特征如下：

1)材料应变率效应较为明显，材料动态载荷下呈现较为明显的脆性破坏特征，表现为动态载荷下强度提高、失效应变减小。压缩载荷下材料在400 s-1、900 s-1和1 600 s-1应变率下分别较准静态载荷下增强31%、25%和29%；拉伸载荷下材料在400 s-1、800 s-1和1 200 s-1应变率下分别较准静态载荷下增强46%、47%和28%. 材料失效应变动态加载下压缩为3.5%，准静态载荷下为4.5%；拉伸情况下，动态为4.0%，准静态为8.0%左右。材料动态加载条件下失效应变显著减小，试验后的试样破坏形态也显示了这一特征。

2)材料在压缩和拉伸载荷作用下的破坏模式不同，压缩载荷作用下材料为剪切破坏，拉伸载荷作用下为直接断裂。材料失效应变拉伸和压缩加载下没有显著区别，动态载荷下为3.5%～4.0%，准静态载荷下略大；材料拉伸强度为120～150 MPa，压缩强度为240～310 MPa之间，压缩强度约为拉伸的两倍。

3)材料动态加载下和静态加载下的力学破坏机理不同。静态加载下材料中存在的缺陷或加载过程中产生的微裂纹扩展过程中会相互组合形成宏观裂纹，断口整齐；而动态加载下微裂纹独立扩展成为宏观裂纹。

)

[1] Frihi D, Layachi A, Gherib S, et al. Crystallization of glass-fiber-reinforced polyamide 66 composites: influence of glass-fiber content and cooling rate[J]. Composites Science & Technology, 2016, 130:70-77.

[2] Chebbi E, Wali M, Dammak F. An anisotropic hyperelastic constitutive model for short glass fiber-reinforced polyamide[J]. International Journal of Engineering Science, 2016, 106:262-272.

[3] Horst J J, Salienko N V, Spoormaker J L. Fibre-matrix debonding stress analysis for short fibre-reinforced materials with matrix plasticity, finite element modelling and experimental verification[J]. Composites Part A: Applied Science and Manufacturing, 1998, 29(5/6): 525-531.

[4] O’regan M D F, Akay, Meenan B. A comparison of Young’s modulus predictions in fibre-reinforced-polyamide injection mouldings[J]. Composites Science and Technology, 1999, 59(3): 419-427.

[5] Thomason J L. The influence of fibre properties of the performance of glass-fibre-reinforced polyamide 6,6[J]. Composites Science and Technology, 1999, 59(16): 2315-2328.

[6] Hassan A, Yahya R, Yahaya A H, et al. Tensile, impact and fiber length properties of injection-molded short and long glass fiber-reinforced polyamide 6,6 composites[J]. Journal of Reinforced Plastics and Composites, 2004, 23(9): 969-986.

[7] 王艇. 玻璃纤维增强聚酰胺性能的研究[J]. 化工技术与开发, 2010, 39(2):18-20.

WANG Ting. Performance study of glass fiber reinforced polyamide[J]. Technology & Development of Chemical Industry, 2010, 39(2):18-20. (in Chinese)

[8] Gocek I, Keskin R, Ozkoc G. Effect of fiber content on failure modes of glass fiber reinforced injection molded polyamide 66 composites[J]. Advanced Materials Research, 2015, 1119:296-300.

[10] Chaichanawong J, Thongchuea C, Areerat S. Effect of moisture on the mechanical properties of glass fiber reinforced polyamide composites[J]. Advanced Powder Technology, 2016, 27(3): 898-902.

[11] Brunbauer J, Mösenbacher A, Guster C, et al. Fundamental influences on quasistatic and cyclic material behavior of short glass fiber reinforced polyamide illustrated on microscopic scale[J]. Journal of Applied Polymer Science, 2014, 131(19):5829-5836.

[12] Njuguna J, Mouti Z, Westwood K. Toughening mechanisms for glass fiber-reinforced polyamide composites[M]∥Qin Q H, Ye J Q. Toughening Mechanisms in Composite Materials. Cambridge, UK: Woodhead Publishing, 2015:211-232.

[13] Wu S H, Wang F Y, Ma C C M, et al. Mechanical, thermal and morphological properties of glass fiber and carbon fiber reinforced polyamide-6 and polyamide-6/clay nanocomposites[J]. Materials Letters, 2001, 49(6): 327-333.

[14] Benaceur I, Othman R, Guegan P, et al. Sensitivity of the flow stress of nylon 6 and nylon 66 to strain-rate[J]. International Journal of Modern Physics B, 2008, 22(9/10/11): 1249-1254.

[15] Mouhmid B, Imad A, Benseddiq N, et al. An experimental analysis of fracture mechanisms of short glass fibre reinforced polyamide 6,6 (SGFR-PA66)[J]. Composites Science and Technology, 2009, 69(15/16): 2521-2526.

[16] Ravichandran G, Subhash G. Critical appraisal of limiting strain rates for compression testing of ceramics in a split Hopkinson pressure bar[J]. Journal of the American Ceramic Society, 1994, 77(1):263-267.

[17] Suo T, Fan X, Hu G, et al. Compressive behavior of C/SiC composites over a wide range of strain rates and temperatures[J]. Carbon, 2013, 62(2):481-492.

[18] Cuvalci H, Erbay K, Ipek H. Investigation of the effect of glass fiber content on the mechanical properties of cast polyamide[J]. Arabian Journal for Science and Engineering, 2014, 39(12): 9049-9056.

[19] Mouhmid B, Imad A, Benseddiq N, et al. A study of the mechanical behaviour of a glass fibre reinforced polyamide 6,6: experimental investigation[J]. Polymer Testing, 2006, 25(4): 544-552.

[20] Horst J, Spoormaker J L. Fatigue fracture mechanisms and fractography of short-glass fibre-reinforced polyamide 6[J]. Journal of Materials Science, 1997, 32(14): 3641-3651.

[21] Selmi A, Doghri I, Adam L. Micromechanical simulations of biaxial yield, hardening and plastic flow in short glass fiber reinforced polyamide[J]. International Journal of Mechanical Sciences, 2011, 53(9): 696-706.

[22] Chen X, Li Y, Zhi Z, et al. The compressive and tensile behavior of a 0/90 C fiber woven composite at high strain rates[J]. Carbon, 2013, 61(5):97-104.