基于反向传播神经网络的陶瓷损伤参数反演分析

高玉波， 张伟, 李达诚， 宜晨虹, 汤铁钢

(1.中北大学 理学院, 山西 太原 030051; 2.哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150080; 3.中国工程物理研究院 流体物理研究所, 四川 绵阳 621900)

0 引言

陶瓷属于典型的弹脆性材料，部分陶瓷在冲击加载条件下会表现出一定的应变率效应和塑性特征，使得材料本构关系变得复杂。这种复杂的本构关系根源在于陶瓷的破坏模式，即材料内部存在的微裂纹、微孔洞等。这些微观缺陷随加载压力的增加将出现成核、扩展、汇集等微观现象，最终导致材料崩溃。由此可见，陶瓷的破坏模式并不是一种瞬间的坍塌，而是微观缺陷引起的裂纹扩展而导致完全破碎的一个过程，也就是说陶瓷材料的破坏伴随着损伤累积。

目前，关于陶瓷本构关系的理论模型可由对损伤的定义来划分，主要有细观损伤模型和连续损伤模型两个方向，其中，最具代表性的细观损伤模型是Rajendran-Grove模型[1]。该模型基于细观力学理论，将材料内部的微裂纹加入到弹性常数的损伤累积计算过程，其中，微裂纹的损伤通过无量纲的裂纹密度和断裂力学中裂纹的生长和扩展定律表征。Addessio等[2]、Deshpande等[3]、Clayton等[4-5]均从陶瓷材料的微裂纹、晶格结构等方面入手建立了相应的材料强度随裂纹扩展的损伤演化模型。细观损伤模型比较接近材料真实的损伤累积过程，但模型的建立具有局限性，主要适用于材料的大应力应变加载条件，且模型复杂、参量较多。连续损伤模型不考虑陶瓷材料微观缺陷的发展过程，采用连续介质力学对材料的强度、损伤和状态方程以一种连续函数形式进行表征，如早期的Drucker-Prager模型[2]。Johnson等参考了Drucker-Prager模型中含损伤的屈服面演化理论，建立了材料强度随损伤累积的Johnson-Holmquist(JH)本构模型，如JH-I[6]、JH-II[7]和JHB[8]本构模型。JH本构模型主要包含压力相关的材料强度、损伤和断裂，材料膨胀和断裂后的强度，以及材料应变率效应。由于JH本构模型物理意义明确、应用简便，并易于有限元分析的实现，一经推出后便受到了相关工程领域广泛地使用。

但是，在冲击加载条件下，材料损伤累积发生于完整陶瓷临界至完全破碎的过程，且伴随体积膨胀效应，导致实验方式尚无法直接获得损伤参数值。目前，常规方法则主要以经验为主，即将仿真结果与平板撞击实验结果比对以粗略建立损伤模型[9-12]。人工神经网络参考了生物神经系统对信息的处理方式，通过计算机语言来建立数据处理模型。人工神经网络包含大量的人工神经元，神经元之间由权值相互连接，根据外界信息的输入可改变权值的大小，并对输入信息进行建模，最终解决实际问题。其中，反向传播(BP)神经网络则可解决线性不可分问题，是人工神经网络的核心部分，被广泛地用于逼近、回归、分类识别等领域[13]。因此，本文提出了一种基于BP神经网络建模完成对JH-II本构模型中损伤参数的反演方法。

1 JH-II本构模型

JH-II本构模型发展了Drucker的含损伤屈服面演化理论，建立了陶瓷强度随损伤积累而连续减小的对应关系。JH-II本构模型中认为，当材料的损伤累积发生时(对应损伤因子D>0)，材料的强度随着塑性应变的增加而逐渐出现劣化现象，如图1所示。图1中对静水压力p和等效应力σ做了无量纲化处理，分别为p*=p/pHEL，σ*=σ/σHEL，其中，pHEL和σHEL分别为Hugoniot弹性极限(HEL)状态下的静水压力和等效应力[10]，μ为材料的比容。

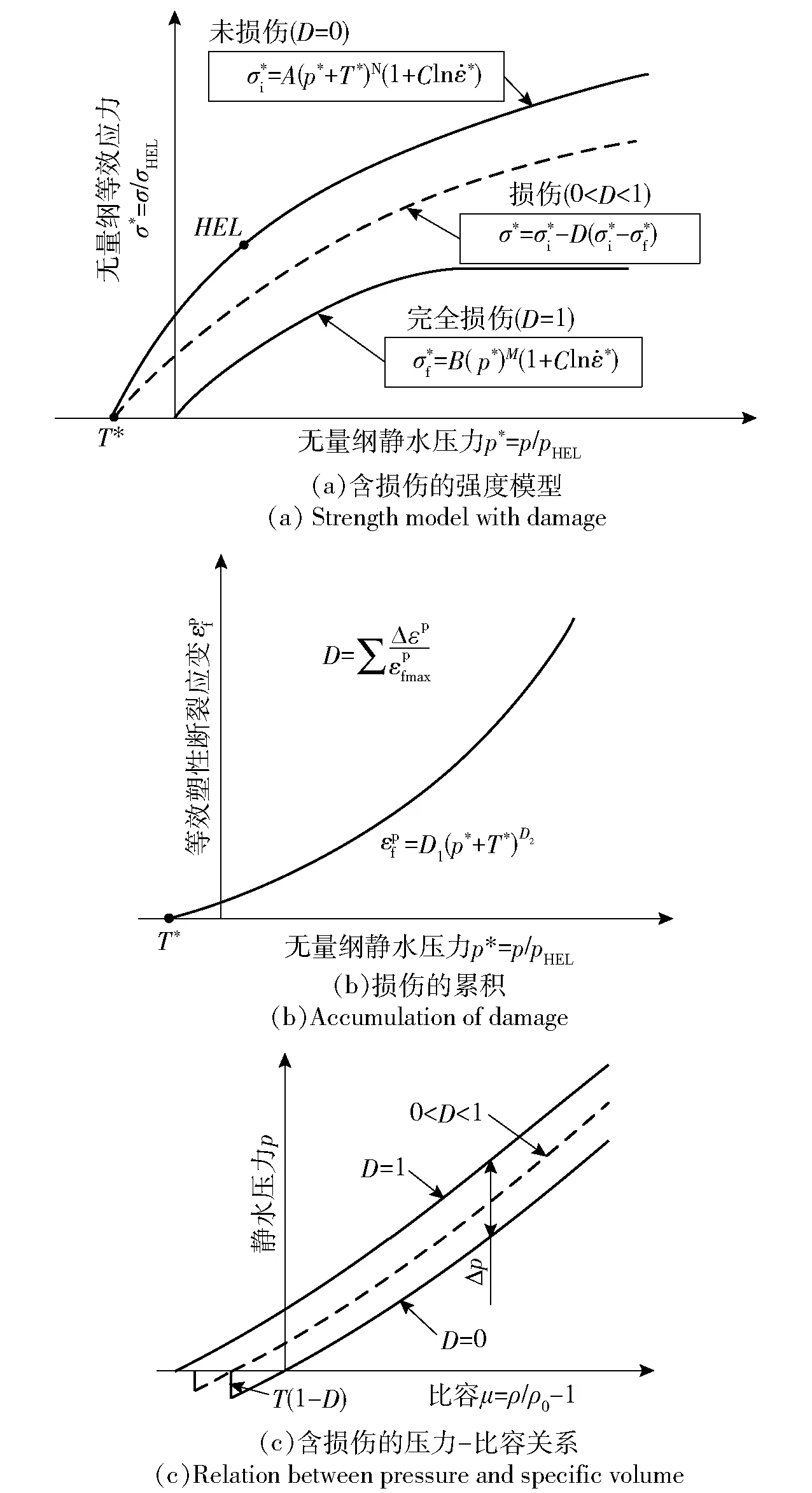
图1 JH-II本构模型Fig.1 Description of JH-II ceramic model

由图1所示，陶瓷材料的无量纲等效应力可描述为

(1)

在材料完整的情况下(未损伤，D=0)，无量纲等效应力为

(2)

在完全损伤情况下，无量纲等效应力为

(3)

在大应力应变条件下，JH-II本构模型中的材料损伤定义为损伤累积的形式：

(4)

图2 一定压力条件下陶瓷材料的强度、损伤和断裂示意图Fig.2 Strength, damage, and fracture of ceramic material at a constant pressure and strain rate

材料所能承受的最大的塑性应变可表示为

(5)

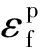
2 损伤参数反演

陶瓷JH-II本构模型中损伤参数的神经网络反演精度主要受两方面因素影响：BP网络的隐含层节点数和数值仿真建模。隐含层节点数需兼顾仿真工况数量、计算机性能和反演精度，可通过多次试算确定。数值仿真模型对反演结果的影响因素主要包括材料参数和模型网格，本文所取陶瓷材料参数由前期工作的实验和理论分析中获得并验证；而弹丸和陶瓷材料网格划分需要考虑弹靶接触引起的网格侵蚀，并适当选择网格大小。最终，反演精度可由BP神经网络的均方误差进行表征。

2.1 BP神经网络模型

BP神经网络的隐含层可以是多层的，并强调误差反向传播，如图3所示，图中ni为输入节点数，no为输出节点数。随着权值的不断训练，输出误差和目标输出误差的差值将逐渐减小，直到不再下降。其中，BP 神经网络的传递函数一般采用光滑可微的Sigmoid 函数，其自变量范围包含整个实数域。权值修改的方式为最速下降法的改进算法，例如动量BP 法、学习率可变的BP 算法、拟牛顿法、Levenberg-Marquard(LM)算法等。

图3 含两层隐含层的BP神经网络Fig.3 BP neural network with two hidden layers

本文采用MATLAB工具箱中改进的BP神经网络模块对样本进行训练，主要由输入层、隐含层和输出层构成。输入层包含两个节点，分别为侵彻深度和弹丸撞击速度；输出层的两个节点分别为待反演的损伤参数D1和D2. 隐含层和输出层的传递函数分别采用Sigmoid 函数和线性Purelin 函数。隐含层的节点数对网络性能有较大的影响，数量过少将导致计算不精确，相反则会导致计算时间过长。一般认为，隐含层的节点数nh与输入节点数ni和输出节点数no有关：

(6)

式中：a∈[0,10]；ni=1；no=2. 经过多次试算，nh取为3.

LM算法能够解决神经网络易于收敛于局部极小的缺点，其网络权值修正方式为

ω(n+1)=ω(n)-[JTJ+αJ]-1JTe，

(7)

式中：J为含误差性能函数的网络权值1阶导数的雅克比矩阵；α为比例系数，当α=0时，LM算法退化为牛顿法，当α取值无限大，(7)式相当于步长很小的梯度下降法；网络的误差e定义为

ej(n)=dj(n)-Yj(n)，

(8)

dj(n)和Yj(n)分别为网络的期望输出和实际输出，j为输出层单元数。

经过n次迭代后，网络的误差信号为

(9)

图4给出了BP神经网络流程图。首先，确定陶瓷类材料损伤参数D1和D2的取值范围，完成样本的设计；其次，采用AUTODYN有限元仿真软件完成不同取样点的数值仿真，并提取仿真中弹丸的侵彻深度；将仿真侵彻深度和弹丸撞击速度数据作为神经网络的输入，损伤参数D1和D2作为网络的输出，对网络进行训练；最后，将实验中获得的侵彻深度和弹丸撞击速度数据输入训练成型的网络模型，反演获得损伤参数。运算顺序角度上，BP神经网络对损伤参数的反演等同于数值仿真的逆运算，即将损伤、侵彻深度、撞击速度等参数的运算顺序反转，其本质是一种对参数和仿真结论之间的归纳算法。

图4 BP神经网络程序流程图Fig.4 Flow chart of BP neural network program

参考陶瓷类材料JH-II本构模型的损伤参数值[9-12]，假设TiB2-B4C 复合材料的D1取值范围在0.001～0.011之间，D2在0.5～2.1 之间[14]。在BP神经网络建模过程中，只考虑参数取值范围内样本点的均匀散布，D1和D2分别每隔0.002、0.2 取一个值。

2.2 侵彻深度实验

侵彻深度实验在哈尔滨工业大学高速撞击研究中心二级轻气炮装置上进行，弹丸采用φ8 mm钨合金球，密度为17.6 g/cm3，质量为4.82 g，撞击速度分别为1 717 m/s、1 877 m/s、2 025 m/s和2 220 m/s. 靶板为常用的陶瓷/金属复合装甲，其中，陶瓷面板为TiB2-B4C复合材料，尺寸为φ100 mm×10 mm，并增加铝合金侧向约束；金属背板为φ120 mm×50 mm的2A12铝合金，靶件示意图如图5所示。

图5 球弹丸撞击陶瓷/金属复合装甲示意图Fig.5 Schematic diagram of spherical projectile impacting on ceramic/metal composite armor

2.3 数值仿真

实际工况可简化为轴对称问题处理，采用AUTODYN仿真软件对钨合金球弹丸侵彻陶瓷/金属复合装甲进行二维和三维数值模拟建模。其中，二维仿真模型数据主要用于损伤参数的BP神经网络反演；三维模型主要用于验证陶瓷面板的完整损伤形态。二维模型中，弹丸和陶瓷面板均采用光滑粒子流体动力学方法(SPH)描述。铝合金背板和陶瓷侧向约束为Lagrange网格，并采用侵蚀法解决弹靶撞击过程中发生的网格畸变。模型中SPH粒子影响域半径和背板中心区域Lagrange网格均为0.2 mm，如图6(a)所示。三维模型中，所有材料均采用Lagrange网格，弹着点附近网格尺寸为0.4 mm，如图6(b)所示。

表1给出了TiB2-B4C复合材料的JH-II本构模型参数，λ为泊松比，ρ0为常温常压条件下材料的密度，E0为常温常压条件下材料的弹性模量，μHEL为Hugoniot弹性极限状态下的材料比容，K1为体积模量，K2、K3为材料常数，G为剪切模量，β为冲击波作用下材料内弹性能与静水压势能之间的能量转化率。其中，损伤参数根据BP神经网络的样本要求进行设计。钨合金和2A12铝合金均属于延性金属材料，仿真材料模型均采用Shock状态方程和Johnson-Cook本构关系进行描述[15-16]。

图6 有限元模型Fig.6 Finite element model

表1 TiB2-B4C复合材料的JH-II本构参数

2.4 模型训练和参数计算

图7 BP神经网络训练、验证和测试的均方误差Fig.7 MSEs of BP neural network in training, validation and test process

根据BP神经网络样本对损伤参数D1和D2的设计，仿真工况数量为216. 将仿真中80%、10%、10%的工况分别对神经网络进行训练、验证和测试，获得了3种状态下网络的均方误差约为0.08，如图7所示。

BP神经网络建模过程中，训练、验证和测试网络的相关系数分别为0.928 9、0.927 8和0.938 6，总的相关系数为0.928 1. 将侵彻深度实验中弹丸初始撞击速度v0和侵彻靶板深度P输入到训练好的网络模型，结果显示反演获得的D1和D2数据较为接近，如表2所示。将不同速度下神经网络反演获得的D1和D2取平均值，最终值分别确定为0.004 1和1.279 1.

表2 损伤参数D1和D2的反演结果

3 本构模型验证

陶瓷/金属复合装甲的侵彻深度和陶瓷面板的损伤是描述陶瓷复合装甲抗侵彻性能的重要指标。为了验证BP神经网络模型获得的TiB2-B4C复合材料损伤参数的有效性，将侵彻深度和实验回收的陶瓷面板损伤与数值仿真结果进行了对比，如图8和表3所示。由图8可知，数值仿真数据和实验数据吻合较好，正负误差在10%以内，说明JH-II本构模型的损伤参数能够较好地反映TiB2-B4C复合材料受高速撞击的力学响应特征。

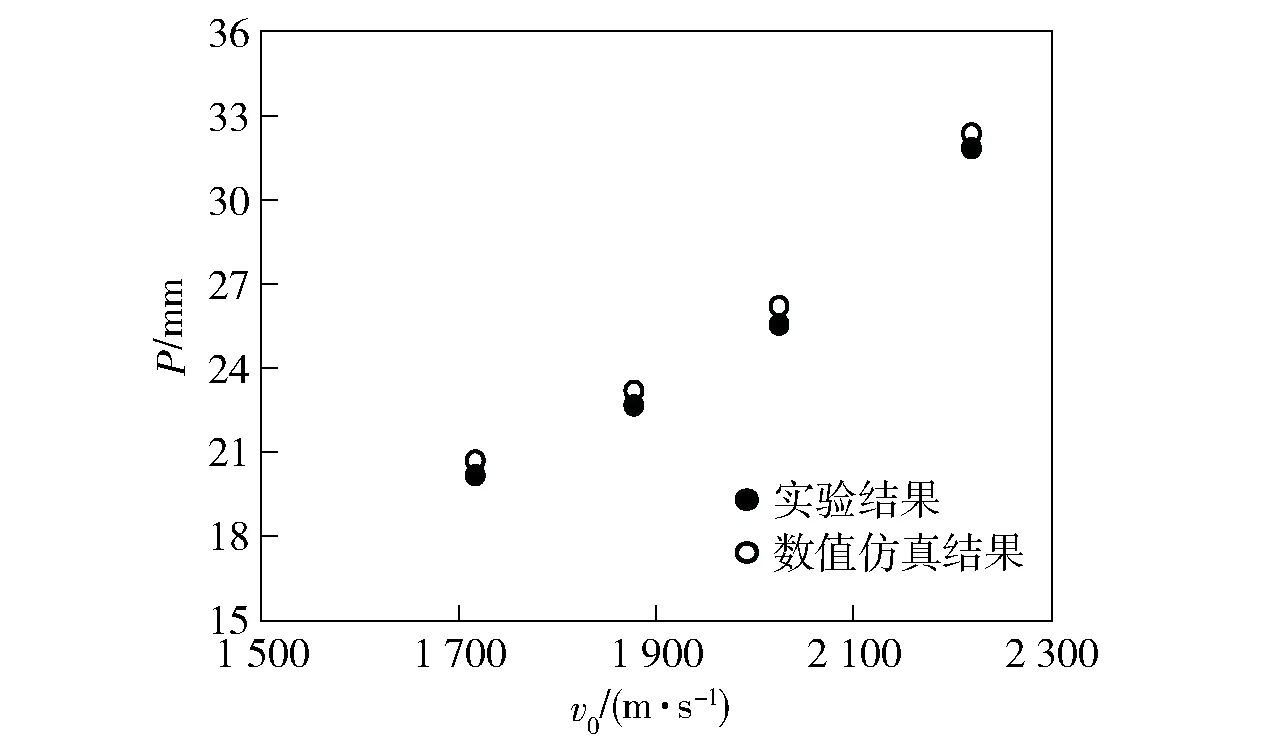
图8 实验和数值仿真侵彻深度对比Fig.8 Comparison of experimental and simulated penetrating depths

由表3可知，受到应力波的作用，整个陶瓷面板由于裂纹扩展和损伤演变发生了不同程度的破碎。实验结果表明，在弹着点附近的陶瓷呈颗粒或粉末状，说明陶瓷已处于完全损伤状态；远离弹着点，陶瓷的损伤可由环向裂纹和径向裂纹表征，且距离弹靶作用点越远，裂纹的密集程度越小，即陶瓷损伤程度越小。同时，由实验回收的陶瓷面板可知，在距离陶瓷板外圆15.2 mm处存在一个较为明显的环向裂纹；在数值仿真结果中，这个环向裂纹位置约为15.0 mm. 对于实验和数值仿真中的陶瓷面板径向裂纹，由于裂纹较为密集，具体位置较难给出定量值，但两者的陶瓷损伤形式接近。因此，数值仿真结果很好地再现了实验过程中陶瓷面板的裂纹扩展趋势，充分验证了所建立BP神经网络建模以及损伤参数反演的有效性。

4 结论

在冲击加载条件下，陶瓷材料的损伤累积伴随着体积膨胀效应，使得JH-II本构模型中损伤参数无法由实验方式直接获得。本文提出一种基于BP神经网络建模获得损伤参数的反演方法。

1)参考陶瓷类材料JH-II本构模型损伤参数取值，确定了反向传播神经网络中均匀分布的样本点。

2)采用侵彻实验和数值仿真相结合的方式完成了网络的建模以及损伤参数的反演。

3)对比实验回收的陶瓷面板破碎形貌和数值仿真数据，验证了建立的反向传播神经网络模型以及损伤参数反演的有效性。

)

[1] Grove D, Rajendran A. Overview of the Rajendran-Grove ceramic failure model[J]. Ceramic Transactions, 2002, 134:371-382.

[2] Addessio F L, Johnson J N. A constitutive model for the dynamic response of brittle materials[J]. Journal of Applied Physics, 1990, 67(7):3275-3286.

[3] Deshpande V, Evans A. Inelastic deformation and energy dissipation in ceramics: a mechanism-based constitutive model[J]. Journal of the Mechanics and Physics of Solids, 2008, 56(10):3077-3100.

[4] Clayton J D. Finite strain analysis of shock compression of brittle solids applied to titanium diboride[J]. International Journal of Impact Engineering, 2014, 73(11):56-65.

[5] Clayton J D, Tonge A L. A nonlinear anisotropic elastic-inelastic constitutive model for polycrystalline ceramics and minerals with application to boron carbide[J]. International Journal of Solids and Structures, 2015, 64/65:191-207.

[6] Meyers M A, Murr L E, Staudhammer K P. Shock-wave and high strain rate phenomena in materials[M]∥Johnson G R, Holmquist T J. A computational constitutive model for brittle materials subjected to large strains, high strain rates and high pressures. New York, NY, US: Marcel Dekker Inc, 1992: 1075-1081.

[7] Johnson G R, Holmquist T J. An improved computational constitutive model for brittle materials[J]. American Institute of Physics, 1994, 309(1): 981-984.

[8] Johnson G R, Holmquist T J, Beissel S R. Response of aluminum nitride (including a phase change) to large strains, high strain rates, and high pressures[J]. Journal of Applied Physics, 2003, 94(3): 1639-1646.

[9] Prakash A, Rajasankar J, Anandavalli N, et al. Influence of adhesive thickness on high velocity impact performance of ceramic/metal composite targets[J]. International Journal of Adhesion & Adhesives, 2013, 41(1):186-197.

[10] Johnson G R, Holmquist T J. Response of boron carbide subjected to large strains, high strain rates, and high pressures[J]. Journal of Applied Physics, 1999, 85(12):8060-8073.

[11] Hadavi V, Moreno C E, Papini M. Numerical and experimental analysis of particle fracture during solid particle erosion. Part I: modeling and experimental verification[J]. Wear, 2016, 356/357:135-145.

[12] Pawar M J, Patnaik A, Biswas S K, et al. Comparison of ballistic performances of Al2O3, and AlN ceramics[J]. International Journal of Impact Engineering, 2016, 98:42-51.

[13] Wang Z Y, Li P F. Dynamic failure and fracture mechanism in alumina ceramics: experimental observations and finite element modelling[J]. Ceramics International, 2015, 41(10):12763-12772.

[14] 杨震琦, 庞宝君, 王立闻, 等. JH-2模型及其在Al2O3陶瓷低速撞击数值模拟中的应用[J]. 爆炸与冲击, 2010, 30(5):463-471.

YANG Zhen-qi, PANG Bao-jun, WANG Li-wen,et al. JH-2 model and its application to numerical simulation on Al2O3ceramic under low-velocity impact[J]. Explosion and Shock Waves, 2010, 30(5):463-471. (in Chinese)

[15] Meyers M A. Dynamic behavior of materials [M]. New York, NY, US: John Wiley & Sons Inc, 1994.

[16] Cowper G R, Symonds P S. Strain-hardening and strain-rate effects in the impact loading of cantilever beams, technological report No.28 [R]. Providence, RI, US: Brown University, 1957.