基于数据配准的零件精密装配最佳接触状态研究

张体广， 张发平， 阎艳， 吴迪， 王戈， 郭少伟

(北京理工大学 机械与车辆学院, 北京 100081)

0 引言

形状误差是表面形貌误差的重要组成部分，是影响机械产品装配精度的关键因素之一。精密和超精密机械产品结构复杂，零部件的加工精度要求极高，其表面形状误差的几何分布通常是非均匀非对称的。如果以这类表面作为装配基准，即使不考虑装配力等引起的变形，不同的配合方式也将会使装配后的零部件形成不同的接触状态，产生不同的配合误差。而微小的误差将导致产品的性能急剧下降，从而影响整个系统的精度和性能。因此，在考虑形状误差的情况下，研究精密装配最佳接触状态对于实现装配精度预测、优化装配工艺、提高装配精度及稳定性具有重要意义。

形状误差可以用于判断加工后的零件是否合格，也是目前研究形状误差的主要方向，如文献[1-4]，而且还可以用于分析误差产生的原因。Grandjean等[5]在考虑与不考虑几何形状误差的情况下进行装配分析，研究表明零件配合表面的形状误差分布不同对装配精度的计算会出现偏差；张之敬等[6]提出一种面向装配的用熵函数来表征和评价零件的平面形状误差的方法；吕程等[7]采用小位移旋量理论进行公差的数学描述，建立了多公差耦合情况下零件平面误差变动的数学模型；唐水龙等[8]通过建立虚拟配合表面方法，将平面度容差分解成待装配零件沿装配方向的平动及其在参考坐标系中的转动进行了装配容差分析；左富昌等[9]采用差表面的方法提出一种形状误差与装配力共同作用下的配合表面接触状态分析方法，但此种方法只适用于平面。

目前研究几何形状误差对装配精度的影响中还存在以下问题：1)研究误差对装配精度影响主要集中在分析尺寸误差和位置误差对装配精度的影响，而忽略了形状误差对装配的影响；2)对于形状误差的研究主要集中在形状误差的评定方面，即把形状误差表达为一个公差标量值，当研究装配问题时都是将此标量数值作为尺寸误差的附加误差叠加到尺寸链中，这样将无法解决零件之间因装配表面的形状误差分布所形成的几何误差对装配精度影响的问题。为此，本文在考虑形状误差及其几何分布的情况下提出一种基于数据配准的实际配合表面接触分析与计算方法。首先分析形状误差的几何分布特性，定性揭示形状误差分布对装配精度具有不可忽略的影响；在此基础上基于数据配准方法提出配合表面接触点获取方法，并采用粒子群优化算法进行求解；基于接触点提出配合误差的计算方法；采用仿真实验通过对比考虑和不考虑形状误差分布对装配精度影响两种情况下的装配成功率，从统计意义上说明形状误差对精密刚度零件装配精度的影响不可忽视。

1 零件表面几何形状误差分布特性

现有的国际标准或国家标准中规定，形状误差是指被测提取要素对其拟合要素的变动量，其中，拟合要素的位置应符合国家标准GB/T1182—2008产品几何技术规范(GPS) 几何公差 形状、方向、位置和跳动公差标注规定的最小条件，即被测提取要素对其拟合要素的最大变动量为最小。形状误差值采用最小包容区域的宽度或直径来表征，最小包容区域是与形位公差带的形状、方向和位置相同、包容实际被测要素且具有最小宽度或直径的区域。如图1为平面度误差，即用两个平行的理想平面包容实际平面，两个理想平面之间的最小距离即为平面度误差。同样如圆柱面特征的几何形状误差包括：圆锥形、钟形口、沙漏形、桶形、香蕉形、凸角形和随机形状，如图2所示。

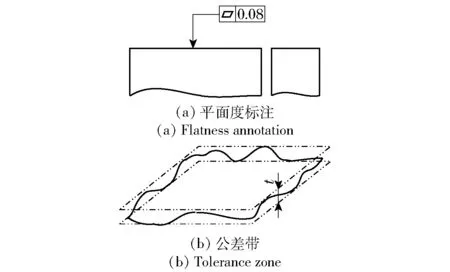
图1 平面度误差Fig.1 Flatness error

图2 圆柱面典型形状误差[10]Fig.2 Typical form errors of cylindrical shapes[10]

对于零件平面特征，采用平面度来表示形状误差的大小，而平面度Δ是一个标量值，无法表征实际加工平面高低起伏的变化，即表面形状误差几何分布特性。如图3所示，两个零件表面的平面度相同，但是形状误差几何分布情况却不同，如果以这两个零件为装配基准，则会导致两被装配零件实际接触面的空间几何位置发生不同变化，从而影响产品的装配精度[11]。因此，形状误差对精密零件的装配精度产生显著影响。

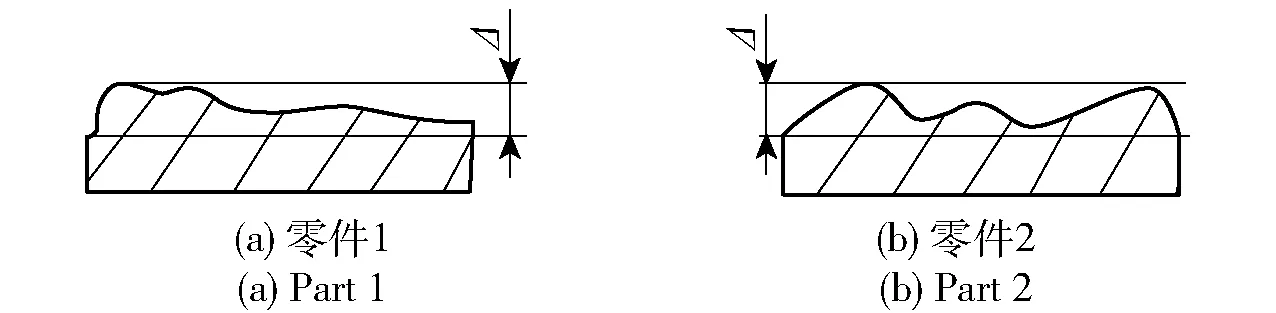
图3 几何形状误差分布特性Fig.3 Distribution characters of geometric form errors

对于精密刚度零件，由于形状误差的存在，两个零件装配时配合面之间是通过有限个点接触的，而非整个配合面完全接触。因此，当装配基准零件固定时，被装配零件的空间位姿取决于接触点的位置，而被装配零件的空间位姿决定了装配体的装配精度。进而，由于形状误差的传递与累积，导致形成系统的装配误差，最终体现在装配后整体系统的性能上。如图4所示，当零件配合表面存在形状误差时，图4(a)图表明平面度误差引起圆柱圆心的位置误差Δα，而图4(b)图说明平面度误差引起被装配体的方向误差Δβ[12].

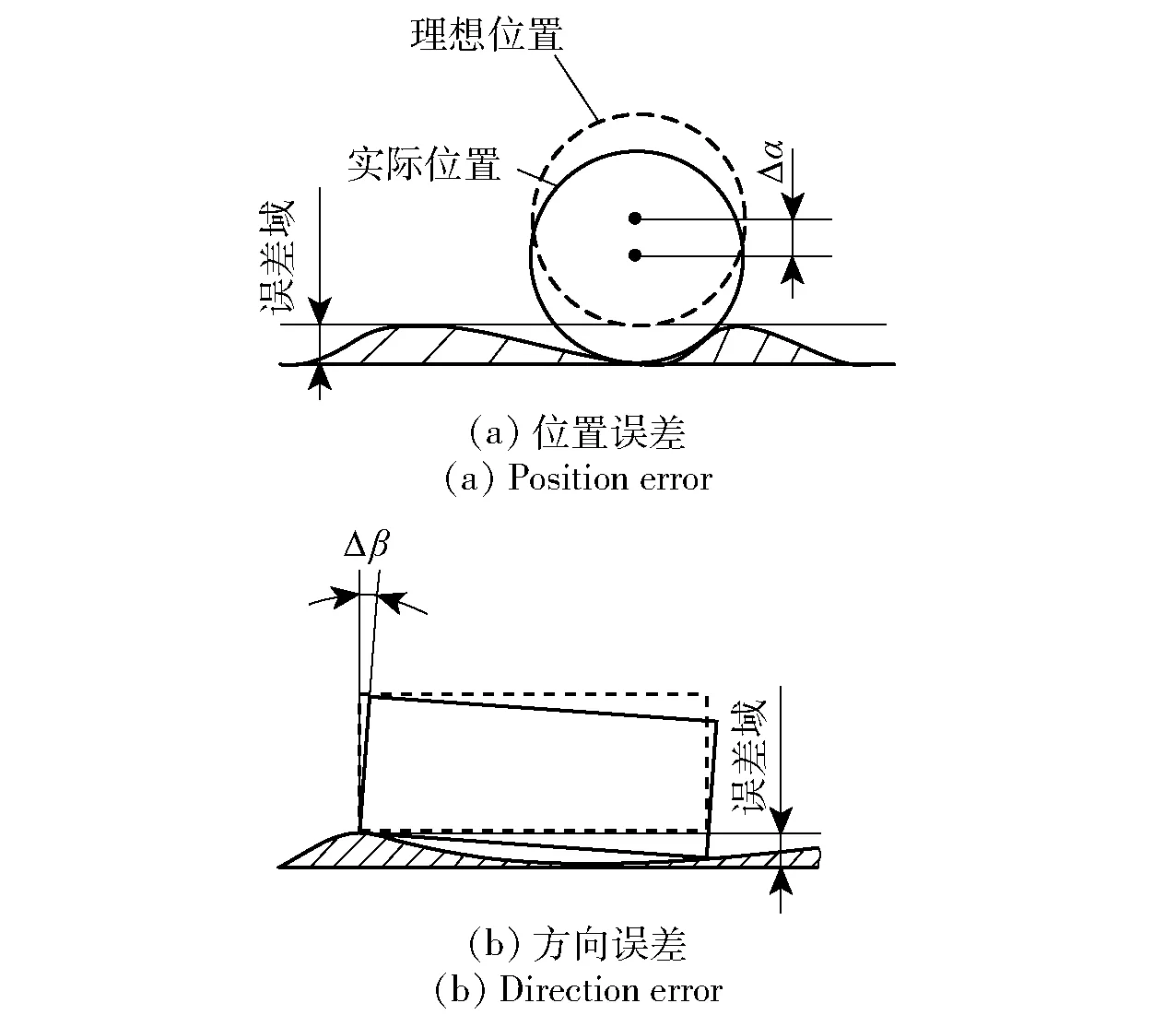
图4 形状误差导致的被装配零件位置与方向误差Fig.4 Position and direction errors caused by form errors

2 考虑几何形状误差的配合表面接触状态分析与建模

2.1 配合表面及其常见的配合表面形式

装配体的拓扑结构决定了各零件间的装配关系，零件依据装配关系通过几何表面的相互贴合完成装配，实现产品功能。配合表面或接触面是指由不同零件上的两个或两个以上的几何表面通过装配关系相互贴合形成的表面，根据组成配合面的常见几何元素类型可分为平面配合面、圆柱面配合面(孔、轴)、锥面配合面、球面配合面等，其中圆柱面配合有间隙配合、过盈配合、过渡配合，本文主要研究间隙配合的形式。根据配合面的接触形式又可以分为串联配合、同体并联配合、异体并联配合，如图5所示。图5中P1～P4表示零件，F1～F4表示配合表面。设计中常需要用装配关系来满足某些功能，本文以最常见的两配合面配合为对象，将常见的配合简化表达为如图6所示的几种形式。

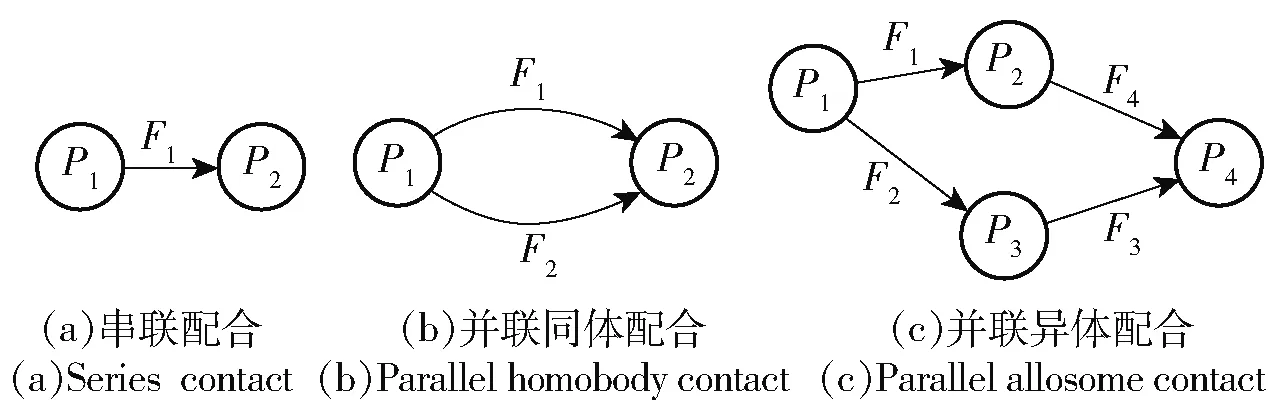
图5 串联、并联配合示意图Fig.5 Schematic diagram of series and parallel contact

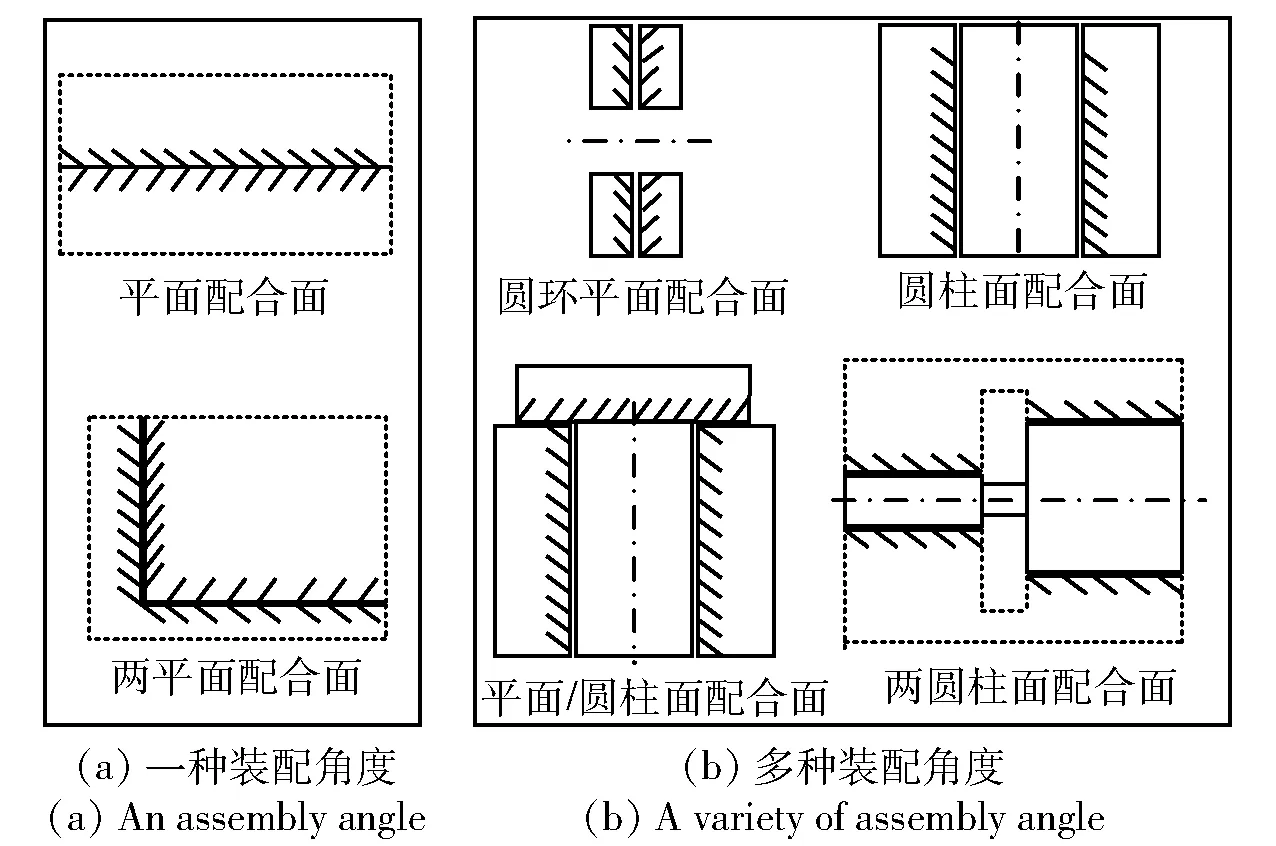
图6 常见配合表面形式Fig.6 Common forms of contact surface

2.2 基于数据配准的配合表面接触点获取方法

本文只针对高刚度精密零件，因此可以假设零件在装配过程中不发生变形，两个零件装配时配合面之间是通过有限个点接触的，如根据3点确定一个平面的基本理论，平面配合时视为3个接触点；圆柱面间隙配合时视为3点或者4点接触(视约束而定)。当确定了接触的位置后，就可以确定被装配零件的空间位姿，从而确定装配体的装配精度。

点云数据的配准是指通过坐标变换将不同角度获得的数据统一到同一个坐标系下，从而获得完整的三维模型点云数据。由于加工工艺(包括其他因素的影响)的不同造成两配合表面一定具有不同的几何特征，这与目前研究配准存在根本的不同(现有研究中要求匹配的曲面有相同曲面几何特征或曲面有相似的曲率)，最近点迭代(ICP)法，重复进行“确定对应关系点集——计算最优刚体变换”的过程，直到某个表示正确匹配的收敛准则得到了满足[13]，因此本文基于ICP法匹配进行改进，提出了基于改进ICP(IICP)法的接触点获取方法。

2.2.1 点云数据预处理

采用三坐标测量机测量两个装配零件的接触面，基于各自测量坐标系，在对数据进行过滤后，基准零件和被装配零件配合表面的测量数据表示如下：

(1)

(2)

(3)

(4)

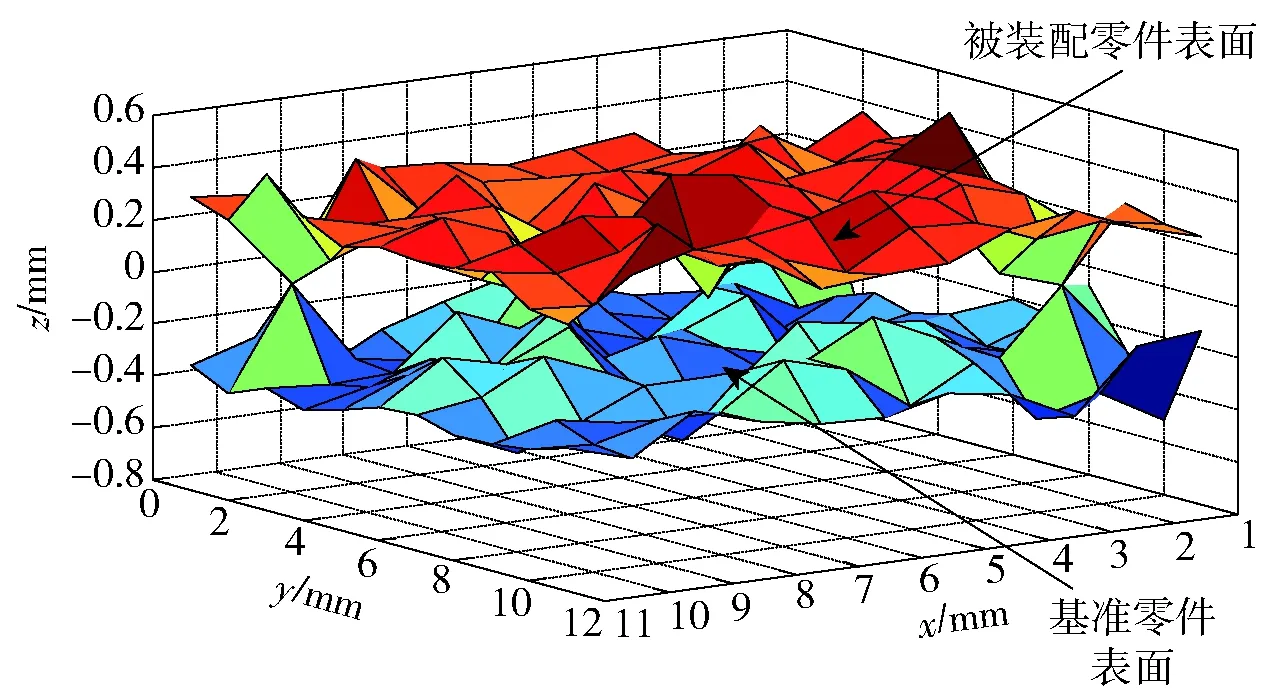
图7 公共坐标系下的两配合表面Fig.7 Contact surface under the same coordinate system

2.2.2 基于IICP的配合表面接触状态分析方法

零件的装配过程实质为把待装配零件从初始位置经过平移、旋转移动到基准零件上，并使两配合表面能够贴合，从而能够实现相应的功能。考虑形状误差的配合表面接触状态分析，通过采用数据配准的方法获取刚体坐标变换矩阵，计算待装配零件的最佳状态如图8所示。

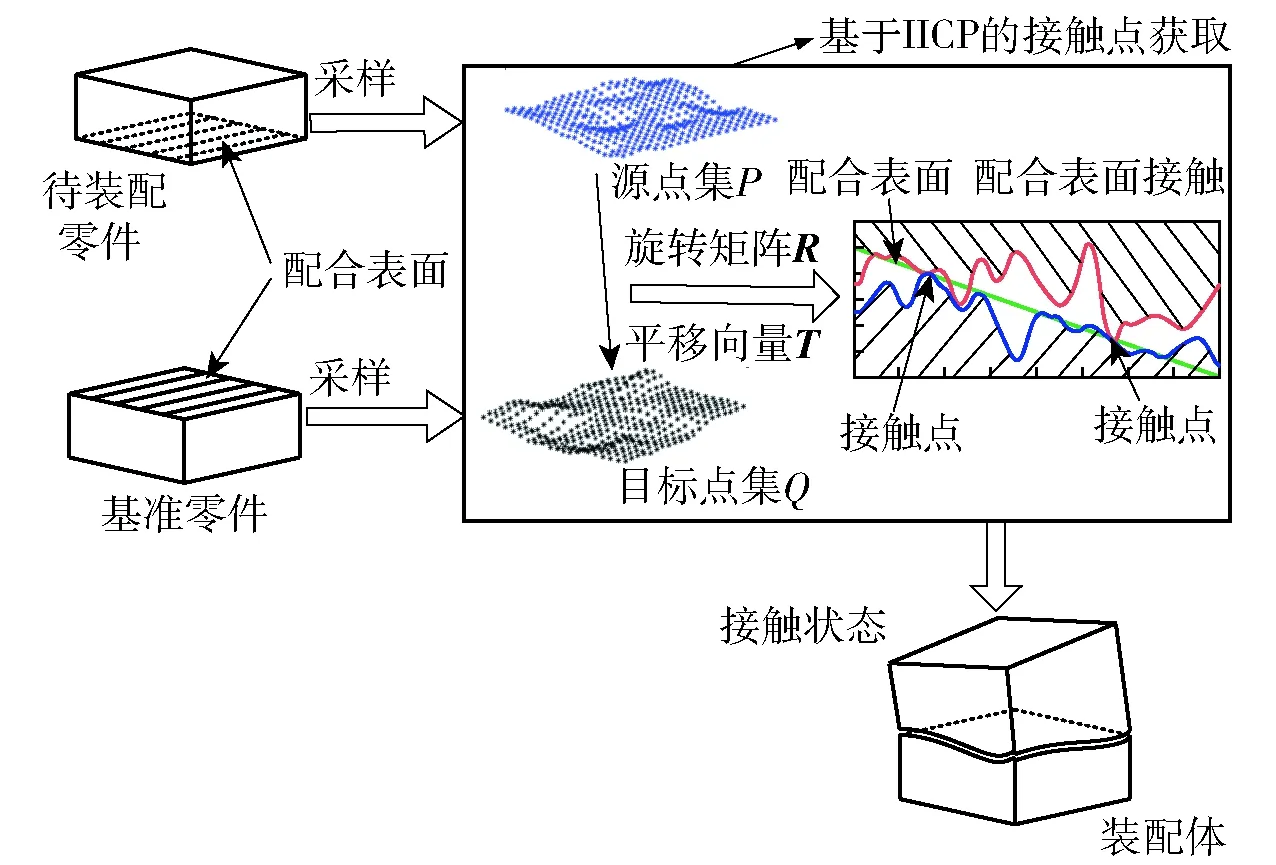
图8 基于数据配准的零件装配过程Fig.8 Part assembly process based on data registration

假设在基准零件配合表面测量获得的点云数据集合为源点集P={p1,p2,…,pi,…,pn}，pi为源点集中的测量点，在基准零件配合表面测量获得的点云数据集合为目标点集Q={q1,q2,…,qi,…,qn}，对源点云中每个点在目标点云中查找欧式距离最近点来确定两个点云的对应关系，然后依据对应关系求解(5)式中的目标函数值最小的刚体变换，并将该变换作用于源点云，迭代地执行这一过程，直至满足设定收敛准则的要求。

(5)

T3×1=[tx,ty,tz] ,

(6)

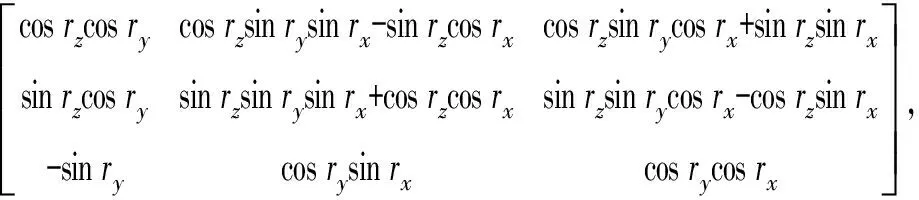
(7)

式中：tx、ty、tz分别表示沿3个坐标轴x、y、z方向的平移量；rx、ry、rz分别为绕坐标轴x、y、z的旋转角度。

当目标函数在条件约束下达到最小值时得到的定位变换称为最佳匹配变换(R*,T*)。因此，基于目标函数与相关约束条件结合零件装配过程建立基于数据配准的迭代过程，具体的算法流程如图9所示。

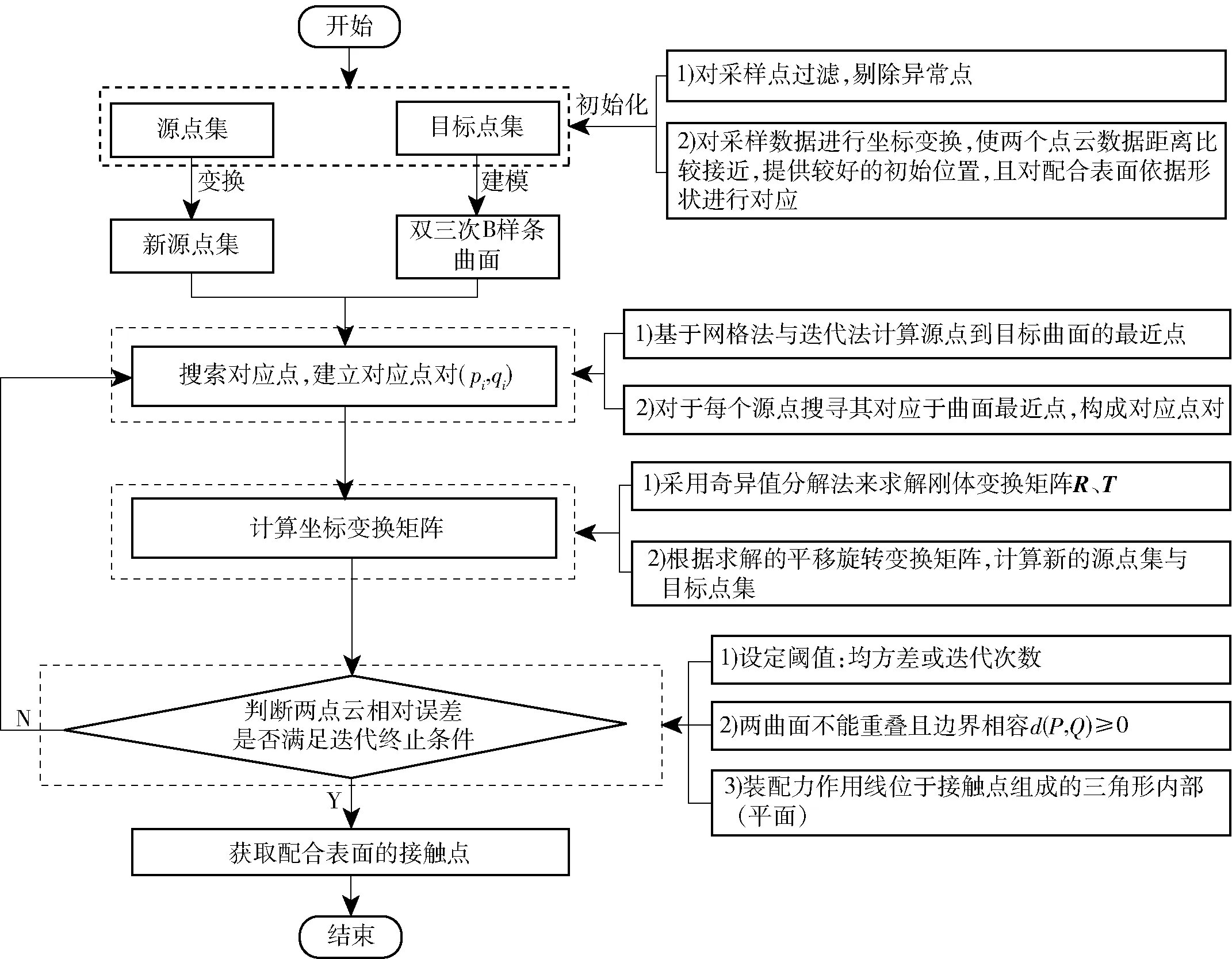
图9 基于点云数据配准的迭代算法流程Fig.9 Flow chart of iterative algorithm based on data registration

在基于点云数据配准的迭代过程中，有3点需要特别关注：

1)对应点的搜索。在整个算法计算过程中，确定两个表面的对应关系是整个算法的关键，对应关系的准确与否，将直接影响算法的精度，同时，可能增加算法的迭代次数。搜索对应点即为建立最近点对应关系，对于源点集之中的每一个点pi在目标曲面上获取源点的对应点qi，对应点即为目标曲面上距离源测量点最近的点。双三次B样条曲面是一种参数曲面，点到参数曲面的最近点位置即点到曲面的投影。假定点pi为源点集中的一点，点qi为曲面上对应与点pi的最近点，那么有方程(pi-qi)×Sn=0成立，其中Sn为曲面在qi处的法向量，通过求解该方程获得最近点，如图10所示。求解点到参数曲面的方法有很多，本文引用文献[14]中牛顿迭代和几何分割的方法求解。

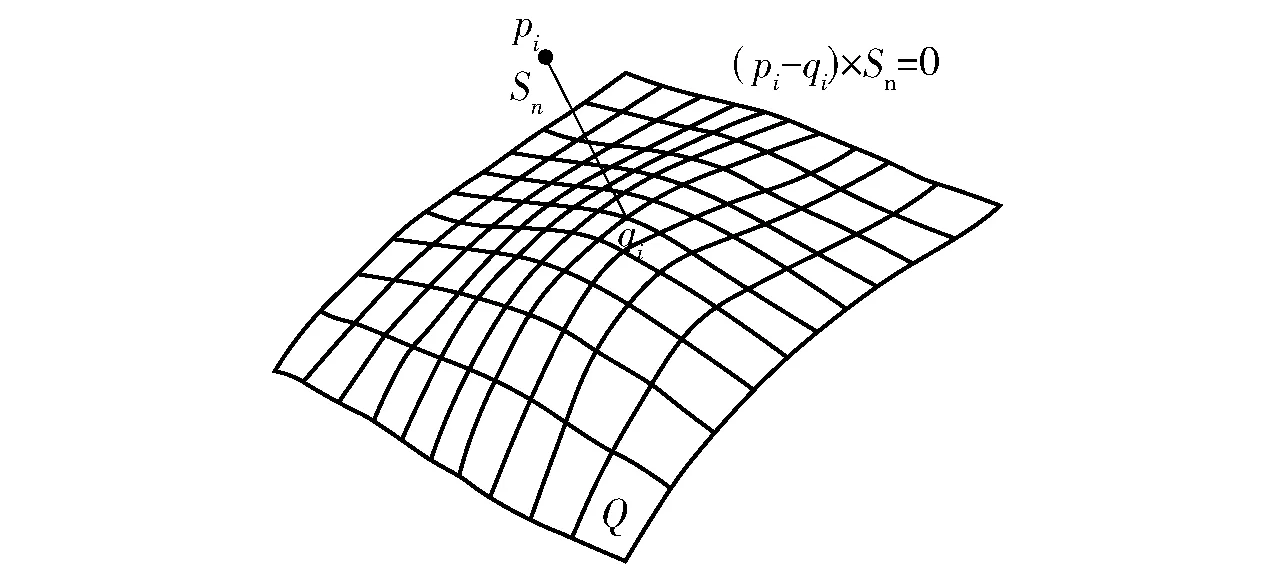
图10 点到参数曲面的距离Fig.10 Distance from point to parametric surface

对于每一迭代不仅获取对应点，还要计算pi与迭代点qi之间的距离记为d(pi,qi)，如果数值为正值则表示源测量点位于目标曲面的上方，反之在下方，如果为0则表示源测量点正好在目标曲面上。

2)刚体变换矩阵的求解。刚体变换的求解是点云配准中重要的环节之一，刚体变换的稳定性在一定程度上影响配准的质量。对于源点集P和目标点集Q，根据对应点对选取原则得到的对应点集合为P={p1,p2,…,pn}，Q={q1,q2,…,qn}，其中(pi,qi)表示一组点对，n表示点的个数，采用奇异值分解法来求解刚体变换矩阵的过程[15]为：

①计算点集P和Q的质心，分别为

(8)

②将点集P和Q中所有点都转换到以各自质心为原点的坐标系下，得到新的点集P′和Q′，其中：

p′i=pi-μp,q′i=qi-μq.

(9)

③利用新的点集P′和Q′，构造一个的3×3矩阵作为基础矩阵M(协方差矩阵)：

(10)

④对M进行奇异值分解，

M=UΛVT，

(11)

式中：Λ为对角阵；U为奇异值分解的酉矩阵；V为分解矩阵。

⑤令

(12)

如果rank(Z)≥2，则旋转矩阵R表示为

R=VZUT.

(13)

⑥求解平移向量T：

T=μq-Rμp.

(14)

3)约束条件。在迭代过程中存在两种情况：一种是在迭代过程中不管如何进行矩阵变换，匹配精度都围绕某一数值小范围的上下波动，此时可结束迭代；另一情况时迭代一直存在，迭代精度一直大范围的变化，此时采用两种方法保证，一种设定迭代终止次数，另外一种是设定两次迭代之后的相对误差，即以目标函数来衡量点云的配准效果，反映了经刚体变换后两个点云之间的差异程度。迭代终止必须满足约束条件：

①阈值的设定：利用目标函数(5)式来评价对应点集的匹配程度，当转换后点对的ICP均方根小于设定阈值则表示达到预期效果。

②两曲面不能重叠且边界相容，即要求被装配曲面与装配曲面之间的距离大于等于0，即d(P,Q)≥0.

③根据配准方法可以获得不止一组可能的接触点，因此，不同类型的表面接触需要根据实际装配情况设定特殊的约束条件。对于平面，为了确定实际的接触点，还需要设置：装配零件的质心相对于零件表面的垂线必须位于3对接触点构成的三角形区域内，如图11所示，p1、p2、p3为接触点，pb是被装配零件的质心。

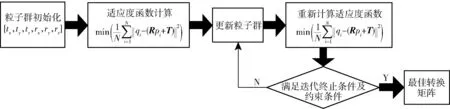
图12 粒子群算法流程Fig.12 Flow chart of particle swarm algorithm

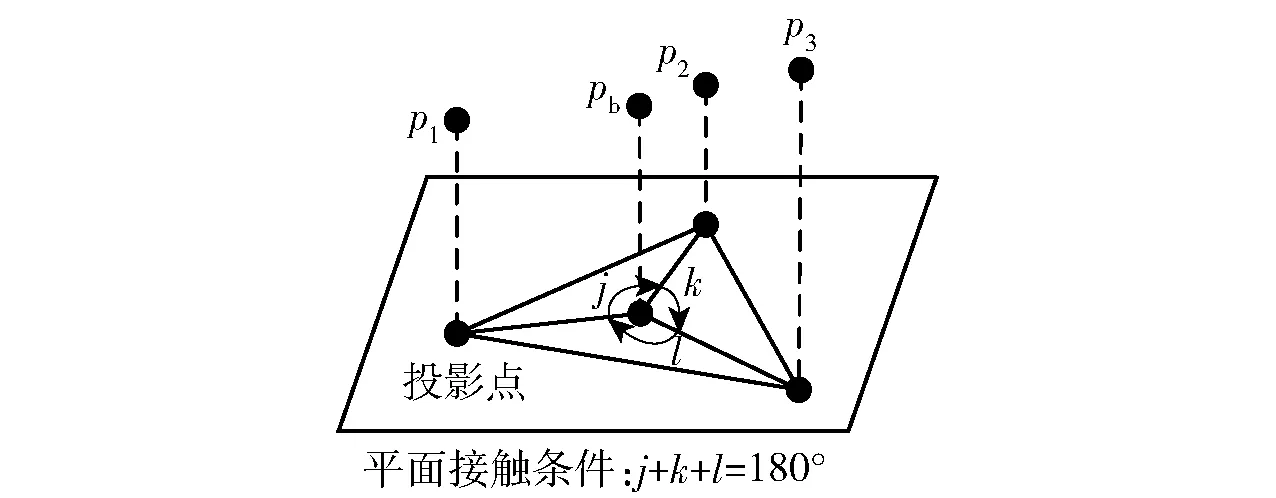
图11 平面接触条件Fig.11 Contact condition

本文采用粒子群算法求解基于点云数据配准的迭代过程，将待求解作为一个粒子，其参数[tx,ty,tz,rx,ry,rz]为粒子的维度[16]。粒子群算法流程如图12所示。

3 基于接触点的配合误差计算

3.1 配合误差表示

两个零件进行装配时，由于两配合表面存在形状误差将引起被装配零件相对于基准零件进行微小变动，从而造成被装配零件实际装配位置与方向相对于理想装配位置与方向的变动量，即引起的被装配零件的位置误差与方向误差，这就是配合误差[17]。

根据两个零件接触点的位置，确定当基准零件位置固定后，如何调整被装配零件的位置和角度以达到两个零件接触点刚好接触的状态，进而完成两个零件的装配。因此首先需要研究零件配合表面特征误差的表示。小位移旋量(SDT)是表示带有6个运动分量的刚体产生微小位移所构成的矢量，SDT方法采用6个变动分量构成的矢量来描述微小位移，即uF=[u,v,ω,α,β,δ]，其中α、β、δ表示绕x、y、z轴旋转的微小变动量，u、v、ω表示绕x、y、z轴平移的微小变动量。本文采用SDT方法描述零件特征误差变动，对于平面配合，由于只关注零件沿z轴方向的误差，因此平面特征误差小位移旋量表示为uF=[0,0,ω,α,β,0]。

如图13所示，对于平面配合，图13(a)中展示了装配前两个零件的位姿状态，基准零件P1的表面特征误差表示为接触点构成的替代表面与理想表面之间的相对误差，即uF1=[0,0,ω1,α1,β1,0]；被装配零件P2的表面特征误差表示为接触点构成的替代表面与理想表面之间的相对误差，即uF2=[0,0,ω2,α2,β2,0]。从而装配体的配合误差即为被装配零件的实际位置相对于理想位置的误差，即

uM=uF1-uF2.

(15)

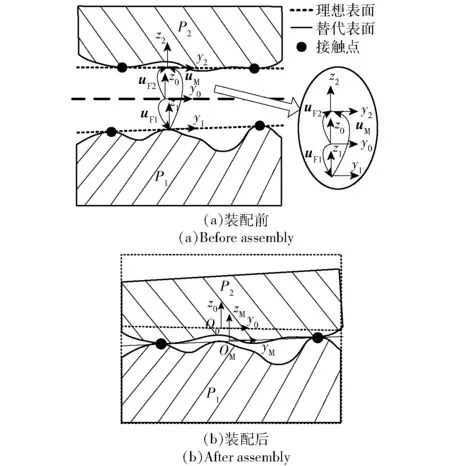
图13 考虑几何形状误差的零件装配Fig.13 Part assembly considering form error distribution

3.2 配合误差计算

根据2.2节得到的两个配合表面上的接触点，可分别确定两个替代要素。当确定了接触的位置后，就可以确定被装配零件的空间位姿，从而确定装配体的装配精度。

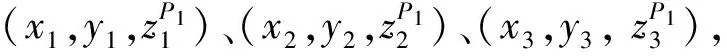
P1:z=A1x+B1y+C1,
P2:z=A2x+B2y+C2,

(16)

式中：A1、B1、C1与A2、B2、C2分别为两平面方程的系数。则零件P1配合平面法向量与x轴和y轴的夹角分别为

cosα1=(n1ex)/(|n1||ex|),
cosβ1=(n1ey)/(|n1||ey|),

(17)

式中：n1为零件P1配合平面法向量；ex、ey分别为x轴和y轴的单位向量。

同理零件P2配合平面法向量与x轴和y轴的夹角分别为

cosα2=(n2ex)/(|n2||ex|),
cosβ2=(n2ey)/(|n2||ey|),

(18)

式中：n2为零件P2配合平面法向量。

若(xc1,yc1)为零件P1配合平面的中心点，则特征误差的z轴方向平移为

ω1=A1xc1+B1yc1+C1.

(19)

同理若(xc2,yc2)为零件P2配合平面的中心点，则特征误差的z轴方向平移为

ω2=A2xc2+B2yc2+C2.

(20)

从而得到零件的配合误差为

uM=uF1-uF2=[0,0,ω1-ω2,α1-α2,β1-β2,0]T.

(21)

4 实例验证

4.1 实验验证

为了验证形状误差及其分布对装配精度的影响，获得两个零件配合时接触状态下产生的配合误差，结合某陀螺仪加工工艺特点开展了本次实验，通过设计、加工、测量相关的零件与装配体，将测量数据与计算结果比较，验证了所提方法的有效性。

如图14所示为零件的装配实例，零件P1和零件P2均为回转体，两者之间为圆形平面与圆形平面接触。零件1是一个上表面具有高精度的基板，作用是为了保证与零件1接触时产生比较小的误差，从而在进行接触状态分析时可以忽略不计，零件2是定位销，起定位作用。在仅考虑零件P1和零件P2处2个配合表面存在的形状误差下，分析配合表面的接触状态，分别计算不考虑形状误差分布与考虑形状误差下的配合误差，验证形状误差及其分布对精密装配的影响。

依据零件的精度要求分别加工各零件，并采用瑞典海克斯康公司产MISTRAL 07.10.07型三坐标测量机测量零件P1的上表面(见图15)、零件P2的下表面以及装配后零件P2的上表面。如图16所示，在零件P1的表面等间隔测量同心圆，每个圆均匀采样60个点，得到各点坐标值，之后同样对零件P2的表面等间隔测量同心圆，每个圆均匀采样60个点。在测量完各零件之后把零件P1、零件P2、零件1、零件2进行装配，然后测量零件P2的表面得到各点坐标值。依据最小区域法评定平面度误差，如表1所示。

采用数据配准的方法进行接触状态分析，获取其最佳的接触状态，刚体变换矩阵如表2所示。经变换后获得3个接触点，如图17和图18所示。

1)接触点确定方法的有效性。当固定基准零件时，调整被装配零件的位姿(刚体变换矩阵)刚好到达接触状态，则即可说明基于数据配准接触点搜索方法的准确性。

图14 零件P1、零件P2以及其装配体的示意图Fig.14 Schematic diagram of Part P1, Part P2 and assembly

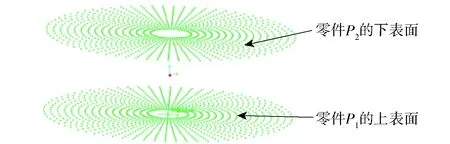
图16 零件P1、零件P2测量点的分布Fig.16 Distribution of measurement points of Part P1 and P2

表2 数据配准变换矩阵

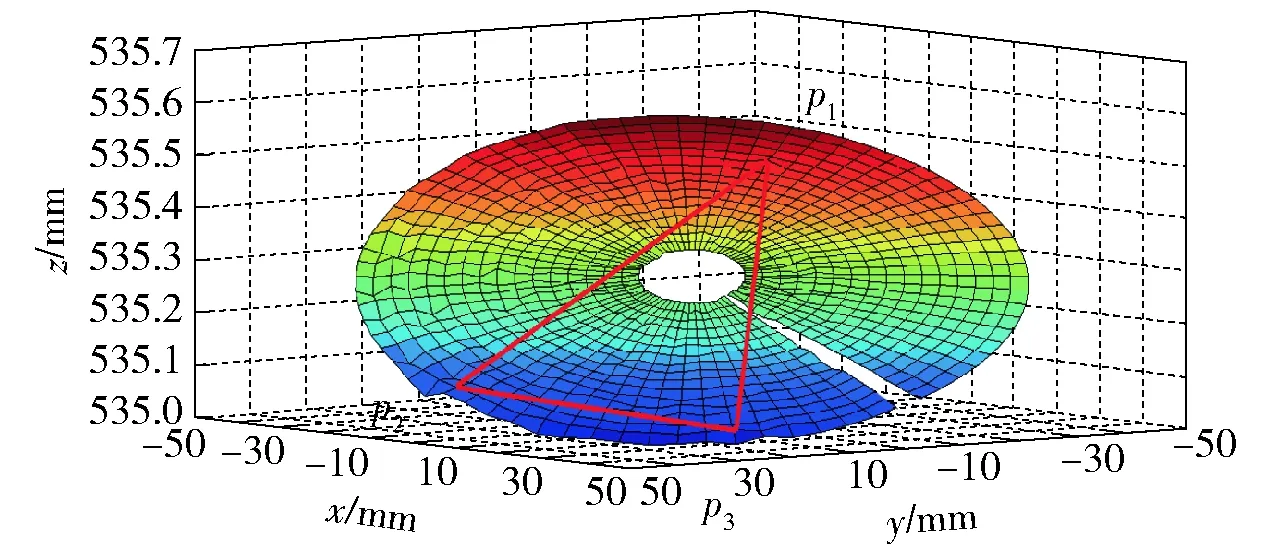
图17 零件P1配合表面接触点p1、p2、p3Fig.17 Contact points p1, p2 and p3 of Part P1

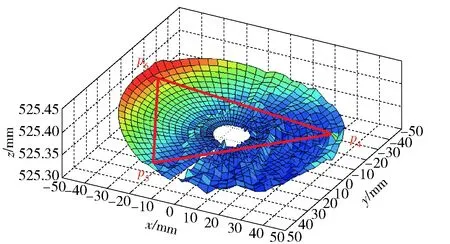
图18 零件P2配合表面接触点p4、p5、p6Fig.18 Contact points p4、p5 and p6 of Part P2

采用数据配准方法获得了零件配合的接触点和刚体变换矩阵。按被装配零件的平移量和旋转矩阵进行位姿变换后，基准零件与被装配零件对应点的距离为1.23×10-11mm、0 mm、2.54×10-12mm，可以说明数据配准方法的有效性和准确性。

2)两种情况下配合误差的比较。在考虑形状误差分布的情况下，计算零件配合表面的配合误差为(其替代接触面(接触点构成的平面)与其名义表面相对误差)：

uM1=[0,0,0.006 8,0.028 6,-0.004 2,0]T.

(22)

同样，在不考虑形状误差分布的情况下，计算零件装配后的配合误差(定义为其最小二乘替代平面与其名义平面的相对误差)为

uM2=[0,0,0.007 2,-0.009 1,-0.012 9,0]T.

(23)

通过对两种结果比较可知，考虑形状误差分布下计算的配合误差明显区别于不考虑形状误差分布获得的配合误差：

①在z方向上的平移，不考虑形状误差分布下零件平移量大于考虑形状误差分布的情况；

②在x方向上的旋转，不考虑形状误差分布下零件向负方向旋转，并且旋转角度小于考虑形状误差分布情况；

③在y方向上的旋转，两种情况都向负方向平移，但不考虑形状误差分布下零件的旋转角度大于考虑形状误差分布情况。

4.2 仿真验证

为了进一步说明形状误差分布对装配精度影响，在实际零件配合验证的基础上进行仿真，从统计意义上验证形状误差对装配精度影响。采用装配成功率指标衡量产品的成品率，装配成功率是指一批零件装配时满足精度要求的装配体数量占装配体总量的比例。

如图14所示两个零件的装配，零件P1、零件P2的设计公差分别如图14(a)和图14(b)所示。为了满足结构的精度要求，假设装配体的平行度公差为0.03 mm，即以零件P1的下表面为基准，约束零件P2上表面的平行度为0.03 mm，如图19所示。利用小位移旋量参数表示零件P2上表面的特征误差[0,0,ω2,α2,β2,0]，并采用文献[18]中的方式建立公差域模型，即一个封闭的圆锥体区域，以此衡量平行度公差的精度要求。圆锥体区域的中心表示误差小，区域边界表示误差越大，超出区域表示不符合精度要求。当装配体误差的实际小位移旋量值超出公差域时，认为装配体无法满足精度需求，即产品不合格；否则，认为产品合格。

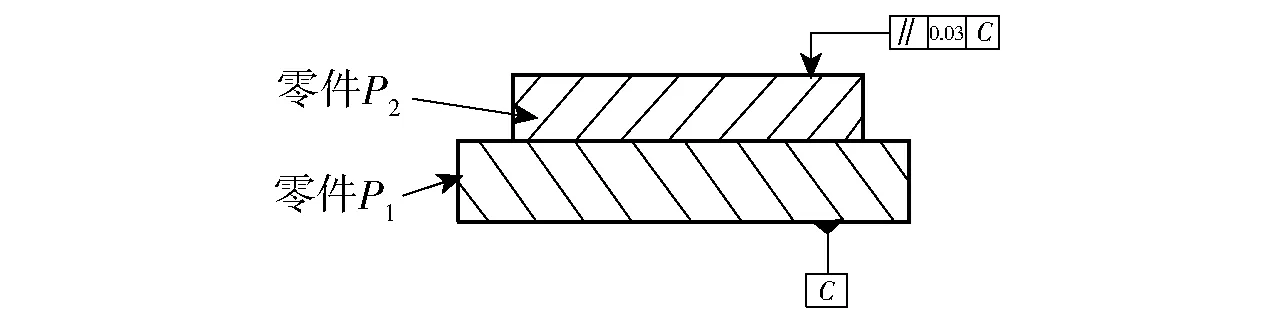
图19 装配体的精度要求Fig.19 Precision requirement of assembly

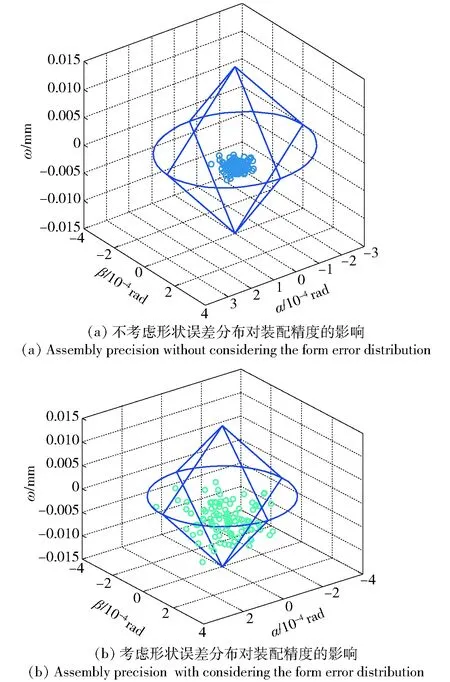
图20 形状误差对装配精度分布的影响Fig.20 Influence of form error on assembly precision

通过仿真在零件P1的上表面(5圈，每圈30个点)、零件P2的下表面(5圈，每圈30个点)上生成100组测量点云数据，零件P1上表面的点云数据服从正态分布μ=-0.002，σ2=0.002 5，零件P2下表面的点云数据服从正态分布μ=0.002，σ2=0.002 5. 图20显示了不考虑和考虑形状误差分布对装配精度的影响：由图20(a)可知，在不考虑形状误差分布的情况下，该装配体满足精度要求，装配成功率100%，并且误差的分布比较集中；由图20(b)可知，在考虑形状误差分布的情况下，该装配体有92%满足精度要求(装配成功率92%)，并且误差的分布比较分散。因此，形状误差的分布对精密装配的装配精度具有重要影响，在研究装配时不可忽视。

5 结论

本文提出了基于数据配准的配合表面最佳接触状态的确定方法，确定了形状误差的分布对装配精度具有重要影响，实现了装配精度的初预测，结论如下：

1) 分析了零件表面几何形状误差分布特性，提出了一种考虑形状误差分布的基于数据配准的配合表面接触状态确定方法，通过确定零件装配时的接触点位置和零件的接触状态，实现精密高刚度零件装配精度的预测。

2) 提出了基于接触状态的配合误差计算方法，可用于预测精密高刚度零件装配精度，指导装配工艺优化，从而提高装配精度。

3) 采用数值仿真方法对比考虑和不考虑形状误差分布对装配精度影响两种情况下的装配成功率，从统计意义上说明形状误差对精密刚度零件装配精度的影响不可忽视。

采用本文所提方法需要在迭代过程中计算点到曲面的距离，这样将降低迭代效率；本文以平面接触作为例子进行说明，对于其他表面如圆柱面的配合的特殊性，接触的约束条件存在不确定性，后续还需要对以上问题进一步研究。

)

[1] Liu F, Xu G H, Liang L, et al. Minimum circumscribed circle and maximum inscribed circle of roundness deviation evaluation with intersecting chord method[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(12): 2787-2796.

[2] 周东栋, 樊军. 基于改进粒子群算法的平行度误差评定[J]. 组合机床与自动化加工技术, 2016(2): 108-111.

ZHOU Dong-dong, FAN Jun. Parallelism error evaluation based on an improved particle swarm optimization[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(2): 108-111.(in Chinese)

[3] Endriasa D H, Hsiyung F, Ji M, et al. A combinatorial optimization approach for evaluating minimum-zone spatial straightness errors[J]. Measurement, 2012, 45(5): 1170-1179.

[4] 郭崇颖, 刘检华. 基于几何特征变动向量的几何误差评定方法研究[J].计算机集成制造系统, 2015, 21(10): 2604-2612.

GUO Chong-ying, LIU Jian-hua. Evaluation of geometry error based on deviation vector of geometry feature[J]. Computer Integrated Manufacturing Systems, 2015, 21(10):2604-2612. (in Chinese)

[5] Grandjean J, Ledoux Y, Samper S. On the role of form defects in assemblies subject to local deformations and mechanical loads[J]. International Journal of Advanced Manufacturing Technology, 2013, 65:1769-1778.

[6] Jin X, Zuo F, Zhang T, et al. An entropy-based method to evaluate plane form error for precision assembly[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2013, 227(5): 726-734.

[7] 吕程, 刘子健, 艾彦迪, 等. 多公差耦合装配结合面误差建模与公差优化设计[J]. 机械工程学报, 2015, 51(18):108-118.

LYU Cheng, LIU Zi-jian, AI Yan-di, et al. Assembly joint surface error modeling and tolerance optimization in the case of coupled tolerance[J]. Journal of Mechanical Engineering, 2015, 51(18): 108-118. (in Chinese)

[8] 唐水龙, 余剑锋, 李原, 等. 基于虚拟配合面的带平面度零件装配容差分析[J]. 计算机集成制造系统, 2011, 17(4):711-715.

TANG Shui-long, YU Jian-feng, LI Yuan, et al. Assembly tolerance analysis for parts with flatness based on virtual mating plane[J]. Computer Integrated Manufacturing Systems, 2011, 17(4): 711-715. (in Chinese)

[9] 左富昌, 张之敬, 金鑫, 等. 考虑平面形状误差的配合表面接触状态研究[J]. 兵工自动化, 2012, 31(9):32-37.

ZUO Fu-chang, ZHANG Zhi-jing, JIN Xin, et al. Research on contact state of mating surfaces taking into account plane form error[J]. Ordnance Industry Automation, 2012, 31(9):32-37. (in Chinese)

[10] Henke R, Summerhays K D, Baldwin J M, et.al. Methods for evaluation of systematic geometric deviations in machined parts and their relationships to process variables[J]. Precision Engineering, 1999, 23(4): 273-292.

[11] 张婷玉. 精密机械系统装配精度预测与控制方法研究[D]. 北京:北京理工大学, 2016.

ZHANG Ting-yu. Assembly accuracy prediction and control for precision mechanical system[D]. Beijing: Beijing Institute of Technology, 2016.(in Chinese)

[12] 彭和平, 刘晓军. 考虑形位公差的二维装配公差分析[J]. 机械传动, 2008, 32(3):75-77.

PENG He-ping, LIU Xiao-jun. Tolerance analysis of 2D assembly considering geometrical tolerance[J]. Journal of Mechanical Transmisson, 2008, 32(3): 75-77. (in Chinese)

[13] 孙家泽, 陈皓, 耿国华. 三维文物点云模型配准优化算法[J]. 计算机辅助设计与图形学学报, 2016, 28(7):1068-1074.

SUN Jia-ze, CHEN Hao, GENG Guo-hua. Registration optimization algorithm for 3d cultural relics point clouds model[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(7): 1068-1074. (in Chinese)

[14] Selimovic I. Improved algorithms for the projection of points on NURBS curves and surfaces[J]. Computer Aided Geometric Design, 2006, 23(5): 439-445.

[15] Ko K H, Maekawa T, Patrikalakis N M. Algorithms for optimal partial matching of free-form objects with scaling effects[J]. Graphical Models, 2005, 67(2): 120-148.

[16] Shi Y. Particle swarm optimization: developments, application and resources[C]∥Proceedings of the 2011 Congress on Evolutionary Computation. Seoul, South Korea:IEEE, 2001: 81-86.

[17] 左富昌. 精密机械系统误差传递机理与装配精度控制方法[D]. 北京:北京理工大学, 2012.

ZUO Fu-chang. Variation propagation mechanism and assembly accuracy control methodology for precision mechanical system[D]. Beijing: Beijing Institute of Technology, 2012.(in Chinese)

[18] Davidson J K, Mujezinovic A, Shah J J. A new mathematical model for geometric tolerances as applied to round faces[J]. Journal of Mechanical Design, 2003, 124(4): 609-622.