基于B样条曲线的4WIS电动汽车转向模式动态切换与控制方法

来 鑫，谢万军，姜 淳，孙 涛

（上海理工大学 机械工程学院，上海 200093）

4WIS电动汽车的每个车轮都可以独立控制，能够完成前轮转向、后轮转向、四轮转向、原地转向等多种转向模式[1]，可控自由度冗余度大（冗余度为2n－3，n为车轮个数，n≥3），车辆的机动性和可操纵性强，可以满足如今日益苛刻的对汽车灵活性、自动化及智能化的要求。4WIS电动汽车可应用于工业、农业、军事、宇宙探索等多个领域，成为汽车领域的研究热点。美国、西班牙、日本等国家的汽车公司及科研机构对4WIS电动汽车进行了研究，实现了该车辆的多种转向模式自由切换，也提出了多种动力学控制方法与策略[2-6]。哈尔滨工业大学对可重构底盘进行了设计，定义了4WIS电动汽车的7种运动模式，山东大学、吉林大学、同济大学等高校也对该车辆的结构、运动学及动力学等方面进行了大量的研究[7-11]。但是，国内外的这些研究基本都集中在对车辆的运动学与动力学控制策略上，转向模式的切换需在停车后完成。然而，随着转向要求的提高与汽车所处环境的日益复杂，停车切换严重影响了车辆的行驶安全性、机动性及智能性。因此，在充分利用4WIS电动汽车的冗余自由度的基础上，探索在不停车情况下4WIS电动汽车的转向模式是十分必要的。

本文在研究4WIS电动汽车动力学模型的基础上，提出一种基于B样条曲线的车轮轨迹规划方法，以前轮转向切换到后轮转向为例，对各独立车轮的运动轨迹进行运动规划，实现该车辆转向模式的不停车动态切换。在切换控制方法上通过求解瞬时转向中心，提出一种复合控制策略，通过仿真研究验证运动轨迹规划控制策略的有效性。

1 4WIS电动汽车的动力学建模

为了简化4WIS电动汽车的动力学建模过程，做如下假设：

（1）忽略悬架作用，车辆只做平行于地面的平面运动，即车辆沿z轴位移，绕y轴俯仰角和绕x轴侧倾角均为0。

（2）车辆侧向加速度限定在约3.92 m/s2以下，轮胎侧偏特性处于线性范围，不考虑地面切向力对轮胎侧偏特性的影响。

在上述假设下将4WIS电动汽车简化为一个线性二自由度模型，如图1所示。

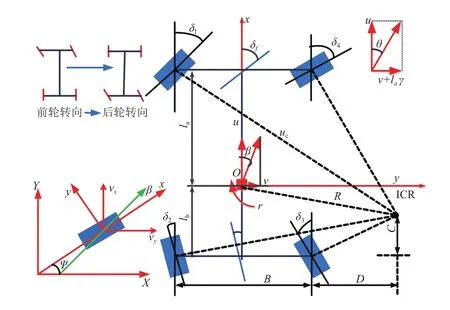
图1 车辆二自由度模型示意图

图1中：定义俯视时车轮顺时针转动为正；u为车辆纵向速度，m/s；v为车辆侧向速度，m/s；la为车辆质心到前轴的距离，m；lb为质心到后轴的距离，m；γ为车辆横摆角速度，rad/s；uc为质心合速度，m/s；ICR为瞬时转向中心，m；β为质心侧偏角，rad；δ1、δ2、δ3、δ4为左前轮、左后轮、右后轮、右前轮的转向角，rad；Cαf、Cαr为前后轮胎侧偏刚度，N/rad；X、Y为固定坐标系下车辆质心纵向和侧向位移，m；Vx、Vy为固定坐标系下车辆质心的纵向和侧向速度，m/s；Ψ为固定坐标系下车辆的横摆角，rad/s。

对图1所示的车辆模型进行受力分析，4WIS电动汽车二自由度微分方程为：

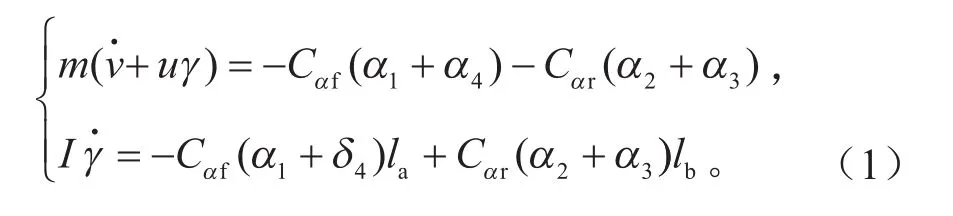
式中：α1、α2、α3、α4分别为 4个车轮的侧偏角，rad。由于四轮转向角均很小，同时u＞＞βγ/2，忽略βγ/2，整理得各车轮轮胎侧偏角如下：

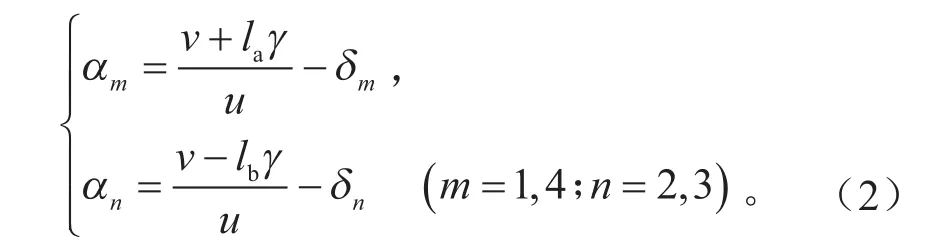
根据阿克曼几何原理可得4个独立车轮转向角之间的关系为：

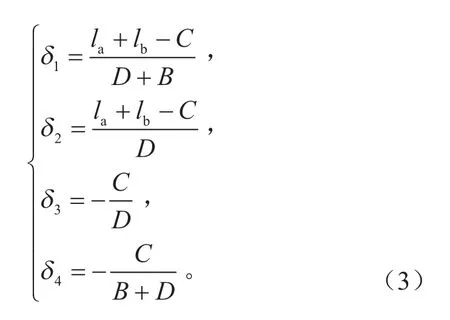
车辆的质心侧偏角为：

将式（2）～（4）代入式（1）中，整理得：

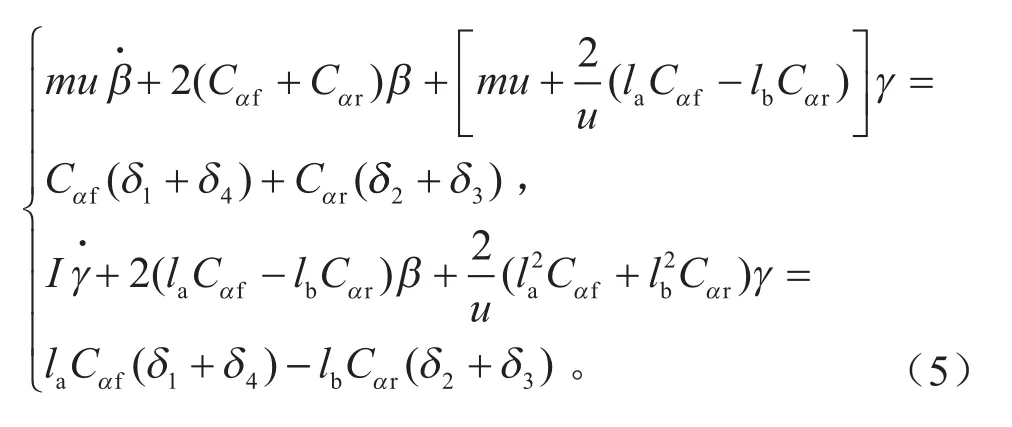
对于4WIS电动汽车，采用的控制策略为：（a）车辆稳定时质心偏转角β = 0；（b）稳态时横摆角速度γ保持恒定。由式（5）可得：

式中：k为前、后轮转向角的比值。假设δ4为主动转向角，将其它车轮转向角转换成与车轮4转向角的关系，如下：

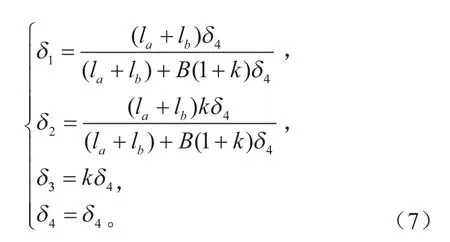
由式（4）可知，为了保持车辆的运动学要求，4个车轮的转向角均与车轮4的转向角相关，定义该角度为参考轮角度，它们之间的关系与车辆的几何尺寸、系数k等密切相关。系数k与车速、车辆的几何尺寸、轮胎的侧偏刚度等相关。

车辆的转向半径R为：

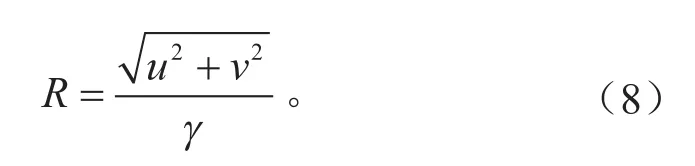
在固定坐标系下，车辆的质心运动轨迹方程为[13]：

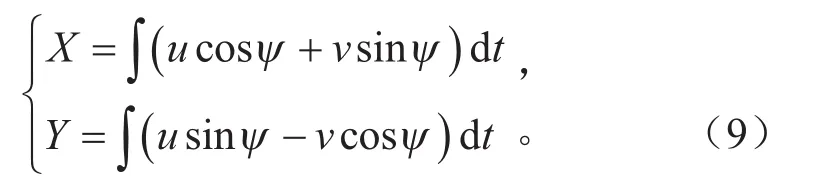
2 基于B样条曲线的车轮运动轨迹规划方法

在研究车辆路径规划时一般采用圆弧+直线或分段函数的方式构造车辆的轨迹，该方式对轨迹的构建简单且易实现，但是车辆的动力学参数可能会产生突变[14]。B样条曲线具有连续性的特点，可以在每一段内无限可微，通过修改几个控制点就可以对局部曲线进行修改。因此，本文采用B样条曲线来规划转向模式切换时车轮的轨迹。B样条曲线表达式如下[15]：

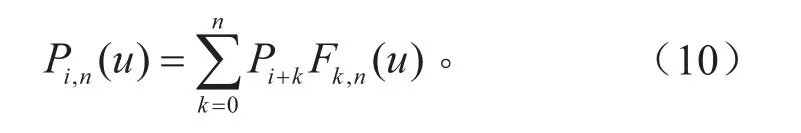
式中：u∈[0，1]；i=1，2，…，m，i为第i段 B样条曲线，m表示曲线由m条样条曲线平滑连接而成；n为样条曲线阶次；Pi+k为第i段B样条曲线的第k个控制点；Fk，n为n次B样条曲线的基函数，其表达式为：

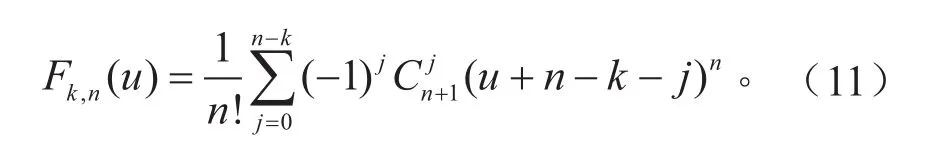
在实际操作中，由曲率公式可知，为了满足转向模式切换过程中曲率的连续性，规划的样条曲线方程最少两次可导。因此，3次4阶B样条曲线满足要求。本文动态切换选用的曲线为4次5阶，根据式（10）与式（11）可得到4次5阶B样条基函数公式为：

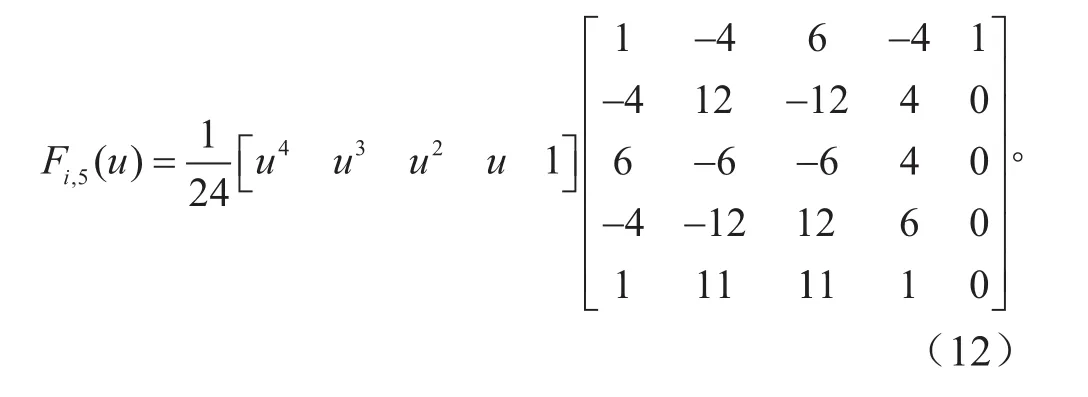
以前轮转向切换到后轮转向为例，借助式（10）～（12）设计一条B样条曲线，选取的9个控制点坐标为（0， 5）、（2， 5）、（3， 5）、（5.3， 5）、（5.5， 2.5）、（5.6， 0）、（5.7， 0）、（8， 0）、（10，0），该曲线0～5 s是输入5°的转向角，5～6 s时发生变化，6～10 s保持不变为0°，生成一条符合前轮转向到后轮转向要求的B样条曲线。以B样条作为模型的输入，建立车辆的动力学及运动学方程，对车辆的运动轨迹及动力学参数进行仿真研究。仿真参数见表1，仿真结果如图2～4所示。

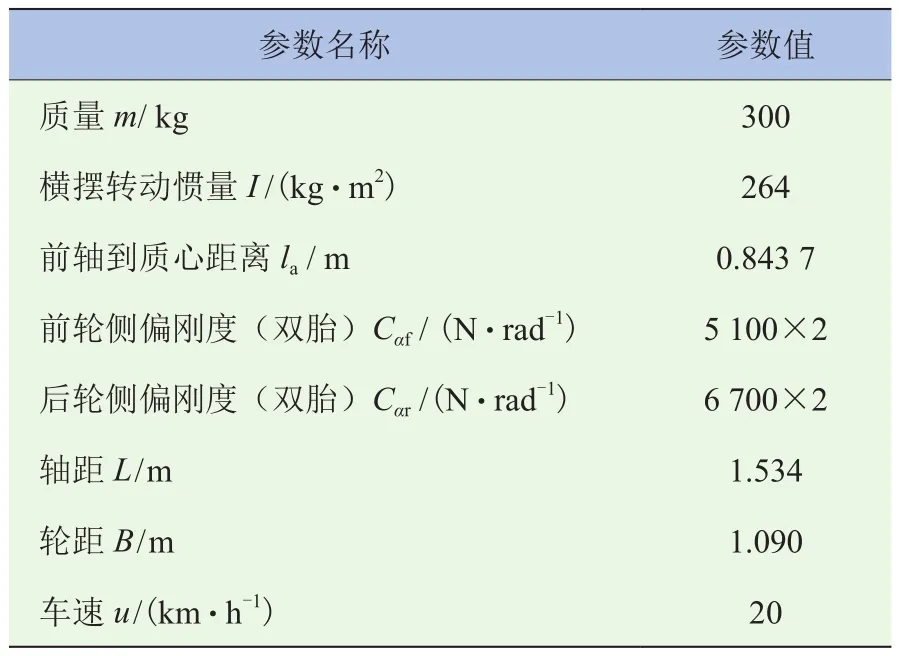
表1 4WIS电动车基本仿真参数

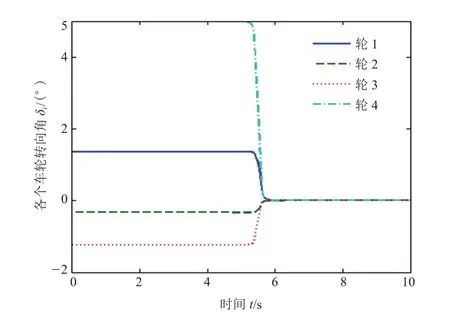
图2 四个车轮转角仿真曲线

图3 质心轨迹曲线

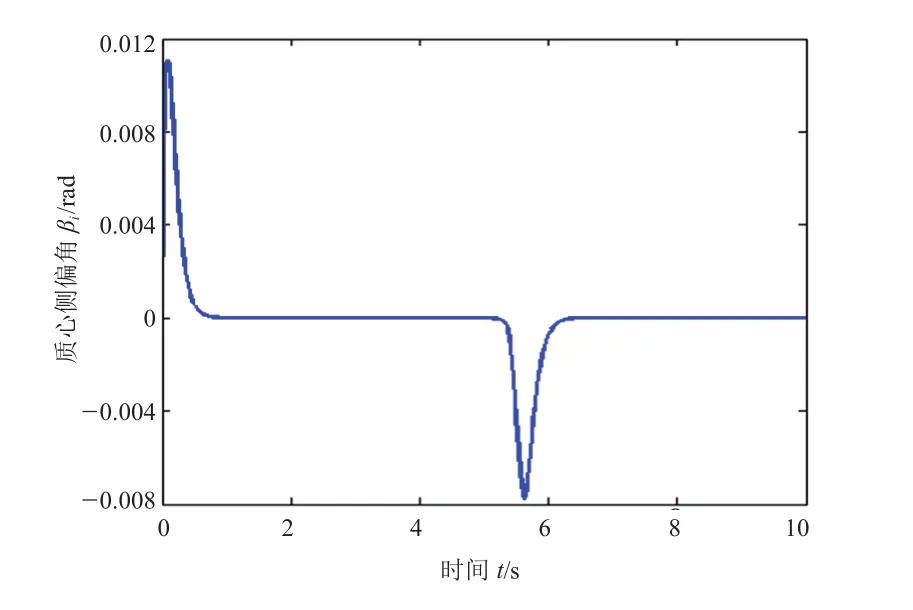
图4 质心侧偏角响应

从仿真结果来看，利用B样条曲线实现了4WIS电动汽车前轮转向与后轮转向的转向模式不停车切换，质心轨迹平滑，质心侧偏角满足要求，验证了所提出的方法的可行性。

3 4WIS转向模式动态切换控制方法

3.1 基于瞬时转向中心的运动学建模

4WIS电动汽车的模式切换控制是通过控制4个独立的转向电机来实现的。由式（7）可知，把车轮4作为基准转向车轮，其它车轮的转向角可通过基准转向角求得，这种控制策略比较简单。但是这种控制策略存在以下问题：跟随车轮转向角是相互独立的，当某个车轮的转向角受到外界干扰时，其它车轮的转向角（包括基准车轮）不能随之进行相应的调整，这时车辆的动力学参数受到影响。因此，必须建立一种能够实时反映4个车轮转向角之间实时关系的控制策略。

车辆在转向模式切换过程中，可以通过各车轮的位置求解瞬时转向中心的坐标来建立各独立车轮之间的虚拟连接。如图1所示，设在车辆坐标系中假设车辆瞬时转向中心ICR坐标为()，车轮i的旋转轴为AXi。当AXi相交于一点时，说明4个车轮满足运动学要求（满足阿克曼几何学原理）；当 不相交时，定义ICR为到各个车轮旋转轴AXi的距离之和最小的点。设ICR到AXi的距离为di，求解车辆瞬时转向中心就是求解到各车轮旋转轴距离之和最小的点，即：

式（13）中，di可以表示为：

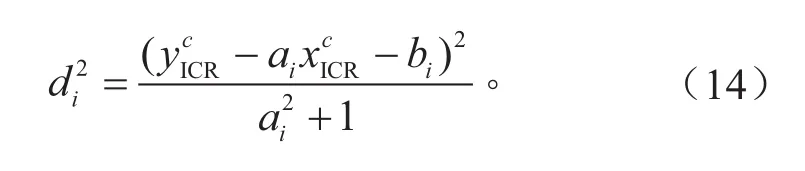
式中：ai= tan(δic+π/2) ；bi= yi-aixi。

由多元函数求取极值条件得：

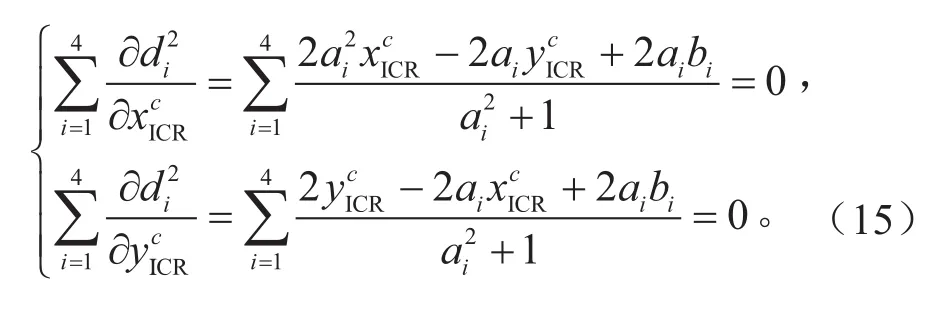
求解式（15）的方程组可以求出瞬时转向中心的坐标值：

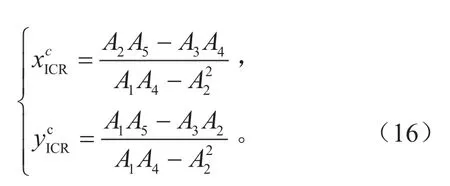
式（16）中：

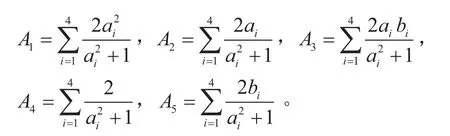
以瞬时转向中心为基础，可以得出各个车轮实时运动学约束角度为：

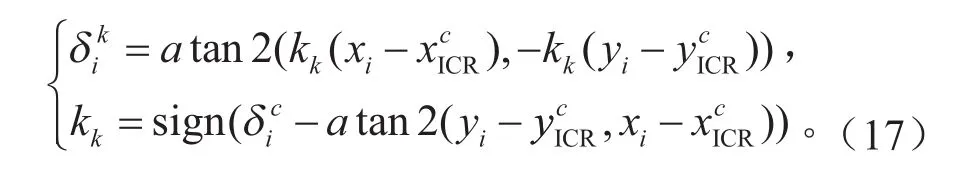
因此，实时运动学误差可以表示为：

由式（18）可知，通过实时转向中心坐标，建立了4个独立车轮转向角之间的虚拟连接。

同时定义动力学误差为：

式中：δTi为目标转向角；δci为当前转向角的瞬时值。

3.2 转向模式动态切换控制动态仿真

动力学约束模型能够保证车辆的动力学要求，基于瞬时转向中心ICR的车辆运动学关系，建立4个车轮之间的虚拟连接，通过实时运动学误差来协调各个车轮的运动，在受到外界干扰时能够及时做出反应。因此，由式（18）和式（19）提出一种“动力学—运动学”复合控制策略，该控制策略设计控制器消除运动学误差及动力学误差。控制算法采用PID控制。

基于以上模型，利用Matlab/Simulink建立4WIS电动汽车的仿真模型，对控制策略进行仿真研究。仿真时设定车辆的质心坐标为（0，0），车辆的初始速度为20 km/h，4个车轮的初始坐标为：(x1, y1)=(-0. 5 45, 0. 8437)，(x2,y2)=(- 0. 5 45, -0. 6903))，(x3,y3)=(0 . 5 45, 0. 8437)，(x4,y4)= ((0 . 5 45, -0. 6903)。

基准车轮4遵循B样条曲线，在仿真时间t=2-3 s时，在车轮1的运动轨迹上加一个0.2 rad的方波，使其转向角发生突变，用以模拟干扰，验证控制策略的有效性，仿真结果如图5～8所示。

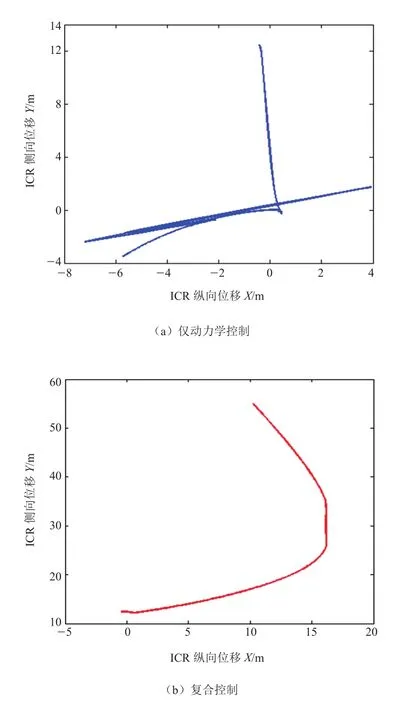
图5 动态切换控制下瞬时转向中心轨迹仿真曲线

图5a为仅有动力学控制的瞬时转向中心ICR仿真曲线，图5b为复合控制下的瞬时转向中心ICR仿真曲线。对比两种曲线可以看出复合控制下ICR的轨迹更加平稳。

图6为质心运动轨迹仿真曲线，可以看出在转向模式切换过程中采用复合控制车辆的转向半径更小。

采用基于ICR运动学复合控制时，从图7b可以看出当车轮1受到干扰转向角发生改变时，其它车轮也会发生改变，从而保证了瞬时转向中心对的稳定性。

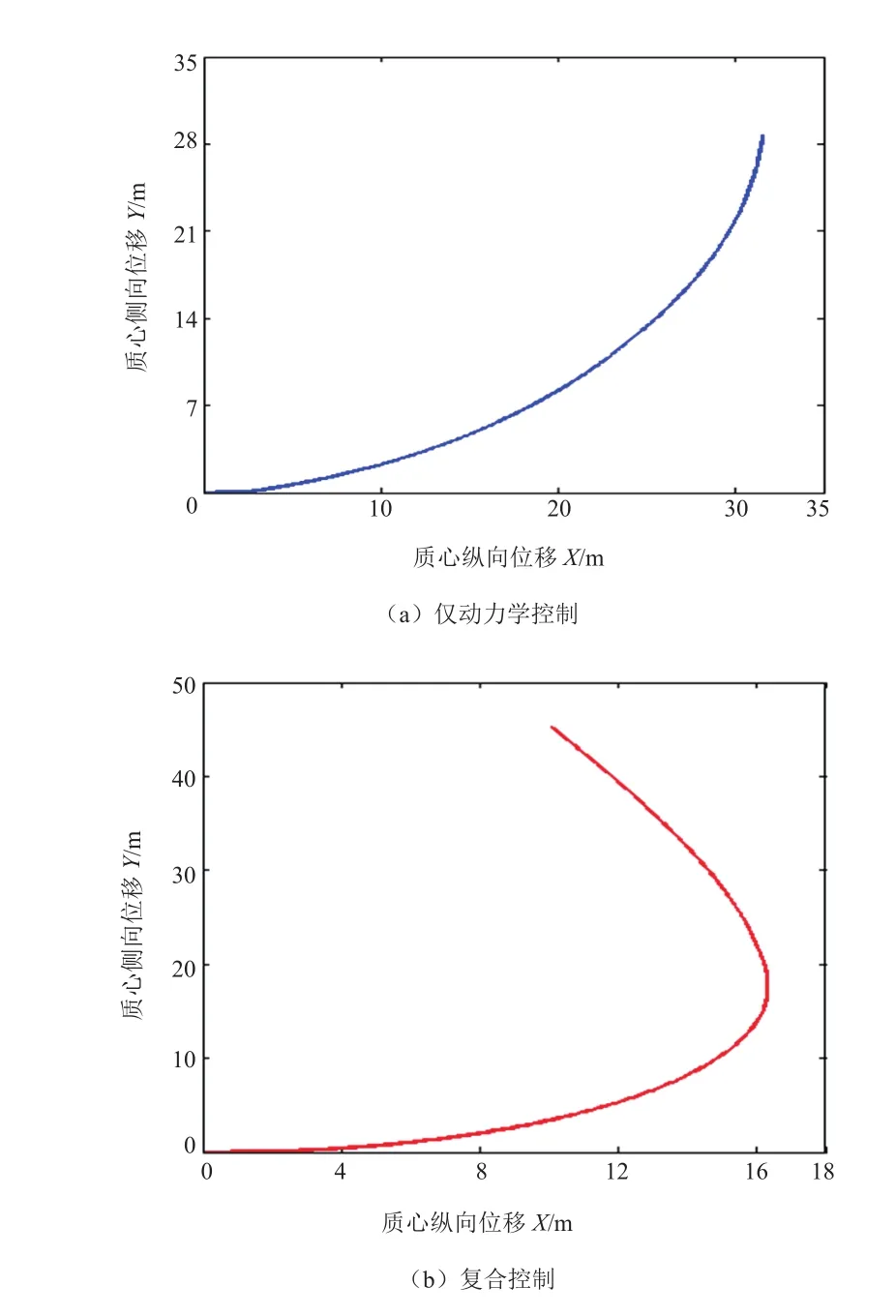
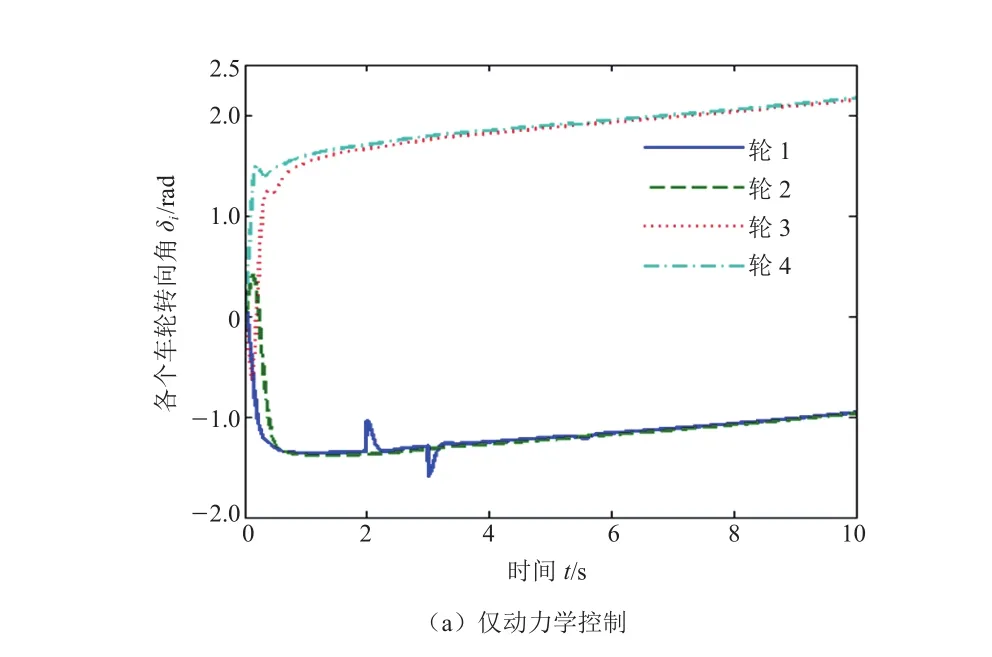
图6 动态切换控制下质心运动轨迹仿真曲线

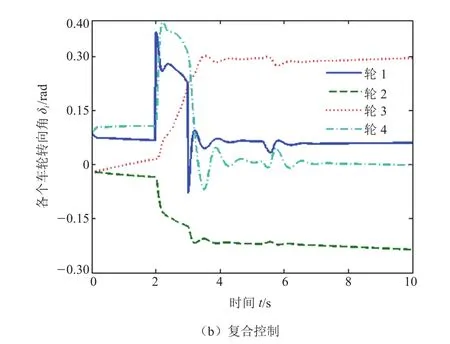
图7 切换控制过程中车轮转向角仿真曲线

图8 加干扰后车轮动力学参数对比

由图8可知，在受到干扰时，车辆的瞬时转向中心、质心运动轨迹和横摆角速度都能很快地稳定下来，验证了复合控制的有效性。

4 试验研究

通过对4WIS电动汽车进行试验研究来验证所提出的控制算法的有效性，采用的试验车辆如图9所示。

图10和图11分别为前轮到四轮转向切换和四轮转向稳态时4个车轮的实时转角试验数据。由此可知，各个车轮转向角之间的关系基本符合式（7），从而验证了所提出的控制策略与方法的有效性。

图9 试验车辆

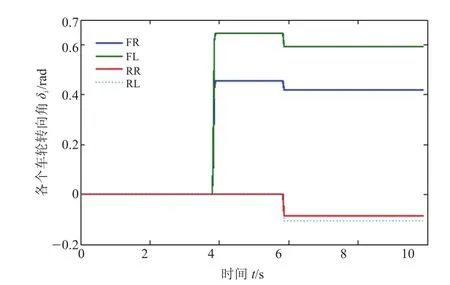
图10 前轮到四轮转向切换四轮转角

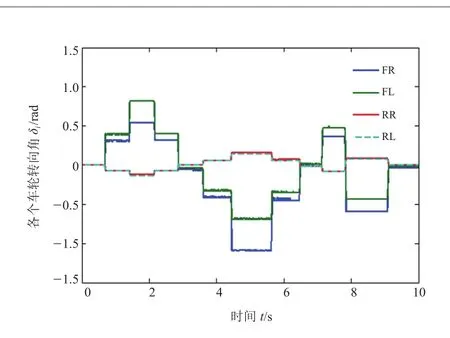
图11 四轮转向稳态时各车轮转向角

5 结论

（1）建立4WIS电动汽车二自由度动力学模型，得出4个独立车轮之间的实时转向角关系，在此基础上建立了4WIS电动汽车的仿真模型。

（2）提出一种基于B样条曲线的车轮轨迹规划方法，实现了前轮转向模式动态切换到后轮转向模式。仿真结果表明，该方法能够实现转向模式的动态切换，切换轨迹平滑，符合运动学及动力学的要求。

（3）在转向模式切换控制方法上，基于瞬时转向中心的实时求解，构建4个独立车轮转向角之间的虚拟连接。提出一种“运动学-动力学”复合控制策略。仿真结果表明，当某个车轮受到干扰时，其余车轮转向角也随之改变，保持了转向模式切换时车辆动力学参数的稳定性，提高了控制系统的鲁棒性。

参考文献（References）：

[1]马雷，贡士娇，李斌，等. 四轮独立转向电动车转向控制方法[J].汽车工程，2015，37(9)：1029-1034，1046.MA Lei，GONG Shijiao，LI Bin，et al. Steering Control Scheme for Electric Vehicles with Four Wheel Independent Steering [J]. Automotive Engineering，2015，37(9)：1029-1034，1046. (in Chinese)

[2]DENG Zhijun，ZHU Rongdong. Research on Stability Simulation for Four Wheel Independent Steering Electric Vehicle [J]. Advanced Materials Research，2012(512-515)：2657-2661.

[3]CHRISTENSEN T B. Modularised Eco-innovation in the Auto Industry [J]. Journal of Cleaner Production，2011，19(2-3)：212-220.

[4]FU Yili，HE Xu，MA Yulin. A Navigation Robot with Recon fi gurable Chassis and Bionic Wheel[C]//Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetic，2004：485-489.

[5]OKSANEN T，LINKOLEHTO R. Control of Four Wheel Steering Using Independent Actuators [J]. IFAC Proceedings Volumes，2013，46(18)：159-163.

[6]LIU Q J，CHEN S Z，ZHANG J W. The Simulation of Four Wheel Steered Car Run in Close-loop Driving Conditions [J]. Applied Mechanics and Materials，2014，543-547：1515-1519.

[7]金立生，高琳琳，谢宪毅，等. 四轮独立转向车辆稳定性的模糊最优控制方法 [J]. 西南交通大学学报，2016，51(6)：1064-1072.Jin Lisheng，Gao Linlin，Xie Xianyi，et al. Fuzzy optimal Control of Four Wheel Independent Steering Vehicles [J]. Journal of South West Jiaotong University，2016，51(6)：1064-1072. (in Chinese)

[8]杨福广，阮久宏，李贻斌，等. 4WID-4WIS车辆横摆运动AFS+ARS+DYC模糊控制 [J]. 农业机械学报，2011，42(10)：6-12.YANG Fuguang，RUAN Jiuhong，LI Yibin，et al.4WID-4WIS Vehicle Yaw Control Based on Fuzzy Logic Control of AFS +ARS +DYC [J]. Transactions of the Chinese Society for Agricultural Machinery，2011，42(10)：6-12.(in Chinese)

[9]宗长富，刘经文，郑宏宇，等. 4WID/4WIS电动车建模和特殊工况仿真 [J]. 汽车工程，2011，33(10)：829-833.ZONG Changfu，LIU Jingwen，ZHENG Hongyu，et al.Modeling and Special Conditions Simulation of Electric Vehicle with 4WID/4WIS [J]. Automotive Engineering，2011，33(10)：829-833. (in Chinese)

[10]来鑫，陈辛波，武晓俊，等. 四轮独立驱动与转向电动车辆运动控制系统及控制策略研究[J].汽车工程学报，2015，5(5)：334-340.LAI Xin，CHEN Xinbo，WU Xiaojun，et al. Study on Motion Control Systems and Algorithms for Four-Wheel Independent Driving and Steering Electric Vehicles [J].Chinese Journal of Automotive Engineering，2015，5 (5)：334-340. (in Chinese)

[11]冯源，余卓平，熊璐. 基于状态反馈的分布式驱动电动汽车操纵性改善控制方法 [J]. 机械工程学报，2013，49(24)：135 - 143.FENG Yuan，YU Zhuoping，XIONG Lu. Handling Improvement for Distributed Drive Electric Vehicle Based on state Variable Feedback Control [J]. Journal of Mechanical Engineering，2013，49(24)：135-143. (in Chinese)

[12]熊璐，陈晨，冯源. 基于Carsim/Simulink联合仿真的分布式驱动电动汽车建模 [J]. 系统仿真学报，2014，26(5)：1143-1148，1155.XIONG Lu，CHEN Chen，FENG Yuan. Modeling of Distributed Drive Electric Vehicle Based on Co-simulation of Carsim/Simulink [J]. Journal of System Simulation，2014，26(5)：1143-1148，1155. (in Chinese)

[13]胡宏德. 基于LabView的汽车运动轨迹跟踪仿真软件开发 [J]. 轻型汽车技术，2013(5/6)：21-23.HU Hongde. Development of Vehicle Motion Trajectory Tracking Simulation Software Based on LabView [J].Light Vehicles，2013(5/6)：21-23. (in Chinese)

[14]李红.自动泊车系统路径规划与跟踪控制研究[D]. 长沙：湖南大学，2014.LI Hong. Research on Controlling of Automatic Parking System in Path Planning and Tracking [D] Changsha：Hunan University，2014. (in Chinese)

[15]韩江，江本赤，夏链，等. 基于轮廓关键点的B样条曲线拟合算法[J].应力数学和力学，2015，36(4)：423-431.HAN Jiang，JIANG Benchi，XIA Lian，et al. B-spline Curve Fitting Algorithm Based on Contour Key Point [J].Applied Mathematics and Mechanics，2015，36(4)：423-431. (in Chinese)