薄板-附加阻尼层复合结构振动模态特性试验研究与仿真分析
王 超,吕振华,顾叶青,吕毅宁
(1.南京电子技术研究所,南京 210039; 2. 清华大学 汽车工程系,北京 100084)
降低车身结构振动与车内噪声水平是提高车辆动态舒适性和客户满意度的重要方法。在汽车的设计与开发中,NVH性能要求贯穿于车身结构设计的全过程。目前多数车身结构都是由薄钢板经冲压焊接而成,该类薄板结构的阻尼损耗因子一般较低,通常只有5×10-3左右[1]。因此,振动响应较大处的车身薄板结构通常还需附加结构阻尼处理,以衰减来自动力总成、排气与传动系统、悬架系统等向车身结构传递的振动,从而通过降低车身薄板的振动来减小车内噪声。
车身等复杂的薄板结构上常用的附加阻尼处理方法包括如图1所示的自由结构阻尼和约束结构阻尼两种形式。结构阻尼的具体处理方式包括粘结型阻尼、热熔型阻尼、喷涂型阻尼、局部约束型阻尼以及复合材料约束阻尼结构等[2-4]。

图1 两种典型的阻尼结构形式
对阻尼层的布置进行优化设计可显著改善车身等薄板结构的振动性能。研究表明,拓扑优化方法是对阻尼结构布置进行优化设计的有效方法[5]。准确获取阻尼材料的力学参数和对薄板-附加阻尼层复合结构进行精确建模是对阻尼结构进行优化设计的基础,王超等[6-7]已对阻尼材料力学参数的测试技术进行了深入研究,本研究重点探讨薄板-阻尼层复合结构的有限元建模技术和分析方法。先对薄板-附加自由阻尼层复合结构的动态特性进行试验分析,再对薄板-附加自由阻尼层复合结构的有限元建模技术进行研究;然后进一步研究了薄板-附加约束阻尼层复合结构的建模技术;最后对薄板-附加阻尼层复合结构的动态特性有限元分析方法进行了深入研究。
1 薄板- 附加自由阻尼层复合结构振动模态试验分析
通过试验分析可以掌握该类薄壁件-附加阻尼层复合结构的基本振动特性,并为薄板-附加自由阻尼层复合结构的有限元分析方法提供试验依据。
1.1 试件设计
车身等薄壁件上附加结构阻尼可以有效改善由车身结构振动(小于200 Hz)引起的车内噪声,据此设计了低阶频率在此频率范围内的两种不同厚度规格的试件。试件1:500 mm×500 mm×0.7 mm薄钢板中央位置粘贴420 mm×420 mm×2 mm的某一热熔型阻尼材料;试件2:500 mm×500 mm×1.6 mm薄钢板的中央位置粘贴420 mm×420 mm×4 mm的某一热熔型阻尼材料。
1.2 试验工况设计
(1)对试件的四个顶点进行固支约束(简称FPGZ)。该约束方式如图2所示,约束试件前应对安装试件的四个加载平台的高度进行调平。

图2 四点固支边界条件下的试验图
(2)对试件的四边进行固支约束(简称FSGZ)。为实现该约束状态,合理设计了一个安装支架,组成安装支架的四个槽钢都是由5 mm厚的钢板折弯而成,该工况下试件的约束形式如图3所示。

图3 四边固支边界条件下的试验图
(3)对试件的两边进行固支约束(简称TSGZ)。将四边固支条件下安装支架的两个短槽钢拆除,即可对试件施加如图4所示的两边固支的约束条件。

图4 两边固支边界条件下的试验图
1.3 测试系统及测点布置
1.3.1 测试系统介绍
试验用PCB333B32单向和PCB356A16三向振动加速度传感器、PCB 086C03力锤、LMS Mobile 05数据采集器等测试设备,建好的测试系统如图2所示。
1.3.2 测点布置
试件上布置了如图5所示的25个测点,试验中为了减小加速度传感器的附加质量对系统的影响,采取了多测点分批次测量的方法。

图5 测点的布置
1.3.3 测试结果分析
试验中对设计的安装支架固有振动特性进行了分析,测得该支架的第一阶固有频率为268.6 Hz,这说明分析两试件在200 Hz以下的振动特性是合适的。此外,由于阻尼材料多用于改善因低频的结构振动引起的振动噪声,所以表1只列出了各边界条件下两试件的低阶固有振动特性。可见,不同的边界条件对薄板-附加自由阻尼层复合结构振动特性的影响较大,四点固支边界条件下,结构的固有振动频率及损耗因子都较低。相对于1.6 mm厚的基础层薄板试件2,0.7 mm厚的基础层薄板的试件1具有更好的耗能特性。产生这种现象的主要原因是基础层薄板厚度较小时,外部的低频激励更容易使其产生较大幅度的运动,在其表面附加自由阻尼层后,阻尼材料通过拉伸变形消耗的振动能量会较大,进而产生较大的模态损耗因子。车身上多数薄板结构的厚度与试件1相近,因此可以认为试件1的耗能特性更接近车身-附加阻尼层复合结构的振动特性。

表1 三种边界条件下两试件的固有振动特性
2 薄板-附加自由阻尼层复合结构有限元建模技术及振动模态计算分析
2.1 有限元建模方法
根据薄板-附加自由阻尼层复合结构的特点,可选用两层偏置板壳单元对其建模[8],该单元通过数值插值方式使两层板壳结构连接表面的变形协调一致。该模型需合理设置板壳单元的法向和偏移量,主要包括以下两种情况:当一层板壳单元的法向指向另一层板壳单元时,偏移量需设为负值;当一层板壳单元的法向背离另一层板壳单元时,偏移量应设为正值。两种情况下偏移量的绝对值都等于板壳单元厚度的一半,建好偏置单元的法向和偏移量后,使两层壳单元在界面处的变形一致,该模型简称为OSOS模型。自由阻尼复合结构另一种常见的建模方法是分别采用偏置板壳单元和六面体单元模拟薄板和阻尼层,两种单元在界面处的变形一致,该模型简称为OSH模型。薄板-附加自由阻尼层复合结构有限元模型的两种建模方法如图6所示。
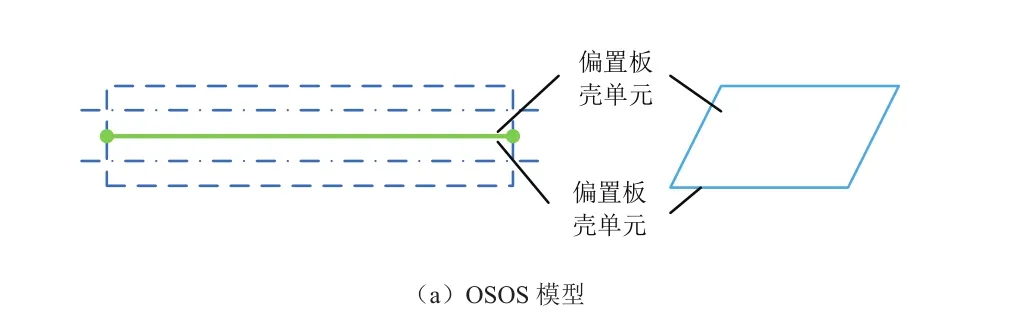

图6 附加自由阻尼层复合结构的两种有限元建模方法
2.2 有限元模型分析精度
以第1.1节中介绍的两种薄板试件的薄板-附加自由阻尼层复合结构为研究对象,并通过振动模态试验结果验证OSOS模型和OSH模型的建模精度。通过模态应变能法(MSE)得到两试件分别在三种边界条件下的模态频率和模态损耗因子,见表2(有限元模型中试件的尺寸按其试验时的工作面积确定)。可见:(1)由于试验固支条件与仿真分析模拟固支条件的差异,试验测量值基本小于仿真值。(2)OSOS模型和OSH模型都有较高的分析精度,但也有各自的特点。OSOS模型具有很高的计算效率和分析精度,但是对某些特殊的边界条件不能客观地进行模拟。如四边固支(FSGZ)中,要求固支基板的边界,而阻尼层的边界不附加外部约束,OSOS模型中难以准确模拟这种边界条件。试验中试件周边不附阻尼材料,仿真分析中同样模拟该边界条件,所以OSOS模型能够较准确地模拟该边界条件,仿真分析结果的精度较高。(3)相对于OSOS模型,OSH模型的计算效率较低(阻尼层为3层实体单元时,其计算时间是OSOS模型的5倍左右),但是其分析精度及适应性好于OSOS模型。

表2 附加自由阻尼层复合结构两种建模方法的精度分析
3 薄板-附加阻尼层复合结构有限元建模与分析技术的进一步探讨
3.1 薄板-附加约束阻尼层结构有限元建模技术
薄板-附加约束阻尼层结构也有多种有限元建模方法,图7列出了三种常见的约束阻尼结构模型,为方便描述,分别简称为OSHOS[9],SRHRS[10],OSBOS[11-12]。OSHOS模型中,薄壁构件和约束层都采用偏置板壳单元构建模型。由于约束阻尼主要靠阻尼层的剪切变形来耗散能量,因此选用六面体实体单元对其进行建模,基板和约束层与阻尼层的接触面通过变形协调关系使这两个接触表面的变形一致,该模型能够反映结构的真实情况,具有较高精度。
SRHRS的基础结构和约束层都采用普通的壳单元建模,粘弹性阻尼层实体单元的上、下表面的两层节点分别与基础层和约束层的壳单元的对应节点通过刚性单元连接,该模型不能准确描述基础层上表面和约束层下表面与阻尼材料表面变形的协调关系。
OSBOS模型采用梁单元来模拟阻尼层,构建一种简单的等效阻尼层模型。梁单元的几何尺寸和材料参数根据壳单元尺寸的大小和阻尼材料的力学特性进行估算,如采用NASTRAN提供的CWELD焊点模型建立这种简化的等效阻尼层模型。该模型与实际约束阻尼结构的差异较大,有明显的缺点。其一,通过一维的梁单元模拟阻尼层结构,不能全面描述阻尼层的变形模式;其二,各梁单元之间的变形关系难以协调;其三,该方法要求研究人员有很强的工程经验,只有这样才能较准确地确定梁单元的参数。

图7 附加约束阻尼层复合结构的三种有限元建模方法
吕毅宁[8]利用OSHOS模型对某一简支的薄板-附加约束阻尼层复合结构进行了建模,并分析其固有振动特性,将分析结果与解析结果进行对比后得出:OSHOS建模方法具有较高的建模精度,且模态应变能法同样适用于约束阻尼层复合结构的设计与分析中;阻尼层实体单元的层数(≥3层)对模型精度的影响较小。
3.2 薄板-附加阻尼层复合结构的动态特性有限元分析方法研究
3.2.1 动态特性有限元分析方法比较
薄板-附加阻尼层复合结构的动态特性有限元分析方法主要包括复特征值法、MSE法及频率响应分析法[13]。这里以第1.1节介绍的四点固支边界条件下的试件1为分析对象,分别采用复刚度法、频率响应法及模态应变能法计算其前2阶的模态频率及损耗因子,三种方法的计算效率对比(同样的硬件条件)见表3。可见,模态应变能法具有最高的计算效率和较高的计算精度;直接频率响应法的计算效率最低,该方法一般多用于计算附加薄板-结构阻尼复合结构的强迫振动响应,当模型规模很大或者激励频率点较多时,可采用计算效率更高的模态频率响应法,但这种基于实模态的模态叠加法的理论体系还不完善,在某些特殊情况下(如模态密集的情形)需要注意分析结果的准确性,也可采用复模态叠加的方法来解决此类问题。

表3 三种分析方法的计算效率对比
3.2.2 模态应变能法分析薄板-附加阻尼层复合结构动态特性的精度
前述分析已表明薄板-附加阻尼层复合结构动态特性的三种分析方法中模态应变能法具有最高的分析效率,且有很高的分析精度,因此该方法得到了广泛的应用。但是,针对模态应变能分析方法的适应性(何种结构特性下具有较高的分析精度)的研究还较少,下面将以一种典型的约束阻尼悬臂梁结构为研究对象,通过理论分析对MSE法的适应性进行初步探讨。
DITARANTO[14]以纵向位移为设计变量推导了约束阻尼梁结构的动力学方程,RAO[15]运用分析力学的方法建立了约束阻尼梁结构的动力学方程。两篇文章中阻尼材料的剪切应变只考虑了因约束层和基础层的横向位移产生剪切应变,从而引起的阻尼层的剪切应变,没有考虑基础层和约束层横截面的转动对其产生的影响,且没有详细介绍约束阻尼梁结构动力学方程的求解方法。MEAD等[16]以横向位移为设计变量详细介绍了约束阻尼梁结构的动力学方程,但是对动力学方程的求解方法没有介绍。本文以约束阻尼梁结构的横向位移为设计变量,分析得到了约束阻尼复合梁结构的通用动力学方程,如式(1)所示,该方程对应的特征方程如式(2)所示。并同时将其固支-固支、自由-自由等常见边界条件以通用的表达式进行了描述,如本例中用到的自由-自由复合梁结构的边界条件如式(3)所示。然后提出了一种单个参数的约束阻尼复合梁结构六阶偏微分动力学方程的求解方法,由于篇幅限制这里不再详细介绍这方面的工作,只将其应用于对MSE法适应性的讨论中。

式中:w为挠度;Y为弯曲模量比;g为剪切模量比;

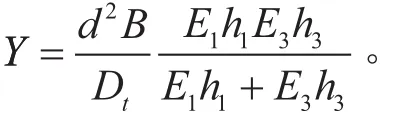
式(1)的解可写成w =Aekxeiωt,则该动力学方程的特征方程为:
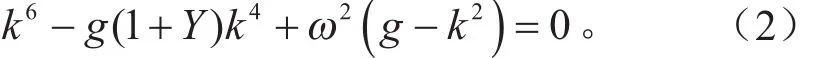
自由-自由复合梁结构自由端边界条件的数学表达为:

如式(2)~(5)所示的自由-自由约束阻尼悬臂梁结构的解析解形式不能显示表达梁结构的固有振动频率f和模态损耗因子ηv,因此采用数值分析的方法对式(2)~(5)进行求解,得到悬臂梁结构的振动特性,这种分析方法在下文中称为半解析法。
以图8所示的附加约束阻尼层复合梁结构(t1=1.0 mm,t2=0.3 mm,t3=0.5 mm,阻尼材料的剪切模量=0.896 MPa)为研究对象。假设阻尼层采用损耗因子为0.1的小阻尼材料,利用MSE法分析其在自由-自由边界条件下该结构的振动特性,分析得到梁结构前四阶弯曲振动的损耗因子和固有频率,如图9所示,并将其分析结果与解析解作对比分析。可以看出,采用MSE法对结构振动特性进行分析具有很高的精度,MSE法求得的结构固有频率与解析结果基本一致;相对而言,MSE法分析得到的第一阶弯曲振动的损耗因子的精度稍低。

图8 约束阻尼层结构示意图
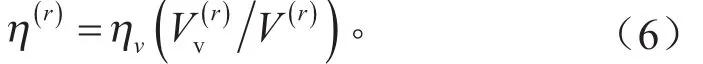
通过模态应变能法的定义式(6)可知,如果阻尼材料的力学参数中只有损耗因子变化,而其它参数都不变,采用该方法对结构进行振动特性分析时,其结构的损耗因子与阻尼材料损耗因子之比为一常数。为了详细分析阻尼材料的损耗因子对结构损耗因子的影响,对该常数关系进行验证,从而进一步确定MSE法的适应性。利用附加约束阻尼层复合梁结构的理论,分析了如图8所示的附加约束阻尼层复合梁结构的振动特性。当采用了不同损耗因子的阻尼材料后,该薄壁梁结构的模态损耗因子与阻尼材料损耗因子的比值变化规律如图10所示,可以得出以下结论:当阻尼材料的损耗因子小于0.8左右时,模态应变能分析方法具有很高的精度,但当材料具有很高的损耗因子时(大于1.0),模态应变能法的分析精度较低;随着阻尼材料损耗因子的增加,约束阻尼复合结构的最大模态损耗因子在较小的剪切参数下即出现,也说明阻尼材料的损耗因子和剪切模量有一个最优的组合关系;当剪切参数较小时,如本例中g' < 10 (G '<2MPa)时,约束阻尼梁结构的损耗因子与材料损耗因子成正比,即该范围内MSE法有较高的分析精度。
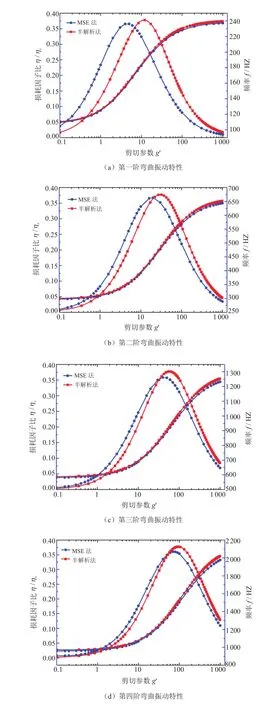
图9 自由-自由约束阻尼梁前四阶弯曲振动特性与剪切参数g'的关系

图10 自由-自由约束阻尼梁模态损耗因子与材料损耗因子的关系
4 结论
(1)通过试验分析了两种规格的薄板-附加自由阻尼层复合结构在四点固支、两边固支和四边固支的三种边界条件下的固有振动特性,在此基础上,研究了附加自由阻尼层复合结构有限元模型建模技术,并通过试验验证了所建立的有限元模型的精度。在薄板-附加自由阻尼层复合结构建模技术的基础上,进一步探讨了薄板-附加约束阻尼层复合结构的有限元模型建模技术。
(2)分析了薄板-附加阻尼层复合结构动态特性的三种有限元分析方法的精度及适用分析工况,并通过理论分析的方法对得到广泛应用的MSE法的适应性进行了研究。分析认为当阻尼材料的损耗因子较小时(小于0.8),MSE法具有很高的分析精度,但当材料的损耗因子较大时(大于1.0),MSE法的分析精度则较低。
参考文献(References):
[1]庞剑,谌刚,何华. 汽车噪声与振动——理论与应用[M].北京:北京理工大学出版社,2006.PANG Jian,CHEN Gang,HE Hua. Automotive Noise and Vibration—Principle and Application [M]. Beijing:Beijing Institute of Technology Press,2006.(in Chinese)
[2]ROY N,GERMÈS S,LEFBVRE B,et al. Damping Allocation in Automotive Structures Using Reduced Models[C]//International Seminar on Modal Analysis(ISMA),France,2006.
[3]SUBRAMANIAN S,SURAMPUDI R,THOMASON K R,et al. Optimization of Damping Treatment for Structure Borne Noise Reduction[C]//SAE Technical Papers,2003-01-1592,2003.
[4]RAO M D. Recent Applications of Viscoelastic Damping for Noise Control in Automotive and Commercial Airplanes [J]. Journal of Sound and Vibration,2003,262:457-474.
[5]吕毅宁,吕振华,赵波,等. 附加自由阻尼结构系统的有限元分析和拓扑优化设计方法研究[J].计算力学学报,2012,19(2):178-183.LYU Yining,LYU Zhenhua,ZHAO Bo,et al. A Finite Analysis and Topology Optimization Method for Structures with Free Damping[J].Chinese Journal of Computational Mechanics,2012,19(2):178-183.(in Chinese)
[6]王超,吕振华,钟剑锋. 识别粘弹性材料力学参数的自由阻尼试件设计方法研究[J].应用力学学报,2016,33(4):582-588.WANG Chao,LYU Zhenhua,ZHONG Jianfeng. Research on Design Methods of Free Damping Specimens Used in Measurement of Viscoelastic Material’s Mechanical Parameters[J].Chinese Journal of Applied Mechanics,2016,33(4):582-588.(in Chinese)
[7]王超,吕振华,顾叶青. 识别粘弹性阻尼材料力学参数用约束阻尼试件设计方法[J].中国机械工程,2016,27(9):1208-1214.WANG Chao,LYU Zhenhua,GU Yeqing. Design Methods of Sandwich Specimen Used in Measurement of Viscoelastic Damping Material’s Mechanical Parameters[J].Chinese Journal of Mechanical Engineering,2016,27(9):1208-1214. (in Chinese)
[8]吕毅宁.车身结构刚度和振动特性设计分析的几个关键问题研究[D]. 北京:清华大学,2008.LYU Yining. Researches on Several Key Problems of Design and Analysis of Automotive Body Stiffness and Vibration Characteristics[D]. Beijing:Tsinghua University,2008. (in Chinese)
[9]SUN C T,LU Y P. Vibration Damping of Structural Elements[M]. New Jersey:Prentice Hall,1995.
[10]ETIENNE B,SYLVAIN G. Tools for Viscoelastic DampingTreatment Design:Application to an Automotive Floor Panel[C]//International Seminar on Modal Analysis(ISMA),Leuven,2002.
[11]LU Y P,CLEMENS J C,ROSCOE A J. Vibrations of Composite Plate Structures Consisting of a Constrained-layer Damping Sandwich with Viscoelastic Core[J]. Journal of Sound and Vibration,1992,158(3):552-558.
[12]KILLIAN J W,LU Y P. A Finite Element Modeling Approximation for Damping Material Used in Constrained Damped Structures[J]. Journal of Sound and Vibration,1984,97(2):352-354.
[13]MSC Software Corporation. MSC Nastran Version 70 Advanced Dynamic Analysis User’s Guide[Z]. 2004.
[14]DITARANTO R A. Theory of Vibratory Bending for Elastic and Viscoelastic Layered Finite-length Beams[J].Journal of Applied Mechanics,1965,32(4):881-886.
[15]RAO D K. Frequency and Loss Factors of Sandwich Beams Under Various Boundary Conditions[J]. Journal of Mechanical Engineering Science,1978,20 (5):271-282.
[16]MEAD D J,MARKUS S. The Forced Vibration of a Three-layer,Damped Sandwich Beam with Arbitrary Boundary Conditions[J].Journal of Sound and Vibration,1969,10(2):163-175.

