山区公路弯道路段汽车最小轨迹半径分布特性

胡正云，王 灿

（1.安徽交通职业技术学院，合肥 230022；2.重庆交通大学，重庆 400074）

驾驶行为是人、车、路等要素耦合而成的系统输出，这种输出具体由行驶速度与行驶轨迹协同表征。速度参数影响车辆纵向的行驶安全性，而行驶轨迹则对车辆的侧向安全性影响显著。直线路段行驶时，驾驶员普遍倾向于沿道路中心线行驶，而弯道路段行驶时，驾驶员的行驶轨迹究竟体现何种规律，与实际的道路线性参数如何耦合互动，都是亟待解决的科学命题。

国外学者对汽车行驶轨迹方面的研究主要集中在轨迹检测，以及道路几何参数与行驶轨迹的耦合规律等方面。SPACEK[1]利用红外线观测柱所测数据通过计算机程序计算出车辆行驶轨迹，并根据车辆行驶工况划分出6类行驶轨迹。IMRAN等[2]提出了基于行驶轨迹坐标数据对车辆进行控制的方法。DISSANAYAKE等[3]通过分析车辆流量、轨迹偏差等采集参数，发现道路交通特征对车辆行驶轨迹影响显著。

国内学者对汽车行驶轨迹方面的研究主要集中在公路曲线段的车辆行驶轨迹、轨迹特性、人-车-路协同轨迹决策等方面。杨轸[4]在综合考虑道路线性、驾驶环境、交通设施、人为因素等基础上，建立了驾驶员-汽车闭环模型，对汽车在进入曲线段时发生的轨迹偏移进行了研究。

林雨等[5]以车辆行驶在双车道公路弯道为前提，发现车辆在出入曲线段行驶轨迹的运动偏移趋势方面存在显著的差别。任园园[6]以弯道交通行为为对象，从心理决策角度研究驾驶行为和车辆行驶轨迹，并以大量试验数据为基础，给出了不同弯道上行驶轨迹的描述方程，为研究弯道行车安全与行驶轨迹提供参考。徐进等[7]针对驾驶员驾驶习惯、典型驾驶建立了目标函数，根据不同的公路特点，设置了相应的约束条件，并参考驾驶员决策过程，建立了基于人-车-路协同的行驶轨迹决策模型。

综上所述，国内外学者对车辆行驶轨迹的研究主要集中在道路几何参数、公路曲线段行驶轨迹、人-车-路协同轨迹决策等方面，对山区弯道安全方面的研究则较少。但是在实际驾驶过程中，驾驶员由于心里因素（如认为路径最短则时间最短）或驾驶习惯的不同，会在弯道行驶时采取紧贴道路内侧行驶，从而产生较大的安全隐患，尤其在线型复杂多变的山区弯道路段更易发生事故。因此，车辆行驶安全与行驶轨迹的最小半径存在何种关联，山区双车道路段行驶轨迹存在何种特征均亟待解决。针对上述情况，本文采用GPS技术获取驾驶员行驶轨迹参数，提取出行驶轨迹最小半径rmin，找出不同弯道行驶半径与最小半径差值Q分布规律，为研究山区道路行驶轨迹安全提供参考。

1 车辆行驶轨迹的形成

在驾驶员实际驾驶过程中，路况因素（如周围环境状况）和人为因素（如驾驶员心理素质和驾驶习惯）都会导致车辆行驶呈现多样性，下文将对上述影响因素进行分析。

路况因素主要分为道路几何特性、路面状况、周围车辆行驶状况以及道路上突然出现的干扰等4个方面。这4个方面既对车辆行驶轨迹造成不同影响，又有很强的交互性，起到共同约束的作用。

在人为因素方面，车辆的行驶轨迹反映了驾驶员在驾驶过程中的选择行为，由驾驶员的驾驶习惯或心理素质决定。主要分为以下4种情形：第1种为距离最优，此类驾驶员普遍存在“距离最短，油耗最少”的认知，在驾驶中尤其在弯道处常采取紧贴路段内侧行驶，行驶轨迹通常呈切弯现象，在山区弯道上更为明显。第2种为时间最优，此类驾驶员往往对所驾车辆的动力性能较为熟悉，精于车辆控制，在不同道路线性下，都能快速平稳地通过弯道，这体现在驾驶员在入弯处和出弯处放缓轨迹半径，使车辆的行驶时间最短。第3种为转向操纵最优，此类驾驶员在车辆驾驶方面不熟练，因而驾驶车辆时较为紧张，为缓解紧张情绪，在满足过弯转动角度的前提下，采取减少方向盘角输入以降低驾驶负荷。第4种为安全最优，此类驾驶员属于保守驾驶，在山区悬崖等弯道路段，为避免车辆驶出安全车道，采取居中行驶来确保离右端路缘有足够的安全距离。由于实际驾驶过程中的道路上干扰因素过多，上述典型驾驶情形一般不会单独出现，而是以相互耦合的形式共同影响驾驶员的驾驶行为。

综上所述，车辆行驶轨迹的形成要受两方面因素的制约：一方面是驾驶员受行驶环境等路况因素共同约束的影响；另一方面受驾驶员驾驶习惯和心理素质差异的影响，体现在对上述4种驾驶情形所做的抉择差异。因此，不同驾驶员驾驶的车辆行驶轨迹呈现多样化，差值Q普遍存在。根据实车试验数据，绘制了驾驶员两种常见的通过弯道示意图，如图1所示。

图1 驾驶员两种常见过弯示意图

2 车辆行驶轨迹最小半径rmin

经研究发现，车辆在某弯道的侧向加速度与轨迹曲率和行驶速度存在着一定的数学关系。

式中：ayi为侧向加速度；vi为车辆行驶速度；ki为行驶轨迹曲率。

根据实车试验数据和引入数学公式计算出车辆轨迹曲率等数据，并绘制成曲线图。为避免实车试验中偶然因素对试验结果的影响，对同一条路段进行多次测量以求取平均值的方法来减小误差，确保数据的准确性。车辆侧向加速度和轨迹曲率曲线随时间变化的走势基本保持一致，如图2所示。当曲线处于峰值时，汽车的稳定性和平顺性都会大打折扣。

图2 车辆行驶参数曲线图

人们在研究汽车弯道安全时，一般以弯道平曲线中线的半径为参数来构建汽车弯道安全模型，并得出弯道半径越小，汽车发生事故率越大的结论。但汽车在实际转弯过程中，车辆行驶轨迹曲率存在波动，这表明在实际驾驶情形中，车辆不会完全沿着山区弯道中线行驶，车辆行驶轨迹与实际道路中线存在一定的偏离，套用固定的弯道道路中线半径作为参数建立汽车弯道安全模型有一定的安全风险，如图2b所示。因此本文结合汽车弯道行驶的真实情况，采用车辆的实际行驶轨迹最小半径 （即最大轨迹曲率值的倒数）作为评价车辆行驶安全性的参数，并以此参数来建立道路交通安全预测模型。

3 弯道路段rmin分布特征

由图3可知，汽车行驶轨迹的最小半径rmin和弯道半径R之间存在差值。把汽车弯道平曲线半径与汽车行驶轨迹最小半径之差定义为差值Q，并以此来分析汽车弯道行驶轨迹最小半径的分布特征。

根据几何关系可得：

对实车试验数据进行分析时，发现在不同的弯道半径范围内，rmin存在一定差异，为保证结果可靠，把弯道平曲线半径分成3个区间（0～100 m、100～200 m、200 m以上）进行研究。

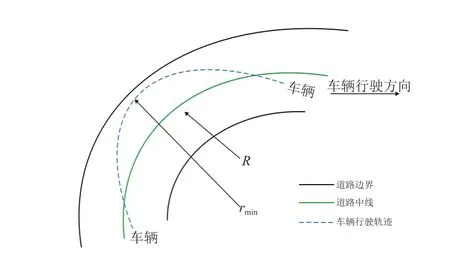
图3 轨迹最小半径与弯道半径偏差示意图

3.1 0～100 m区间的rmin分布特征

Q通过整合试验数据，得到表1、表2和表3。由表1可知，当平曲线半径在0～100 m区间时，平曲线的转角范围为49°～169°，行驶轨迹最小半径区间为9.02～88.65 m，差值Q的取值区间为-3.17～43.39 m。

表1 平曲线半径0～100 m区间内最小行驶半径分布特性

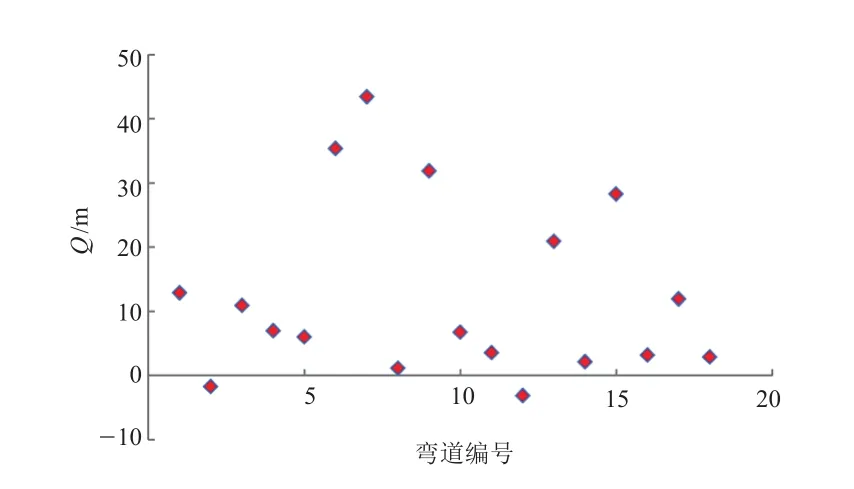
图4 弯道半径0～100 m的Q值分布图

3.2 100～200 m区间的rmin分布特征

由表2可知，当平曲线半径在100～200 m区间时，平曲线的转角范围为22°～99°，行驶轨迹最小半径区间为96.48～177.05 m，差值Q的取值区间为0.51～20.17 m。

绘制当前范围弯道Q值与弯道序号的散点图，如图5所示。由图可知，Q值较为集中，且取值区间为0～20.17 m。

以Q值为纵坐标，弯道序号为横坐标，绘制Q值与弯道序号的散点图，如图4所示。由图可知，Q值比较分散。

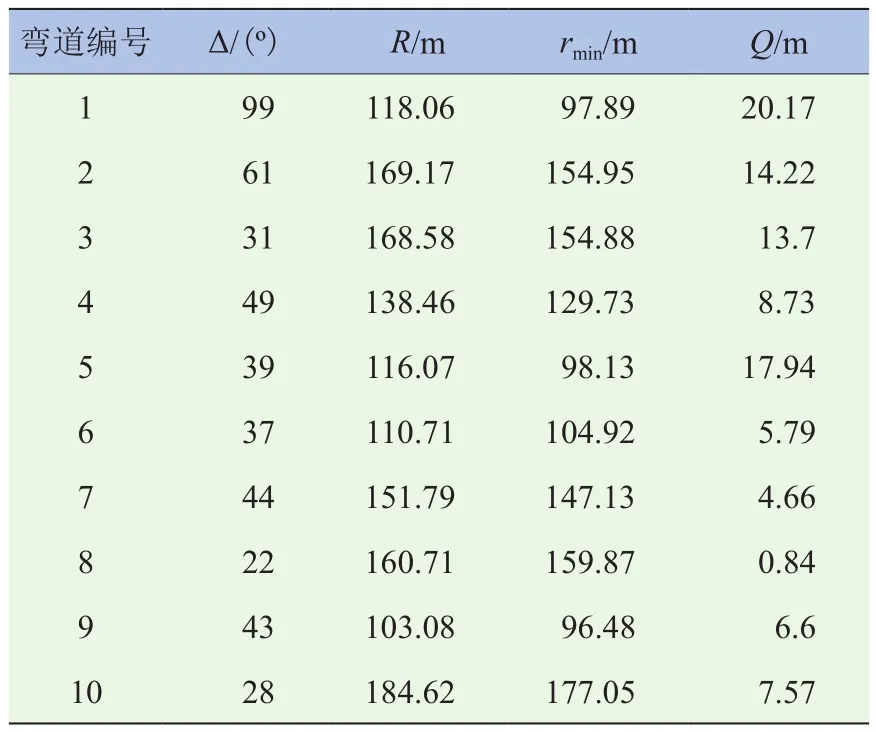
表2 平曲线半径100～200 m区间内最小行驶半径分布特性

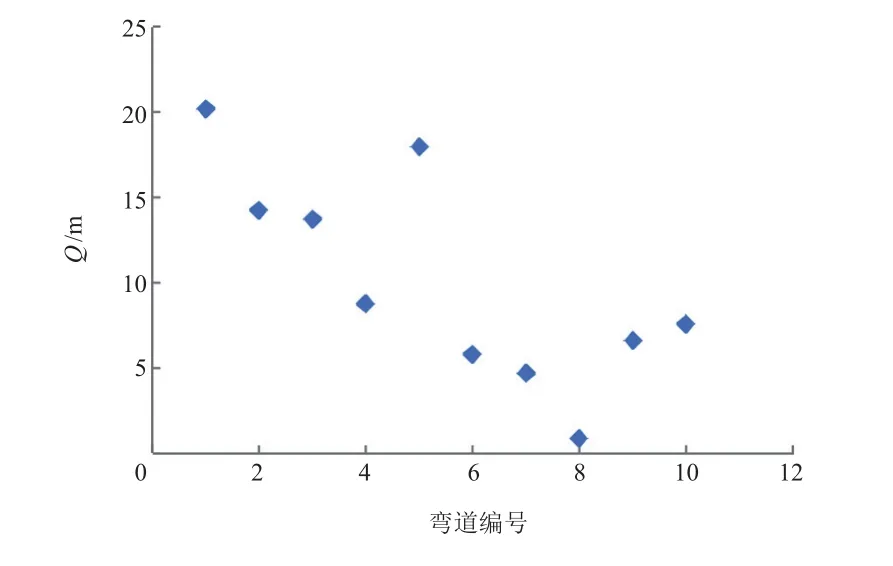
图5 弯道半径100～200 m的Q值分布图

3.3 200 m以上区间的rmin分布特征

由表3可知，平曲线半径在200 m以上区间时，平曲线转角范围为26°～63°，车辆行驶轨迹区间为205.36～353.9 m，Q的取值区间为1.92～9.59 m。

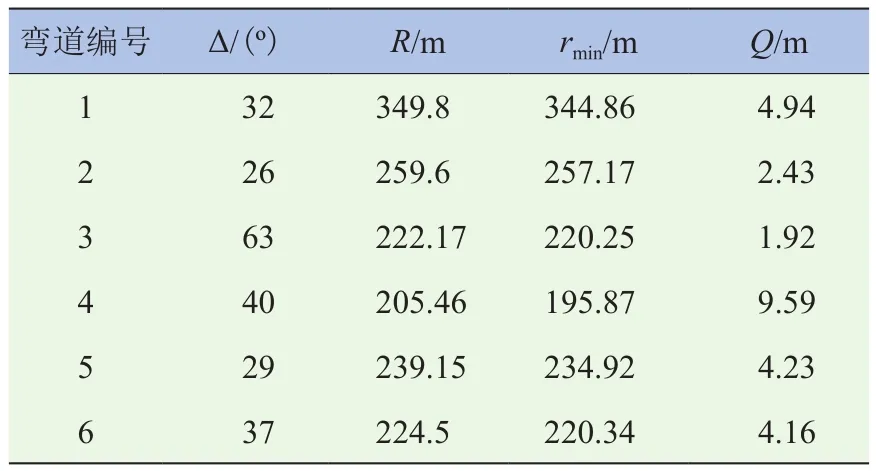
表3 平曲线半径大于200 m时最小行驶半径分布特性

绘制当前范围弯道Q值与弯道序号的散点图，如图6所示。由图可知，Q值分布较集中，且取值区间为1.92～9.59 m。

综上所述，在不同半径范围内的平曲线，Q值存在一定差异，因此，汽车不会沿着弯道道路中线行驶。当弯道半径范围在0～100 m时，Q值分布较分散且Qmax较大；当弯道半径范围在100～200 m和200 m以上时，Q值分布较集中且Qmax较小。

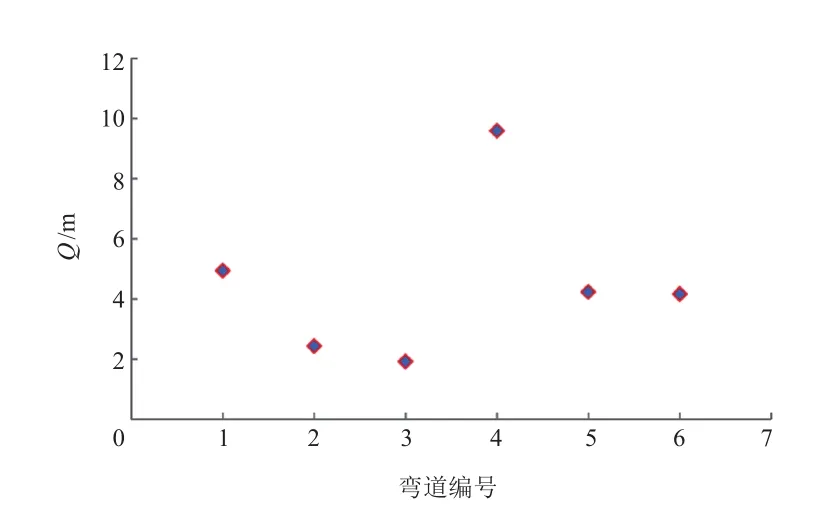
图6 弯道半径200 m以上的Q值分布图

4 结论

本文首先探讨了人和路况方面因素对汽车行驶轨迹的影响，发现各类影响因素呈现较强的交互性，共同约束汽车行驶轨迹的生成。绘制了车辆在道路上的两种典型过弯示意图，分析所采集的数据，发现驾驶员驾驶车辆的行驶轨迹与弯道半径普遍存在差异，若以弯道道路中线半径作为参数建立汽车弯道安全模型有一定安全风险。因此，提出了以车辆行驶轨迹最小半径rmin作为衡量车辆行驶安全性标准的研究思路。对不同弯道半径路段进行数据统计后发现：当汽车行驶弯道半径的区间为0～100 m时，Q值分布较分散且Qmax较大；当行驶弯道半径区间为100～200 m或200 m以上时Q值分布区间为0.52～19.63 m和1.8～9.1 m，由此得出Q值随着弯道半径增大，其离散程度逐渐减小的结论。

参考文献（References）：

[1]SPACEK P. Track Behavior in Curve Areas：Attempt at Typology [J]. Journal of Transportation Engineering，2005，131(9)：669-676.

[2]IMRAN M，HASSAN Y，PATTERSON D. GPS-GISBased Procedure for Tracking Vehicle Path on Horizontal Alignments [J]. Computer-aided Civil and Infrastructure Engineering，2006，21(5)：383-394.

[3]DISSANAYAKE S，LANDMAN D，RUSSELL E R，et al. Effect of Longitudinal Joints on Vehicle Positioning[C]// 4th International Symposium on Highway Geometric Design，June 2-5，2010，Valencia，Spain.

[4]杨轸. 行车动力学仿真模型研究 [D]. 上海：同济大学，2004.YANG Zhen.Research of Vehicle Dynamics Simulation Model [D]. Shanghai：Tongji University，2004.(in Chinese)

[5]林雨，牛建峰，徐颖. 双车道公路弯道行车轨迹特性研究 [J]. 公路交通科技，2011，28 (3)：113-117.LIN Yu，NIU Jianfeng，XU Ying. Study on Lane Trajectory Characteristics of Two Lane Highway [J]. Journal of Highway and Transportation Research and Development，2011，28 (3)：113-117.(in Chinese)

[6]任园园. 公路弯道路段行车危险区域及驾驶行为模型研究 [D]. 长春：吉林大学，2011.REN Yuanyuan. Study on Curved Section Highway Dangerous Area and Driving Behavior Model [D].Changchun：Jilin University，2011.(in Chinese)

[7]徐进，赵军，邵毅明，等. 基于“人-车-路”协同的复杂公路/赛道行驶轨迹决策模型 [J]. 系统工程理论与实践，2014，34(5)：1311-1323.XU Jin，ZHAO Jun，SHAO Yiming，et al. Decision Model of Complex Highway/Track Based on Human Vehicle Road Coordination [J]. System Engineering Theory and Practice，2014，34 (5)：1311-1323.(in Chinese)