单太阳翼放气干扰力矩分析

边志强 王鑫 栗双岭 董瑶海 沈毅力 曾擎 洪振强 宋效正

(1 上海卫星工程研究所,上海 201109)(2 中国卫星海上测控部,江苏江阴 214431)(3 上海航天技术研究院,上海 201109)

放气现象在卫星中普遍存在，如微波部件为防止空间低气压放电一般都设计放气孔，卫星推进管路在发射过程中会根据程序控制打开阀门进行管路放气[1]，卫星结构中广泛应用的蜂窝夹层板、隔热材料、胶黏剂等材料在真空、高低温、粒子辐射等环境中蒸发、升华和分解释放出气体，这不仅影响材料本身的性能，还会对光学仪器等造成污染，甚至还会使姿态产生显著变化。

目前，国内外都有针对卫星在轨干扰力矩辨识的研究，文献[2-3]中以“国际空间站”为例，分析了飞船压力舱壁受微小陨石和空间碎片撞击出现漏气小孔，提出漏气小孔的喷气产生干扰力矩，引起飞船姿态显著变化，利用非线性滤波方法估计干扰力矩大小，但是该方法需要精确知道干扰力矩初值，而实际在轨时初值是很难精确得到的。文献[4]针对卫星稳态下的运动，提出了一种基于特征系统实现算法的卫星周期干扰力矩估计方法，但是该方法仅应用于卫星稳态飞行时干扰力矩的估计；文献[5]中针对轴对称卫星提出了一种利用发动机喷气过程角速度变化解算干扰力矩的方法，该方法在角速度较小时效果比较好，而且仅针对轴对称航天器。

太阳翼的放气模型很难建模，并且地面无法测试扰动力矩大小。卫星在轨运行时，太阳翼放气干扰力矩很难直接测量，可通过测量其他物理参数进行间接估计。在轨实际估计太阳翼放气干扰力矩，一方面可以及时修正控制参数，避免姿态频繁振荡，减少推力器频繁工作和燃料过多消耗；另一方面，在轨估计数据可以作为后续卫星姿轨控设计输入，进行推力器控制设计时可以放宽极限环阈值，根据放气程度逐渐减弱采用阈值更小的控制极限环。本文首先给出太阳翼放气以及影响卫星姿态的机理，推导利用卫星姿态动力学模型、姿态变化和推力器等参数估计太阳翼放气产生的干扰力矩过程，最后以风云四号(FY-4)卫星转移轨道段太阳翼对日定向过程为例，进行了理论模型的验证，在轨实时估计太阳翼放气力矩。

1 太阳翼在轨放气机理

文献[6-9]的相关研究表明，真空下气体放气是随时间以负指数衰减，放气率与时间关系可以描述为q=A·exp(-t/B)，其中q为材料放气率，A、B为放气时间常数。文献[10]中根据实验数据拟合，得到的放气速度表达式与理论分析的放气负指数函数一致，说明了放气速率过程的负指数函数模型的正确性。具体的放气指数模型不是本文研究重点，不再进行深入研究。

太阳翼基板为碳纤维复合材料网格面板/铝蜂窝芯夹层刚性结构，由碳纤维复合材料网格面板、铝蜂窝芯、铰链支座、聚酰亚胺薄膜等组成。蜂窝芯夹层由面板、蜂窝芯子和胶黏剂构成[11](见图1)。由于地面制造和储存使蜂窝夹层内含大量空气，在低于0.01 Pa的空间环境下，蜂窝夹层内压力增大，在材料表面上吸附的气体从表面脱附，溶解于材料内部的气体向真空边界扩散，最后在界面上释放、脱离材料，气体分子不断从其表面脱离释放出来并挥发逸出，最终达到蜂窝内腔和外界的压力平衡。根据理论模型可知，在放气初阶段放气速率较快，但随着时间衰减速率逐渐减小，趋于平稳。在发射主动段，星体、太阳翼也进行放气，但主动段时外界有一定大气压力，对放气速率有阻碍作用，且主动段不具备放气速率和干扰力矩分析的条件。本文只研究星箭分离后，太阳翼对日定向过程中的放气影响。

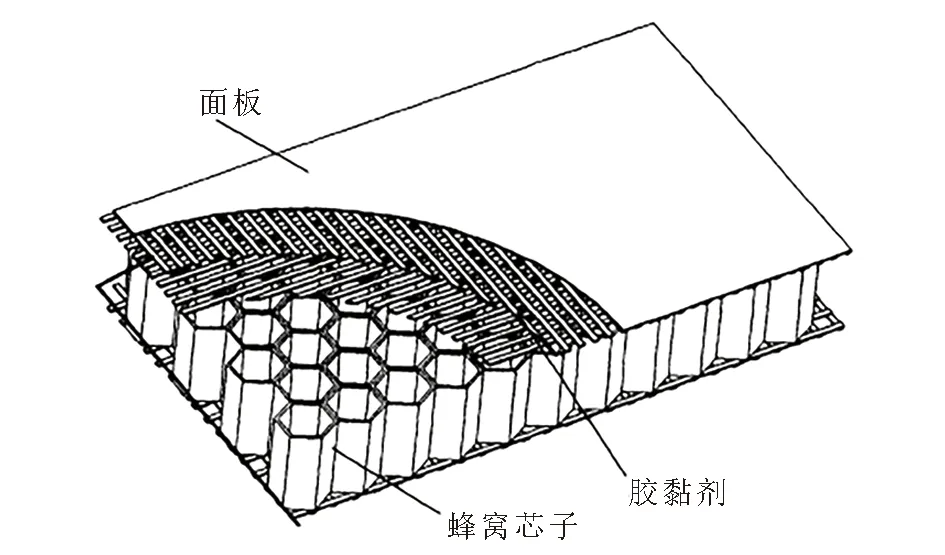
图1 太阳翼蜂窝芯夹层结构示意图Fig.1 Honeycomb sandwich interface schematic of solar wing

2 太阳翼放气干扰力矩估计

估计静止轨道卫星转移轨道段太阳翼放气干扰力矩时，空间环境干扰力矩很多，如重力梯度力矩、太阳光压力矩、推力器羽流等，这些对太阳翼放气干扰力矩的估计影响较小，分析如下：

(1)重力梯度力矩是周期性的，而本文估计的在轨放气干扰力矩无周期性，此重力梯度力矩可以不考虑；推力器羽流影响只发生在推力器喷气时刻，而在非喷气时是对星体无干扰的，与在轨干扰力矩长时间持续存在现象不一致，可以忽略羽流影响。

(2)非对称构型卫星的单太阳翼放气力矩对卫星姿态变化影响较大，而双太阳翼的对称结构，放气力矩为力偶模式，部分相互抵消，不容易被测量估计。本文只针对单太阳翼卫星的放气情况进行分析。

(3)卫星在轨飞行过程中，姿态受到太阳光压力矩、重力梯度力矩和气动力矩的影响，椭圆轨道和静止轨道卫星轨道特性决定了气动力矩、重力梯度力矩方向不断随轨道周期性变化，并且持续时间较短。因此，在估计太阳翼放气力矩时，可忽略重力梯度力矩和气动力矩的影响。

作用在整个航天器上的光压力矩Msun[12]为

Msun=-∬Sρsuncosθ[(1-η)L+2ηcosθn]dS

(1)

式中：L为辐射源方向的单位矢量；0≤η≤1为航天器表面的反射系数；n为受照表面的法向单位矢量；ρsun是受照面处的光压强度，ρsun=I0/c(I0为太阳辐射通量，c为光速)；θ是受照面法向单位矢量与辐射源方向单位矢量之间的夹角；积分区域S表示遍及航天器承受光压力的表面部分。

以静止轨道卫星为例，取I0=1358 J/m2，η=0.9，θ=0°，积分有效区域S取(17～30)m2。则可计算出太阳翼对日定向过程中，单太阳翼的光压力矩Msun值在0.2 mN·m～0.4 mN·m范围，这个量级的干扰对卫星姿态影响较小，在进行放气干扰力矩估计时可以忽略太阳光压力矩的影响。

本文的卫星本体坐标系Ob-XbYbZb定义为：坐标原点Ob(卫星质心)，ObXb轴、ObYb轴和ObZb轴为卫星的3个几何轴；太阳翼本体坐标系Op-XpYpZp定义为：坐标原点Op(太阳翼安装点)，OpXp轴、OpYp轴和OpZp轴为太阳翼本体的3个几何轴(见图2)。卫星在对日定向巡航阶段时，太阳翼不转动，太阳翼电池片贴片面的法线与太阳光入射方向恰好相反。太阳翼基板的放气孔在电池片贴片面的背面，放气产生的反作用力与太阳翼电池片贴片面的法线一致，结合整星质心位置，可知太阳翼放气作用力产生的扰动力矩在卫星本体坐标系+Xb轴方向，对卫星+Xb轴姿态角速度和姿态角有较大影响。

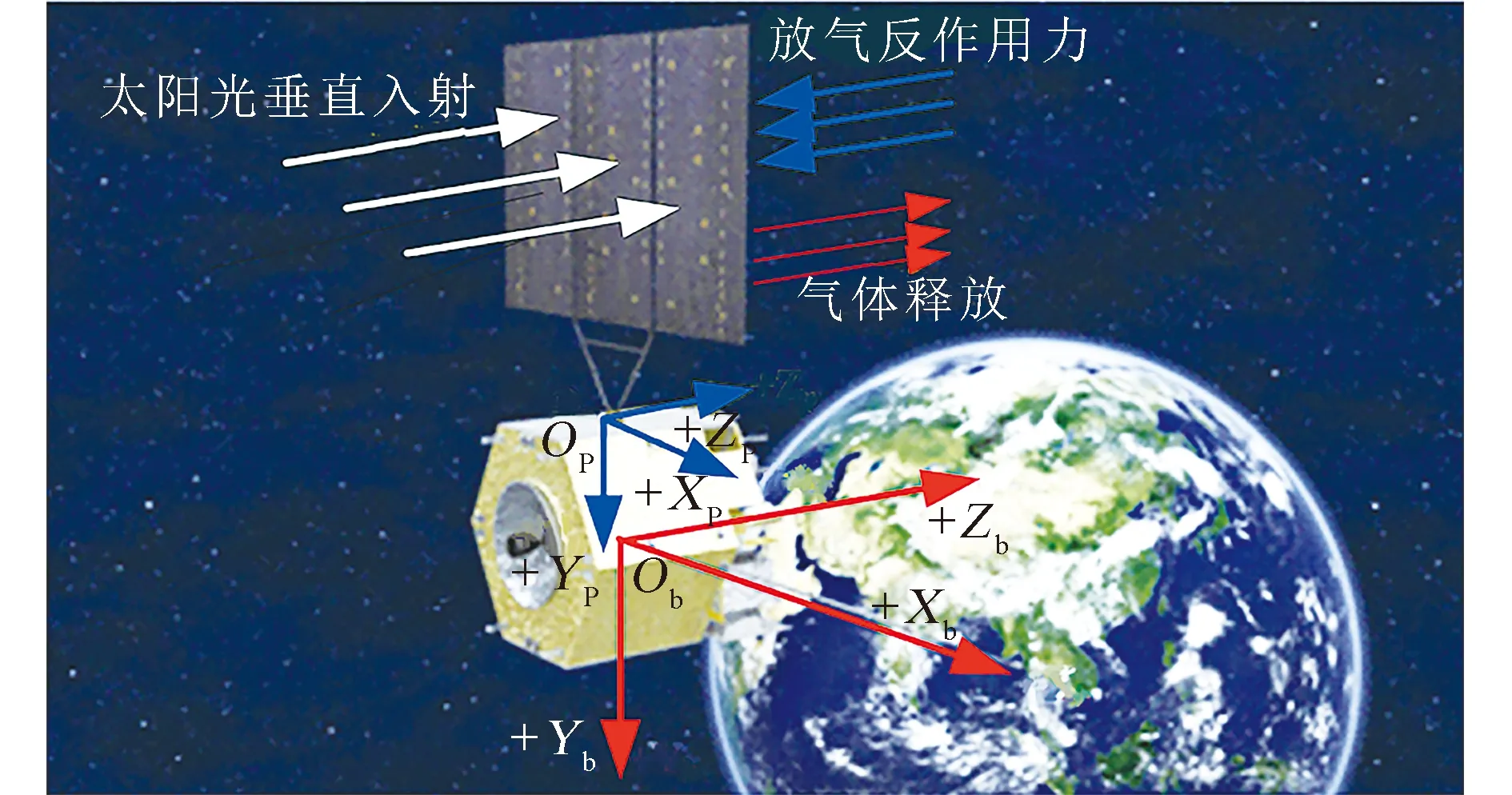
图2 卫星太阳翼在轨放气方向示意图Fig.2 Air-bleed of solar wing schematic

2.1 带干扰力矩的卫星动力学方程

卫星在转移轨道段对日巡航状态下，太阳翼放气产生的干扰力矩是长时间持续存在的，对姿态的扰动通过陀螺测量得到角速度实时数据，进而输入到姿态轨道控制计算机中，解算姿态控制推力器的工作状态从而进行控制。卫星姿态动力学方程为

(2)

式中：J为卫星转动惯量矩阵，ω为卫星惯性角速度，Mc为推力器控制力矩，Md为卫星受到的干扰力矩。姿态动力学方程中，转动惯量可以在地面精确测量得到，姿控推力器控制力矩根据推力器安装位置、推力大小和方向可以计算得到，卫星实时角速度利用陀螺可以测量得到。

(1)卫星转动惯量：卫星在不同轨道阶段、不同部件展开状态下的转动惯量，可在地面通过理论计算和试验测试得到精准的数据，误差在0.1%以内[13]。星箭分离后，用于姿态控制的燃料消耗较少，忽略整星质心的变化，认为此过程转动惯量保持不变。

(2)推力器控制力矩：卫星巡航过程中的控制力矩由固定推力大小和方向不变的姿控推力器产生，Mc=L×F，L表示推力力臂，为卫星质心到推力作用点的向量，F为推力器工作推力。力臂L可以在地面精确地测量得到，且估计过程中保持不变。推力F在初始变轨阶段认为保持不变。因此，控制力矩Mc可以较为准确的计算得到。

(3)卫星姿态角速度解算：卫星惯性角速度通过陀螺表头构型以及各个接入系统陀螺的角速度测量输出。根据陀螺表头实际安装指向，用矩阵A3×N描述陀螺安装矩阵。实际在轨运行时，选取其中5个陀螺表头的输出值解算卫星惯性角速度，即

(3)

式中：A3×5为选取的5个表头的安装矩阵，ωxb、ωyb、ωzb为惯性系相对于卫星本体坐标系的三轴角速度，ωgi(i=1,2,3,4,5)为选取表头的测量值，为惯性系相对于陀螺测量轴的三轴角速度。

2.2 太阳翼放气干扰力矩计算

卫星姿态动力学方程表示如下：

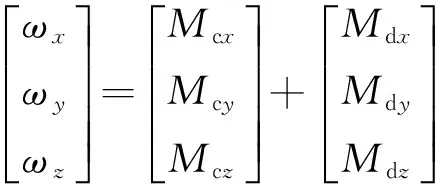
(4)

式中：Jxx、Jyy、Jzz为卫星转动惯量的主惯量，Jxy、Jzx、Jyz为卫星转动惯量的惯性积；ωx、ωy、ωz为卫星三轴惯性角速度在本体系中的分量；Mcx、Mcy、Mcz为卫星在本体系下受到的三轴控制力矩；Mdx、Mdy、Mdz为卫星在本体系下受到的三轴干扰力矩。

惯量积相对主轴惯量较小，且经仿真计算知其影响很小可忽略不计，而角速度耦合项干扰力矩估计中不能忽略不计。因此，动力学方程简化表示为

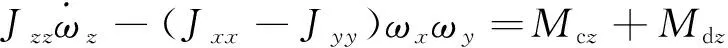
(5)

对式(4)[t0,t0+T]时间内进行积分(T为积分时间)，对于其它坐标轴与本轴的耦合项，采用数值积分的方法，以陀螺角速度更新周期Tg(一般为0.5 s，满足T=kTg，k为整数)为步长，在整个积分时长内进行积分求和。

(6)

控制力矩分为正向控制力矩和负向控制力矩，近似为恒定值。滚动轴控制力矩为Mcx+、Mcx-，推力器工作时长为Δtx+、Δtx-；俯仰轴控制力矩为Mcy+、Mcy-，推力器工作时长为Δty+、Δty-；偏航轴控制力矩为Mcz+、Mcz-，推力器工作时长为Δtz+、Δtz-。卫星遥测数据下传各方向推力器工作时长为Δti、Δti-(i=x,y,z)。太阳翼放气干扰力矩在整个过程中一直存在，而且变化缓慢。为了保证太阳翼放气干扰力矩估计时效性，积分步长选取为秒量级的，认为在积分时长T内是不变化的。因此，在[t0,t0+T]时间内，有

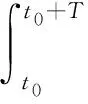
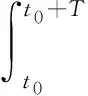
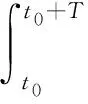
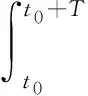
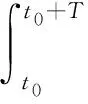
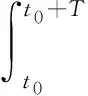
(7)

因此，由式(5)～式(7)可以表示为

(8)

利用式(8)可以计算得到太阳翼放气干扰力矩。

根据在轨数据需求确定得到迭代步长T1，每隔T1时长，取一个点作为本次积分的t0时刻，利用上述方法可以计算得到连续放气干扰力矩。干扰力矩实时连续估计实施流程分为4步(见图3)：第一步，采集卫星角速度和推力器时间数据；第二步，确定相关时间参数；第三步，积分求和；第四步，解算放气干扰力矩。

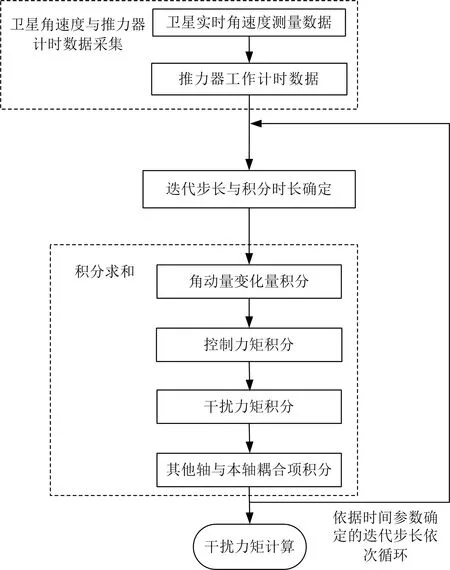
图3 干扰力矩估计流程图Fig.3 Flow chart of disturbance torque estimation

3 太阳翼放气干扰力矩估计

3.1 理论仿真计算

以FY-4卫星参数为例，模拟转移轨道段单太阳翼对日定向过程，估计太阳翼放气干扰力矩。太阳翼展开后卫星惯量矩阵(单位：kg·m2)为

(9)

推力器产生Xb轴控制力矩Mcx+=Mcx-=18.9 N·m，产生Yb轴控制力矩Mcy+=Mcy-=19.75 N·m，产生Zb轴控制力矩Mcz+=Mcz-=15.4 N·m。陀螺角速度更新周期Tg为0.5 s，推力器工作计时更新周期以及积分步长T=16 s。为保证数据时效和数据量适中，迭代步长T1=16 s。卫星动力学模型中，光压力矩模型采用式(1)模型和相关参数，并人为模拟了太阳翼放气干扰力矩，其模型为Mdx=0.05·exp(-0.000 2·t)。仿真过程中采用与星上一致的开关线推力器控制规律，姿态角与姿态角速度的控制阈值分别为0.5°、0.004 5(°)/s。陀螺测量误差为0.005(°)/s，太阳敏感器测量噪声为0.1°。根据前述算法进行太阳翼放气干扰力矩估计，估计结果如图4所示。

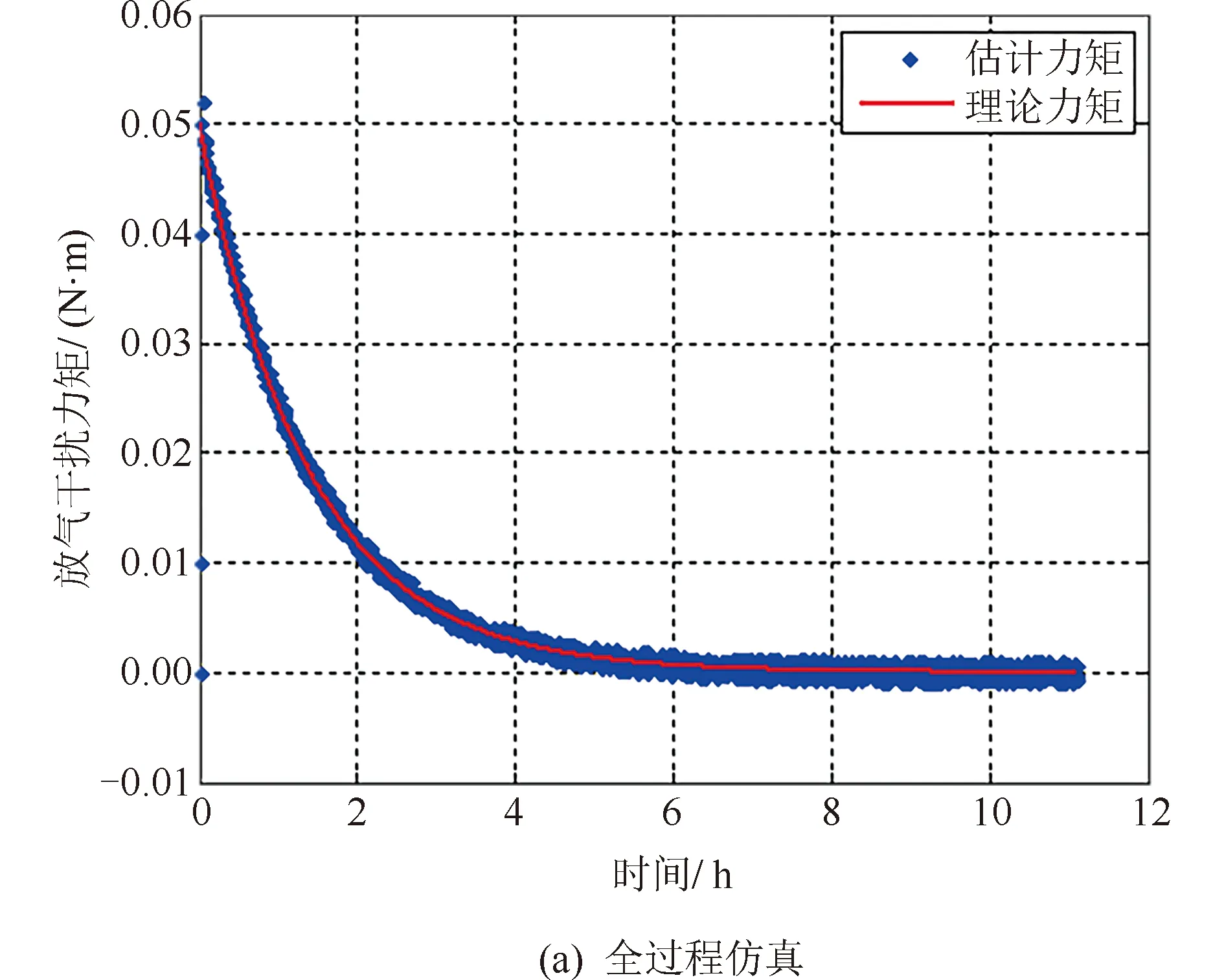
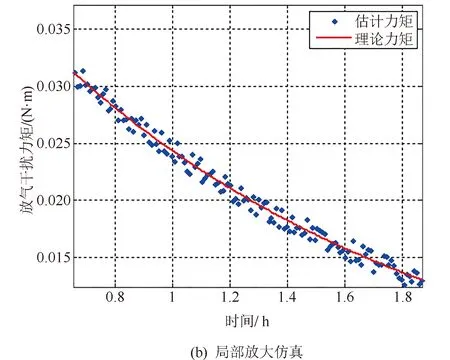
图4 放气干扰力矩估计仿真Fig.4 Simulation result of disturbance torque

由图4可知，太阳翼放气干扰力矩按照负指数函数衰减，估计值与理论值误差小于10%。仿真结果表明：本文算法能够很好实现太阳翼放气干扰力矩的实时估计，且太阳光压力矩对太阳翼放气干扰力矩估计基本无影响，在轨估计算法模型中不用考虑。

3.2 在轨实时估计

利用FY-4卫星星箭分离后在转移轨道段的在轨数据，卫星参数按照3.1节选取。运用陀螺1、2、3、4、5的角度增量解算得到2016年12月10日三轴角速度如图5～图10所示(注：对日定向过程中，偏航轴不进行角度控制)。

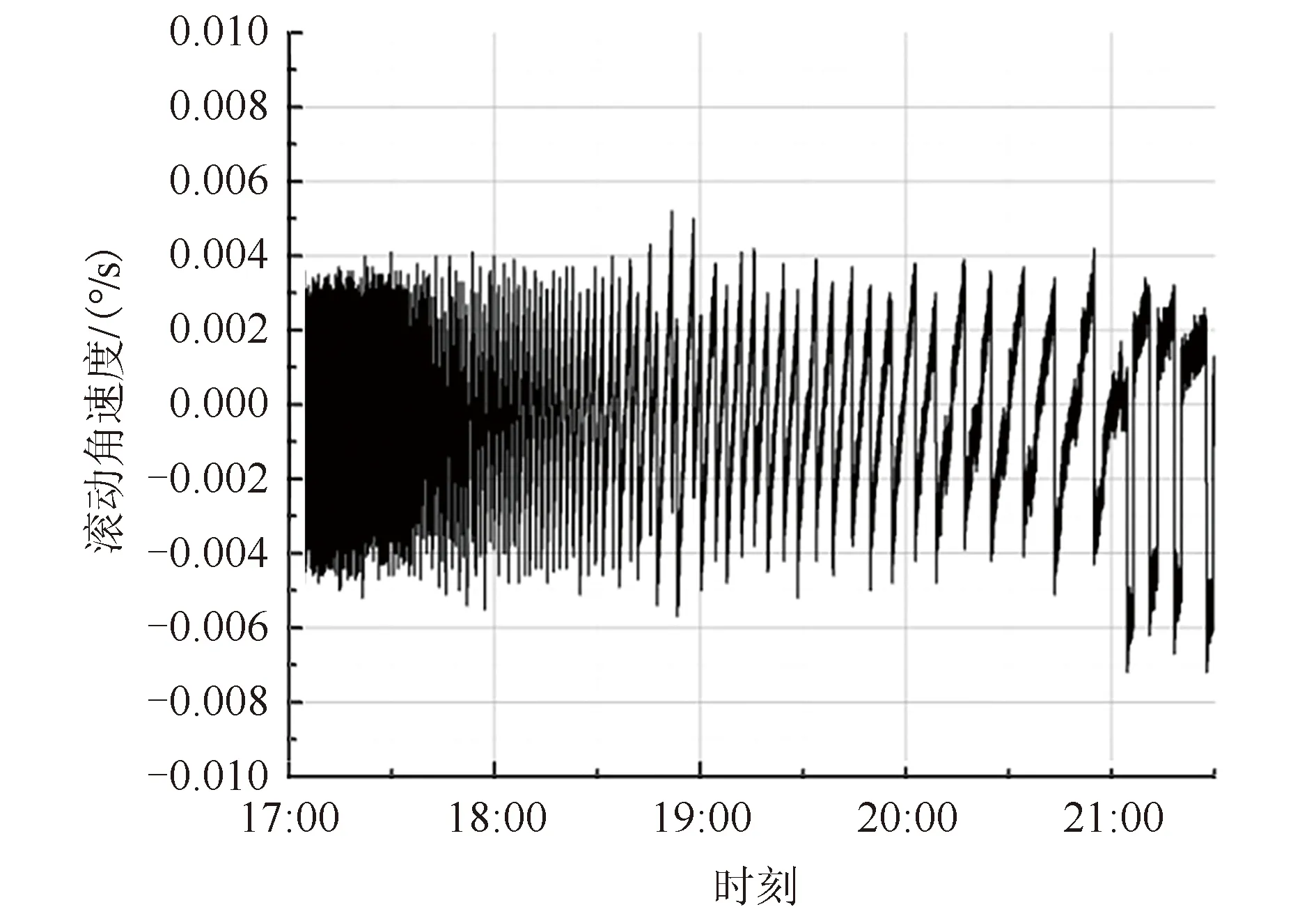
图5 惯性角速度ωx曲线Fig.5 Curve of inertial angular velocity ωx

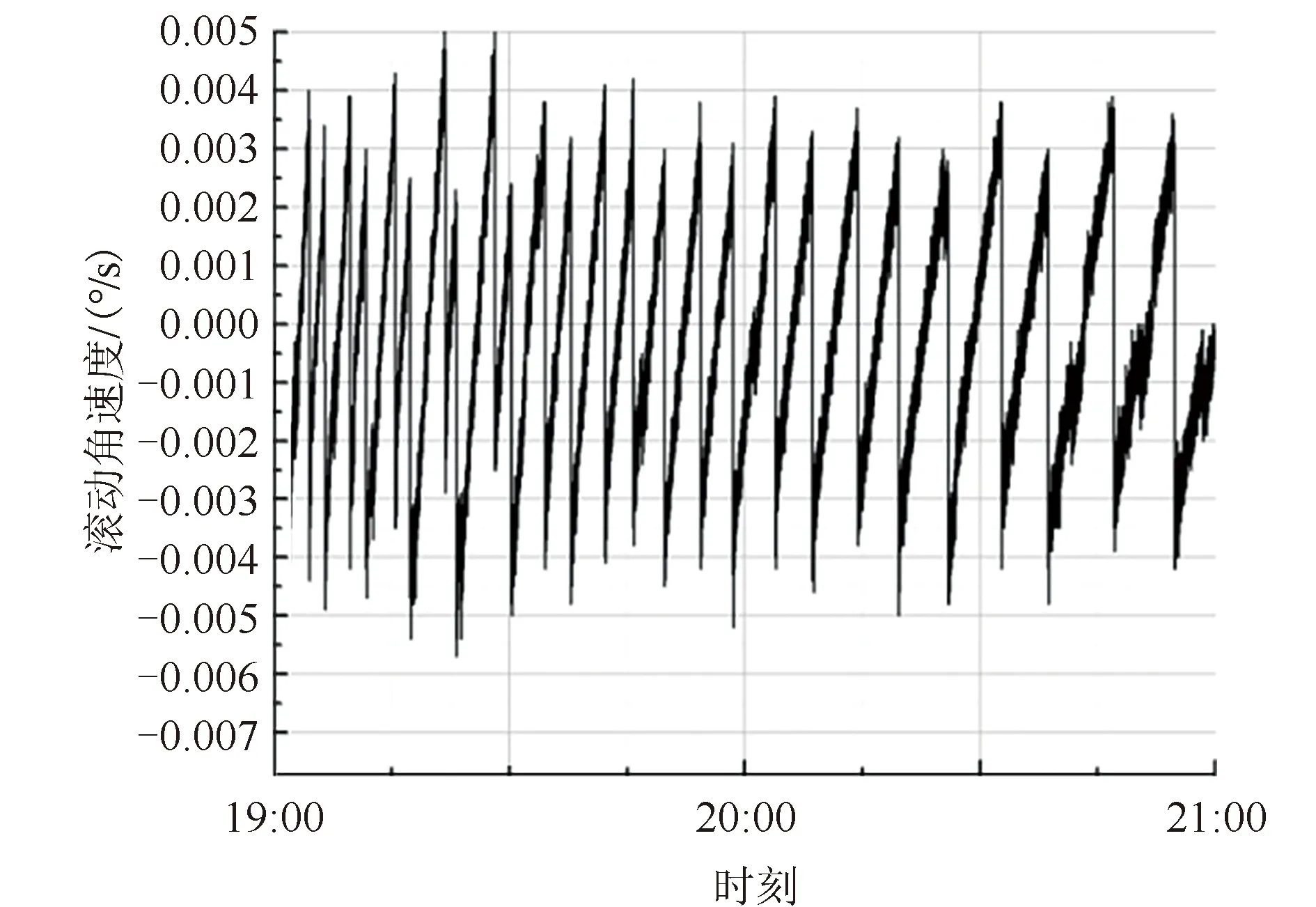
图6 惯性角速度ωx曲线(局部放大图)Fig.6 Curve of inertial angular velocity ωx(amplify curve)

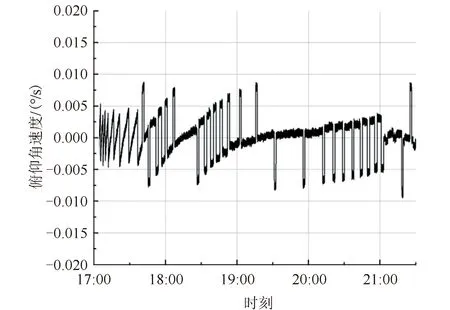
图7 惯性角速度ωy曲线Fig.7 Curve of inertial angular velocity ωy

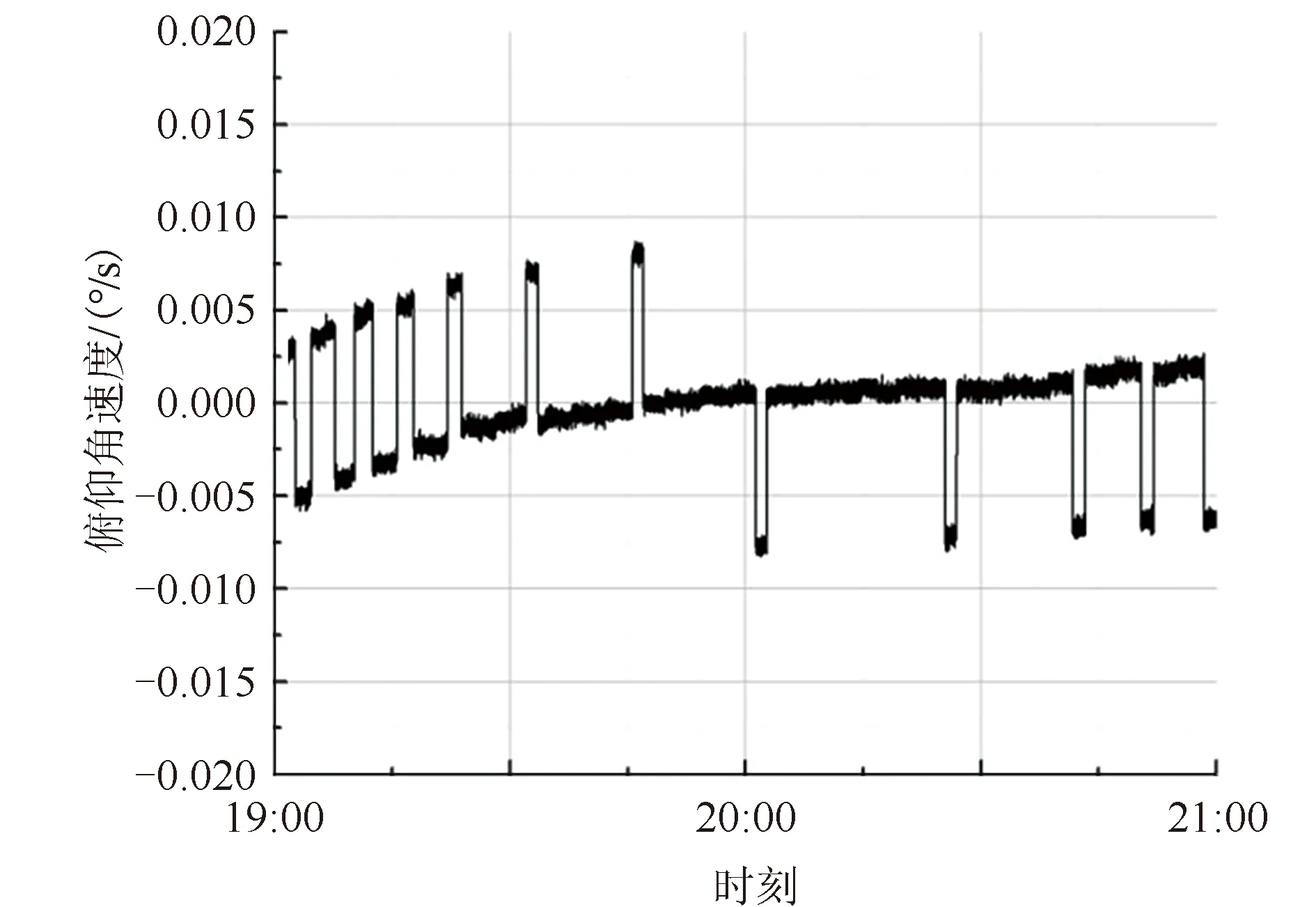
图8 惯性角速度ωy曲线(局部放大图)Fig.8 Curve of inertial angular velocity ωy(amplify curve

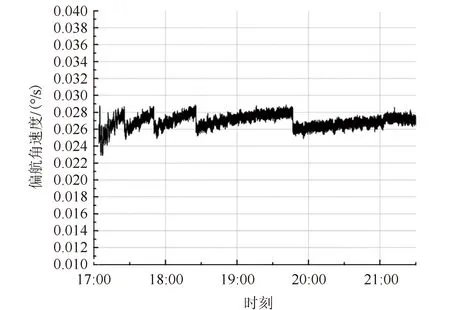
图9 惯性角速度ωz曲线Fig.9 Curve of inertial angular velocity ωz

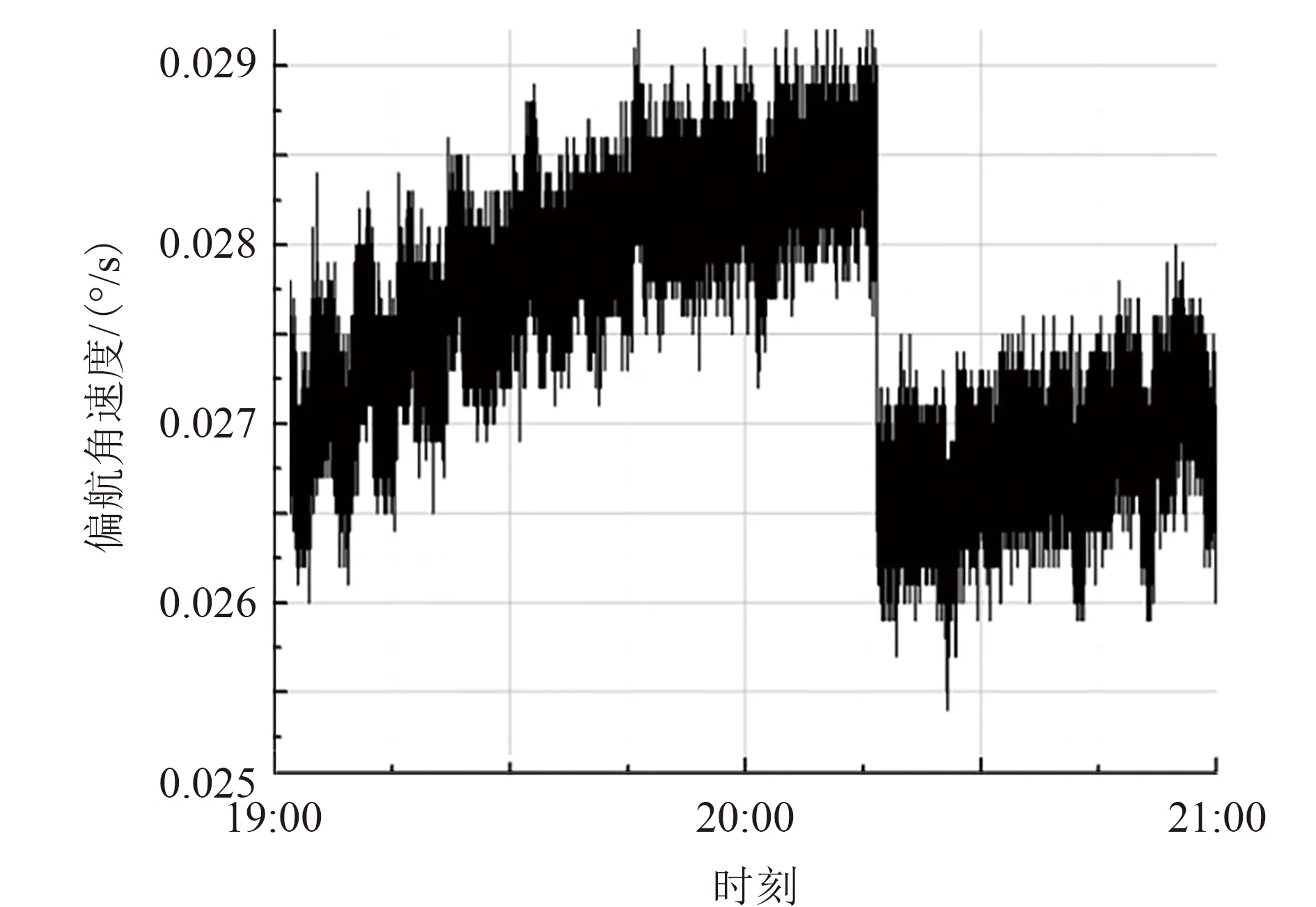
图10 惯性角速度ωz曲线(局部放大图)Fig.10 Curve of inertial angular velocity ωz(amplify curve)

2016年12月10日FY-4卫星太阳翼展开对日定向过程中，太阳翼放气引起的卫星滚动、俯仰姿态角变化曲线如图11所示，Xb轴方向姿态控制推力器工作计时曲线如图12所示。结合图11、图12可知，在卫星对日定向过程中，滚动角曲线呈现单边极限环，说明在Xb轴方向存在一个干扰力矩，即太阳翼放气产生的+Xb轴方向干扰力矩，则卫星推力器产生-Xb轴方向的控制力矩。因此，产生-Xb轴控制力矩的推力器一直工作，计时不断增加，而+Xb轴控制力矩的推力器不工作，推力器计时不变化。

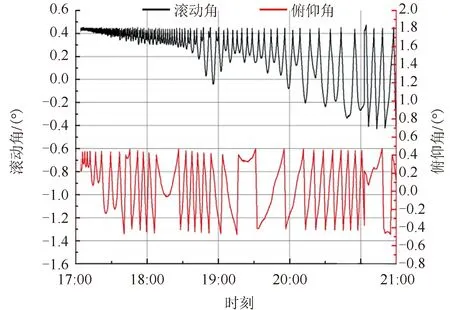
图11 太阳翼放气引起的卫星滚动、俯仰姿态角变化曲线Fig.11 Change curve of attitude angles

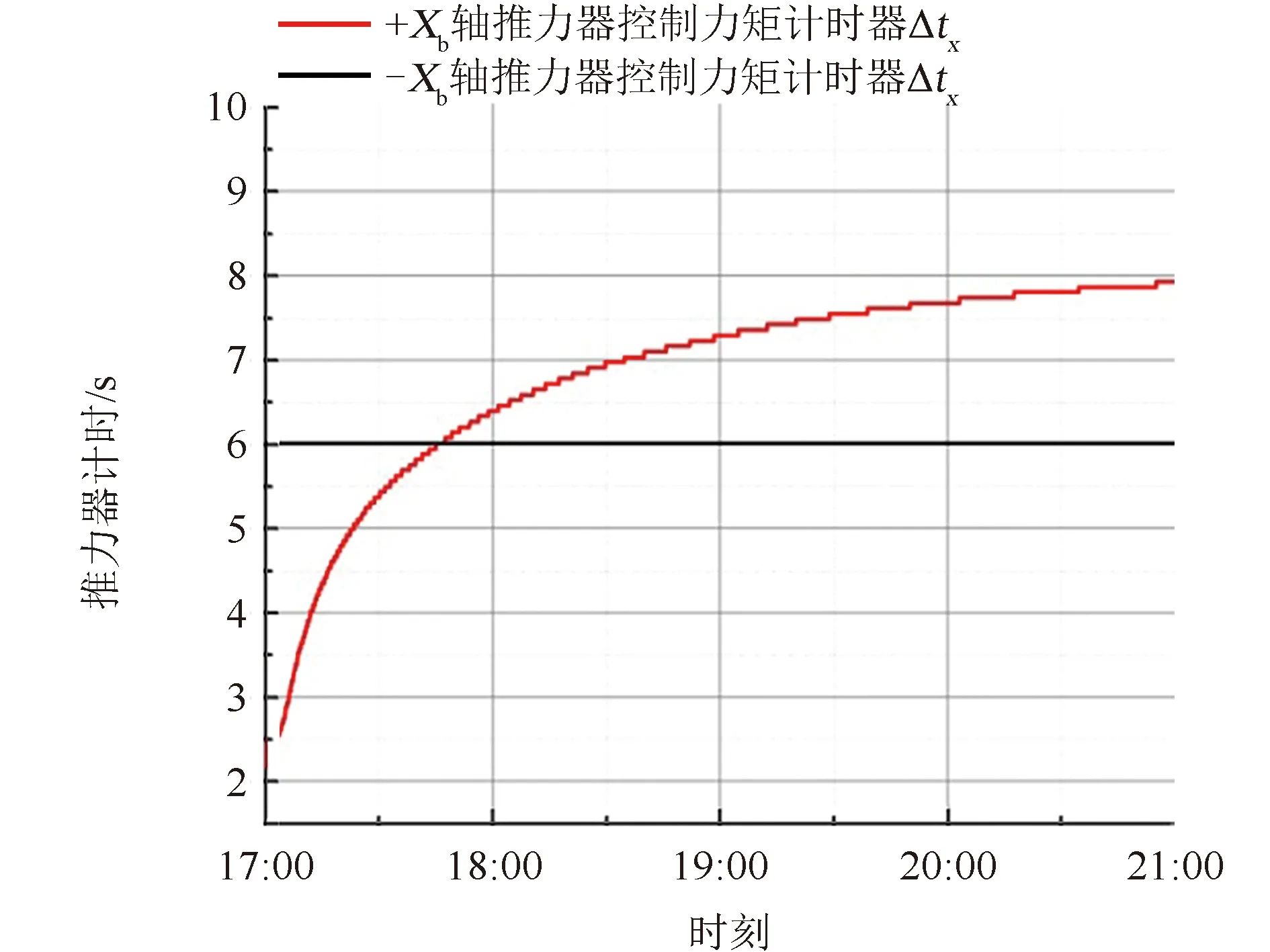
图12 ±Xb轴方向推力器计时曲线Fig.12 Jet timing data of thrusters in ±Xb axis direction

根据上述数据以及本文提出的方法，得到太阳翼放气干扰力矩估计结果如图13所示。

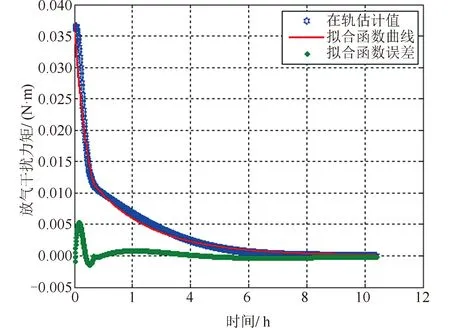
图13 风云四号卫星太阳翼展开后放气干扰力矩估计值、拟合函数及误差Fig.13 Estimation result of disturbance torque caused, fitting function and fitting error of FY-4

将放气干扰力矩按照指数函数进行曲线拟合，得到分段时间函数关系，并与在轨估计值作比较，得到拟合函数的误差值。放气干扰力矩分段时间函数为

(10)

根据在轨实时估计结果，可知：

(1)卫星惯性角速度ωx变化较快，推力器频繁工作进行姿态控制，是因为受到太阳翼放气干扰力矩的影响。在轨放气干扰力矩大小，前0.64 h放气干扰力矩按e-1.8t指数函数衰减，0.64 h后按e-0.485t指数函数衰减。这是因为随着太阳翼蜂窝夹层内气体不断排出，内部压力逐渐变小，气体排出产生的干扰力矩衰减很快。

(2)根据单太阳翼构型可知，放气干扰力矩作用在+Xb轴方向上，根据在轨陀螺数据和推力器工作时间计算太阳翼放气产生的干扰力矩最大达到37 mN·m，比式(1)计算的单太阳翼太阳光压力矩约大2个数量级，并且太阳翼放气时间持续近11 h。

4 结束语

本文根据卫星姿态动力学原理，提出了太阳翼放气干扰力矩估计方法，通过理论仿真，分析了方法的正确性，并运用FY-4卫星在轨实时估计验证了放气干扰力矩按照负指数模型衰减。该方法面向工程实际，不需要建立复杂的复合材料放气模型，即可精确建立单太阳翼卫星姿态动力学特性。

卫星在轨运行受到太阳光压力矩、重力梯度力矩和气动力矩等干扰，且多具有周期性，能够精确建模，可采取前馈控制或反馈控制对干扰进行吸收；而卫星转移轨道段太阳翼放气干扰力矩对姿态扰动较大，估计太阳翼放气干扰力矩对卫星稳态控制有重要意义。

(1)利用估计值及时修正控制参数，避免姿态频繁振荡，减少推力器频繁工作消耗过多燃料。

(2)可作为后续卫星姿轨控设计参考，考虑放气干扰力矩影响，提高系统可靠性和安全性。

(3)在太阳翼制造过程中，适当增加或加大放气孔，使在主动段或转移轨道段初期放气尽快结束，以减少对姿态的影响。

References)

[1] 王献忠,刘赟,张丽敏,等.星载计算机及关键流程可靠性设计[C]//第四届中国指挥控制大会论文集.北京: 中国指挥与控制学会,2016:492-496

Wang Xianzhong,Liu Yun,Zhang Limin,et al.Reliable design for on-board computer and key process[C]//The Fourth Conductor in China Control the General Assembly Talk About Collection of Essays.Beijing:The Fourth Conductor in China Control the General Assembly Talk About Collection of Essays.2016:492-496 (in Chinese)

[2] J W Kim,J L Crassidis,S R Vadali,et al.ISS leak localization using attitude response[J]. AIAA Guidance, Navigation, and Control Conference and Exhibit. Washington D.C.:AIAA,2001

[3] 李海军,黄显林,胡海东,等.基于滤波算法和飞船姿态响应寻找漏气小孔[C]//第25届中国控制会议论文集(上册).哈尔滨:哈尔滨工业大学,2006:492-496

Li Haijun, Huang Xianlin, Hu Haidong, et al. Spaceship leak localization based on the attitude response and filtering algorithm[C]//The 25th Chinese Control Conference(up).Harbin:Harbin Institute of Technology,2006:492-496 (in Chinese)

[4] 雷静,刘莹莹,周凤岐,等.卫星在轨周期干扰力矩辨识与补偿方法的研究[J].西安:西北工业大学学报,2009,27(3):396-400

Lei Jing,Liu Yingying,Zhou Fengqi,et al.A new method for identification of and compensation for periodically disturbing torques of on-orbit satellite[J].Xi’an:Journal of Northwestern Polytechnical University,2009,27(3):396-400 (in Chinese)

[5] 梁彤,张奕群.一种空间飞行器轨控发动机干扰力矩的测试方法[J].现代防御技术,2008,36(1):62-65

Liang Tong,Zhang Yiqun.Method of testing disturbing torque of divert thrusters for the spacecraft[J].Modern Defence Technology,2008,36(1):62-65 (in Chinese)

[6] 杨春光,肖尤明,陈楠,等.真空下非金属材料放气模型与研究综述[J].真空,2016,12(3):48-53

Yang Chunguang,Xiao Youming,Chen Nan,et al.A comprehensive survey of development of outgassing model for nonmetal materials in vacuum[J].Vacuum,2016,12(3):48-53 (in Chinese)

[7] 罗艳,王魁波,张罗莎.聚合物的放气分率与放气模型研究[J].真空科学与技术学报.2015,9(9):1100-1115

Luo Yan,Wang Kuibo,Zhang Luosha.Modelling and characterization of polymer outgassing behavior[J].Chinese Journal of Vacuum Science and Technology,2015,9(9):1100-1115 (in Chinese)

[8] 张亚平,朱颖峰,刘湘云,等.基于扩散放气模型的杜瓦真空寿命分析[J].真空科学与技术学报,2014,34(1):28-31

Zhang Yaping,Zhu Yingfeng,Liu Xiangyun,et al.Influence of diffusion out-gassing on life-time of dewar vessels[J].Chinese Journal of Vacuum Science and Technology,2014,34(1):28-31 (in Chinese)

[9] Schindler N，Schleurner D，Chr Edelmann．Measurement of partial outgassing Rates[J]．Vacuum，1996，47(4):351-355

[10] 陈涛,李玉忠,许忠旭,等.真空热试验中材料放气的放气量及其导热问题[J].航天器环境工程,2006,2(23):103-106

Chen Tao,Li Yuzhong,Xu Zhongxu et al.Material outgassing amount and thermal conduction in vacuum thermal test[J].Spacecraft Environment Engineering,2006,2(23):103-106 (in Chinese)

[11] 袁家军.卫星结构与设计(下)[M].北京:宇航出版社,2004:216-218

Yuan Jiajun.Satellite structure and design(next)[M].Beijing:Astronautics Press,2004:216-218 (in Chinese)

[12] 刘善武,万松,容建刚.航天器空间环境干扰力矩分析与仿真研究[J].航天控制,2015,2(33):78-90

Liu Shanwu,Wan Song,Rong Jiangang.The analysis and simulation of aircraft space environment disturbance torque[J].Aerospace Control,2015,2(33):78-90 (in Chinese)

[13] 徐小方,张华.飞行器转动惯量测量方法研究[J].科学技术与工程,2009,3(6):1653-1660

Xu Xiaofang,Zhang Hua.Method of testing the aerocraft’s moment of inertia[J].Science Technology and Engineering,2009,3(6):1653-1660 (in Chinese)