基于二叉树的太阳系小天体数值历表建立方法∗

胡寿村季江徽

(1中国科学院紫金山天文台南京210008)

(2中国科学院行星科学重点实验室南京210008)

(3中国科学院大学北京100049)

1 引言

小天体探测是21世纪全球深空探测的热点,欧美日目前都已经对部分小天体(包括小行星、彗星和矮行星)展开过实质性的探测活动,嫦娥二号也在2012年12月13日近距离飞越了4179 Toutatis小行星并取得重要的科学成果[1–3].目前新的小天体探测计划(日本的Hayabusa-2、美国的OSIRIS-REx任务)也在开展当中,并且在2022年美国还将发射两次小行星探测任务Lucy和Psyche,分别去探测6颗木星特洛伊小行星以及金属型主带小行星16 Psyche[4−5].

在小天体精确任务轨道设计中,需要计算小天体在完整力模型积分下的轨道.此时从效率和精度考虑,可以对事先积分好的轨道做拟合或插值来获得高精度的光滑连续轨道,以计算任意时刻目标天体的坐标.常用方法包括拉格朗日插值、Neville插值、切比雪夫多项式拟合、样条插值等[6−7],其中切比雪夫多项式因具有较高的数值稳定性而被广泛应用于构建自然天体和人造卫星的数值历表[8−9].

目前已有多篇文献介绍了切比雪夫多项式用于构建大行星/月球和人造卫星(如GPS卫星)数值历表的方法[10–12],其核心思想是将轨道做等区间分段后用一定阶数的切比雪夫多项式进行分段拟合,并将每一段拟合的切比雪夫多项式系数保存下来.在调用历表时,只需根据时间搜寻到对应的系数段后即可反演出该时刻天体的轨道.然而与大行星/月球以及大部分人造卫星不同,许多小天体的轨道偏心率较大,且存在近距离飞越大行星的可能,使得轨道随时间的变化并不均匀.图1给出了目前15630颗近地小行星和924颗彗星轨道偏心率的分布,分别有超过62.2%的近地小行星和超过81.7%的彗星轨道偏心率大于0.4[13]1.图2给出了99942 Apophis近地小行星2000–2050年的轨道图,其中左图为日心平黄道系下Apophis的轨道,右图为Apophis的地心距随时间的变化.可以看到,虽然该小行星偏心率较小,但由于2029年4月13日Apophis将以31600 km的轨道高度近距离飞越地球,导致在此时间前后的轨道发生了较大变化[14−15].对于这部分小天体,它们不宜用传统的等区间分段的方法做拟合或插值,否则容易造成较大的历表误差范围.因此合理的方案是在保持拟合阶数不变的前提下在轨道变化较剧烈的位置处用更小的区间做拟合或插值.但这样带来的问题是如果区间分段不按照一定的规则,那么根据时间计算星历时难以查找到其在历表文件中所处的位置,因此需要一种新的数据结构来组织区间分段信息以提高查找效率.

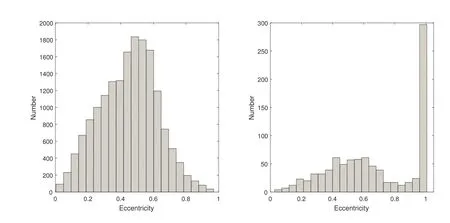
图1 近地小行星(左)和彗星(右)的偏心率分布(数据来源于国际小行星中心1http://www.minorplanetcenter.net/iau/Ephemerides/EphemOrbEls.html)Fig.1 Eccentricity distribution for near-Earth asteroids(left)and comets(right)(data from IAU Minor Planet Center1)

本文引入计算机科学中的二叉树结构来表示不均匀分段的区间,在误差较大处按照二分法对区间分段,直到满足给定精度约束,然后调用星历时在给定时刻可根据二分法查找来定位其系数段的位置.该工作可作为建立大量太阳系小天体数值历表的统一方法,相比于传统等时区间分段方法能够有效压缩数值历表的存储量,可应用于大量目标小天体的精确轨道设计中.

本文安排如下:首先,第2节介绍切比雪夫多项式拟合用于构建大行星/月球数值历表的基本方法;然后,第3节介绍二叉树结构的概念以及我们将其应用于构建小天体数值历表的具体方法;第4节将通过对3颗大偏心率小天体和99942 Apophis小行星做数值历表仿真来说明本文介绍的方法在小天体中的应用.

图2 99942 Apophis小行星2000—2050年的轨道(左)及地心距(右)Fig.2 The orbit(left panel)and geocentric distance(right panel)of 99942 Apophis from 2000 to 2050

2 建立数值历表的基本方法

2.1 切比雪夫多项式

在数学上,Chebyshev多项式是以递推方式定义的一系列多项式,计算效率很高,且具有良好的数值稳定性[16−17].第1类Chebyshev多项式递推公式如下:

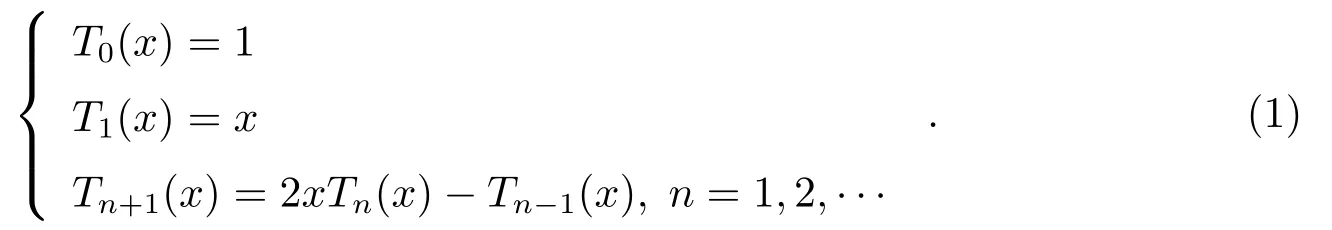
第2类Chebyshev多项式递推公式为:

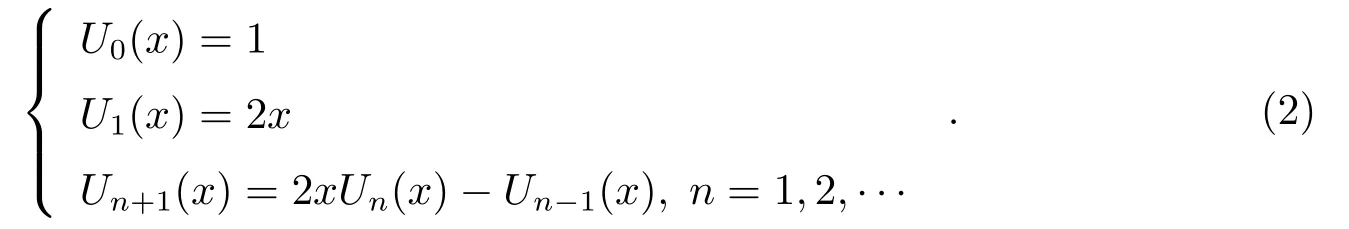
以上(1)–(3)式中x的范围均为−1≤x≤1.切比雪夫多项式具体应用于数值历表构建的基本方法在文献[10]中有较为详细的叙述,这里只做简略介绍.

假设拟合阶数为D,记X和V分别为位置和速度矢量中的任一分量(采用位置和速度作为轨道参数),ck为对应的切比雪夫多项式系数,则X和V的计算公式为:

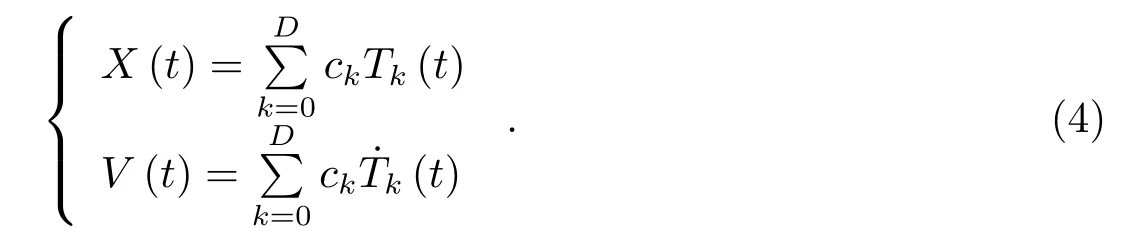
(4)式中需要将实际的时间引数(儒略日JD)转换到归一化时间范围[−1,1],即:

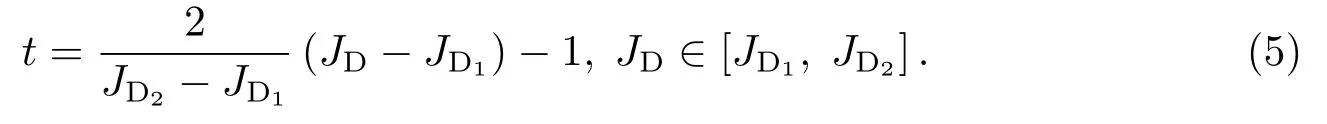
这样,接下来的任务只需求出系数ck.

2.2 切比雪夫多项式系数计算

采用类似建立JPL(喷气推进实验室)历表的方法,在各分段内按均匀归一化的时间步长1/4从1到−1(即1,3/4,1/2,1/4,···,−3/4,−1)进行采样. 这样总共有18个采样点(9个位置和9个速度),切比雪夫多项式系数满足如下条件:

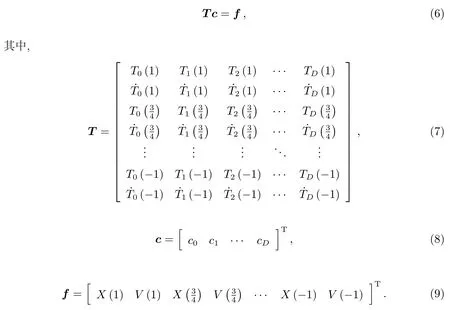
T是一个18×(D+1)的矩阵,因此阶数最高不能超过17,如果D＜17,则(6)式是一个超定方程组,可以用最小二乘法来求解.但为了使得最后生成的历表随时间连续,则需要保证在区间两端连续,因此在(6)式的基础上还需要增加以下4个约束条件:

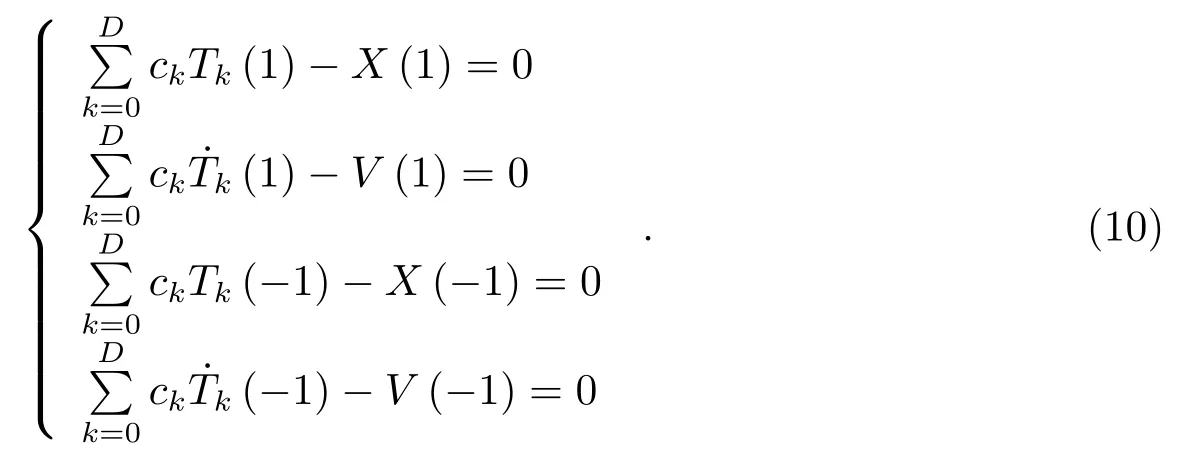
采用拉格朗日乘子法可以求解(6)式和(10)式.忽略过程,整理后得:

W为18×18的权重矩阵(对角矩阵).各对角元素分别对应各采样点的位置或速度权重(奇数点对应位置,偶数点对应速度),一般取位置权重为1,并可通过增加或减小速度权重值来减小或提高速度拟合精度.在文献[10]中建议的取值为:

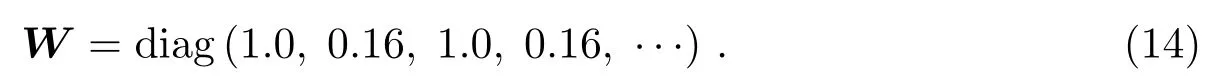
本文算例中W的取值与之相同.从(14)式中求出c即得到该分段内的切比雪夫多项式系数(l可舍弃).

2.3 数值历表构建和读取流程

对于大行星/月球和大部分人造地球卫星,由于轨道偏心率不大,轨道变化均匀,传统的方法就是直接对轨道做等区间分段(JPL大行星/月球历表,GPS卫星星历表等都用这种方法),生成历表文件的主要流程如下:

(1)获得原始轨道数据,给定拟合阶数和区间长度;

(2)对整条轨道做等区间分段;

(3)对各区间做切比雪夫多项式拟合,并保存获得的系数到历表文件;

(4)保存阶数、区间分段等信息到历表文件头.根据历表文件计算t时刻轨道的流程如下:

(1)载入历表文件到内存中;

(2)根据时刻t和历表文件头信息查找到对应系数段;

(3)根据系数反演计算t时刻的轨道.

以上方法应用于轨道随时间均匀变化的小天体也是合适的,但是正如前文所说,有相当一部分小天体的轨道变化可能是较不均匀的,这导致等区间分段得到的拟合精度变化范围较大.若在误差较大处缩小分段区间,但如果没有给定一定的规则,则调用历表时不易根据时间反查到对应的系数段位置.因此本文考虑采用二分法来对区间做分段,采用二叉树结构来存储分段信息,这样在给定时刻后可以用快速的二分法查找来定位系数位置,下一节将详细介绍这种方法.

3 二叉树结构在数值历表中的应用

在计算机科学中,二叉树是一种每个结点至多有两个分支的树结构.树中每一个数据元素称为结点,如果该结点包含有子结点,则称之为分支结点,否则称为叶子结点.本文考虑一种特殊的二叉树结构,该二叉树的结点要么是叶子结点,要么是含有两个子结点的分支结点(根据国外文献的定义,这种树结构又称为满二叉树).

为了阐述二叉树在建立数值历表中的应用,图3给出了一段轨道做分割后表示成二叉树结构的示意图.

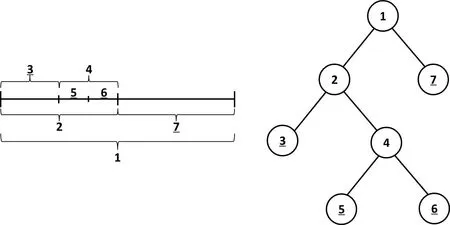
图3 轨道段作不规则二分法分段后(左图)用二叉树结构表示(右图),带下划线的为叶子结点Fig.3 An orbit section is divided into irregular pieces(left panel)by dichotomy,and represented with binary tree(right panel),the underline symbol means leaf node

图3中,各数字为轨道区间的编号,其中带下划线的为不再继续分段的轨道段(即叶子结点).以图3为例,结合二叉树结构建立数值历表的步骤可叙述如下:

(1)获得原始轨道数据,给定拟合阶数和历表拟合精度p;

(2)评估1的拟合误差,由于误差大于p,将1等分成2和7,记录此次分段信息;

(3)评估2的拟合误差,由于误差大于p,继续将2分割成3和4,记录此次分段信息;

(4)评估3的拟合误差,由于误差小于p,保存拟合得到的系数;

(5)评估4的拟合误差,由于误差大于p,继续将4分割成5和6,记录此次分段信息;

(6)评估5的拟合误差,由于误差小于p,保存拟合得到的系数;

(7)评估6的拟合误差,由于误差小于p,保存拟合得到的系数;

(8)评估7的拟合误差,由于误差小于p,保存拟合得到的系数;

(9)保存整个轨道段的区间分段信息并建立区间与系数段索引的关系;

(10)保存阶数、区间分段等信息到历表文件头,结束.

要计算某时刻t的星历,此时可以利用二分法查找,例如假设t在6区间内,则程序将按照以下步骤查找(忽略其他步骤):

(1)发现t在区间1内,因为1为分支节点,继续查找;

(2)继续判断,发现t在2内,因为2为分支节点,继续查找;

(3)继续判断,发现t在4内,因为4为分支节点,继续查找;

(4)继续判断,发现t在6内,因为6为叶子节点,可根据叶子节点保存的系数段索引提取相应的切比雪夫多项式系数,结束查找.

以上根据t查找系数段索引的次数最多为二叉树的深度,由于查找运算只是简单的判断程序,耗费的计算机时间可忽略.查找结束后,即可根据提取到的切比雪夫多项式系数计算天体在该时刻的位置和速度.从以上叙述可以知道,我们的方法(下称为新方法)与传统方法的区别在于生成历表时增加了一个区间分段的操作,而读取历表时增加了一个根据时间反查系数段位置的操作.最终生成的历表文件不仅包含文件头信息和切比雪夫多项式系数,还要保存分段信息(但分段信息占用的存储量非常小),相比于传统方法复杂了一些,但流程是清晰的.

若记分段数为P,则可以计算最终生成的历表存储的系数个数N为

通过下文的数值仿真可以看到,由于通过新方法减小了N的值,使得对于部分小天体可以大大减小历表文件的大小,这对需要生成大量小天体数值历表的情况(例如需要对大量候选目标小行星计算发射窗口)是很重要的.

4 数值仿真

考 虑3颗 近 地 小 行 星4179 Toutatis、 3200 Phaethon、 99942 Apophis和 彗 星2P/Encke(其中,Toutatis、Phaethon和Encke均为大偏心率小天体,而Apophis将于2029年4月13日近距离飞越地球),其各自的轨道信息见表1的第2到4行.这里将采用本文介绍的新方法建立各自的数值历表,取历表的时间跨度为5 yr(2027–2032年),容许的最大位置误差为1 km,拟合阶数为10,生成的数值历表信息如表1所示,其中第5行为区间分段的范围,第6行为总的区间数.可以看到:对于偏心率越大的天体,区间的变化范围越大,而Apophis飞越地球导致的轨道变化使得最小区间只有0.11 d.图4以Phaethon和Apophis为例演示了区间分段对应的轨道位置,显然Phaethon的分段较密处发生在近日点前后,而Apophis发生在飞越地球前后.

这里与传统方法生成的历表做一比较,分别取4颗小天体的总分段数为表1中第6行的值(即分别取为20、53、44和32),采用均匀区间分段,生成的数值历表的位置、速度误差与新方法的对比如图5所示.图5的结果表明:对于3颗大偏心率小天体Toutatis、Phaethon和Encke,传统方法的拟合误差在近日点附近迅速放大,远日点和近日点的位置误差分别可以相差2个、8个和6个量级,而Apophis由于在飞越地球后轨道有较大的改变,导致位置误差变化范围也可以达到8个量级.因此,传统的等区间分段法确实不适用于建立这些小天体的数值历表,否则为了达到1 km精度,根据表1第5行的结果,它们分别需要取相等的分段区间为28.5 d、1.8 d、0.11 d和7.1 d.相比于新方法,这会导致系数的存储量迅速增大.表1第7行给出了在相同的1 km位置精度下,新方法相对于传统方法所节省的存储空间,显然偏心率越大的小天体节省的空间越可观,而Apophis的轨道特性甚至可以导致节省99.7%的存储量.

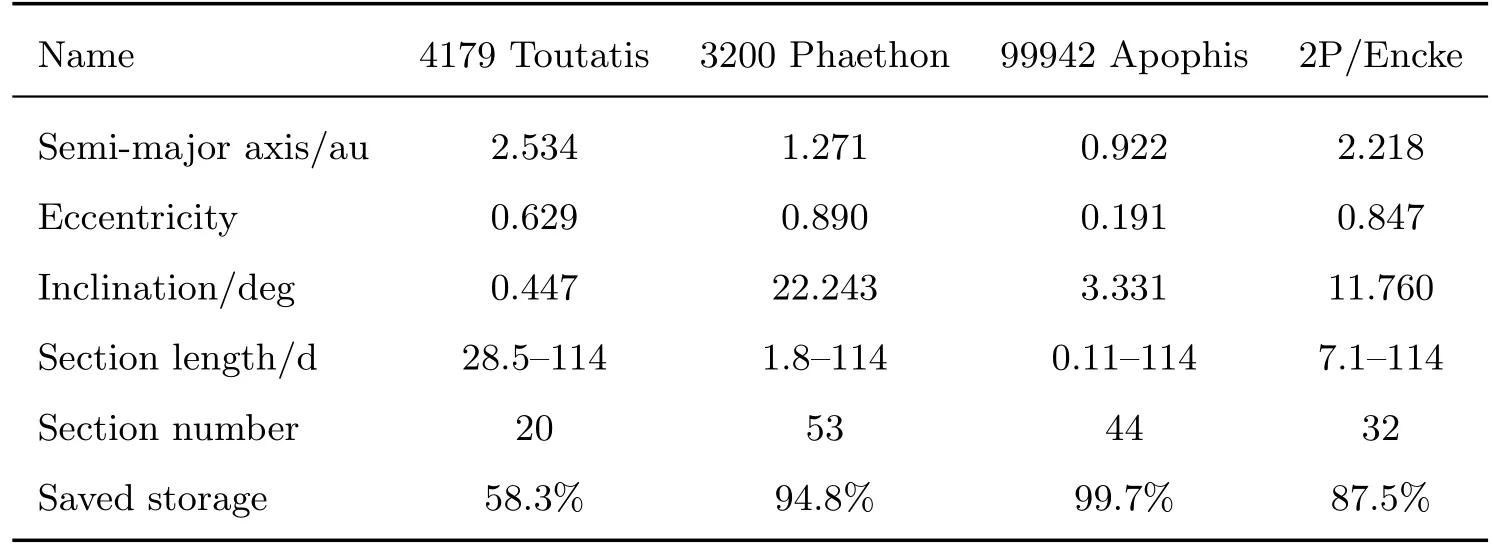
表1 4颗小天体轨道生成的数值历表信息Table 1 The information of numerical ephemerides for the four minor bodies

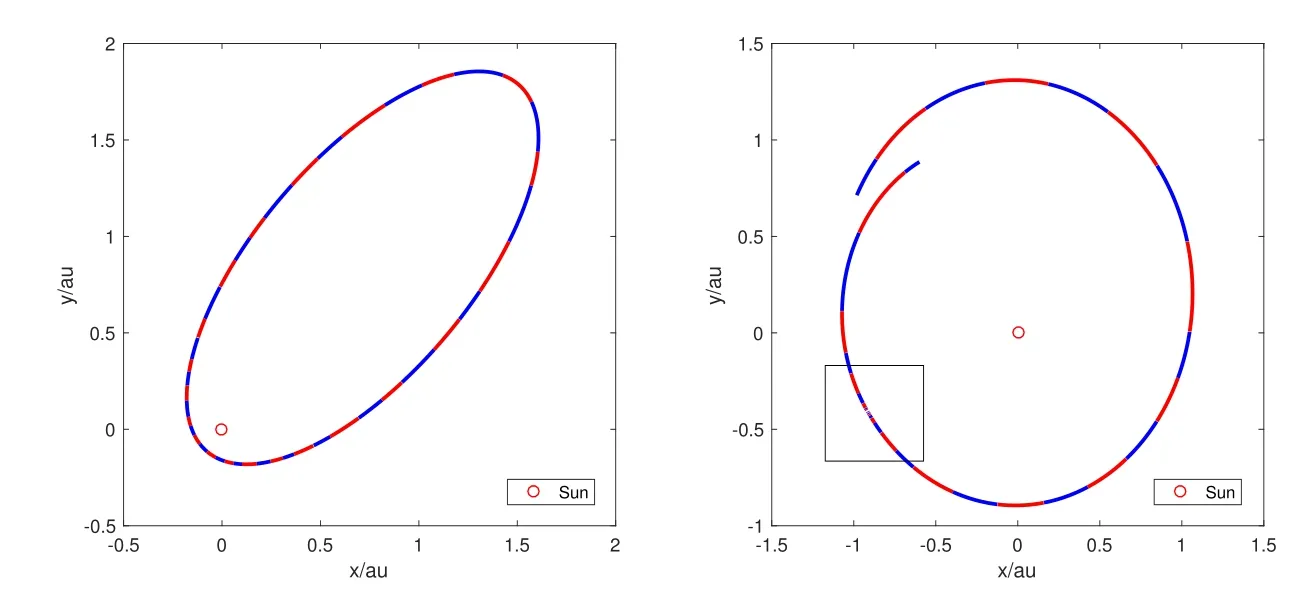
图4 左图为3200 Phaethon小行星在一个轨道周期内的轨道分段,右图为99942 Apophis在2029年1月—2030年3月的轨道分段,其中方框内为Apophis飞越地球前后30 d的轨道段,图中以红色和蓝色来区分相邻分段.Fig.4 The demonstration of orbit division for 3200 Phaethon in one orbit period(left panel)and 99942 Apophis from 2029 Jan.to 2030 Mar.(right panel).The square frame in the right panel contains Apophis orbit in 30 d before and after the Earth- flyby.The red and blue colors are used to distinguish the adjoining sections.

对以上4颗小天体,若取不同的拟合阶数D(D∈[6,16]),各自的分段数P和系数个数N随D的变化如图6所示.显然随着D的增大,P值逐渐减小,但对于不同的天体,最小N值对应的D值也不同.为了最大程度减小系数个数,对不同天体应取不同的拟合阶数D.从图6结果来看,D从10到13取值并无显著差异,但从计算效率角度考虑,D取值一般不应过大.文献[10]也给出了JPL历表中各大行星和月球拟合采用的阶数,可供参考.

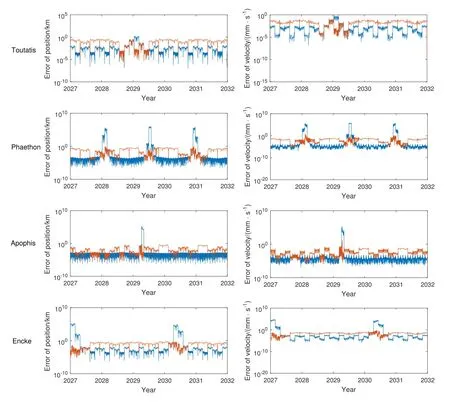
图5 传统方法(蓝色)与新方法(橙色)生成的历表的位置和速度误差的对比Fig.5 The comparison of position and velocity errors of ephemerides for old method(blue)and new method(orange)

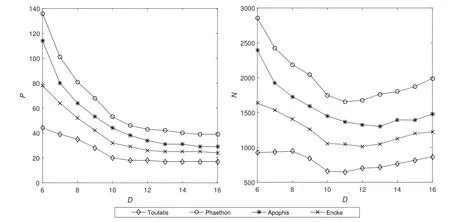
图6 对这4颗小天体,取1 km的最大允许位置误差,分段数P和系数个数N随拟合阶数D的变化.Fig.6 For the four minor bodies,assuming the allowable position error is 1 km,the figure shows the variation of section number P and coefficient number N with fitting order D.

5 总结

本文基于二叉树结构提出了一种通用的小天体数值历表构建方法.该方法继承了传统的分段轨道切比雪夫多项式拟合方案,但将传统的等区间分段修改为非等区间分段,即依据区间内的实际拟合精度来调整分段区间,使得最终所有区间内的精度都满足给定要求.该方法采用二分法做区间分段,最后采用二叉树结构来组织所有的区间分段信息,这样在根据时间来反查对应的切比雪夫多项式系数时能够采用快速的二分法搜索进行查找,具有较高的查找效率,解决了非等区间分段下的系数搜索问题.由于该方法能保证只在拟合误差较大的位置(一般为轨道剧烈变化的位置)采用较小的区间分段,而其他位置仍可采用较大的区间,从而能减小历表文件的大小而不影响整个历表的拟合精度.此优点在需要构建大量小天体数值历表时更能够明显体现出来.如果要将多颗小天体的历表合并成一个历表文件,只需在文件头中多增加相应信息,具体步骤不赘述.本文提供的方法尤其适用于构建大偏心率或可能近距离飞越大行星的小天体数值历表.文中以3颗大偏心率小天体4179 Toutatis、3200 Phaethon和2P/Encke以及将近距离飞越地球的99942 Apophis小行星为例,通过数值仿真证实了该方法的有效性.另外,由于该方法没有对天体的轨道性质做任何要求,因此既可作为构建太阳系小天体数值历表的通用方法,甚至也可用于构建大偏心率人造卫星的数值历表.

[1]Huang J C,Ji J H,Ye P J,et al.NatSR,2013,3:3411

[2]Zhao Y H,Ji J H,Huang J C,et al.MNRAS,2015,450:3620

[3]Jiang Y,Ji J H,Huang J C,et al.NatSR,2015,5:16029

[4]Lauretta D S,Team O R.An Overview of the OSIRIS-REx Asteroid Sample Return Mission.43rd Lunar and Planetary Science Conference,Woodlands,March 19–23,2012

[6]魏二虎,柴华.全球定位系统,2006,31:13

[7]赵齐乐,刘经南,葛茂荣,等.武汉大学学报(信息科学版),2006,31:879

[8]陈刘成,贾晓林,莫中秋.天文学进展,2006,24:167

[9]张如伟,刘根友.大地测量与地球动力学,2008,28:115

[10]Newhall X X.Numerical Representation of Planetary Ephemerides.Proceedings of the 109th Colloquium of the International Astronomical Union.Gaithersburg,Maryland,July 27–29,1989:305

[11]Standish E M,Williams J G.Orbital Ephemerides of the Sun,Moon,and Planets//Seidelmann P K.Explanatory Supplement to the Astronomical Almanac.Mill Valley,CA:University Science Books,1992:279

[12]Folkner W M,Williams J G,Boggs D H,et al.The Planetary and Lunar Ephemerides DE430 and DE431.Interplanetary Network Progress Report:IPN Progress Report 42-196.US:California Institute of Technology,2014

[13]Malhotra R,Wang X Y.MNRAS,2016,265:4381

[14]Manca F,Sicoli P,Test A.MmSAI,2016,87:72

[15]Wlodarczyk I.Proceedings of the Polish Astronomical Society,2016,3:108

[16]Rivlin T J.The Chebyshev Polynomials.New York:John Wiley&Sons,1974

[17]林成森.数值计算方法:下册.2版.北京:科学出版社,2005