BDS/GPS星载原子钟的短期钟差预报模型研究∗

布金伟 左小清 常 军 李小龙

(1昆明理工大学国土资源工程学院昆明650093)

(2国家测绘地理信息局第一大地测量队西安710054)

(3东华理工大学测绘工程学院南昌330013)

1 引言

原子钟是卫星导航系统有效荷载的核心部分,其性能直接决定着导航定位和时频传递的精度,高准确度和高稳定度的原子频标和时间系统是确保高精度导航定位的关键[1−2].当前全球4大卫星导航系统中,美国的GPS(Global Positioning System)导航卫星采用了铯原子钟和铷原子钟结合的方式,俄罗斯的GLONASS(Glonass Navigation Satellite System)导航卫星和欧盟Galileo导航卫星均采用铷原子钟和被动型氢原子钟结合的方式,而中国的BDS(BeiDou Navigation Satellite System)系统主要是由4颗MEO(Medium Earth Orbit)、5颗IGSO(Inclined Geosynchronous Satellite Orbit)和5颗GEO(Geostationary Earth Orbit)卫星构成的异构星座,其原子钟均采用铷原子钟[3].由于BDS导航卫星钟是国产铷钟,其精度和稳定性相较于GPS和Galileo稍显逊色,其星载卫星钟性能及预报模型的研究将成为我国导航定位工作的研究热点[4].

卫星钟差的中短期预报对于卫星钟时间同步以及实时精密单点定位(PPP)有重要作用.近年来,国内外学者针对钟差预报工作开展了大量的工作,得到不少重要的结论.如国外学者Breakiron等人考虑了钟差的周期性特点[5−6],提出利用附加周期项的2次多项式拟合模型,6 h的预报精度达到2 ns.Epstein等人针对GPS在轨Rb钟,发现GPS卫星采用卡尔曼滤波进行预报时6 h的预报精度为8–9 ns,并且当预报时间变长时,预报精度随之降低[7].国内学者王国成等人利用径向基函数神经网络对4颗GPS卫星钟差连续进行1 h和1 d的预报[8],分别取得了均方误差优于0.6 ns和1 ns的预报精度.程瑞江等人引入了GM(Gray Model)-LSSVM(Least Square Support Vector Machines)钟差预报模型,采用全局寻优能力较强的遗传算法对模型的参数选取过程进行优化,优化后的模型预报精度小于1.3 ns[9].目前,钟差预报的现状是卫星钟差模型多元化,但不具有较强的普遍适应性,预报模型与卫星钟自身物理特性的结合不充分[10].因此,考虑到计算效率和计算精度,结合各模型的优势,探索适应能力强、预报精度高的组合模型是未来钟差预报模型的热点方向[11].

从上述研究现状可以看出,目前卫星钟差预报研究大部分集中在GPS导航卫星,且任何一种单一模型都不可能完全适用于各种卫星钟差序列.此外对于我国BDS/GPS卫星钟差预报的研究工作开展得还不够具体和广泛.因此,本文重点对BDS/GPS卫星钟差短期预报模型进行了深入的研究,在介绍4种单一模型(多项式模型(QR)、灰色模型(GM)、时间序列模型(ARMA)和广义回归神经网络模型(GRNN))的基础上,引入了经典权组合模型(CM)和修正经典权组合模型(Modified CM),最终得出了一些有意义的结论.

2 钟差预报模型

2.1 多项式模型(QR)

常用的多项式钟差预报模型主要包括1阶模型、2阶模型以及高阶多项式模型.本文以2次多项式为例,其数学模型为:

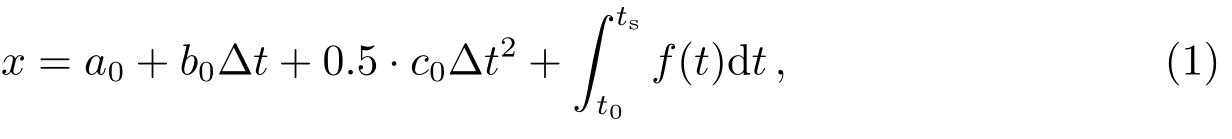
式中,Δt=ts−t0,t0为卫星钟的参考时刻,x为ts时刻的卫星钟差观测值,a0、b0、c0为钟差模型参数,考虑到卫星钟的物理特性,3个参数分别对应的是钟差(相位)、钟速(频率)、钟漂(频漂);是由于频率的随机误差而引起的一种随机钟差.

该模型建模简单,物理意义明确.对于GNSS(Global navigation satellite system)卫星钟差预报而言,1阶模型和2阶模型被分别应用于GPS和GLONASS系统的广播星历实时钟差预报中.考虑到不同原子钟的频率稳定性及频漂特性,一般情况下铯原子钟(Cs)宜采用1次多项式进行拟合预报,铷原子钟(Rb)宜采用2次多项式进行拟合预报[12−13].

2.2 灰色模型(GM)

其中,a、u为模型参数.

在实际计算中,以相邻两值的平均值和相邻两点的差代替微分方程中的x(1)和进行离散化,可得到近似线性方程

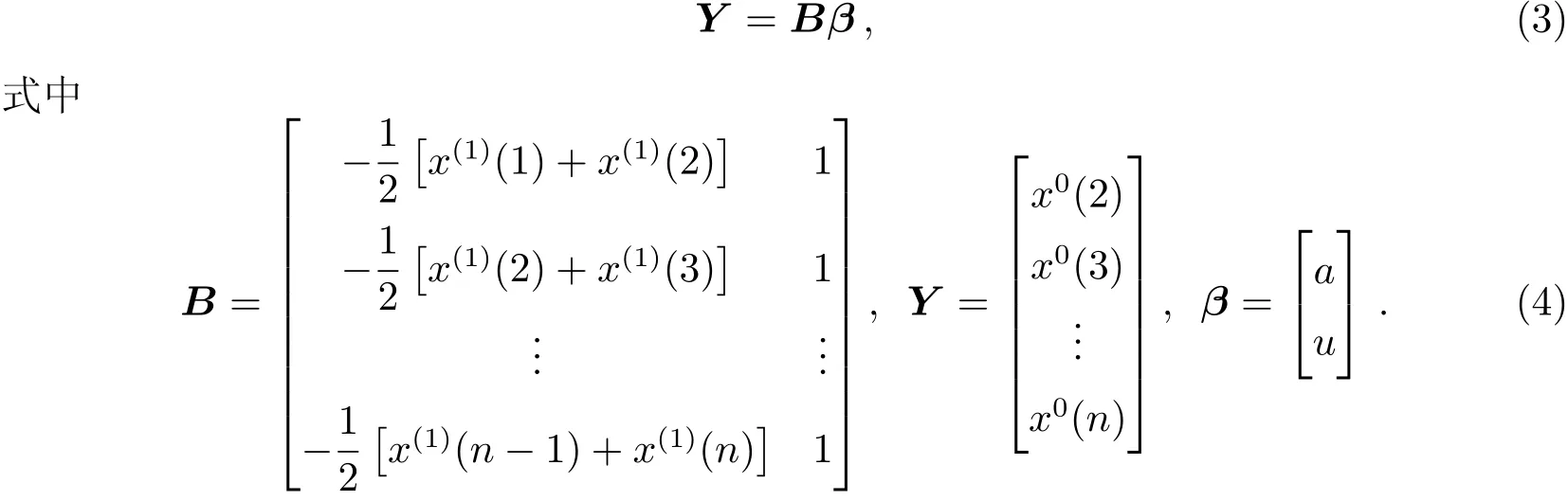
根据最小二乘原理可求得参数β的估值

在顾及初始条件x(1)(1)=x(0)(1)时,微分方程的解为:

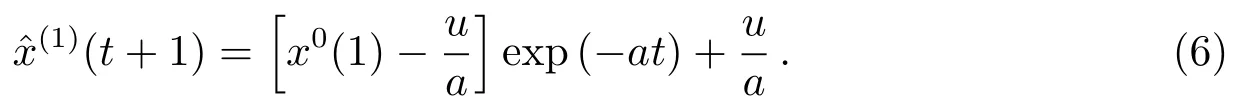
通过累减还原,可得到原始序列

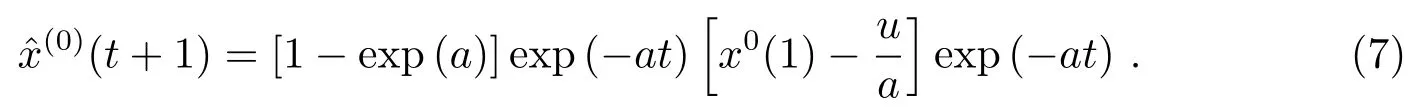
灰色模型只需要少量的已知数据(4个以上的观测值)就可以建立模型进行预报.该方法的优点是减少了建模的数据量并且提高了建模速率,缺点是无法充分利用更多的已有数据来提高其预报精度.

2.3 时间序列模型(ARMA)

ARMA(Autoregressive Integrated Moving Average)模型是组合了自回归模型(Autoregressive,AR)和滑动平均模型(Moving Average,MA)的一种综合预测方法[14−15].ARMA模型的数学表达式为:

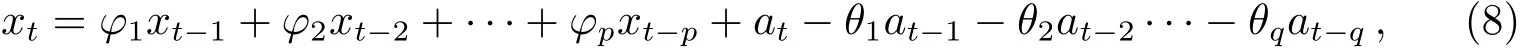
式中,p、q为正整数,分别为该模型的自回归阶次和滑动平均阶次;φ1,φ2,···,φp为模型参数或自回归系数;θ1,θ2,···,θq为模型参数或滑动平均系数;at为白噪声序列;xt为平稳、正态、零均值的时间序列.

2.4 广义回归神经网络模型(GRNN)

广义回归神经网络(Generalized Regression Neural Network,GRNN)结构共有4层组成,分别为输入层、模式层、求和层和输出层[16−17].对应网络输入为X={x1,x2,···,xl}T,其输出为Y={y1,y2,···,yk}T.输入层神经元的数目等于学习样本中输入向量的维数,直接将输入向量传递给模式层.模式层神经元数目为学习样本的数目n,模式层神经元传递函数为:

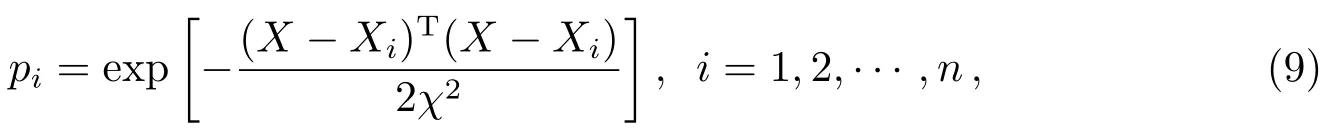
式中,X为网络输入变量,Xi为第i个神经元对应的学习样本,χ为光滑因子.

求和层中使用两种类型神经元求和.一种为对所有模式层神经元的输出进行算术求和,其模式层与各神经元的连接权值为1,传递函数为:

另一类计算公式为对所有模式层的神经元进行加权求和,模式层中第i个神经元与求和层中第j个分子求和神经之间的连接权值为第i个输出样本Yi中的第j个元素,传递函数为:

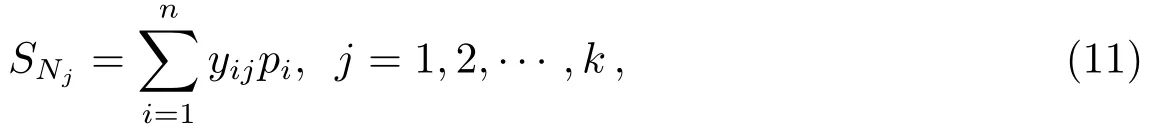
其中,yij为第i个输出样本Yi中的第j个元素.

输出层中的神经元数目等于学习样本中输出向量的维数k,各神经元将求和层的输出相除,神经元j的输出对应估计结果

2.5 组合模型

2.5.1 经典权组合模型

组合模型是采用加权平均值的方法组合多种单一模型得到的预测钟差序列.该方法通过给定不同预测模型一定的权,取加权后的平均值为组合的预报结果,其中权值的确定是关键.假设有i个单一预测模型,则组合模型的数学表达式为[18−20]:

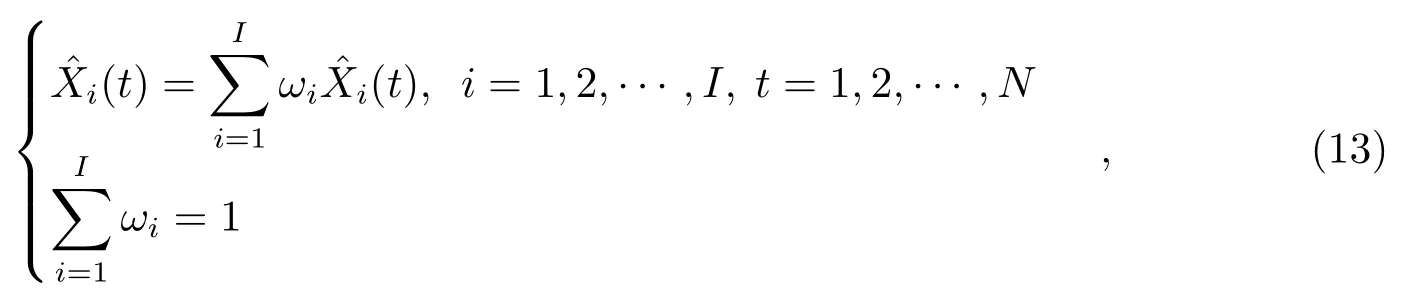
根据定权方法和约束条件的不同,加权平均值法可以分为多种形式,如:经典权、最优权方法等.本文介绍经典权方法,其定权方法如下:

设有一组观测序列X=(x(1),x(2),···,x(n)),通过单一模型得到的拟合值序列为,得到的残差序列为,可以求出残差序列的均方误差.由此经典权方法的定权公式可表述为:

2.5.2 修正经典权组合预报模型

在进行钟差的拟合和预报过程中,可以发现有些建模方法的拟合精度很高,但其预报精度却不一定好.因此在进行多时段连续预报时,可以考虑用各模型历史时段的预报精度来修正当前的组合权值,改善仅仅依靠拟合精度定权的不可靠性.其修正原理如下:选取i个单一预报模型分别进行连续多时段预报,并将其预报结果进行线性组合.在进行第i时段的预报时,可以获得单一模型的前i−1个时段的预报误差序列,由此可以建立学习权.第i个模型在第i−1个时段的预报误差序列为εi(i−1),其对应的均方误差.对于单一模型在第i时段的学习权可定义为[18−20]:

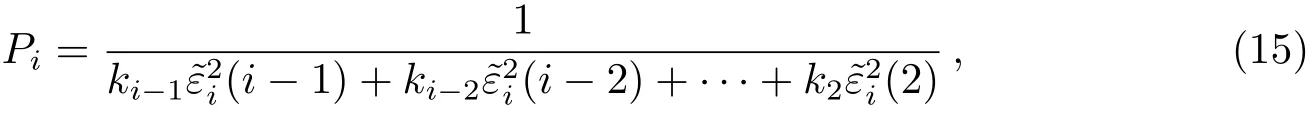
建模权是根据预报时段的前一个时段拟合误差建立的,学习权是对过去多个时段预报精度的一种表征指标.综合考虑拟合误差和预报误差对当前时段各单一模型权值的影响得到修正权,用nω表示,其定义式为[18−20]:

根据(16)式得到各单一模型的修正权,再采用(13)式的方法即可得到修正经典权组合模型的预报结果.

3 试验分析

试验数据来源于武汉大学卫星导航定位技术研究中心提供的2015-11-23–2015-12-06共14 d的连续精密钟差数据,采用4种单一模型和2种组合模型进行短期钟差预报.

目前,BDS系统在轨运行的卫星按其轨道类型分为3类,文中每类卫星各取1颗卫星的钟差数据作为试验数据,卫星号分别为C04(GEO Rb)、C07(IGSO Rb)、C14(MEO Rb).GPS系统在轨运行的卫星按卫星钟类型分为6类,每类中各取1颗卫星的钟差数据作为试验数据,卫星号分别为G04(Block IIA Rb)、G09(Block IIA Cs)、G16(Block IIR Rb)、G31(Block II-M Rb)、G27(Block IIF Rb)、G24(Block IIF Cs). 对以上9颗卫星进行试验分析,用1 d的钟差数据建立模型,共进行10次连续1 d的预报.将预报结果与精密钟差产品进行比较,来评估每种模型的预报精度.

3.1 单一预报模型分析

采用上述9颗卫星2015-11-23–2015-12-06共14 d的连续精密钟差数据作为试验数据,各颗卫星的钟差序列如图1所示.

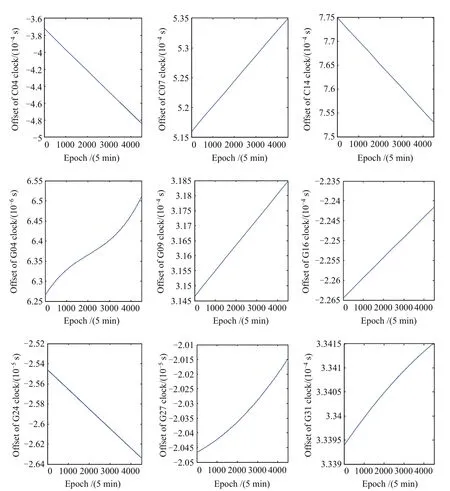
图1 各颗卫星钟差数据序列图(2015-11-23—2015-12-06)Fig.1 Data sequence diagram of satellite clock difference(2015-11-23—2015-12-06)

分别采用2015-11-23–2015-12-05单日的钟差序列作为各模型的建模序列,依次预报2015-11-24–2015-12-06单日的钟差序列,共进行10次连续1 d的预报.对几种预报模型的比较文中主要采用均方误差来衡量其预报精度,均方误差计算公式为

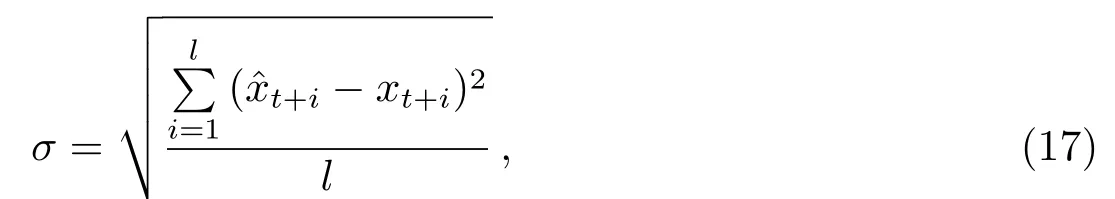
式中,l为预报历元个数.

3.1.1 多项式模型分析(QR)

对于铯原子钟(Cs)宜采用1次多项式进行拟合预报,铷原子钟(Rb)宜采用2次多项式进行拟合预报.文中采用2015-11-23单日的数据建立多项式模型,预报2015-11-24的钟差序列.

统计多颗卫星连续10次1 d的拟合和预报均方误差,统计结果如图2所示.然后分别将各颗卫星的10次拟合和预报的均方误差取平均值,得到统计结果如表1所示.

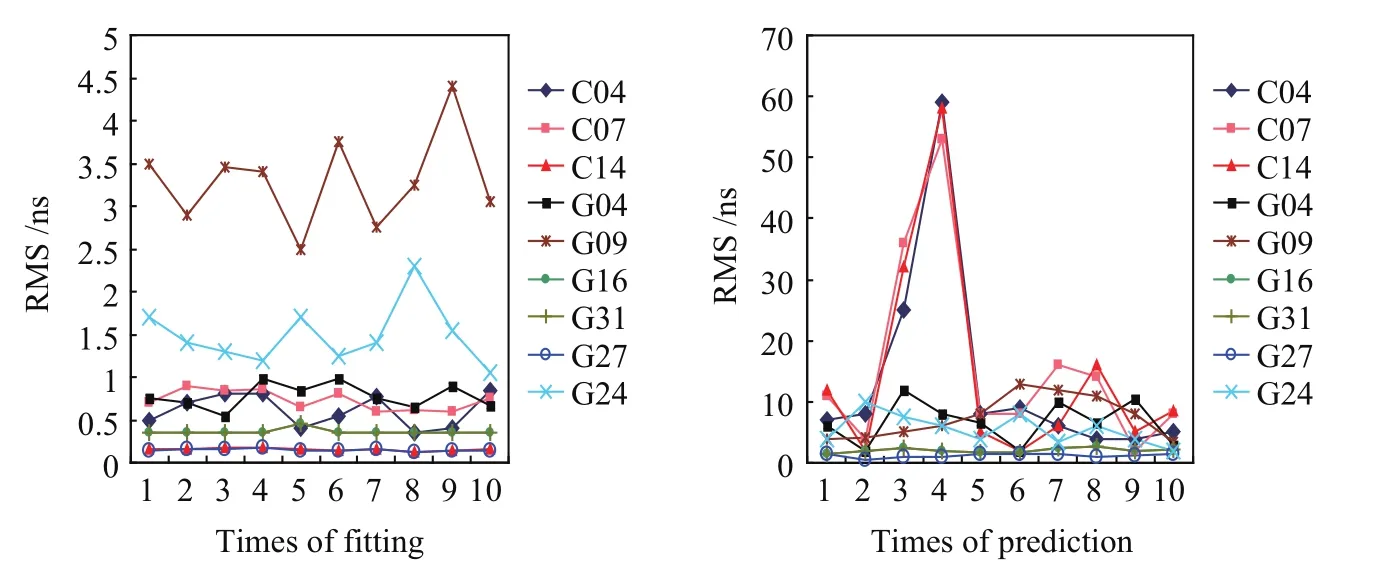
图2 QR模型拟合(左)和预报(右)的RMS值统计Fig.2 RMS statistics of fitting(left)and prediction(right)of the QR model

表1 QR模型拟合和预报的RMS值平均值统计Table 1 The average RMS statistics of fitting and prediction of the QR model

根据图2左图QR模型的拟合结果,可以看出G09(Block IIA Cs)和G24(Block IIF Cs)号卫星拟合均方误差较大,其余卫星的拟合均方误差均在亚纳秒级.图2右图的预报结果和表1的统计结果表明,对于不同卫星的钟差序列,QR模型的预测结果差异较大.G27(Block IIF Rb)号卫星钟的多个单天预报精度的平均值达到1.21 ns.利用QR模型对BDS卫星钟进行短期预报,其平均预报精度在14 ns左右,总体预报效果均差于GPS卫星钟.

3.1.2 灰色模型分析(GM)

对9颗卫星建立灰色模型,统计多颗卫星连续10次1 d的拟合和预报均方误差,统计结果如图3所示.然后分别将各颗卫星的10次拟合和预报的均方误差取平均值,得到统计结果如表2所示.

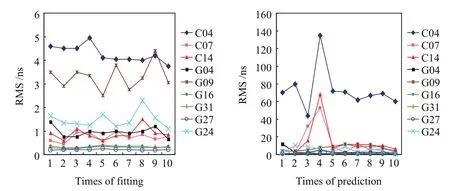
图3 GM模型拟合和预报的RMS值统计Fig.3 RMS statistics of fitting and prediction of the GM model

表2 GM模型拟合和预报的RMS值平均值统计Table 2 The average RMS statistics of fitting and prediction of the GM model

由图3和表2分析可知,对于钟差变化不稳定的序列(如C04号卫星钟),GM模型预报1 d的精度较差,其平均预报误差最大达到73 ns.而对于GPS卫星钟,GM模型对G16(Block IIR Rb)卫星钟进行连续多个单日预报,其预报精度的平均值在1 ns以下.总体预报效果BDS卫星钟均差于GPS卫星钟.

3.1.3 时间序列模型分析(ARMA)

钟差序列一般都具有明显的趋势项,是非平稳序列.需要通过1次差分的方法对数据进行平稳化处理,再采用动态数据建模方法(DDS)建立ARMA模型,即为ARIMA(p,d,q)模型,其中d=1[20].

统计多颗卫星连续10次1 d的拟合和预报均方误差,结果如图4所示.然后分别将各颗卫星的10次拟合和预报的均方误差取平均值,得到统计结果如表3所示.

表3 ARMA模型拟合和预报的RMS值平均值统计Table 3 The average RMS statistics of fitting and prediction of the ARMA model

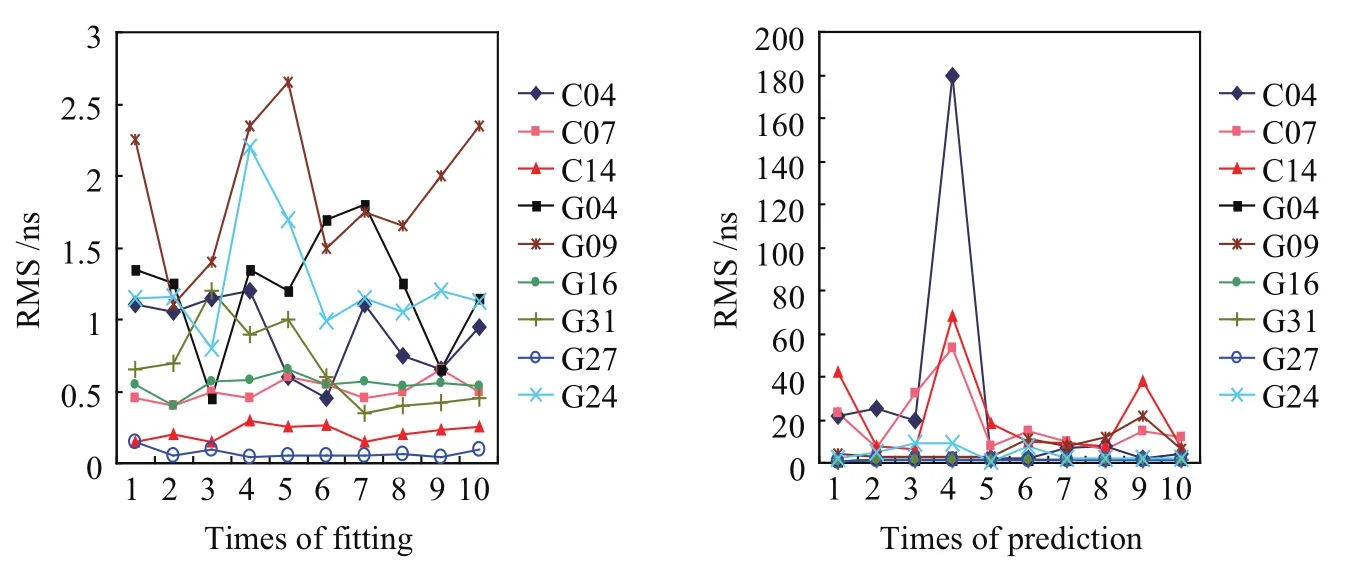
图4 ARMA模型拟合和预报的RMS值统计Fig.4 RMS statistics of fitting and prediction of the ARMA model

由图4和表3分析可知,对于BDS卫星钟,C04号卫星钟钟差序列变化不稳定,ARMA模型预报1 d的精度较差,其平均预报误差达到27 ns.而对于GPS卫星钟,ARMA模型分别对G09(Block IIA Cs)和G24(Block IIF Cs)卫星钟进行连续多个单天预报,其预报精度的平均值稍大,其余GPS卫星钟钟差序列变化稳定.总体预报效果BDS卫星钟均差于GPS卫星钟.

3.1.4 广义回归神经网络模型分析(GRNN)

利用广义回归神经网络进行钟差短期预报,在进行广义回归神经网络建模前,需先对钟差数据进行差分处理,再对其进行网络训练,最后得到的拟合和预报数据累加还原为最终的拟合和预报钟差序列.

统计多颗卫星连续10次1 d的拟合和预报均方误差,统计结果如图5所示.然后分别将各颗卫星的10次拟合和预报的均方误差取平均值,得到统计结果如表4所示.

图5 GRNN模型拟合和预报的RMS值统计Fig.5 RMS statistics of fitting and prediction of the GRNN model

由图5和表4分析可知,对于BDS卫星钟,3种类型的卫星的卫星钟钟差序列变化都不稳定,说明了训练数据的异常状态会严重影响GRNN模型预报的精度.而对于GPS卫星钟,其预报精度都在6 ns以内,其中,G16(Block IIR Rb)号卫星连续多个1 d平均预报精度达到亚纳秒级.总体预报效果BDS卫星钟均差于GPS卫星钟,甚至差距较大.

表4 GRNN模型拟合和预报的RMS值平均值统计Table 4 The average RMS statistics of fitting and prediction of the GRNN model

3.1.5 单一模型综合对比分析

单一模型对单颗卫星进行连续10次1 d的预报可以得到10个均方误差,分别对这10个值取平均值(¯σ)和取最大均方误差与最小均方误差求极差(ε=σmax−σmin)作为表5和表6中的预报精度指标.为了便于直观分析每种模型对每种类型卫星钟的预报精度情况,图6和图7分别给出了单一模型预测精度统计图和预测均方误差的极差统计图.

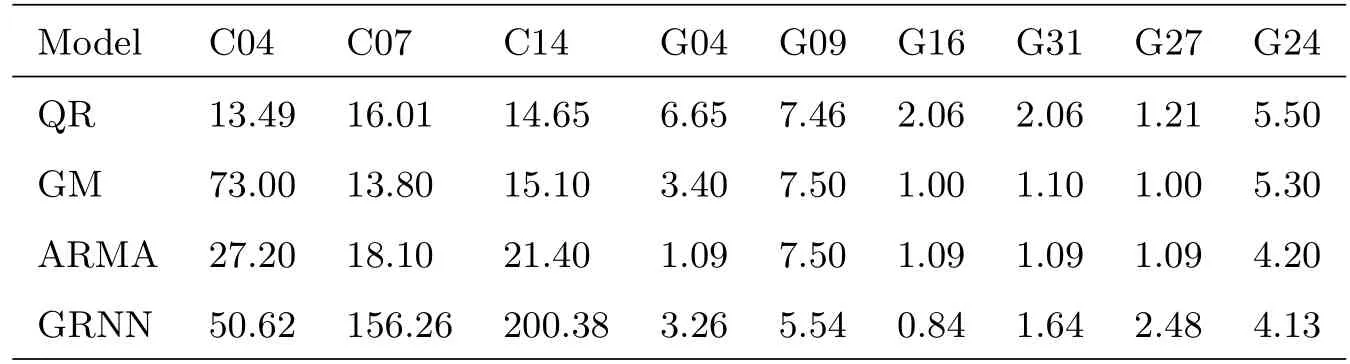
表5 单一模型预测精度对比(单位:ns)Table 5 Comparison of prediction accuracy of single model(unit:ns)

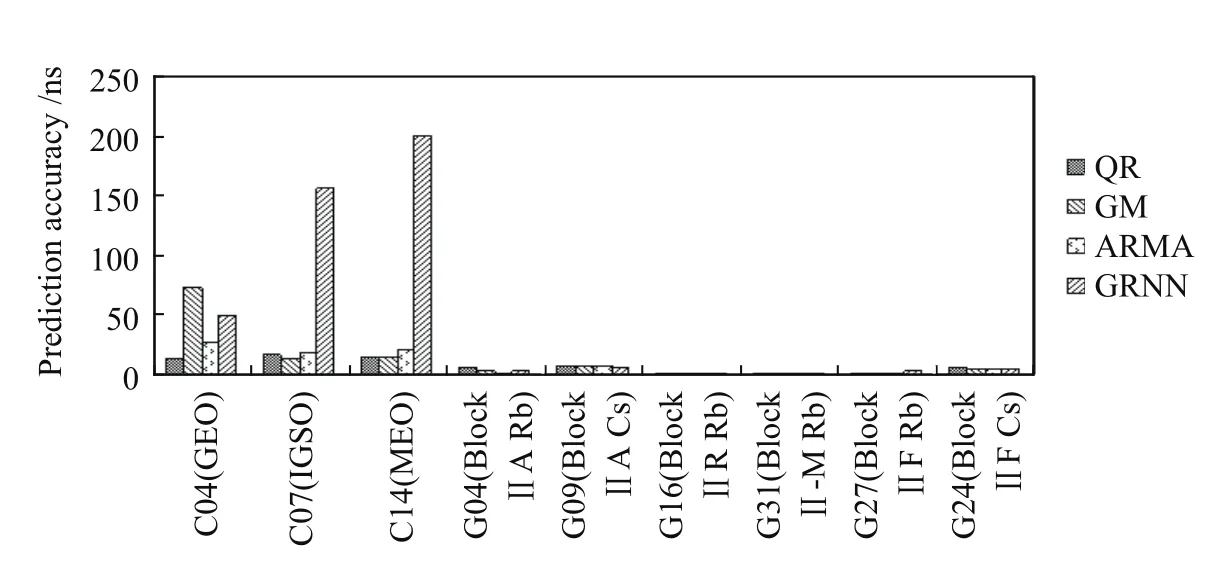
图6 单一模型预测精度统计图Fig.6 The statistical chart of the prediction accuracy for single model

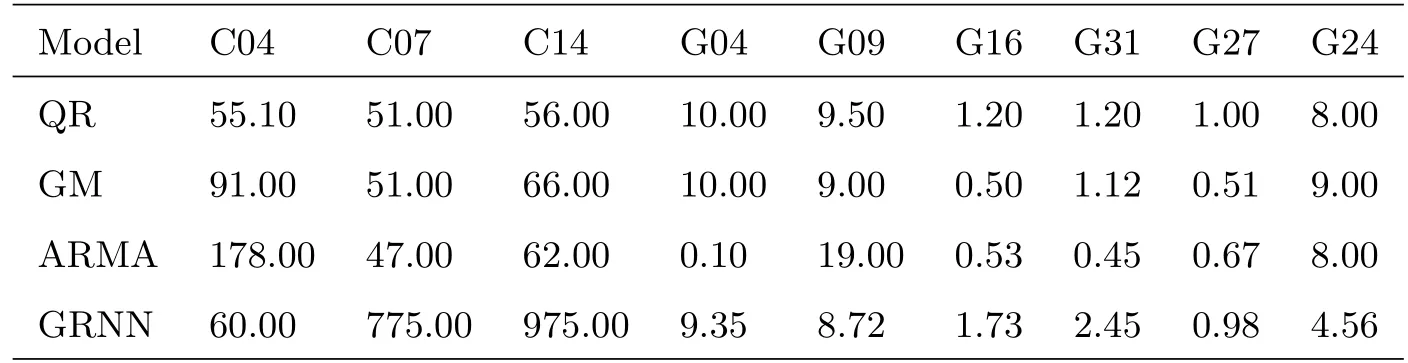
表6 单一模型预测均方误差的极差对比(单位:ns)Table 6 The range contrast of RMS for single model prediction(unit:ns)

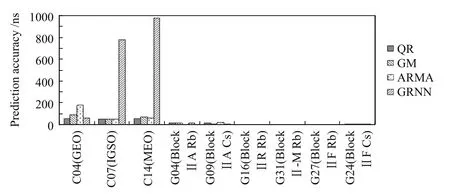
图7 单一模型预测均方误差的极差统计图Fig.7 The range statistical chart of RMS for single model prediction

结合表5、表6以及图6、图7分析可知:(1)比较分析4种单一模型在不同卫星钟的预报效果,其精度差异较大.因此,应该根据卫星钟的特点及模型的适用性,对不同的卫星选择合适的预报模型;(2)从不同模型对同一颗卫星钟的预报精度来看,对于GPS卫星钟,4种模型基本可以达到相同量级的预报精度.针对BDS卫星钟,QR、GM和ARMA 3种模型基本可以达到相同的预报效果,而GRNN模型的预报效果较差;(3)GNRR模型均方误差的极差值在BDS卫星钟预报中基本都处于60 ns以上,说明神经网络模型在钟差序列状态异常多变的情况下预报精度不稳定.与QR、GM和ARMA 3种模型预报精度对比,用GNRR模型在一部分GPS卫星钟的短期钟差预报中可以得到较稳定且高精度的结果(如G16(Block IIR Rb)、G27(Block IIF Rb)号卫星).

3.2 组合预报模型分析

综合以上所述4种模型的预报结果来看,其钟差序列变化不稳定,难以获得稳定且高精度的短期预报结果.因此,这里对于组合预报模型的研究主要针对6颗GPS(G04(Block IIA Rb)、G09(Block IIA Cs)、G16(Block IIR Rb)、G31(Block II-M Rb)、G27(Block IIF Rb)、G24(Block IIF Cs))卫星钟进行短期预报分析,不再对BDS卫星钟进行深入讨论.

采用武汉大学卫星导航定位技术研究中心提供的2015年11月23日至2015年12月6日共14 d的连续精密钟差数据,预报方案为用1 d数据进行建模并预报1 d,连续进行10次1 d的预报试验.分别采用经典权方法和修正经典权方法对4种单一预报模型(QR、GM、ARMA和GRNN)的预报结果进行组合,得到经典权组合预报模型和修正经典权组合预报模型.文中从6颗GPS卫星中选取了4颗(分别为G16(Block IIR Rb)、G24(Block IIF Cs)、G27(Block IIF Rb)、G31(Block II-M Rb))卫星精密钟差序列进行试验,得到6种模型连续多次预报的均方误差,统计结果如图8所示.表7为各卫星在单一模型和组合模型下连续10次1 d预报得到的综合精度对比统计结果,主要通过3个指标来衡量(¯σ、σ和ε).

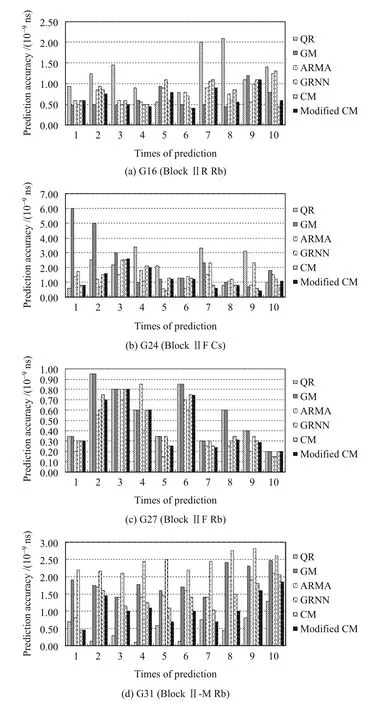
图8 单一模型和组合模型预报GPS卫星钟的精度统计图Fig.8 The statistical chart of GPS satellite clock accuracy for single model and combined model prediction

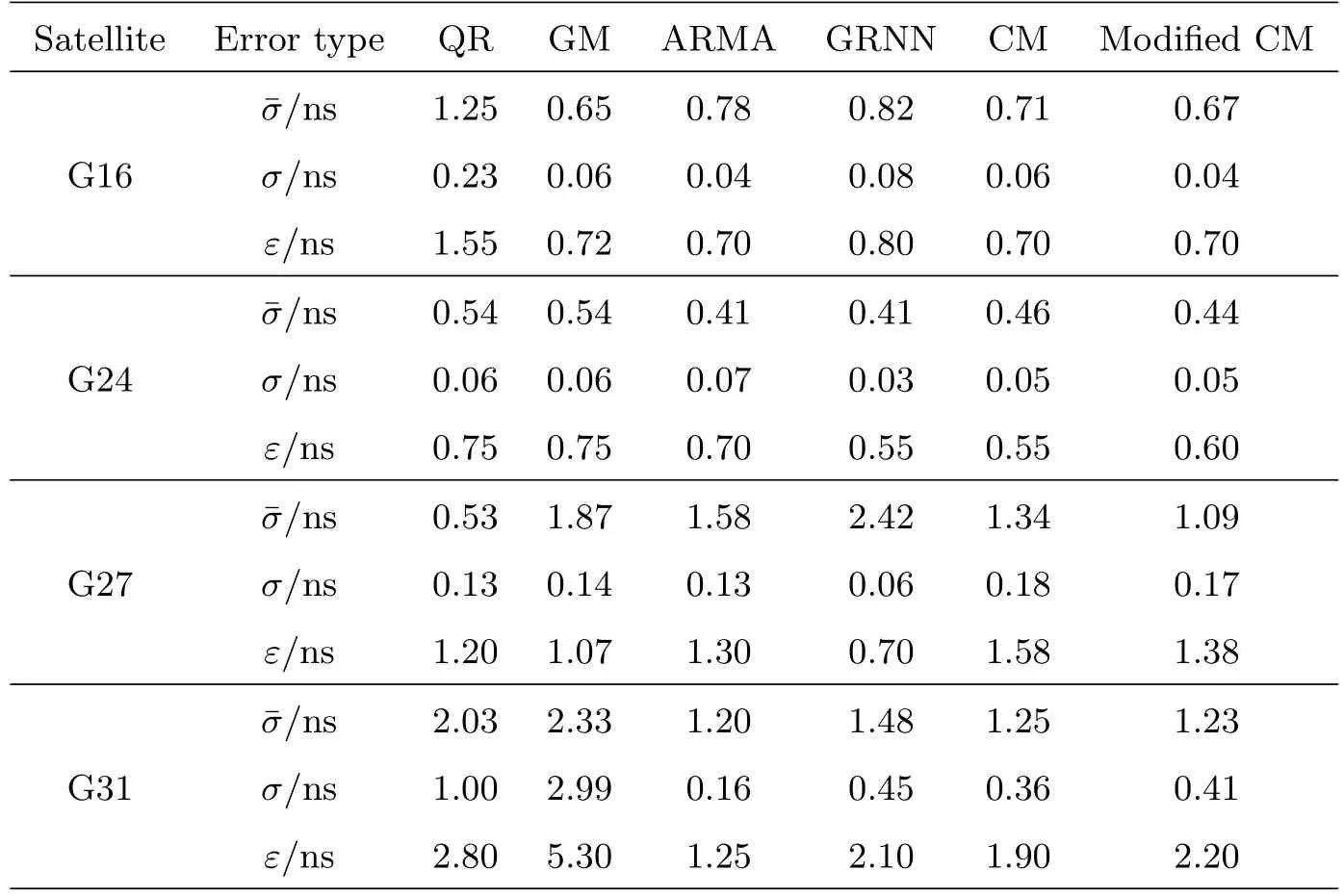
表7 单一模型和组合模型预报GPS卫星钟的精度统计结果Table 7 The statistical results of GPS satellite clock accuracy for single model and combined model prediction

结合图8和表7分析可知:(1)G16(Block IIR Rb)卫星的经典权和修正权的3个指标,修正经典权平均精度较高,预报的稳定性也较高,可以更好地平衡各单一模型的预报精度.从其他3类原子钟(G24(Block IIF Cs)、G27(Block IIF Rb)、G31(Block II-M Rb))的预报精度结果也可以得到相似的结论;(2)同一种模型应用于不同的卫星钟,其预报精度差异较大.对于G27(Block IIF Rb)卫星,QR模型精度最高,对于G16(Block IIR Rb)卫星,QR模型的预报精度最差而GM模型的预报精度相对较高;(3)在进行连续多时段预报中,修正经典权组合模型综合考虑了拟合误差以及多个历史时段的预报误差,因此其预报精度在一定程度上优于经典权组合模型,该方法在保证预报可靠性的前提下提高了预报精度.综合上述分析得出结论:线性组合模型算法简单实用,是单一模型的凸组合.该种组合模型的预报精度不会大于由单一模型预报得到的最大均方误差,甚至有时还会得到优于所有单一模型的预报精度.

4 结论

本文主要对BDS/GPS星载原子钟的短期钟差预报模型的建模特点以及6种模型(QR模型、GM模型、ARMA模型、GRNN模型、经典权组合模型和修正经典权组合模型)的预报效果进行比较分析,得出如下结论:

(1)单一模型在连续10次短期预报中,3颗BDS卫星钟(C04(GEO Rb)、C07(IGSO Rb)、C14(MEO Rb))的钟差预报精度跳跃性很大,各单一预报模型在10次连续预报中的极差均至少在50 ns以上,这也间接反映了BDS钟差数据变化规律的不稳定;而对于6颗GPS卫星钟G04(Block IIA Rb)、G09(Block IIA Cs)、G16(Block IIR Rb)、G31(Block II-M Rb)、G27(Block IIF Rb)、G24(Block IIF Cs)的预报精度变化比较平稳,各单一预报模型在10次预报中的极差最大值不高于19 ns.因此,数据本身对其预报效果影响很大.

(2)同一种预报模型应用在不同类型的卫星钟序列中,预报精度差异较大.因此,应该根据卫星钟特点以及模型的适用性,对不同的卫星钟选择合适的预报模型.

(3)通过对比不同模型的预报效果,在钟差序列状态多变的情况下,GNRR模型容易受到严重影响,导致其预报精度较差,对于C14(MEO Rb)卫星钟预报的极差值达到975.00 ns;对于G27(Block IIF Rb)卫星钟,4种单一模型中预报精度最高的是QR模型,符合G27号卫星钟差序列的变化趋势.

(4)分别采用经典权和修正经典权组合模型对钟差序列进行预报,修正经典权可以得到比经典权预报稳定性更高的结果.并且该组合模型的预报均方误差不会大于由单一模型预报得到的最大均方误差,甚至有时还会得到优于所有单一模型的预报精度.

本文主要针对BDS/GPS星载原子钟的短期钟差预报模型进行研究,而对BDS/GPS卫星钟差的中期和长期预报的规律进行研究和分析,将是下一步研究工作的重点.

致谢感谢审稿专家在审阅本文的过程中指出的问题和给出的详细建议.感谢武汉大学卫星导航定位技术研究中心提供的BDS和GPS卫星精密钟差产品数据.

[1]黄观文.GNSS星载原子钟质量评价及精密钟差算法研究.西安:长安大学,2012

[2]余航.BDS/Galileo星载原子钟性能及短期预报算法研究.西安:长安大学,2015

[3]张清华,隋立芬,贾小林,等.导航定位学报,2014,2:46

[4]马卓希,杨力,贾小林.大地测量与地球动力学,2017,37:292

[5]Breakiron L A.A Kalman Filter for Atomic Clocks and Timescales.Proceedings of the 33th Annual Precise Time and Time Interval Systems and Applications Meeting,Long Beach,November 27,2001

[6]Breakiron L A.Kalman Filter Characterization of Cesium Clocks and Hydrogen Masers.Proceedings of the 34th Annual Precise Time and Time Interval Systems and Applications Meeting,Reston,December 3–5,2002

[7]Epstein M,Freed G,Rajan J.GPS IIR rubidium clocks:In-orbit Performance Aspects.Proceedings of the 35th Annual Precise Time and Time Interval(PTTI)Meeting,San Diego,December 2–4,2003

[8]王国成,柳林涛,徐爱功,等.测绘学报,2014,43:803

[9]程瑞江,陈西宏,刘赞,等.测绘科学,2017,42:25

[10]张首刚.时间频率学报,2009,32:81

[11]贾小林,冯来平,毛悦,等.时间频率学报,2010,33:115

[12]王彬.BDS在轨卫星钟特征分析、建模及预报研究.武汉:武汉大学,2016

[13]王宇谱,吕志平,李林阳,等.天文学报,2017,58:11

[14]付文举.GNSS在轨卫星钟特性分析及钟差预报研究.西安:长安大学,2014

[15]王宇谱,吕志平,王宁.测绘学报,2017,46:157

[16]张杰.卫星钟性能分析及钟差预报.西安:西安电子科技大学,2013

[17]刘帅,贾小林,孙大伟.武汉大学学报(信息科学版),2017,42:277

[18]王继刚,胡永辉,何在民,等.天文学报,2011,52:54

[19]Wang J G,Hu Y H,He Z M,et al.ChA&A,2011,35:318

[20]田婕.GPS/BDS原子钟性能分析及钟差预报模型研究.西安:长安大学,2015