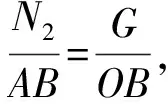高中力学中极值问题解法的探讨①
(山东省肥城市第一高级中学,山东 肥城 271600)
在高中力学习题中,经常遇到求物理量的极值问题,这会涉及力学量的临界问题,解决此类问题的基本思维方法是假设推理法,即先假设条件成立,从而把比较隐蔽的临界条件或各种可能性“暴露”出来,然后再根据物理规律及有关知识列方程求解,主要有以下几种方法。
1 解析法


图1
例1:如图1所示,摆球质量为m、摆长为L的单摆由水平状态开始下摆,在摆到竖直状态的过程中,摆球所受重力的瞬时功率如何变化?何处取得最大值?
解析:摆球所受重力的瞬时功率P用重力G和重力方向的速度vy的乘积表示,即P=Gvy,开始时摆线在水平状态,摆球初速度为零,重力的瞬时功率为零,当摆线到达竖直状态时,摆球速度虽然最大,但方向沿水平方向,竖直方向的分速度为零,故重力的瞬时功率仍为零。由此可见,摆线由水平状态开始下摆,在到达竖直状态的过程中,摆球所受重力的瞬时功率从零增大、再减小到零,此过程中重力的瞬时功率存在最大值。究竟何处最大呢?我们不妨设θ为摆线与水平方向的夹角,此时摆球速度为v。
点评:本题讨论了小球摆动过程中的瞬时功
率问题,利用三角函数展开讨论是一种重要的常规方法,在三角函数的处理过程中,巧妙地利用数学不等式能快速地求解极值问题,并避免陷入了一种“想当然”的误区。
2 三角函数法


图2
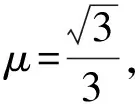

点评:三角函数配角法求极值是数学中常用的方法,它在物理问题解决中有着较为广泛的应用价值。根据物理问题用三角函数列出方程后,将三角函数中的自变量进行配角,整理化成两角和的正弦或余弦,便能得到函数的极值。当得出的式子不是典型的函数类型时,可通过等效变换进行转化,利用三角函数公式把所列的方程简化,变成仅含单个三角函数的式子,然后利用三角函数的性质解决问题。
3 图解法
图解法是一种利用几何图形解决物理问题的方法,解答共点力的动态平衡问题时常用图解法,其优点是简捷、方便、直观。可以化繁为简,化难为易,提高解题的效率。
如用三角形定则分析力的最小值:① 当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2取最小值的条件是两分力垂直。如图3甲所示,F2的最小值F2min=Fsinθ。
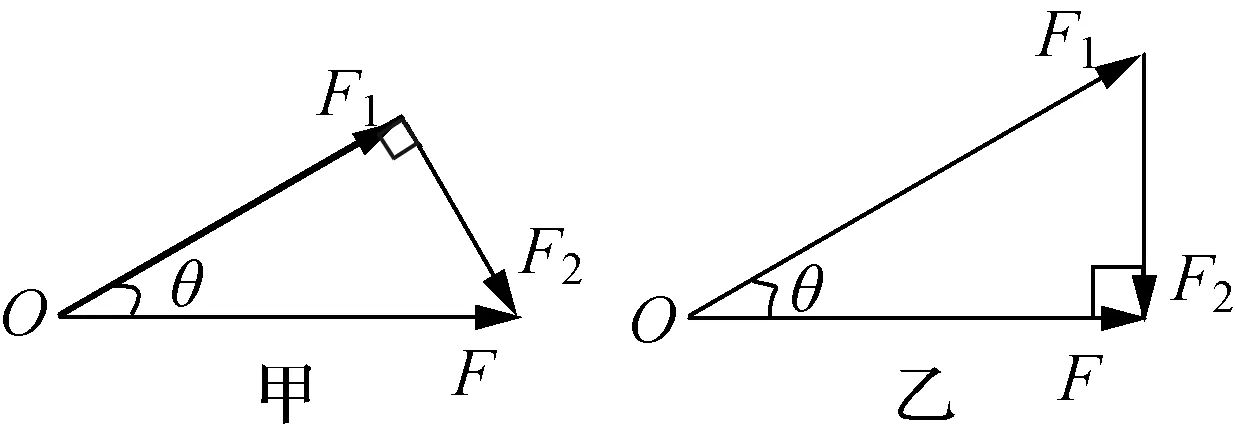
图3
② 当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2取最小值的条件是所求分力F2与合力F垂直,如图3乙所示,F2的最小值F2min=F1sinθ。
③ 当已知合力F的大小及一个分力F1的大小时,另一个分力F2取最小值的条件是已知大小的分力F1与合力F同方向,F2的最小值为|F-F1|。

图4
例3:如图4所示,半径为R,质量为m的均匀球体紧贴竖直墙壁放置,在球体的左下方有一厚为h的木块(h 图5 点评:本题求解球体脱离地面时水平推力的最小值,采用了三角形定则,把问题转化为矢量三角形的临界条件。用三角形定则解题是一个比较方便、直观地计算最小值的方法,而矢量运算始终贯穿整个高中物理的学习过程,掌握好三角形定则在解题中的应用技巧,将使学生的解题能力得到提升。 综上所述,应用数学知识处理物理问题是高考考查的能力之一,灵活地运用多种数学方法求解物理的极值问题,是中学物理教学的难点,在平时的教学中,应高度重视,及时总结,适时渗透数学思想。 [1] 丁勇.高中物理常见的极值问题解法探究[J].课程教育研究,2016,(21). [2] 周宏建.例析高中物理极值问题的求解方法[J].中学生数理化,2016,(11). [3] 鲁信.高中物理极值问题求解的两种思路[J].新高考(高三理化生),2013,(2).