航行于碎冰区船舶冰阻力与冰响应探析

王超，封振，李兴，李鹏

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

0 引 言

船舶在碎冰区航行时，有的碎冰会沿船体表面运动至桨前流场中与螺旋桨发生相互干扰，从而影响其水动力性能，甚至产生严重的振动与噪声。为了避免螺旋桨受到破坏，开展冰的运动轨迹和冰桨干扰相关研究对船舶安全性与可靠性有着重要意义。由于冰区环境的复杂性和不确定性，船舶所受的冰阻力不仅取决于船舶的船型和航速，还与海冰的类型、厚度等参数有关。自20世纪70年代以来，国内外已有许多学者针对冰—船相互作用的过程进行过研究［1-9］，主要手段是进行模型试验，但未见对碎冰的运动响应进行相关探索的文献。为此，本文拟针对碎冰的运动响应这个关键点，运用相关软件对其进行仿真计算。

从冰的形态上考虑，冰主要包括2种：平整冰和碎冰。其中，有关船舶在平整冰中航行的研究已有很大进展，而对于其在碎冰区航行的研究尚处于起步阶段。碎冰在流体的作用下其运动状态将发生很大的改变，这种改变会使得桨前流场更加不均匀，从而加剧螺旋桨工作环境的复杂性。而冰在运动至桨盘面之前首先会与船体发生接触碰撞，碰撞的结果就是改变冰的运动状态，因此研究冰与船体之间的相互干扰问题有着极其重要的意义。为了更好地模拟碎冰，本文将主要采用离散元办法（Discrete Element Method，DEM）对其进行建模，系统分析碎冰沿船体的运动状态以及船体的受力情况。

1 理论基础

20世纪70年代初，Cundalland Strack教授首次提出了离散元方法（DEM）［10］，并不断得到学者的关注和发展。离散元方法在我国起步较晚，1986年，王泳嘉在第一届全国岩石力学数值计算及模型试验讨论会上首次向我国岩石力学与工程界介绍了离散元方法的基本原理及几个应用例子，随后，离散元法在我国迅速发展起来［11-12］。

离散元方法是基于分子动力学原理发展的一种数值分析方法，专门用来解决不连续介质问题。该方法的基本思想是将离散介质看成是一系列离散单元的集合，并且每两个离散单元之间都通过相应的节点进行连接。离散元方法的一般求解过程为：首先，将需要求解的物体模型离散为离散元单元阵，并根据实际问题选取合理的连接元件将相邻两单元连接起来；其次，将相邻两单元间发生的位移作为基本变量，根据力与相对位移的关系，可得到两单元间法向和切向作用力；然后对单元在各个方向上与其他单元间的作用力，以及其他物理场对单元作用所引起的外力求合力和合力矩，之后根据牛顿运动第二定律求得单元的加速度；最后对其进行时间积分，进而得到单元的速度和位移。由此，便得到所有单元在任意时刻的速度、加速度、角速度、线位移和转角等物理量。

以简单的颗粒单元为例，对离散元方法的基本方程进行具体分析。相邻两颗粒间的受力如图1所示。图中，nij为第i个颗粒与第j个颗粒之间的连线向量。

根据牛顿第二定律，可得在每一个时间步长N内，颗粒单元应满足的方程为：

式中：mi为单元i的质量；vi为单元i形心的速度矢量；为单元i与单元j的接触力；为单元i受到的其他合外力；为单元i自身的受力；Ii为单元i的转动惯量；ωi为单元i的角速度矢量；为单元i与单元j之间的切向接触力；rij为单元i与单元j的作用点到单元i形心间的距离；为旋转弹簧产生的力矩；为受到的外力矩。

在进行离散元求解时，其重点与核心部分是对单元间接触力的求解。而单元间发生接触的判定条件为：dij＜ri+rj，即单元间形心距离小于两单元半径之和。接触力和转动力矩的增量可由下式得出：

式中：kn，ks，kθ分别为法向刚度系数、切向刚度系数和转动刚度系数；cn，cs，cθ分别为法向阻尼系数、切向阻尼系数和转动阻尼系数；分别为法相位移增量和切向位移增量；Δθi为转动角增量。

用离散元进行求解时，各单元间变形时的几何关系可由单元间法向及切向的相对位移来体现，具体表达式如下：

式中，nji表示由单元j指向单元i的单位法向量。由上式可得法向与切向的相对位移速率为：

2 计算前处理

选取离散元中的颗粒离散元模型对冰进行模拟，根据冰本身的材料特性将其分解为若干个颗粒单元，考虑冰块的尺寸特征及空间结构进行单元间的排列组合，并且颗粒单元间通过并行连接模型按照一定的排列规则连接为一个整体，组成了不同大小的单块冰模型。由于冰本身的力学性质较复杂，在进行模拟时，对其中的几个重要参数进行了设定：冰密度取为850 kg/m3，弹性模量E=2 GPa，泊松比υ=0.3。

在计算过程中选取了某冰区船作为计算模型，其主要参数如表1所示。

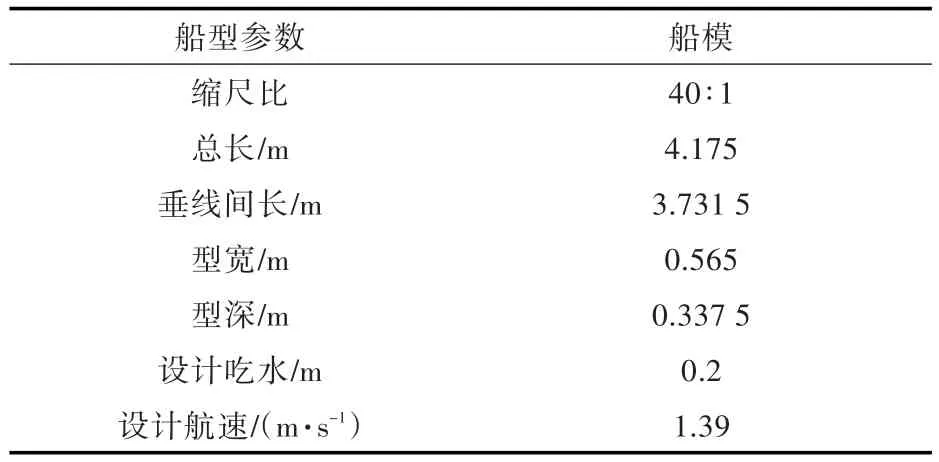
表1 某冰区船船型参数Table 1 The parameters for a certain ice ship

首先，用STAR-CCM对船模型进行网格划分，其中在船艏与船艉处由于变化曲率较大，需对其进行网格加密处理，另对水线面及冰与船体接触的部分也需要进行网格加密，以便更好地进行数据传递（图2）。然后，运用DEM颗粒模型建立冰模型。这里选取2种冰模型尺寸：一种是由颗粒组成的冰排模型，尺寸为0.05 m×0.05 m；一种是水分子形状的不规则冰（图3）。

图3 中的冰模型颗粒通过在入口处设置的发射器进入计算区域，并且在设置DEM颗粒时需考虑颗粒间的碰撞，因此针对各项之间的相互作用可设置5种作用力，把船体当作壁面且不发生变形。计算时，选取了60%，80%和90%这3种碎冰密集度下船舶所受的冰阻力及碎冰的运动情况。碎冰的分布密度是通过改变发射器的数量以及发射速率来实现的。其中：当碎冰的密集度为60%、航速为1 m/s时，只选择第1种冰块模型，具体实现方式为在入口处宽度1 m范围内分布20个发射器，发射速率设置为12个/s，如图3（c）所示；而当碎冰密集度为80%与90%时，计算域则包括以上2种碎冰模型，并通过不同的配比来实现密集度分布。

3 计算结果分析

冰区航行船舶受到的总阻力远大于开敞水域下船舶的阻力，而航行于平整冰区船舶所受的阻力又要大于航行于碎冰区船舶的阻力，其主要原因在于平整冰与船接触时会发生挤压与弯曲变形，等到破冰完成后，部分船体又相当于在碎冰区航行。航行于碎冰区域的船舶受到的冰阻力主要有清冰阻力和摩擦阻力，其中清冰阻力指船舶在航行时与碎冰发生碰撞，使其远离船体运动而产生的力；摩擦阻力指碎冰沿着船体表面运动，与船体表面之间产生的摩擦力。

本文主要计算碎冰密集度为60%，80%和90%这3种冰分布密度，以及航速为0.2，0.4，0.6，0.8，1.0，1.2 m/s这6种情况下，船舶所受的冰阻力及碎冰的运动情况。

3.1 船体阻力分析

首先，对航行于碎冰区船舶所受的总阻力进行计算，并根据计算结果以及开敞水域下船舶的阻力值得出碎冰阻力值。具体计算结果如图4和图5所示。

由图4可知，在选取的多种计算工况下，船体总阻力随航速的增大而增大，且在同一航速下碎冰密集度越大，船体的总阻力也越大。图5示出了3种碎冰密度下，船体所受总阻力与开敞水域船阻力的差值，即船舶受到的碎冰阻力。由图可知，随着航速的增加，碎冰阻力也增加，碎冰密集度越大，冰阻力越大。在碎冰阻力中，清冰阻力受航速的影响较大。当低航速航行时，碎冰与船体碰撞的接触力较小，摩擦阻力占主要部分，因此低航速时影响船体总阻力的主要是摩擦阻力；随着航速的增加，船体与碎冰之间的碰撞加剧，导致清冰阻力迅速增大；但随着航速的增大，碎冰阻力的增长趋势变缓，这主要是因为航速增加时，船体周围的兴波明显，对周围的碎冰有一定的排斥作用，致使其远离船体表面运动，这就大大降低了碎冰与船体接触和碰撞的概率，从而减小了摩擦阻力和清冰阻力。

3.2 碎冰沿船体的运动分析

船体阻力的增加是由碎冰与船体的相互作用产生的，反过来，船体的作用将影响碎冰的运动状态。因此，下文将深入讨论碎冰的运动轨迹。主要选取了特定工况下不同时刻船艏处碎冰的运动状态进行分析。计算工况选为碎冰密集度80%，航速1.0 m/s。

由图6知，当船舶驶入碎冰区域时，船艏与碎冰首先发生碰撞，碰撞部分的碎冰速度突然减小，甚至是出现负值，这是因为船舶在向前航行时对碎冰产生了一个向前的碰撞力，由此不难想象在航速较大时，碎冰会由于船体的撞击力而向前飞出。随后，碎冰沿船体表面向两侧滑动，并对航行区域以外的碎冰产生一定的挤压作用，从而加大船体周围的碎冰密集度。当碎冰运动到船后某位置时，速度又开始逐渐增大，并且碎冰的运动将对船体周围流场产生一定的影响。

图7更加直观地展现了碎冰速度因受到船体作用而发生的改变。碎冰在与船艏底部刚接触时，接触部分的速度突然变小，且明显小于周围未接触部分；当碎冰沿着船体表面运动到船艏与平行中体过渡处时，速度突然增大，并有远离船体表面运动的趋势，其原因是船体表面型线在此处有突变，并且该处的压力也会随之变化，形成肩波系，从而使得该处的流体速度变大，对碎冰有一个加速的作用。

由图8可知，船舶在碎冰区航行时，部分碎冰在船体的挤压作用下将浸没于水下，并沿船底滑动至船尾螺旋桨处。水下碎冰在沿船底表面滑动时，由于受到船底的摩擦与碰撞，将发生翻转而改变其运动状态，并使碎冰与船底的摩擦由滑动摩擦变为滚动摩擦，这也在一定程度上减小了船体的碎冰阻力。

图9与图10主要表现了船艏的兴波情况。由图10可知，船艏兴波改变了碎冰颗粒的运动状态，使得碎冰在未与船体接触前就随波飞溅而发生远离船体的运动，此状态下船艏的兴波较为剧烈，导致船体周围的碎冰数量明显低于低航速时的情况，这也就解释了为何船体所受冰阻力在航速较大时其增长会趋于平缓的原因。

4 结 论

本文主要讨论了碎冰与船体之间的相互作用关系，计算了不同航速、不同碎冰密集度下船体的受力情况，并对冰船碰撞冰时的运动响应进行了探讨，得出以下结论：

1）通过对航行于碎冰区域船体受力的分析，得出船体所受冰阻力主要是由碎冰与船体表面的摩擦和碰撞产生，并且随着航速的增大而增大；但当航速增大到一定值后，碎冰阻力不再增加，甚至有减小的趋势，这主要是由于航速较高时受船舶兴波的作用，使得船体周围的碎冰密集度减小，进而降低了冰船碰撞的概率。

2）从对冰船干扰工况下冰的运动响应的讨论中可以看出，碎冰在与船体发生碰撞时其运动状态将发生很大的改变。有些碎冰将从船艏处浸入到水线面以下，并沿船底表面向后运动至船后螺旋桨处，这些碎冰不仅改变船体周围的流场，也使得螺旋桨前方的进流更加不均。

3）在航速较高时，船艏的兴波将迫使碎冰远离船体运动，从而减小了船舶的碎冰阻力。由此可以得出，良好的船型表面不仅可以降低无冰时的总阻力，也可以减小碎冰阻力。

本文在选用DEM颗粒时，选择的物理模型较少，与实际工况相比还存在一定的差距，并且工况的选择也需要更加接近于实际，同时，也未计算船—桨一体工况下碎冰的运动响应，因此下一步将对船—桨一体时碎冰的运动进行计算分析。

［1］JANSSON J E． Ice-breakers and their design［M］.［S.l.］： European Shipbuilding， 1956： 112-128，143-151.

［2］KASHTELJAN V I，POZNJAK I I，RYBLIN A J.Ice resistance to motion of a ship［M］.Leningrad：Marine Computer Application Corporation，1969.

［3］LINDQVIST G.A straightforward method for calculation of ice resistance of ships［C］//10th International Conference，Port and Ocean Engineering under Arctic Conditions.Luleaa，Sweden：［s.n.］，1989.

［4］Finnish-Swedish ice class rules［S］.Finnish and Swedish Maritime Administration，2002.

［5］SPENCER D.A standard method for the conduct and analysis of ice resistance model tests［J］.［S.l.］：NRCC，Institute for Marine Dynamics，1992.

［6］SPENCER D，JONES S J.Model-scale/full-scale correlation in open water and ice for Canadian coast guard［J］.Journal of Ship Research，2001，45（4）：249-261.

［7］王超，康瑞，孙文林，等.平整冰中破冰船操纵性能初步预报方法［J］.哈尔滨工程大学学报，2016，37（6）：747-753.WANG C，KANG R，SUN W L，et al.Preliminary forecasting method for icebreaker maneuverability on level and smooth ice［J］.Journal of Harbin Engineering University，2016，37（6）：747-753（in Chinese）.

［8］季顺迎.寒区海洋工程中离散元方法的应用［C］//2014年全国环境力学学术研讨会论文摘要集.天津：中国力学学会，2014.

［9］季顺迎，李紫麟，李春花，等.碎冰区海冰与船舶结构相互作用的离散元分析［J］.应用力学学报，2013，30（4）：520-526，645.JI S Y，LI Z L，LI C H，et al.The discrete element analysis of the interaction between sea ice and ship structure in broken ice area［J］.Chinese Journal of Applied Mechanics，2013，30（4）：520-526，645（in Chinese）.

［10］CUNDALL P A，STRACK O D L.A discrete numerical model for granular assemblies［J］.Géotechnique，1979，29（1）：47-65.

［11］王泳嘉，邢纪波.离散元法及其在煤矿开采中的应用（第2讲）［J］.煤矿开采，1993（4）：56-58.

［12］李紫麟.船舶在碎冰区航行的离散元模型及冰荷载分析［D］.大连：大连理工大学，2013.