抛物线定义显神奇

■河南省潢川县第一中学高三(3 1)班 张家源

在解析几何中,抛物线问题的求解往往离不开抛物线的定义。抛物线的定义不仅能帮助我们打开解题思路,而且可以减少计算量,真可谓“抛物线定义显神奇”。

一、定义助我求轨迹

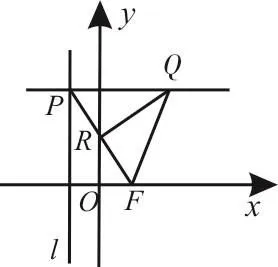
图1

解析：依题意知,点R是线段F P的中点,且R Q⊥F P,故R Q是线段F P的垂直平分线。

点Q在线段F P的垂直平分线上,则|P Q|=|Q F|。又|P Q|是点Q到直线l的距离,故动点Q的轨迹是以F为焦点,l为准线的抛物线,其方程为y2=2x(x＞0)。

评注:解答本题的关键是发现|P Q|=|Q F|,动点Q的轨迹满足抛物线的定义。

二、定义助我求方程

图2

解析：分别过A,B作A A1⊥l于A1,B B1⊥l于B1。由抛物线的定义知|A F|=|A A1|,|B F|=|B B1|。

因为|B C|=2|B F|,所以|B C|=2|B B1|,∠B C B1=3 0°。连接A1F,则△A A1F为等边三角形。过F作F F1⊥A A1于F1,则F1为A A1的中点。设l交x轴于K,则|KF|抛物线方程为y2=3x。

评注:求抛物线的标准方程就是求参数p的值,这个值可根据抛物线的定义并借助于几何法求得。

三、定义助我求比值

A.2∶ 5 B.1∶2 C.1∶ 5 D.1∶3

解析：如图3所示,由抛物线定义知|MF|=|MH|,所以|M F|∶|MN|=|MH|∶|MN|。

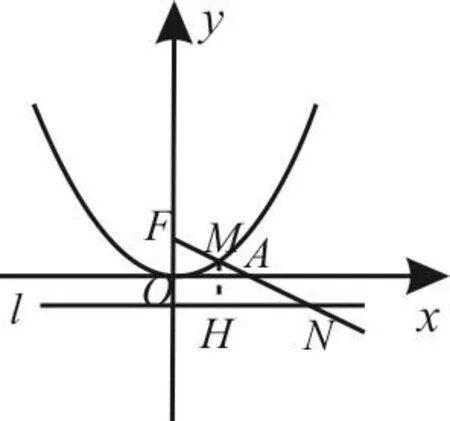
图3

评注:利用抛物线定义和图形特征,把解析几何问题转化为平面几何问题,大大减少了计算量。

四、定义助我求最值

解析：分析可知A点在抛物线内部,如图4。设抛物线上点P到准线l:x距离为d,由定义知|P A|+|P F|=|P A|+d。当P A⊥l时,|P A|+d最小,此时P点的纵坐标为2,代入y2=2x,得x=2,故点P的坐标为(2,2)。

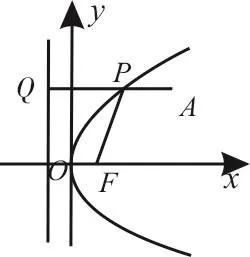
图4

评注:与抛物线有关的最值问题,一般情况下都与抛物线的定义有关。“看到准线想焦点,看到焦点想准线”,这是解决抛物线焦点弦有关问题的重要途径。

五、定义助我求面积

解析：P Q过焦点,|P Q|可看成两个焦半径之和。

如图5,不妨设抛物线方程为y2=4a x,P(x1,y1),Q(x2,y2),则由抛物线定义知|P Q|=|P F|+|Q F|=x1+a+x2+a=x1+x2+2a=b。

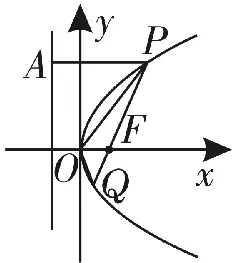
图5

故x1+x2=b-2a。又由于P Q为过焦点的弦,因此y1y2=-4a2。

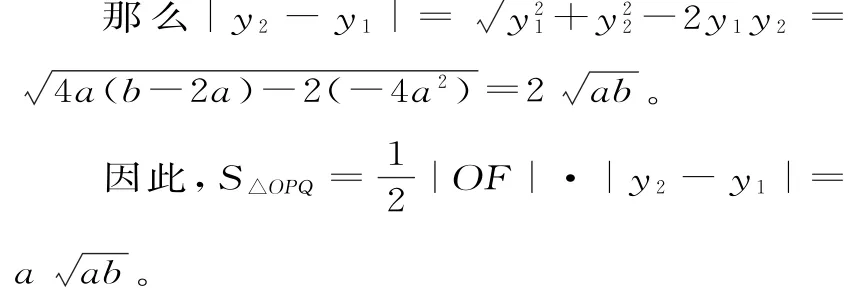
评注:将焦点弦分成两段,利用定义将焦点弦长用两端点横坐标表示,结合方程,利用根与系数的关系是常见的基本技能。本题计算三角形面积的技巧,是求解抛物线问题中经常用到的,同学们要注意掌握。

(责任编辑 徐利杰)