链接高考中的离心率问题
■山东省枣庄二中 王 真
一、高考考情
高考中的离心率问题重点考查离心率及其取值范围,以及圆锥曲线的几何意义等知识。常见题型有两种:一种是求圆锥曲线的离心率;另一种是利用离心率求参数的取值范围。
(1)椭圆:e∈0,1();
(2)双曲线:e∈(1,+∞)。
2.圆锥曲线中a,b,c的几何性质及关系。
(1)椭圆:a2=b2+c2。
①2a:长轴长;
②2b:短轴长;
③2c:椭圆的焦距。
(2)双曲线:c2=b2+a2。
①2a:实轴长;
②2b:虚轴长;
③2c:双曲线的焦距。
3.求离心率的策略:求椭圆或双曲线的离心率主要围绕寻找参数a,b,c的比例关系(只需找出其中两个参数的关系即可)进行。
(1)利用几何性质:如果题目中存在焦点三角形(曲线上的点与两焦点的连线组成的三角形),那么可以考虑寻求焦点三角形三边的比例关系。两条焦半径与a有关,另一条边为焦距,从而可求解。
(2)利用坐标运算:如果题目中的条件难以发掘几何关系,那么可考虑将点的坐标用a,b,c进行表示,再利用条件列出等式求解。
4.离心率的取值范围问题,在寻找不等关系时通常考虑以下几个方面:
二、知识方法整合
(1)题目中某点的横坐标或纵坐标是否有范围要求,例如椭圆与双曲线对横坐标的范围有要求,如果问题围绕在“曲线上存在一点”,则可考虑该点坐标用a,b,c表示,且点坐标的范围就是求离心率范围的突破口;
(2)若题目中有一个核心变量,则可以考虑把离心率表示为某个变量的函数,从而求该函数的值域即可;
(3)通过一些不等关系得到关于a,b,c的不等式,进而解出离心率。
注:在求解离心率范围时要注意圆锥曲线中对离心率范围的初始要求:椭圆,e∈(0,1);双曲线:e∈(1,+∞)。
三、考题精选
(一)求离心率
解析:以线段A1A2为直径的圆的方程为x2+y2=a2。直线b x-a y+2a b=0与圆相切,所以圆心到直线的距离a,整理得a2=3b2。
故a2=3(a2-c2),所以答案为A。
解析:作出双曲线的右支,如图1所示,作A P⊥MN。因为圆A与双曲线C的一条渐近线交于M、N两点,所以不妨设M、N为双曲线的渐近线上的点,且A(a,0),则AM=AN=b。
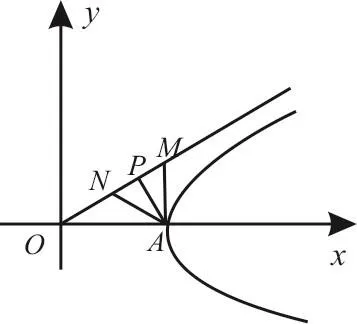
图1
由c2=a2+b2得c=2b,所以e=ac=
点评:双曲线的渐近线是其独有的性质,所以有关渐近线的问题容易受到命题人的青睐。做这一类问题要抓住以下要点:①求解渐近线,直接把双曲线后面的1换成0即可;②双曲线的焦点到渐近线的距离是b;③双曲线的顶点到渐近线的距离是
(二)已知离心率求参数
解析:因为a2=1,b2=m,所以
点评:本题主要考查的是双曲线的标准方程和双曲线的简单几何性质,属于基础题,解题时要注意a,b,c的关系c2=a2+b2。
(三)离心率的取值范围
点评:解决椭圆或双曲线的离心率的求值及范围问题的关键是确立一个关于a,b,c的方程或不等式,再根据a,b,c的关系消掉b得到a,c的关系式,要充分利用椭圆或双曲线的几何性质、点的坐标的范围等。

点评:本题根据题设条件“有相同的焦点”建立等量关系,得到函数关系式进而根据m的取值范围,借助反比例函数求解离心率的范围。
(责任编辑 徐利杰)
- 中学生数理化(高中版.高二数学)的其它文章
- 抛物线知识结构与拓展
- 抛物线中的高考题
- 对求双曲线的离心率问题的探究
- 寻找身边的抛物线
- ?如何我解决几何体的外接球问题
- 抛物线定义显神奇

