抛物线中的高考题
■河北省张家口市第二中学 王 潇
由于抛物线方程的特殊性:一个一次项,一个二次项,抛物线问题越来越受到命题专家的青睐,下面让我们一起来梳理吧。
重点题型一:抛物线的定义与平面几何的完美结合
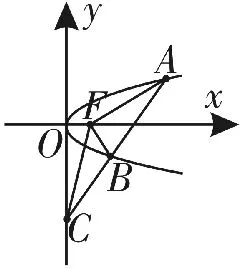
图1

试题分析:由抛物线的准线为x=-1,所以|B F|=xB+1,|A F|=xA+1,设△A C F中A C边上的高为h,则有

图2
试题分析:根据已知作图分析,如图2。
由抛物线性质知|B F|=|BM|,而已知|B C|=2|B F|,则|B C|=2|BM|,∠C BM=6 0°。又因为直线过焦点,联立解方程组可得,则此抛物线的方程为y2=9x或y2=3x。
梳理总结:抛物线的定义是解决抛物线问题的基础,它能将两种距离进行等价转化。如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么应考虑应用抛物线的定义。如果题目再与平面几何综合起来,就有一定难度了,需要我们熟练掌握初中的平面几何知识,才可以顺利解决这类有一定难度的题目。
重点题型二:抛物线定义与最值的完美结合
试题分析:如图3直线x=-1为抛物线的准线,点P到直线x=-1的距离等于到焦点F(1,0)的距离,由三角形两边之差小于第三边知|P F|-|P Q|≤|Q F|,当P,Q,F三点共线时,P F与P Q的距离之差最

图3
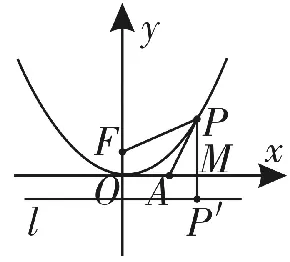
图4

梳理总结:利用抛物线的定义可实现由点到点的距离与点到直线的距离的转化。我们常常利用“两点之间线段最短”,“三角形两边之和大于第三边”,“三角形两边之差小于第三边”等,将问题转化。
重点题型三:抛物线与定值的巧妙结合

图5
试题分析:由题知直线AM,BM的斜率存在且不为0,设直线MA的方程为y-3
因为直线MA,MB的斜率互为相反数,所以直线M B的方程为

试题分析:(1)由题意知,A(1,1),B(4,-2),设点P的坐标为(xP,yP),切线l1:y-1=k(x-1),联立物线与直线l1相切,解得。联立l,1l2的方程,解得x,故点P

梳理总结:解析几何中的定值问题是指某些几何量的大小或代数表达式的值等和题目中的参数无关,不依参数的变化而变化,始终是一个确定的值。而在抛物线中,特殊的就是点的设法,根据方程的特点灵活设出点的坐标,如上例中设点M(,y0),再根据抛物线方程的特殊性:一个一次项,一个二次项,从而可求出定值。
重点题型四:抛物线与取值范围问题的巧妙结合

试题分析:F(1,0),设A(x1,y1),B(x2,y2),由题设y2)=λ(1-x1,-y1)。

联立①、③解得x2=λ,依题意有λ>0。
所以B(λ,2λ),或B(λ,-2λ),又F(1,0),得直线l的方程为:
(λ-1)y=2 λ(x-1),或(λ-1)y=-2λ(x-1)。

梳理总结:对于范围问题,一般可以利用数形结合或转化为函数的最值来求解。其本质还是由于抛物线方程的特殊性,如例9中可得x2=λ,从而将所求问题转化。这种现象,在椭圆或者双曲线中是不可能出现的,点的坐标都是很复杂的,所以求解椭圆或双曲线问题时最常用的方法是设而不求,整体代入。而抛物线中则可以把点的坐标简洁表示。
抛物线还有很多常见而特殊的题型,例如直线与抛物线的位置关系,抛物线的定点问题等。当然,对于抛物线问题我们也不能完全掉以轻心,因为抛物线也有很复杂的题目哟!
(责任编辑 赵 平)

