寻找身边的抛物线

■河南省潢川高级中学高三(2 1)班 刘紫阳

生活中充满了数学,数学就在我们周围。在足球比赛时,猛一脚射门,足球沿着一条美丽的弧线,球进了,那将是激动人心的事。这其实就是抛物线。只要我们细心观察生活,就会发现生活中有很多与抛物线有联系的事物,甚至导弹轨迹也与抛物线有一定的联系,下面我们一起来赏析几例。

一、隧道中的抛物线

某隧道横断面由抛物线及矩形的三边组成,尺寸如图1所示,某卡车空车时能通过此隧道,现载一集装箱,箱宽2m,车与箱共高4.5m,问此车能否通过此隧道,说明理由。

图1

解析：建立如图2所示的平面直角坐标系,则B(-3,-3),A(3,-3)。

设抛物线方程为x2=-2p y(p＞0),将B点的坐标代入,得9=-2p·(-3),故线方程为x2=-3y(-3≤y≤0)。

图2

因为车与箱共高4.5m,所以集装箱上表面距抛物线形隧道拱顶0.5m。

设抛物线上点D的坐标为(x0,-0.5),D′的坐标为(-x0,-0.5),则x20=1.5,解得x0=

二、喷泉中的抛物线

如图3所示,水池中央有一喷泉,水管的长|O′P|=1m,水从喷头P喷出后呈抛物线的形状,先向上至最高点后落下,若最高点距水面2m,点P距抛物线的对称轴1m,则水池的直径至少应设计为多少?(精确到个位)。

图3

解析：如图4所示,建立平面直角坐标系。

设抛物线的方程为x2=-2p y(p＞0)。

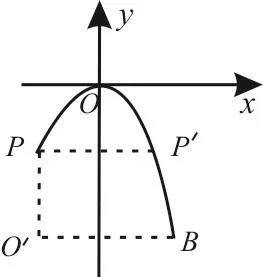
图4

设B(x,-2),则x=2,|O′B|=1+2。

故水池的直径为2(1+2)≈5(m),即水池的直径至少应设计为5m。

三、酒杯里的抛物线

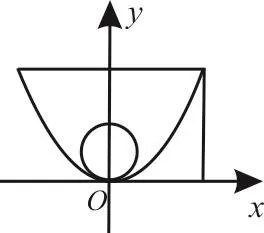
图5

解析：在酒杯轴截面内,玻璃球成了位于抛物线内的一个圆,以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,如图5所示。

则抛物线方程可设为x2=2p y(p＞0),依题意得点(2 1 0,2 0)在抛物线上,故4 0=2p×2 0,p=1,抛物线的方程为x2=2y(0≤y≤2 0)。

若玻璃球触及杯底,圆与x轴切于原点,这时圆心坐标为A(0,r),在抛物线上任取一点P(x,y),则|A P|2=x2+(y-r)2=y2+2(1-r)y+r2=[y+(1-r)]2+2r-1≥r2。

则1-r≥0,0＜r≤1。

故当玻璃球的半径r取值范围为(0,1]时,才能使玻璃球触及杯底。

从以上几例可以看出,求解生活中的抛物线问题的关键,是合理建立直角坐标系,将几何问题转化为代数问题来解决,体现了解析几何的“特殊功能”,也体现了数形结合的“神奇力量”。

(责任编辑 徐利杰)