小学数学游戏化学习的课程建构

王素旦

摘要：在数学游戏化学习中体验感悟，积累经验，是顺应时代脉搏，更是提升数学素养的重要方式，但还没有引起普遍重视。目前，数学缺少系统的游戏化活动设计、游戏化学习组织指导等。从数学课程时间分割和空间打造入手，让数学更贴近儿童，建立游戏化学习的教学操作范式和游戏化学习的评价机制，有助于推动数学思维走进数学游戏化学习，有助于培养学生核心素养。

关键词：游戏化学习;课程建构;小学数学

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2018）12A-0076-04

融游戏于数学中从古就有，早已不是新鲜事物，但是在信息增长日新月异的今天来重提，有着崭新的时代意义，更是基于儿童学习立场的有力回归。加拿大學者巴格利曾经分析了2004年到2012年期间发布的《地平线报告》，指出其中先后提出了37项新技术，但是只有7项被后期的4份《地平线报告》证实，这7项中基于游戏的学习居于首位[1]。小学数学游戏化学习的课程建构可从以下方面入手。

一、空间“物化”

（一）游戏角落

游戏角落将教室物化的空间一分为三，分为课程教学区、学习探究区和游戏角落区，从口袋数学到游戏角落，同班同学“不同学”（不同学习进度、不同学习内容）。游戏空间可以是潜能学生的操作辅导空间，也可以是学生的差异发展空间，让不同学生在数学上尝试实现不同的发展，更多地了解数学，发现数学，玩转数学。在游戏角落中配套有两个不同年段进度的iPad，内存相应的数学闯关游戏App、数学动画等，此外还配备了观察类、推理类、计算类、解决问题类数学游戏器具，展示了数学谜语等。

（二）数学步道

游戏步道将数学融于校园实景中，让学生充分感受到数学接上了生活的地气。走廊空间有多长？金苹果楼正面的玻璃幕墙有几块？学生餐厅凳子有几张？旗杆有多高？井盖上的毕加索系列（了解简单的形体）等等，让学生在现实的浓厚氛围中亲近数学，感知数学，学习数学，运用数学，自主建构生长智慧。

（三）数学场馆

数学实验室、魅力数学馆的每一个工具都值得学生好好把玩，每一个体验性游戏项目都吸引学生去思考，去探究。结合班级“小问号”，学生有诸多的数学未解之谜，室外走廊相邻班级间有电子屏可以供他们探究、汇报、发布成果。

二、时间“递化”

我们基于数学学科内在逻辑结构，基于儿童的学习规律和儿童好玩的天性，先后多次调整，最终使数学游戏化学习的时间顺次演变，实现时间“递化”。

（一）调节式衔接课程

心理学家有关儿童注意力的稳定性持续时间的统计数据显示：5～6岁儿童注意力集中时间约为10～15分钟，7～10岁儿童注意力集中时间约为15～20分钟，10～12岁儿童注意力集中的时间约为25～30分钟，12岁以上儿童能集中注意力超过30分钟。我们基于刚进入小学的低年级学生注意力的随意性和抗干扰能力相对较差的现状，关注低年级幼小衔接情感特点和学生注意力集中的认知特点，结合数学教材的教学进度，一方面进行收集，另一方面开发课前、课中、课尾游戏操。具体开展时间根据教学内容和班级基础而定，如“10以内的分与合”课前进行“扑克碰碰碰”游戏，可以让不同层次、不同熟练程度的学生都参与到游戏中来，关注差异性和实效性。在“认识前后左右”课中进行反口令练习，既可以多感官巩固已有方位概念，又能在轻松愉悦中提高学生的注意力。

（二）主题式学园课程

课题组在精读苏教版十二册数学教科书，并对其他教材有所涉猎，有了大的教材观前提下，深入挖掘其中游戏元素，按“数与代数”“空间与图形”等四大领域来研读，掌握各练习训练点之间的内在联系，让苏教版小学数学教材实现价值最大化和知识结构化。课题组还尝试梳理了一至五年级与教材同步并契合学生相应认知和年龄特点的一些数学游戏，如：“数与运算”模块的“舒尔茨方块”“手指对对碰”“数陷阱”等游戏，“模式与关系”模块的“数天平”“接头暗号”等游戏。

（三）融合式常态课程

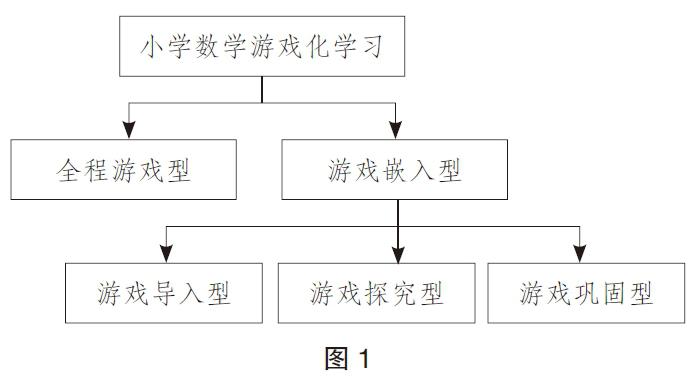
40分钟的数学课堂依然是培养学生学科核心素养和关键能力的主要抓手。我们把小学数学游戏化学习与国家数学课程进行整合，在通读对比多个版本教材的基础上，灵活设置数学游戏化学习结构，根据游戏在课堂环节中的占比把融合式常态课程分为以下几种类型（如图1）。

三、内容“活化”

大部分人产生负面情绪时，注意力会从学习所必需的高级认知加工中偏离。而持续性压力可导致海马和前额叶皮层的损失，会影响记忆和信息加工[3]。每一个游戏都需要遵守规则，游戏是为快乐而来，快乐就是竞争力。

（一）整体关联，全景呈现，情境与经验再现

案例1：认识线段

师：（出示苹果）今天的数学课，我们从桌上的苹果开始。

（轻轻拿起小刀，在苹果上切一刀）

师：同桌指一指，说一说，你在切的面上找到线是从哪儿到哪儿？

师：现在请大家再在刚切下的这片苹果上小心地切一刀。

师：（呈现不同成果）指一指，说一说，从这些苹果上找到的线，你能把它们分分类吗？

切苹果游戏，从立体上剥离平面，在面上寻找线，再聚类分析抽象出线段的特征，从三维到二维再到一维，游戏化的设计注重整体关联，全景式地展现了线段在图形与几何中的知识图式。从无意走向有意，从简约走向丰盈，学生充分在情境中实现知识体系的自我建构，形成体系化而非碎片化的网络。

（二）精选素材，核心聚焦，实践与智慧共生

案例2：圆的认识

材料：（同桌一套2副）磁性小白板、牵线白板笔、强磁贴（系在线的另一端）

要求：用以上材料进行画圆

圆的两个核心要素是定点与定长，教师在学生纯熟掌握画圆技能的基础上，安排一套有猫腻的游戏道具，直接导致学生画出的圆不够圆，引发学生思考，从而发现失败的原因，更加直观地感受圆的半径是固定的。设计超乎想象，开启深度思考。教师精心选择的材料，让学生在经历失败后的愤愤不平中理性剖析反思，直指概念关键核心，实现了游戏操作与思维生长的相融共生。

（三）精致练习，差异巩固，最近与最优发展

案例3：连加连减

层次一：数学泡泡秀，屏幕上5秒出现3个数，进行连加运算，又准又快即可击中出现的泡泡。

层次二：弹珠落下来（如图2），得分取3排洞中最上面弹珠的数值，算出最终得分。

层次三：弹珠和洞形状、数量不变，弹珠上都是未知数，弹珠落下来，得分取3排洞中最上面弹珠的数值，最终得分12分，六颗弹珠分别会是哪些数？

练习中设置了三级挑战。层次一是基础性巩固练习，让每个学生都能获得成功。层次二，需要训练学生的观察发现能力和信息筛选能力。层次三，一方面是逆向推理能力的培育，一方面也是发散性思维、有序思维渗透的绝佳契机。学生有的从一开始盲目凑数，有的联系层次二获得感悟。极个别学生开始思考如何使3个数和为12，进行有序列举。从盲目，到无序，到有序，教师基于学生的最近发展区设置游戏，让学生“跳一跳”就能摘取成功的果实，在“跳一跳”后又设置“跳几跳”，不断从他们的最近发展区升格为二次最近发展区，从二次最近发展区又设置认知困难，让思维多飞一会儿，抵达最优发展区，从而实现基于差异，发挥差异，发展差异。

（四）序列优化，螺旋上升，理解与创造并行

案例4：“多边形的内角和”

观察发现边数与内角和关系，归纳出n边形内角和是（n-2）×180度。

师：陈省身教授曾在北京大学的一次讲学中说，人们常认为三角形内角和等于180度，但这是不全面的。你怎么看？

（没有意料中的喧哗，学生的眼神中充满着惊讶与疑惑，约莫过了半分钟左右，才出现窃窃私语）

生1：老师，你是说一开始就有误差，不是180度？（语气中有试探与不确定）

生2：撕一撕，拼一拼可能会有误差，量一量也会有误差，可是当时我们课上用动画演示，大家都看到形成了平角的呀，而且上面每个角也都出现数据的啊，我们还都算了几个的。

（问题没有解决，学生又陷入了进一步的思考）

生3：如果三角形内角和180度都是有问题的，那今天我们研究其他多边形都是转化成三角形来研究的呀。如果开始就是错的，那一错后面都错了。

师补充：陈省身教授对大家的疑问做出了如下解答——说三角形内角和为180度不全面，不是说这个事实不对，而是说这种看问题的方法不太对。

师启发：说看问题的方法不太对，是刚才我们一直把关注点放在了内角和上探索出了规律，找到了一个计算内角和的公式。多边形的内角和一直随着边的条数增加在变化，这是一条变化的规律。跳出内角和怎么样能从中寻找更一般性的不变的规律呢？

提示：如果看外角呢？（教师相机展示数学动画介绍多边形的外角和）

（有学生开始有所领悟，进行操作）

小結：三角形、四边形、五边形……任意n边形外角和都是360度。

聚焦内角，师生在众多变化中找到规律：n边形内角和是（n-2）×180度。而聚焦外角，师生发现任意n边形外角和都是360度，这就把多种情形用一个十分简单的结论概括起来。用一个与n无关的常数代替了与n有关的公式，找到了更一般的规律。

从一系列变化中，感受并寻找到变化的规律，再由百变中寻找不变，可以说，这样的剧情反转对于学生来说，是认知上的跨越，是学习体验中的柳暗花明。数学家波莱尔说过，数学家的目的往往是寻求一般的解，他喜欢用几个一般的公式来解决许多特殊的问题。这也正是数学简洁之美的有力见证，从特殊走向一般，走向更加普遍。从不同角度进行发散思维、求异思维，进行知识间、方法间相似模块的融通整合，理解与创造并驾齐驱。正是因为拥有这样游戏化的思维与游戏精神，不断打破旧思维，因此在背诵100以内质数表中，总有学生想着法子“偷懒”，居然找到了“窍门”：百以内质数除了2、3两个外，剩下的都是6的倍数多1或者少1。

四、评价“智化”

（一）评价内容，“乐学”与“慧教”双向建构

圈养的方式不仅导致学生不自由，也带来了教师专业成长的钝化与惰性。一本教材，三两参考书，即可行走课堂，教师失去了更多对于本文内容的独立见解与教育机智生长。以数学游戏化为契机，以评价为导向（如表1），更多的教师被吸引参与到数学游戏化课程的设计和提升“慧教”教育智慧中来。

（二）评价机制，实现现有认知的统构超越

郑毓信教授曾提醒：“如果缺乏足够自觉的话，数学固有的特性可能在各个方面导致消极的后果，包括研究思想、学术态度乃至人生哲学等。”[4]学校采用星河币这种校园代币，这在很多学校都很常见。但星河币并不仅仅代表的是积分，而是以评价触动创新，以机制撬动创生。星河创想银行总行成立，承办兑换业务，六大分行设立，推出储蓄业务、众筹共建等等，旨在构建“小学中的大学”“小学校中的大社会”。学校以星河币架构评价体系，直指文化基础、自主发展、社会参与等学生核心素养。学生在体验中培养了财商，提升了责任担当，不断积厚底蕴。学生利用闲暇时间开设“保洁公司”以提升校园整洁度和学生行为文明度，寻访小商品市场，搜索淘宝，进行预算估计，招募员工进行楼层管理，发放工资薪酬，进行账务处理，年终开展公司运营情况分析汇报。“餐厨垃圾管控小组”在21天改变习惯行动中，每天对各个班级的餐厨垃圾进行称量，进行记录统计公示。混龄的学生一起参与行动，用不同数学表征形式展现成果。低年级学生通过记录或表格整理呈现，中高年级学生用条形统计图、饼状图等直观呈现。一方面，通过这样的方式促进朋辈间的教育力量生成，另一方面，学生在合作中拥有了“数学的敏感”。对于浪费多的菜品，学生进行重点关注，如对营养不够的提出有效剔除建议，对营养菜品提出烹饪方式的改进建议。学生在一系列的自发行为中经历经验调动、建构、提升，他们的数学意识、数学能力、数学学习品质等都在游戏化评价机制的促动下自由、自主生长。

參考文献：

[1]尚俊杰，裴蕾丝.重塑学习方式：游戏的核心教育价值及应用前景[J].中国电化教育， 2015（5）：41.

[2]帕梅拉·利贝克.儿童怎样学习数学：父母和教师指南[M].方未之，译.北京：人民教育出版社，1986：4.

[3]玛丽亚·哈迪曼.脑科学与课堂：以脑为导向的教学模式[M].杨志，王培培，译.上海：华东师范大学出版社， 2018：38.

[4]郑毓信.数学教育哲学的理论与实践[M].南宁：广西教育出版社， 2008：40.

责任编辑：石萍

Construction of Game Learning Curriculum for Primary School Mathematics

Wang Sudan

（Wujin Xinghe Experimental Primary School， Changzhou 213161， China）

Abstract： Students gain perception and accumulate experience in mathematics game learning， which conforms to the pulse of the times， and also an important way of enhancing mathematics accomplishments， but it has not aroused widespread attention. Currently， mathematics is lacking in systematic game activity designing and guidance of game learning organization. Teachers should start with curriculum time division and spatial creation to let mathematics get close to children so that we can establish the teaching paradigm and assessment mechanism of game learning， helping propel mathematics thinking into game learning and cultivate students core accomplishments.

Key words： game learning; curriculum construction; primary school mathematics