以四基四能为载体 考查数学核心素养

毛德金

【摘要】 主要从“以本为本，细查教材觅题源”“以纲为纲，深研解法得真知”“以准为准，广泛联系求发展”三个方面对2017年安徽省中考压轴题进行赏析，希望能够对平时教学与中考复习有所帮助，更有效地培养学生数学核心素养.

【关键词】 压轴题;核心素养;解法研究

一、原题再现

题目  （2017年安徽卷第23题）已知正方形ABCD，点M为边AB的中点.

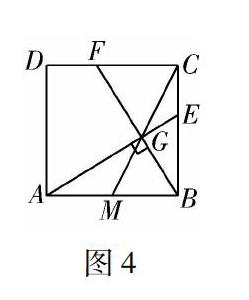
（1）如图1所示，点G为线段CM上的一点，且∠AGB=90°，延长AG，BG分别与边BC，CD交于点E，F.

① 求证：BE=CF;

② 求证：BE2=BC·CE.

（2）如图2所示，在边BC上取一点E，满足BE2=BC·CE，连接AE交CM于点G，连接BG并延长交CD于点F，求tan∠CBF的值.

从以往安徽省中考试题来看，每年试卷的最后一题（即第23题，以下代称“压轴题”）具有考查与选拔双重功能，起点低，落点高，且往往来源于教材，设计精巧，解法多样，对平时教学与中考复习具有极大的导向性，因而，备受关注.2017年安徽省中考压轴题，仍然保持了这一特点，下面从不同角度对该题进行分析与研究.

二、以本为本，细查教材觅题源

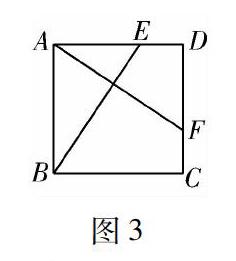
1.人教版《义务教育教科书·数学》八年级下册第68页习题8：如图3所示，四边形ABCD是一个正方形花园，E，F是它的两个门所在位置，且DE=CF.要修建两条路BE和AF，这两条路等长吗？它们有什么位置关系？为什么？

2.人教版《义务教育教科书·数学》九年级上册第18页“阅读与思考”——黄金分割数.

3.人教版《义务教育教科书·数学》九年级下册第30页教材内容：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例……

当我们依次品味上述三条与该压轴题之间的内在联系时，会清晰地看到一条来源之路：“1”中证明三角形全等是本题的起点，“2”中黄金分割数的求法是本题第（2）小题必须掌握的运算方法，“3”中所涉及的“A”字型与“8”字型相似模型是相似三角形判定的基础，在本题的图形与推理中得到充分的展示与应用.

三、以纲为纲，深研解法得真知

本题以正方形为背景，考查全等、相似、直角三角形、代数运算等知识点.从《2017年安徽省初中学业水平考试纲要（数学学科）》可查得相关考查要求分别为D（运用）或C（掌握）.本题完全按照这样的要求呈现，深入探究本题的解法对平时教学、命题以及中考复习具有极大意义.

对于第（1）题的第①小题，可用“ASA”（或“AAS”）证明△ABE≌△BCF，从而获得证明.证法略.

对于第（1）题的第②小题，主要可通过三角形相似获得证明.

思路1  结论BE2=BC·CE中的三条线段在同一条直线上，因此，考虑将有关线段转换.若能发现BE=CF=CG，则可通过证明△CGE∽△CBG获得证明.

方法1  如图4所示，因为∠AGB=90°，所以∠GAB+∠ABG=90°，

因为∠ABC=∠CBG+∠ABG=90°，

所以∠GAB=∠CBG.

又因为M为AB的中点，

所以MG=MA=MB，所以∠GAB=∠AGM.

又∠CGE=∠AGM，所以∠CGE=∠CBG.

又∠ECG=∠GCB，所以△CGE∽△CBG.

所以 CE CG = CG CB ，即CG2=BC·CE.

又由∠CFG=∠GBM=∠MGB=∠CGF，得CF=CG.

而由①知BE=CF，所以BE=CG，

故BE2=BC·CE.

思路2  若將BE2=BC·CE转换为BE·CF=BA·CE，则可通过证明△CEF∽△BEA获得证明.

方法2  如图5所示，连接EF.

因为∠FGE=∠AGB=90°，∠FCE=90°，

所以F，C，E，G四点在以EF为直径的圆上，

所以∠CFE=∠CGE.

又因为M为AB的中点，所以MG=MA=MB，

所以∠GAB=∠AGM=∠CGE=∠CFE.

又∠FCE=∠ABE=90°，所以△CEF∽△BEA，

所以 CE BE = CF BA ，即BE·CF=BA·CE.

又BE=CF，BA=BC，所以BE2=BC·CE.

思路3  建立平面直角坐标系，设BC为1，再设法算出BE，CE的长度即可得证.

方法3  如图6所示，以点A为坐标原点，边AB，AD所在直线为x轴、y轴建立平面直角坐标系，设正方形边长为1.

因为∠AGB=90°，M为AB的中点，

所以MG=MA=MB= 1 2 .

又由勾股定理得MC=  5  2 .

作GH⊥AB，垂足为H，则GH∥BC.

所以△MHG∽△MBC，

所以 MG MC = MH MB = GH CB ，

所以MH=  5  10 ，GH=  5  5 ，

所以点G的坐标为  5+ 5  10 ，  5  5  .

设直线AG的解析式为y=kx，则  5  5 =k· 5+ 5  10 ，

解得k=  5 -1 2 .