以文具为背景的数学题

文/秦丽萍

三角板、量角器、直尺、小刀是学习数学的必备文具.近些年，以文具为载体的数学题备受命题者青睐.这些题目与学生学习生活紧密相关，能激发学生的学习兴趣.请看以下例子.

一、三角尺类

例1如图1，将一副三角板和一张对边平行的纸条按下列方式摆放，两块三角板的一直角边重合，含30°角的直角三角板的斜边与纸条的一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是______．

解：如图1，过A点作AB∥a，∴∠1=∠2，

∵a∥b，∴ AB∥b，

∴∠3=∠4=30°，

而∠2+∠3=45°，∴∠2=15°，

∴∠1=15°．

例2如图2，两块全等的三角尺重叠放在△ACB的位置，将其中一块三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F.已知∠ACB=∠DCE=90°，∠B=30°，AB=8cm，则CF=______cm．

解：由已知可得，

DC=AC，∠D=∠CAB=60°，

∴∠D=∠DAC=60°，

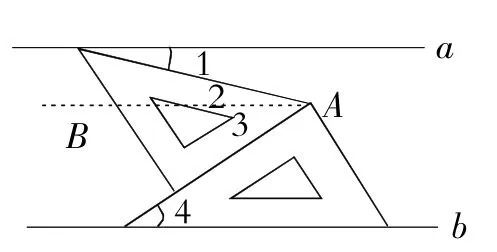
图1

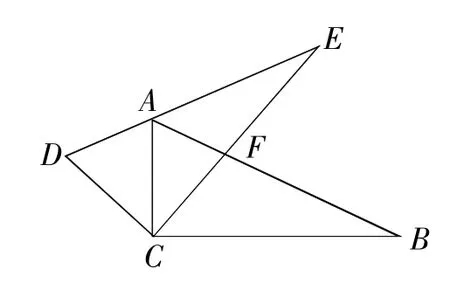
图2

∴∠DCA=60°，∴∠ACF=30°，∴∠AFC=180°-（∠ACF+∠CAF）=90°，

∵AB=8cm，∴AC=4cm，

二、量角器类

例3如图3，Rt△ABC的斜边AB与量角器的直径恰好重合，B点与0刻度线的一端重合，∠ABC=40°，射线CD绕点C转动，与量角器外沿交于点D，若射线CD将△ABC分割出以BC为边的等腰三角形，则点D在量角器上对应的度数是（ ）

A．40°. B．70°.

C．70°或80°. D．80°或140°.

解：如图3，点O是AB的中点，连接DO．

由已知可得，点C在以点O为圆，OA为半径的圆上，

点D在量角器上对应的度数为∠DOB，且∠DOB=2∠BCD，

当射线CD将△ABC分割出以BC为边的等腰三角形时，则∠BCD=40°或70°，

∴∠DOB=2∠BCD=80°或140°. 选D．

例4已知M，N，P，Q四点的位置如图4所示，下列结论中，正确的是（ ）

A．∠NOQ=42°. B．∠NOP=132°.

C．∠PON比∠MOQ大. D.∠MOQ与∠MOP互补.

解：如图4所示，∠NOQ=138°，选项A错误；

∠NOP=48°，选项B错误；

∠PON=48°，∠MOQ=42°，

∠PON比∠MOQ大，选项C正确；

∠MOQ与∠MOP不互补，选项D错误．

选C．

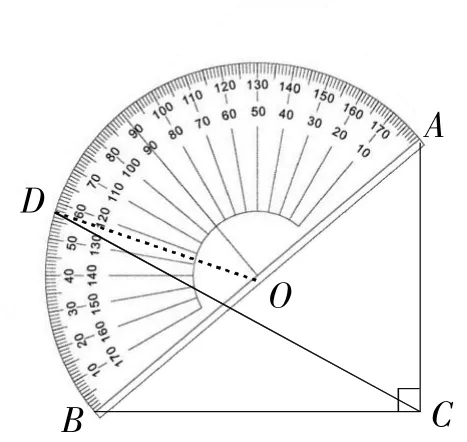
图3

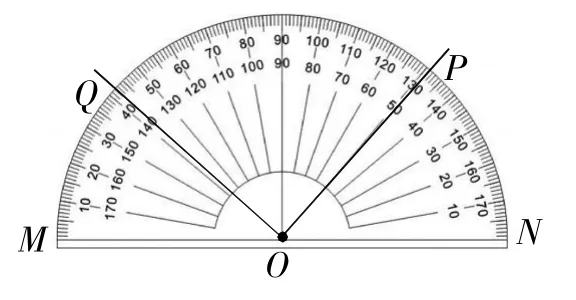
图4

三、文具刀

例4图5是我们常用的折叠式小刀，图6中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边沿线可看成两条平行的线段，转动刀片时会形成如图6所示的∠1与∠2，则∠1与∠2的度数和是______度．

解：如图6，AB∥CD，∠AEC=90°，

作EF∥AB，则EF∥CD，

所以∠1=∠AEF，∠2=∠CEF，

所以∠1+∠2=∠AEF+∠CEF=∠AEC=90°．

填90．

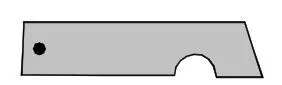
图5

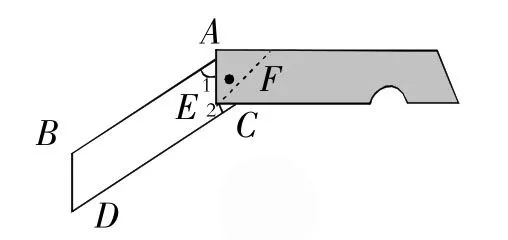
图6