基于DeepMask和RJMCMC的遗留箱体检测

刘小虎 彭天亮 邢 静

（1.西安培华学院 西安 710125）（2.南昌工程学院江西省水信息协同感知与智能处理重点实验室 南昌 330099）

1 引言

随着城市经济的高速发展，“智能监控分析系统”迅猛发展［1］，针对遗留物的检测，国内外学者给出了一些有效的方法，文献［2］将隐马尔科夫模型用于遗留包裹的检测中，并将手提包裹、放下包裹、捡起包裹等一系列人的行为特征进行分类，该方法对运动目标的检测分割部分精度要求较高，当包裹紧贴人身的时候就有可能不能准确地分割出包裹和人。

由于运动目标的交互行为造成目标和观测间的对应关系难以确定，多目标跟踪常结合贝叶斯概率推理框架来实现，粒子滤波是常用的贝叶斯推理逼近方法，文献［3］提出基于BPF滤波的多目标跟踪，使用ADaboot检测目标，结合粒子滤波实现跟踪，取得了较好的结果；蒙特卡洛方法是一种采用随机模拟采样的方法来实现后验的近似估计，文献［4］采用RJMCMC采样的方法实现了维数可变的近似推理过程，进而实现对不定目标的跟踪。而上述方法容易受到光照、形变及遮挡等的影响，本文基于深度神经网络和RJMCMC提出了一种遗留箱体检测方法：采用DeepMask［5］的深度神经网络架构，实现对场景中物体的分割及检测，并用于计算给定状态下的观测概率，以改进跟踪状态，同时采用基于RJMCMC的可变多目标跟踪算法，实现对物体状态的跟踪建模；遗留检测部分，首先根据DeepMask的检测结果和跟踪状态，初步确定遗留箱体的候选集，然后结合RJMCMC中的“新生”行为和跟踪状态，最终确定是否为遗留箱体。

2 贝叶斯模型

遗留箱体检测包含箱体分割识别及多目标追踪两个部分，整体过程采用动态贝叶斯网络模型，其主要包含两种类型的变量，第一种为隐变量，用以表征追踪过程中的状态空间，也即追踪目标的配置，记为 Xt={Xi，t，i∈It} ，i为目标索引，t={1∶T}为时间索引，其主要描述了目标的索引、类别、位置及大小等参数信息；第二种为观测变量，记为Zt，主要描述了当前帧中物体的特征等相关信息。

在建模过程引入一阶马尔科夫假设，即当前时刻t的状态 Xt只依赖于前一时刻的状态 Xt-1，同时假设在给定 Xt的情况下，到当前时刻t为止的所有观测变量 Z1∶t={Z1，…，Zt}之间相互独立，那么追踪问题就转变为在给定观测量情况下，求解当前时刻所对应状态的后验分布 p(Xt|Z1∶t)［6］，结合贝叶斯理论，后验概率可用式（1）进行计算：

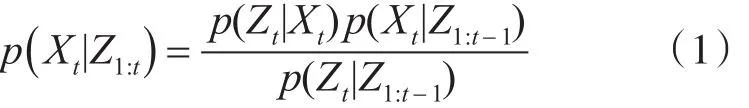
其中，p(Xt|Z1∶t-1)可用Chapman-Kolmogorov等式［15］表示为式（2）的形式：

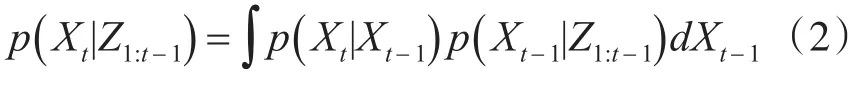
其中，p(Xt-1|Z1∶t-1)为前一时刻的后验概率，p(Xt|Xt-1)为状态转移概率，也称为预测步或动态模型。将式（2）带入式（1），同时用常量C来表示p(Zt|Z1∶t-1)，则可得到式（3）递归贝叶斯滤波方程：

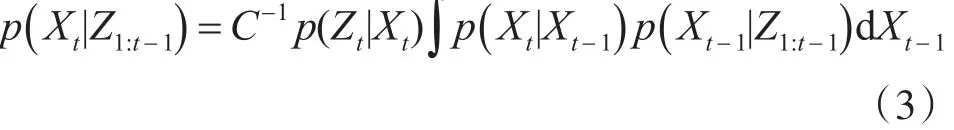
式（3）主要包含两个步骤：预测和更新。预测阶段，将当前时刻和前一时刻之间的状态转移概率p(Xt|Xt-1)和前一时刻的后验分布 p(Xt-1|Z1∶t-1) 相结合，来预测当前时刻的状态 p(Xt|Zt-1)；更新阶段，当前时刻的观测量Zt已知，使用似然概率p(Zt|Xt)来度量观测量和预测状态间的吻合程度，进而更新当前状态。

2.1 可变目标的动态模型

可变目标的动态模型对应于预测阶段中的p(Xt|Xt-1)，可表示为

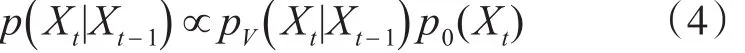
其中，pV(Xt|Xt-1)为多目标动态模型，定义为

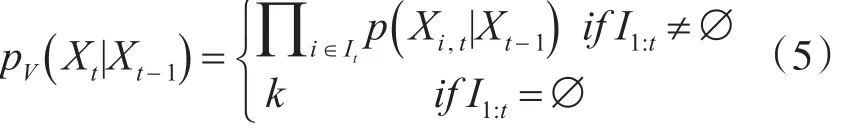
k为常数，Ø表示空集，p( )Xi，t|Xt-1为单个目标的转移概率，定义为

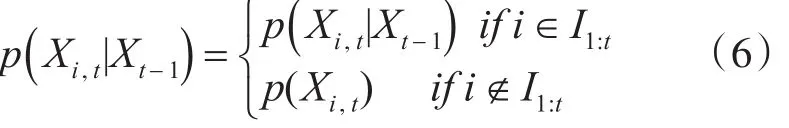
p0(Xt)为当前时刻中各目标间的交互关系，用于限制目标间的互相覆盖，可定义为

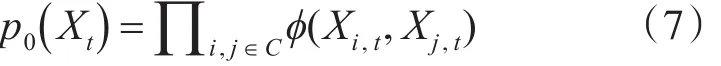
其中，ϕ(Xi，t，Xj，t)∝ exp(-g(Xi，t，Xj，t))，即基于目标紧邻间的关系来建模。

2.2 多目标联合似然模型

多目标联合似然模型对应于更新阶段中的p(Zt|Xt)，对其采用 DeepMask［5］神经网络结构进行建模，其整体框架如图1所示。

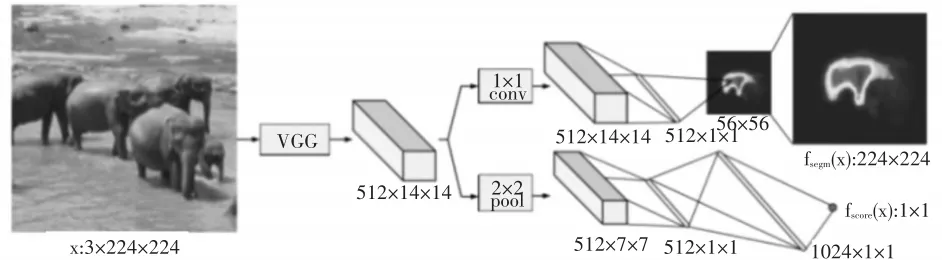
图1 DeepMask神经网络结构

其主要包含两个部分：一是获取目标候选区域，并实现对目标的分割；二是对候选区域进行目标的检测；两者之间在前期特征部分采用共享的方式实现，使得网络结构精简且效率较高，在减少候选区的同时，能够保证较高的召回率和检测精度。

该神经网络的损失函数为

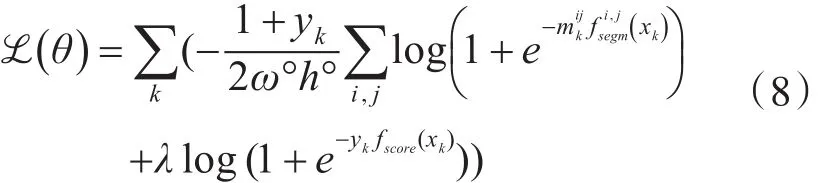
因此，在给定当前图像帧的情况下，定义多目标的联合似然函数为

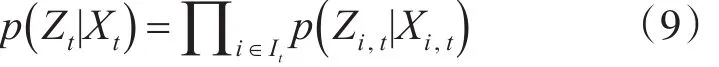
其中，p(Zi，t|Xi，t) 为在给定当前时刻状态时，观测量的似然概率值，定义为

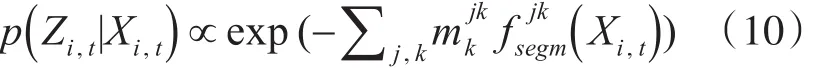
当模型状态和观测量不一致时，所得似然概率值较小，从而需要对状态进行更新以符合观测，进而实现目标的跟踪。

3 近似后验估计

在实际场景中，由于目标间的交互，使得观测量和状态之间存在多种对应关系，本文采用可逆跳转马尔科夫链蒙特卡洛（RJMCMC）［7］方法来近似求解状态的后验概率。

在RJMCMC中，任何造成维度变化的转换都必须是可逆的，一个可逆的变换定义了从当前状态X到另一提议状态 X*的转换函数hv，且hv是可微同构的，为了配置状态间的维度变化，通常需要引入附加变量U［8］，则状态 X转移到状态 X*的接受率可定义为

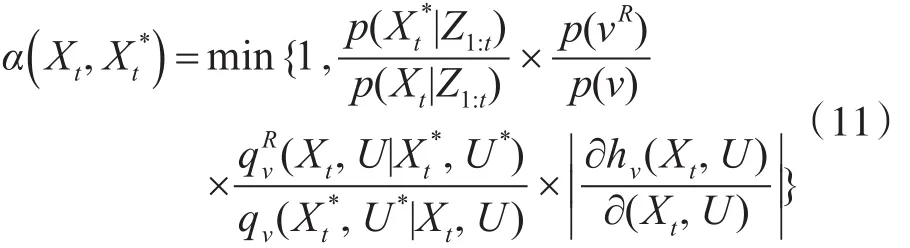
其中 p(Xt|Z1∶t)为模型的似然概率，p(v)为转换类为维度变化时的雅克比矩阵。因此，为了使得雅克比矩阵为1，设计以下三种转换方式：

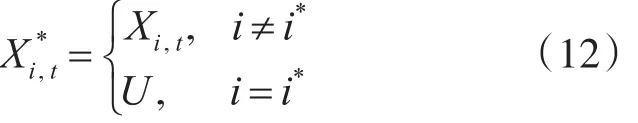
此时，其提议分布为

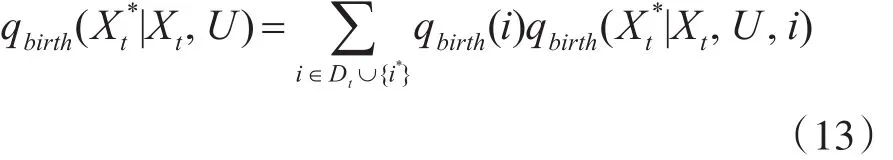
其中：qbirth(i)为新增加目标的概率，i*为可选的目标索引，Dt为当前时刻“消失”的目标，新增目标的提议分布定义为

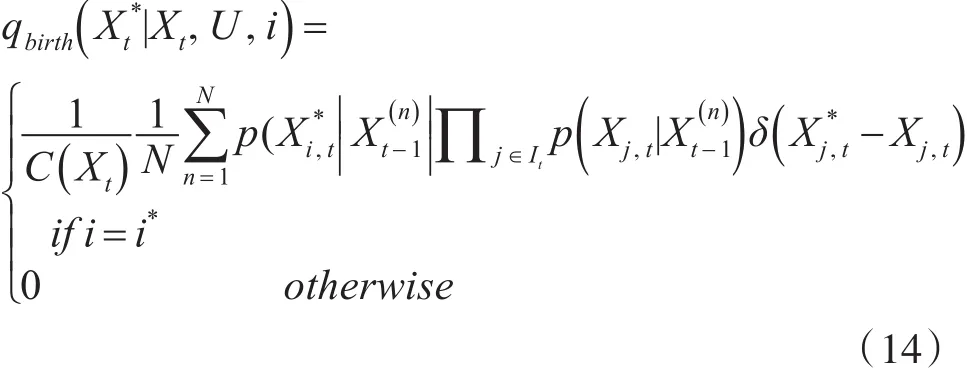
此时，采样的接受率为

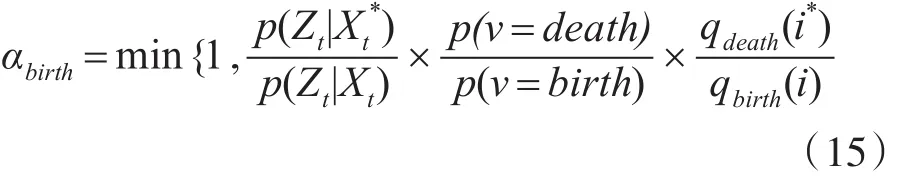
其中，p(Zt|Xt)为似然概率，p(v)为转换类型的概率，qbirth为新生概率。

2）“消失”：即从当前状态中去除一个目标，以回到之前的跟踪状态，其和“新生”转换之间是可逆

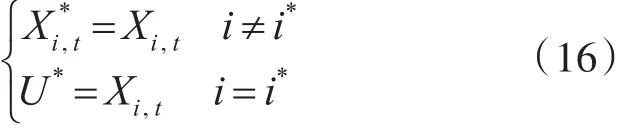
此时，其提议分布为

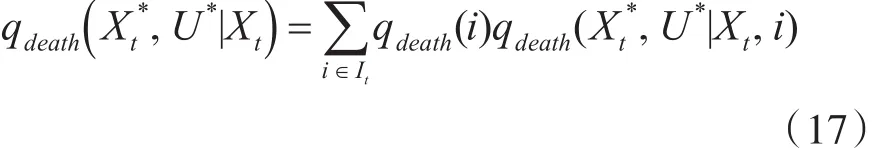
其中：qdeath(i)为选择的目标概率，i*为目标索引，其会加入到消失目标的集合Dt中，消失目标的提议分布定义为

此时，采样的接受率为

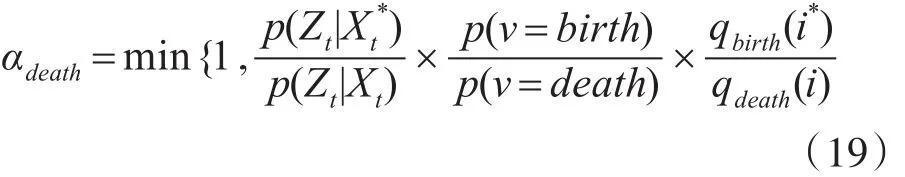
3）“更新”：即在保持其他目标状态不变的情况下，对当前选中目标的状态进行更新，而且其本身是可逆的，定义为：

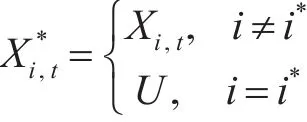
此时，其提议分布为

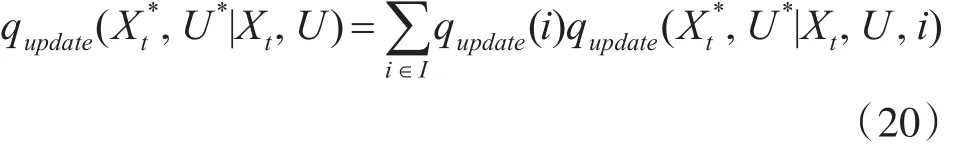
其中，qupdate(i)为选择更新目标的概率，且选择目标的提议分布定义为

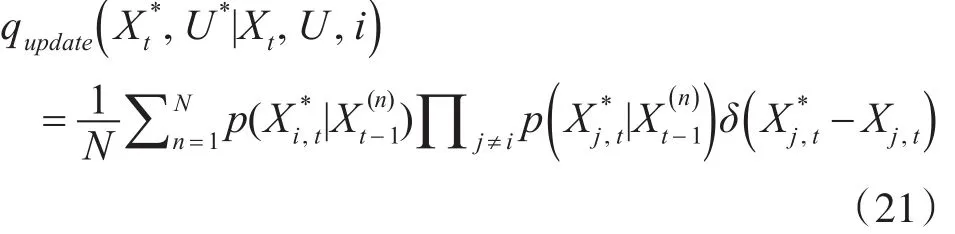
此时，采样的接受率为

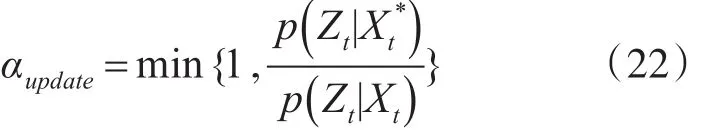
4 留箱体检测

在完成对可变多目标的检测追踪建模后，可以获得当前帧中箱体和人员的检测，及总体的目标数量、索引、类别、位置及范围的信息，进而可以依据箱体的移动速度及人员和箱体之间的交互关系判别箱体是否为遗留，主要包含箱体移动的判断及人员和箱体间关系的判断两部分。

箱体移动的判断部分，采用差帧的方式进行判断，定义为

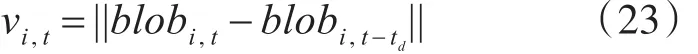
其中，td为超前当前时刻d帧，blobi，t为目标i的中心位置，当速度基本处于零附近，则认为箱体没有移动。

箱体遗留判断部分，当检测箱体移动速度为零后，需要结合箱体的活动周期，来进一步确定是否为遗留，具体结合3部分中转换类型中的“新生”来进行判断，即当箱体被遗留前，人员和箱体之间应该是融为一体的，表现为跟踪过程中的同一状态，而当箱体被遗留后，箱体和人员应拆分为两个目标，表现为跟踪过程中出现新的人员或箱体。

整体算法流程如下：

算法初始化：

RJMCMC采样：

依据v～p(v)选取一种转换类型，其中类型包括“新生”、“消失”和“更新”；

依据qv(i)从选取的转换类型中选取目标i*；

依据提议概率从选择的转换类型中对目标i*采样状态，具体如下：

基于选择转换类型计算接受率αv（“新生”采用式（15），“消失”采用式（19），“更新”采用式（22））；

结合式（10）的似然概率及采样样本计算状态的后验估计；

结合式（22）及对应人员和箱体间的“新生”转换，判断箱体是否遗留。

5 实验结果及分析

采用PETS2006数据源进行算法性能的验证，原数据源中提供多摄像头的序列，在实际实验中只使用其中一个视角进行测试，由于RJMCMC的随机性，对每个序列数据进行7次建模，并取均值作为计算结果。

对序列S1，S2，S3，S4，S5，S6，S7视频序列进行箱体遗留物检测，检测结果如图2所示。

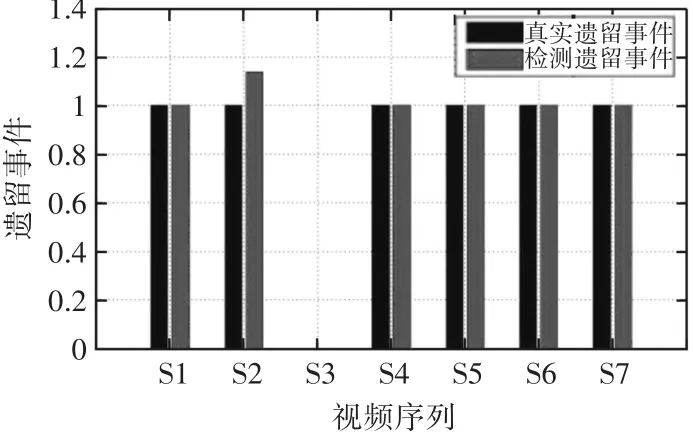
图2 箱体遗留检测

其中，深色表示真实遗留箱体的事件数，浅色为检测的遗留箱体的事件数，从中可以看出，除了S4，所提模型成功地检测出了箱体遗留事件，在序列S2中出现误报的情况，而对于S3没有事件发生的情况，也可以进行处理，对于序列S4，在该序列中箱体的所有者坐在了箱体上，同时出现了另外一个人距离形体很近，而箱体所有者又离开，在这种情况下，模型错误地检测箱体和人员没有分开。

图3为S5中遗留物检测结果，检测出的目标使用不同的轮廓进行标记，当检测到遗留箱体时，高亮显示箱体。

通过基于跟踪率和检测率的方法并对比BPF算法［18］对本文所提算法进行性能分析，如图4所示。BPH算法采用粒子滤波算法分别和GMM检测法、Adaboost算法相结合的方法进行测试，其中箱体识别部分结合检测物的大小和区域特征来实现。

图3 S5中遗留物检测结果

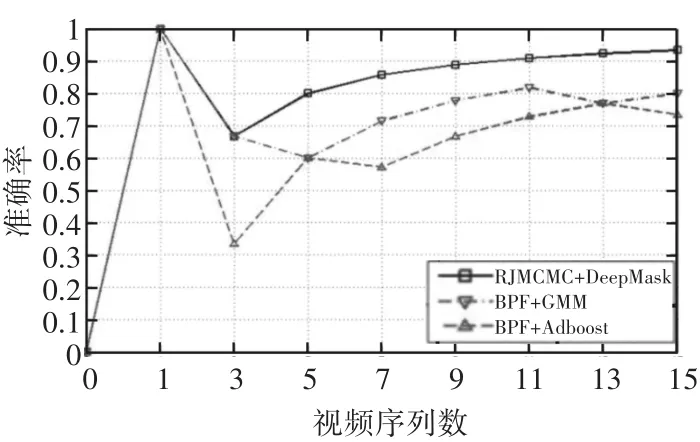
图4 召回率

6 结语

本文基于深度神经网络和RJMCMC提出了一种遗留箱体检测方法，将跟踪、分割和检测融入到贝叶斯推理框架下，其中分割和检测部分采用深度神经网络Deepmask实现，并用来计算模型的似然概率，模型求解部分采用RJMCMC抽样实现后验概率的进行估计，然后，结合箱体的移动速度及人员和箱体的交互关系来判定是否出现遗留箱体，定量结果表明本算法具有较好的性能。实验中RJMCMC求解部分较为耗时，下步工作采用神经网络来近似求解状态的后验概率，以改进检测速度。