优化初始聚类中心及确定K值的K-means算法

蒋 丽 薛善良

（南京航空航天大学计算机科学与技术学院 南京 211106）

1 引言

数据挖掘可以从大量有关数据中挖掘出隐含的、先前未知的、对企业决策有潜在价值的知识和规则。聚类是数据分析中的一项重要技术，在许多领域都得到了广泛应用［1］，包括机器学习、模式识别、图像分析等。到目前为止，已经提出了许多经典的聚类算法，比如基于划分的K-means算法［2］、基于密度的DBSCAN算法［3］、基于层次的CURE算法［4］、基于网格的 STNG 算法［5］等。本文主要研究基于划分的K-means聚类算法，由于它具有算法简单且收敛速度快的优点，所以得到较普遍的应用，但由于该算法中K个聚类中心是随机选取的，而实际数据集中可能存在孤立点和边界点，我们如果把孤立点和边界点作为初始聚类中心，就会影响聚类结果。为解决这个问题，本文结合基于密度的思想，首先将数据集按密度划分为核心点、边界点和孤立点，删除数据集中的孤立点和边界点并取核心点的中心点作为初始聚类中心再进行K-means聚类算法。改进后的K-means聚类算法聚类效果更好，聚类准确性更高。

2 K-means聚类算法思想及基本步骤

2.1 K-means聚类算法思想

1967年，MacQueen提出了K-means算法。K-means算法是一种基于划分的经典聚类算法。该算法最初随机选择K个数据样本作为初始聚类中心，在每次的迭代过程中，根据计算相似度将每个数据样本分配到最近的簇中，然后，重新计算簇的中心，也就是每个簇中所有数据的平均值。该算法结束的条件为聚类准则函数达到最优即收敛，从而使生成的每个聚类内紧凑，类间独立［6］。

2.2 K-means聚类算法基本步骤

input：包含n个数据对象的数据集合D以及聚类簇的个数K。

output：满足聚类准则函数收敛的k个聚类簇的集合。

K-means算法的具体步骤：

1）从数据集合D中随机选择K个数据对象作为初始聚类中心 Cj，j=1，2，3，…，k。

2）求出每个数据对象与初始聚类中心的距离D(Xi，Cj)，i=1，2，3，…，n，j=1，2，3，…，k。

3）根据求出的距离，将每个数据对象划分到最相似的簇中即若满足 D(Xi，Cj)=min{D(Xi，Cj)，j=1，2，3，…，n｝，则 Xi∈Yj。

6）判断：如果E≤ε，表示算法结束，否则，返回第2）步继续执行。

2.3 K-means聚类算法基本定义

1）样本xi和xj之间的想异度通常用它们之间的距离d(xi，xj)来表示，距离越小，样本 xi和 xj越相似；距离越大，样本xi和xj越不相似。距离一般使用欧式距离，欧式距离公式如下：

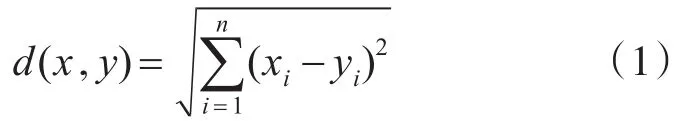
2）簇中心指一个簇中所有对象组成的几何中心点，簇的平均值在K-means算法中也称为簇中心，簇中心的公式如下：

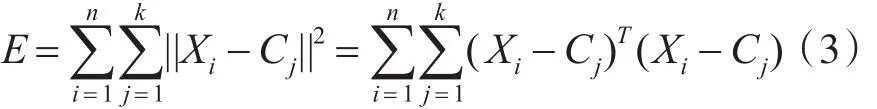
其中，Xi是数据集D中的每个数据对象，Cj是k个初始聚类中心。

4）聚类准则函数收敛，则聚类操作结束。给定一个阈值ε，假设ε足够小，在聚类过程中，当

其中n是簇 j的样本数目，Cj是指簇 j的中心［7］。

3）聚类准则函数（SSE（sum of the squared error））

K-means聚类算法使用聚类准则函数来评价聚类性能的好坏。聚类准则函数公式为：成立时，则聚类函数收敛。

3 K-means算法的优缺点

3.1 K-means算法的优点

K-means算法是数据挖掘中最常用的聚类算法之一，在文本挖掘中应用也较为普遍，具有以下优点：

1）K-means聚类算法简单、快捷、易行；

2）当面对大数据集时，K-means算法是相对可伸缩的并且是高效的，它的复杂度是O（n*k*t），其中，n是所有对象的数量，k是簇的数目，t是迭代的次数。

3.2 K-means算法的缺点

1）K-means算法中必须事先给出k即要生成的簇的数目，K值的选定非常难以估计。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适，对于不同的初始值，结果也可能不同。

2）在K-means算法中，首先要随机产生K个聚类中心，初始聚类中心的选择对聚类结果有较大的影响，一旦选择到孤立点，可能无法得到有效的聚类结果。如图1，图（a）是实际的数据分布，图（b）是选取了好的初始聚类中心得到的结果；图（c）是选取不好的初始聚类中心得到的结果，从图中可以看出，初始聚类中心的选取是至关重要的［9］。

3）K-means算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此，当数据量非常大时，算法的时间开销是非常大的。

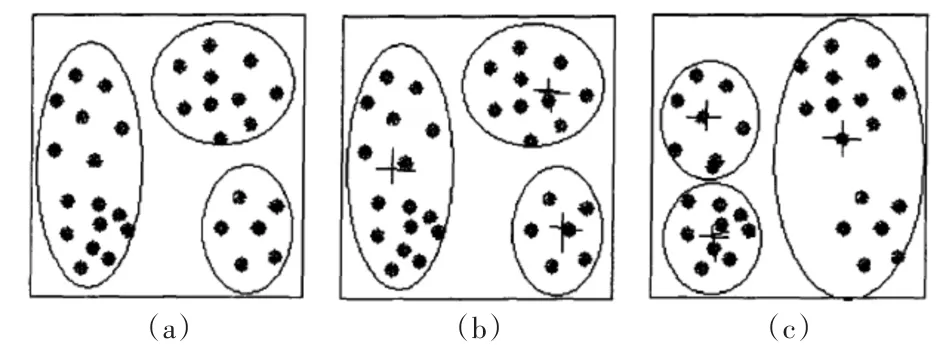
图1 基于K-means算法的一组对象的聚类

4 K值的确定以及基于密度选取初始聚类中心

Kmeans算法中，聚类数K值是用户输入，如果K值选取的不对，将影响聚类的结果，本文提出了基于类簇指标来选取K值的方法，类簇指标如类簇的平均半径或直径，经过选取不同的K值进行实验对比观察类簇指标，我们可以将上升或下降趋势很明显的类簇指标作为我们要选取的K值。图3是不同聚类数的聚类效果，图4是类簇指标的变化曲线。

考虑到K-means算法对孤立点的敏感性，本文提出了一种改进的K-means聚类算法，采用基于密度的思想，通过设定ε（半径）和MinPts（最小邻域点数）将数据样本划分为核心点、边界点和孤立点，排除孤立点和边界点后，取簇中核心点的中心作为新的聚类中心，最后再进行K-means聚类算法，实验表明，基于密度的K-means算法聚类效果更好。下面介绍基于密度思想的几个概念。

1）密度参数：以空间某点为中心，以半径ε做多维超球体，在球体内所包含的对象个数称为中心对象点的密度。个数越多，说明对象所处的区域数据密度越高；反之，说明数据对象所处的数据密度越低。

2）ε邻域：给定对象半径的ε内的邻域称为该对象的ε邻域，我们用Nε(p)表示点 p的ε半径内的点的集合，即 Nε(p)={q|q∈D，D(p，q)≤ε}，其中，D(p，q)表示 p对象和q对象之间的距离，一般使用式（1）来计算［10］。

3）MinPts：给定点在ε邻域内成为核心对象的最小邻域点数。对于有限的数据集，MinPts一般可用如下公式进行计算：MinPts=integer（m/25）［11］，m为数据集中数据总个数，如果数据集中数据很多，MinPts的值一般确定为10～20之间。

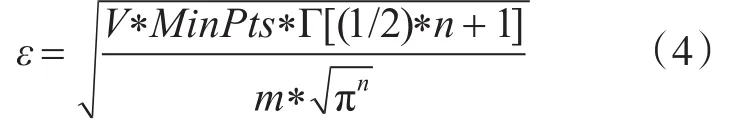
4）ε：用户输入的半径。我们假设数据集D是均匀分布，那么半径ε可利用如下公式［12］进行计算：其中，V是数据集D的容积，V利用如下公式计中对象的数量，n代表数据集的维度数量，Γ代表伽马函数。

5）核心对象、边界对象和孤立对象：给定ε及MinPts，若在半径ε内含有超过MinPts数目的点，则该对象为核心对象；边界对象为在半径ε内点的数量小于MinPts，但在ε领域之内至少有一个是核心对象；既不是核心对象也不是边界对象称为孤立对象。

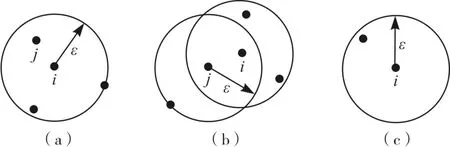
图2 半径为ε，MinPts为3的各对象密度

如图2所示，在半径为ε，MinPts为3的情况下，图（a）中的i对象就是核心对象，图（b）中的j对象为边界对象，图（c）中的i对象为孤立对象。

改进后的K-means聚类算法流程如下：

input：包含n个数据对象的数据集合D，最小邻域点数MinPts。

output：排除孤立点和边界点的聚类结果。

1）根据数据集D合输入的最小邻域点数MinPts计算出ε。

2）利用式（1）计算出数据集中每个点之间的距离，存储在相异度矩阵dis中。

3）从dis中取出第一个点到其它所有点的距离 dis（1，：），找到在 ε范围内所有的点 find（（dis（1，：）＜= ε），根据其数量length（find（（dis（1，：）＜=ε））区分点的类型并进行处理从而将数据集中每个数据点划分为核心点，边界点和孤立点，然后将孤立点和边界点从数据集中删除。数据集D中数据对象个数为N，假设边界点个数为Nb，孤立点个数为No，那么经过处理后的数据集D中数据对象的个数为（N-Nb-No）即剩余核心点的个数。

4）扫描所有核心点，取每个簇中核心点的中心作为K-means聚类算法的聚类中心；

5）进行传统的K-means聚类算法。

附：相异度矩阵dis。

其中，d(i，j)代表对象i和j之间的相异度，值越小，说明相似性越高，反之，相似性越低。

5 仿真实验分析

为了检验改进算法的有效性，对原始算法和改进算法进行了对比实验，用于实验的CPU是Intel（R）Core（TM）i5-3210M CPU@2.50Ghz，内 存 为4GB，实验软件环境：操作系统为64位win7，编程软件用MatlabR2010b。

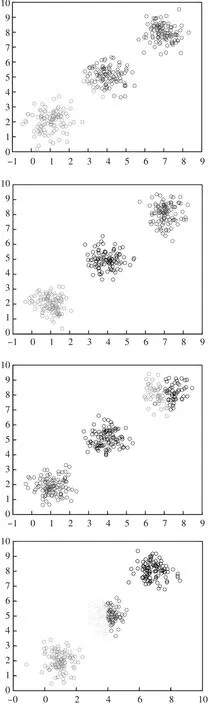
图3 不同聚类数目的聚类结果

图4 类簇指标的变化曲线

图3中的数据是用三个二元正态高斯分布生成，输入不同的聚类数目k=2，3，4，5，得到不同的聚类结果，从图中可以看到K=3时，聚类效果最好。图4分别是不同的聚类数目的类簇指标，从图中可以明显看到，当k=3时，类簇指标发生明显的变化趋势，所以K的正确取值应该为3。

表1 传统K-means与改进的K-means聚类算法的准确率

观察图5和图6会发现，数据集相同的情况下，传统的K-means聚类算法没有排除孤立点和边界点，准确率只有70%，聚类质量不优，聚类结果将没有多大的参考意义，改进后的K-means聚类算法排除了孤立点和边界点，准确率达到98%，聚类结果更具有参考价值。

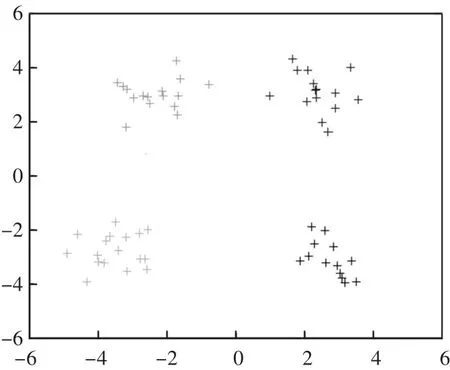
图5 传统K-means算法聚类结果图

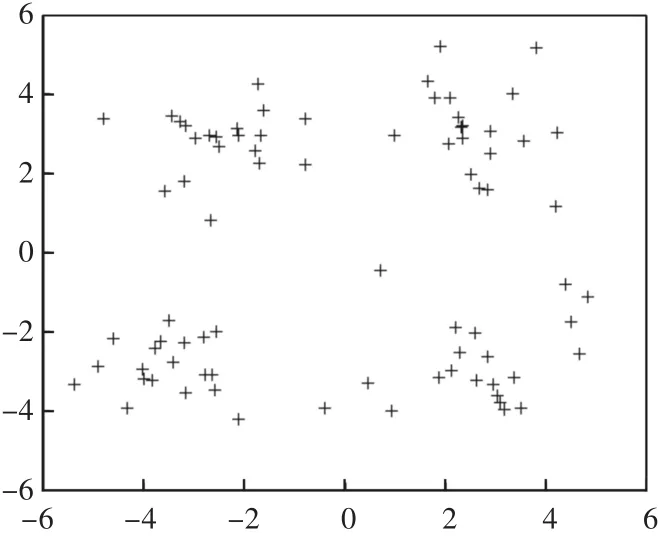
图6 改进的K-means算法聚类结果图

6 结语

K-means聚类算法是一种被广泛应用的算法，但初始聚类中心是随机确定的，实际数据集中存在孤立点，当簇中存在孤立点和边界点就会严重影响簇的中心点的位置，影响聚类结果的准确性和聚类的质量。本文改进了初始聚类中心的随机选取，将基于密度的思想引入到K-means算法中，避免了随机选取到孤立点和边界点的情况，实验表明该算法具有良好的性能，但还需要做进一步的研究：当数据量增大时，算法的运行时间也随之增大，如何节省算法的运行时间是下一步要研究的内容。