基于MOM的正弦复合粗糙表面光散射特性研究

闫克丁 付永升 于小宁 杨建华

（西安工业大学电子信息工程学院 西安 710032）

1 引言

激光雷达因其波长短，单色性好，目标分辨能力和抗干扰能力强，使激光雷达在军事和民用领域有广泛的应用［1］。激光雷达研制过程中，雷达目标散射特性研究为雷达系统提供目标的光谱和图像特征及其数学模型等数据。因此为了提高激光雷达目标识别能力，必须深入研究目标的表面光散射特性，建立目标的散射特性数学模型，对在复杂背景和各种干扰下提高目标探测能力具有重要意义［2］。目前所研究的粗糙表面大多为非确定性表面，而针对确定性和非确定性表面组合而成的复合粗糙表面光散射研究还不多见，然而真实环境中的很多表面是周期表面与随机表面叠加构成的复合随机表面，因此对复合随机表面进行光散射研究有重要意义。

目前国内外有关粗糙面散射研究的主要方法有解析方法和数值方法两大类［3～6］。解析方法中最广泛应用的是基尔霍夫近似法，1963年Beckmann首次引入基尔霍夫近似来处理散射场的边界问题，采用数理统计方法计算了积分形式的散射场，随后又引入遮蔽函数，基本解决了大入射角和散射角下的散射问题［7］。基尔霍夫近似方法比较简单，在工程当中得到了广泛应用。随着计算机的飞速发展，数值方法应用得越来越广泛，其中应用最广泛的是有限元方法和矩量法［8］。有限元法将所要求解的边值问题转化为变分问题，再离散化后变成普通多元函数的极值问题，最后通过求解代数方程组得到所求边值问题的数值解；MOM（矩量法）将电场或磁场积分方程中未知量展开，用权函数对积分方程两边作内积，从而把积分方程转化为代数方程进行求解。在这些方法中，矩量法因其计算准确度较高，物理意义明确而得到比较广泛的应用。

本文利用线性滤波法生成两组具有正弦复合随机粗糙表面，采用基于MOM的蒙特卡罗方法分别对这两组表面在s偏振光入射时的散射光强度空间分布进行了数值计算，并分析了散射强度分布特征。

2 基于MOM的蒙特卡罗光散射计算方法

2.1 复合随机粗糙面生成

一般可认为随机粗糙表面高度可由许多不同频率的谐波叠加而成［9］，因此可采用线性滤波法来生成随机粗糙面：先在频域谱进行滤波，然后进行逆傅里叶变换得到粗糙面高度，来生成模拟随机粗糙面模型，各个谐波的振幅可采用蒙特卡罗方法由独立的Gauss随机变量来表示。根据以上分析，长度为L的一维粗糙面模型可表示为

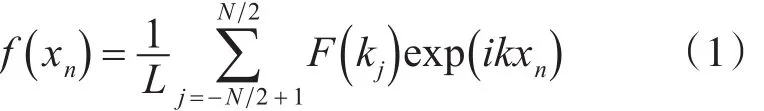
其中，xn=nΔx(n =-N 2+1，…，N 2 )是第 n个采样点，F(kj)为f(xn)的Fourier变换，可表示为

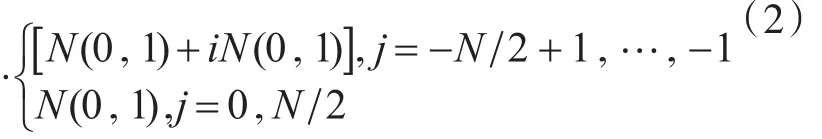
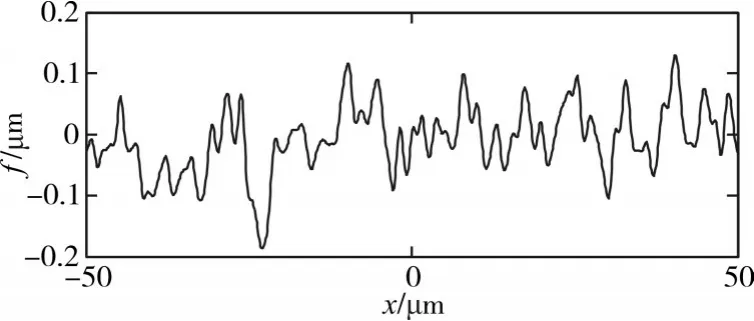
图1 一维Gauss随机粗糙面模型

根据Wold［10］的分解理论，任何一个离散的静态过程都可表示为2个完全不相关过程的和，其中一个为确定性过程，一个为非确定性过程。张移山［11］也证实工程中许多表面成双高斯分布或多高斯分布。基于此理论，可以通过分离表面的确定和随机成分来模拟复合表面。本文在模拟过程中的确定成分是正弦分量，如图2和图3所示为正弦复合粗糙表面。

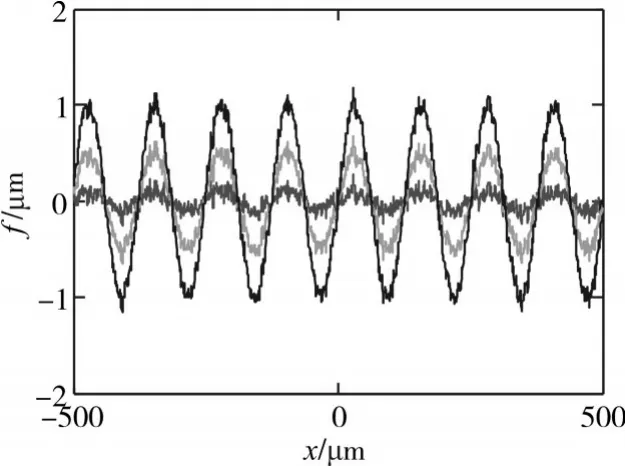
图2 相同周期不同振幅的正弦复合粗糙表面

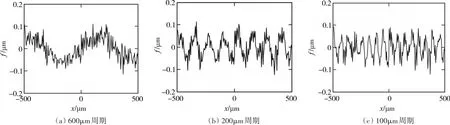
图3 相同振幅不同周期的正弦复合粗糙表面

图2中有三个正弦复合粗糙表面，它们具有相同的起伏周期为125μm，但是振幅不相同，分别为1μm，0.5μm，0.1μm。

图3中（a）（b）（c）三个图中正弦复合表面的振幅相同为0.1μm，但是周期不同，分别为600μm，200μm，100μm。

2.2 一维锥形入射波

粗糙面光散射仿真算法只能处理有限表面，同时为了防止平面波入射时在两个端点出现人为反射现象，一般将入射波取为锥形波，具备高斯特性，在两个边界入射时光强趋于零，避免了表面电流的突变。锥形入射波函数为

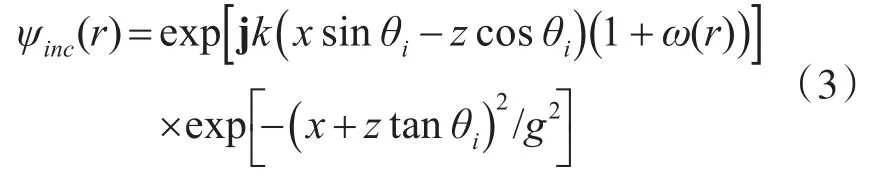
其中g为锥形参数，一般取L 10到L 4之间，它决定入射波的入射宽度和粗糙面长度取值。

入射光矢量为

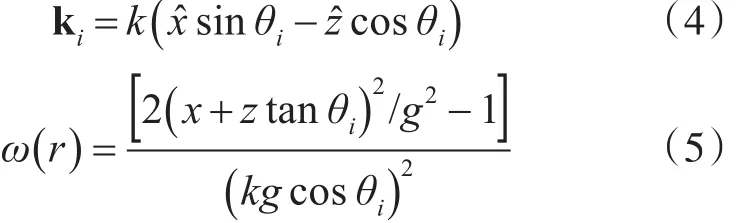
锥形波入射功率为

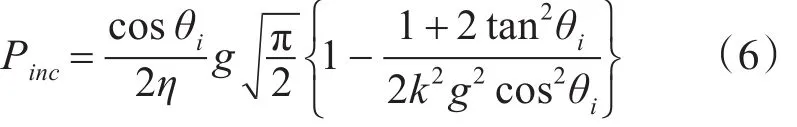
2.3 表面积分方程

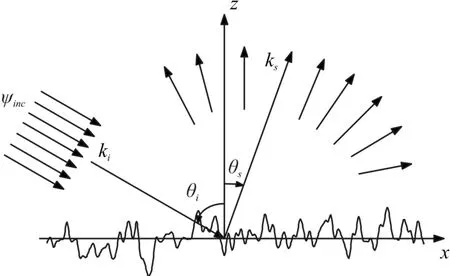
图4 一维粗糙面散射几何模型

图4为入射光入射到一维随机表面上几何模型，空间总场应等于入射场和散射场之和，即ψ(r)=ψinc(r)+ψs(r)，ψ(r)满足：

利用格林函数可得：

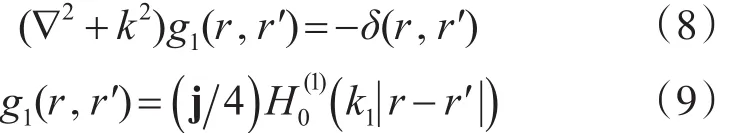
应用格林第二恒等式，化简可得到

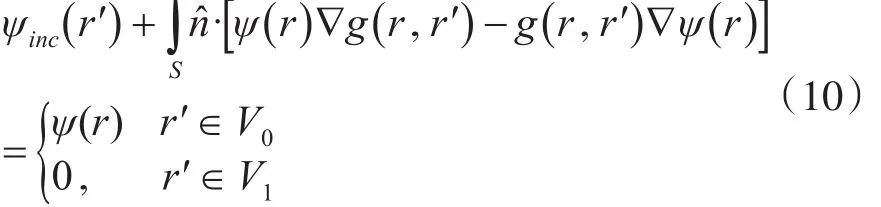
r在粗糙表面，r′在粗糙面上。

根据狄利克莱和诺依曼边界条件化简式（10），采用点配法转化成矩阵方程，使用Bi-CGSTAB迭代算法求解矩阵方程，带回原来积分方程最终得到散射场。

2.4MOM的蒙特卡罗模拟

基于MOM的蒙特卡罗粗糙表面散射场计算方法分为3步：

1）利用线性滤波法生成许多数字随机粗糙表面，这些表面起伏各不相同，但是具有相同的统计性质如均方根高度和相关长度；

2）利用MOM方法计算每个随机粗糙表面的散射场；

3）计算平均散射场即可认为是该粗糙度参数下的散射场。

3 金表面光散射场数值计算与分析

3.1 随机粗糙表面光散射计算

选用入射波长为激光探测常用的λ=0.6328μm，以金表面为例进行数值计算，这些表面相关长度相同为T=2μm，均方根高度从 δ=0.01μm到 δ=1.2μm不等，计算s偏振光在30°角入射到该组表面的散射光强度空间分布，金在该波长下的折射率为n=0.167+3.149i。数值计算时生成3000个随机粗糙面样本，每个样本长度为100λ，采样点数为N=1000。随机粗糙表面光散射数值计算结果如图5所示。

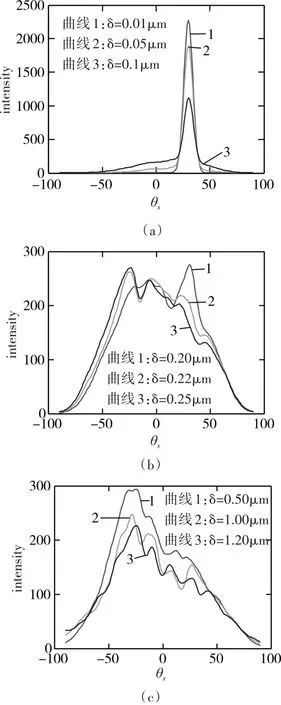
图5 无正弦起伏表面光散射强度分布

从图5（a）中可以看出：三个表面的散射是典型微粗糙面的镜反射，其中样本1的散射光有尖锐的镜向峰值，峰值两侧强度下降迅速，随均方根高度的增加，峰值逐渐减少和强度分布逐渐展宽；从图5（b）中可以看出：三个表面的散射是典型弱粗糙面的散射，反射方向也存在峰值，但与镜反射峰值相比，强度小但宽度大。从图5（c）中可以看出：随着粗糙度的进一步增大，入射方向是强度明显减弱，说明多次散射的作用明显增强。

3.2 幅度相同周期不同的正弦复合表面光散射计算

选取一组幅度相同周期不同的复合表面进行蒙特卡罗光散射数值计算，其中粗糙面均方根高度为0.1μm，正弦起伏的振幅相同为1μm，周期不同，分别为600μm，200μm，100μm，其散射光强度空间分布如图6所示。

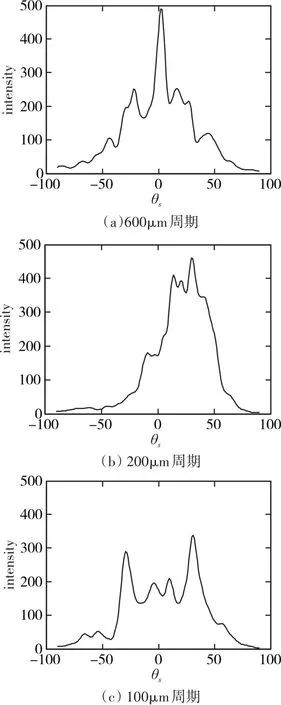
图6 不同周期的复合表面散射光强分布

图6中可以看出，三个复合表面的光散射强度分布不同，6（a）中表现为典型的镜面反射，6（b）中由于正弦周期变短，出现峰值下降，拓宽等散射特征；6（c）由于正弦周期进一步变短，峰值进一步降低，表现为典型漫散射特征。可以看出正弦复合粗糙表面的正弦周期对光散射特征的影响较大。

3.3 周期相同振幅不同的正弦复合表面光散射计算

选取一组幅度相同周期不同的复合表面进行蒙特卡罗光散射数值计算，具有相同的起伏周期为125μm，粗糙面均方根高度为0.1μm，但是正弦振幅不相同，分别为0.1μm，0.5μm，1μm，其散射光强度空间分布如图7所示。

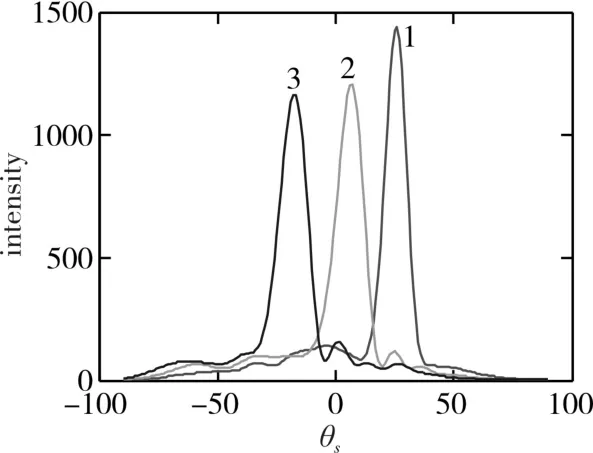
图7 不同振幅的正弦起伏表面散射光强分布

图6中可以看出，三个正弦振幅复合表面的光散射强度分布差距很大，由于复合表面1的正弦振幅和均方根高度都很小，可认为是微粗糙表面，表现为典型的镜反射；复合表面2的正弦振幅较大，可认为是弱粗糙表面，峰值向中心移动，表现为强度相对集中的漫反射；复合表面3的正弦振幅进一步增大，可认为是强粗糙表面，峰值进一步向左移动，表现为典型的后向散射特征。对比图7中三条曲线可以看出正弦幅度对复合表面的光散射特征的影响较大。

4 结语

采用基于MOM的蒙特卡罗方法研究了复合随机粗糙表面的光散射强度分布特征，首先用线性滤波法模拟生成两组相同周期不同振幅和相同振幅不同周期的正弦复合随机粗糙表面，数值计算了这两组复合表面散射光的空间强度分布。结果表明，正弦复合表面光散射特征与正弦周期和正弦振幅有关，随着正弦周期变小，散射特征从镜反射变到漫反射；随着正弦振幅的增大，散射特征从镜反射变成到漫反射再进一步变成后向散射。