基于灰色深层感知器的财政收入预测模型
于 辉
(西安邮电大学计算机学院 西安 710121)
1 引言
作为衡量政府财力的重要指标之一,财政收入预测一直都是专家学者们研究的热点[1~2]。目前常用的预测方法有回归分析法、时间序列分析法、灰色预测法和神经网络法等[3~4]。财政收入数据及其相关影响因素数据的变化往往具有随机性和非线性变化的特点,并且它们之间也具有非常复杂的非线性相关关系。目前,许多学者运用组合预测模型来进行预测研究。如范敏等运用灰色预测和常规BP(Back Propagation)神经网络组合模型对地方财政收入进行了预测,提高了预测准确度[5];方博等利用基于时间序列的ARMA模型与常规BP神经网络相结合,通过实验证明了组合预测模型比单一预测模型能够获得更准确的结果[6]。
不过以上研究运用的组合预测模型所使用的常规BP神经网络的BP算法存在收敛速度缓慢、学习精确度不高等缺陷。本文尝试使用基于深度学习思想的深层神经网络(Deep Neural Network,DNN),深层感知器(Deep Multi-layer Perceptron,DMLP)模型来解决常规BP神经网络的一些缺陷,同时综合灰色预测的优点,根据组合预测方法思想,建立基于灰色DMLP财政收入预测模型,并以西安市财政收入及其影响因素统计数据对组合模型进行检验,来论证所构建组合预测模型的预测准确度和实用性。
2DMLP模型构建及原理
2.1 DMLP的神经网络结构设计
依据 Delalleau和Bengio的观点[7],常规 BP神经网络之类的浅层网络,都使用不超过三层的结构,在解决真实世界的复杂应用问题时,往往出现表达能力不足的情况。在神经元数大致相同的情况下,深层网络通常比浅层网络函数表达力更强。不过精确预测隐含层所需要的神经元数量和神经网络所需要的层数,至今仍然存在理论上还没有解决的问题[8]。
由以上依据、实际经验和财政收入预测问题的特点,本文选用了DNN中的判别模型DMLP。如图1所示,DMLP采用四层网络结构,隐藏层H1和H2的神经元数量为输入层X的1.5~2倍左右,输入层X和输出层Y的神经元数量由具体问题来确定。
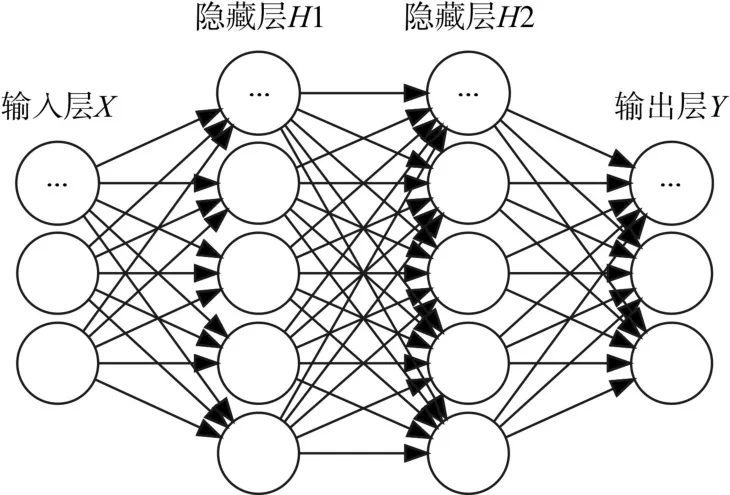
图1 四层DMLP神经网络
2.2 神经元激活函数的选取
神经元是神经网络操作的基本信息处理单位。一个神经元对输入信号 X=[x1,x2,…,xm]T的出加权求和的值,wi表示权重(模型参数),b表示偏差,f(·)表示激活函数。
2010年,Glorot和Bengio等提出在深度学习模型某些问题的应用中,使用简单、速度快的近似生物神经激活函数Softplus和ReLU替代常规的Sigmoid函数,在使用BP算法时可以提高训练速度,减轻梯度下降(Gradient Descent,GD)算法训练深层网络时的梯度消失问题[9]。
在图1当中隐藏层H1的神经元采用非线性的Softplus函数激活用来提高DMLP的解释表达能力,隐藏层H2的神经元采用线性的ReLU函数激活使得DMLP学习周期大大缩短,提高模型的综合学习速率和效率。Softplus、ReLU和Sigmoid的函数公式分别表示如下
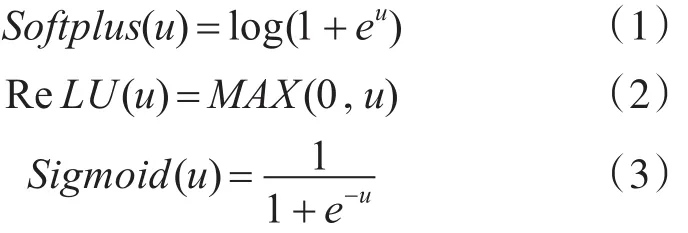
2.3 模型的学习训练方法
本模型用于预测问题,采用基于δ学习规则的BP算法,这是一种有指导的学习算法。与常规BP神经网络的BP算法略有不同,对目标函数取得最小值的权重和偏差的计算采用自适应矩估计(Adaptive Moment Estimation,Adam)算法[10]来替代常规的GD算法,克服其易陷入局部最小值的缺点。
根据图1,设输入层X与隐藏层H1的权重为WH1,偏差为bH1;隐藏层H1与隐藏层H2的权重为WH2,偏差为bH2;隐藏层H2与输出层Y的权重为WY,偏差为bY。
当正向传递时,各层神经元的输出满足如下公式:

当反向传播时,目标函数采用均方误差(Mean Squared Error,MSE),定义如下
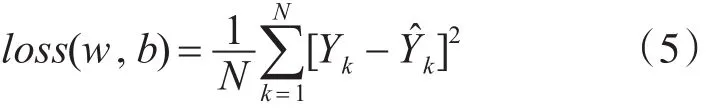
其中w为所有权重集合向量,b为所有偏差集合向量,N为训练样本的个数,Yk为第k个训练样本的期望值向量,Ŷk为第k个训练样本所预测的值向量。如果loss(w,b)接近于0,表示Yk接近输出预测值向量Ŷk,即学习效果很好。为找到满足要求的w和b,采用Adam算法。该算法利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam算法的优点主要在于经过偏差校正后,每一次迭代学习率都有一个确定范围,使得参数比较平稳。根据文献[9],该算法用于深度学习问题最好的参数默认值可设置为α=0.001,β1=0.9,β2=0.999,ε=10-8。 f(θ)为随机目标函数,与loss(w,b)相对应,θ为参数向量,与w和b相对应;gt为 f(θ)的一阶梯度;mt为一阶矩估计向量,初值为0;vt为二阶矩估计向量,初值为0;m̂t,v̂t是对 mt,vt的校正;t为时间步。当 θt收敛时,模型训练完成,学习结束。其算法流程如下所示。

3 灰色模型构建及检验
灰色模型GM(1,1)对小数据量数据预测通常表现出优良的性能,其建模过程[11]如下所示。
设变量 X(0)={X(0)(i),i=1,2,…,n} 为一非负单调原始数据序列,建立灰色预测模型:首先对X(0)进行一次累加得到一次累加序列X(1)={X(1)(t),t=1,2…n}。
对X(1)可建立下述一阶线性微分方程:

即GM(1,1)模型。
求解微分方程,得到预测模型如下
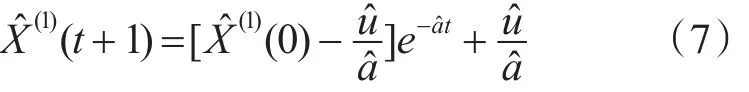
由于GM(1,1)模型得到的是一次累加量,将GM(1,1)模型所得数据 X̂(1)(t+1)经过累减还原为X̂(0)(t+1),即 X(0)的灰色预测模型如下
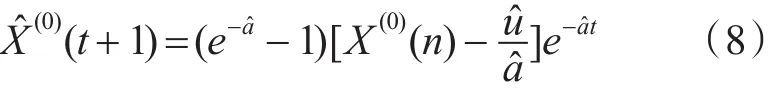
残差计算如下

灰色模型预测结果采用后验差检验法进行检验。设已按GM(1,1)建模法求出 X̂(0)和残差,原始序列X(0)及残差序列E的方差分别为和,则

计算其后验差比为C=S2/S1。计算其小误差概率为 p=P{ ||e(t)-eˉ<0.6745S1}。指标C越小越好,P越大越好。一般将模型精度等级分为四级,后验差检验模型精度表如表1所示。

表1 后验差检验判别参照表
4 灰色DMLP组合模型构建
设财政收入为Y,它的N个相关影响因素序列为(x1,x2,…,xn),且Y与这些因素表现为关系紧密的非线性相关关系。它们在T个连续的时期内连续观测值为 (x1,t,x2,t,…,xn,t;Yt),其中 t=1,2,…,T。所建立的组合预测模型旨在找出序列(x1,x2,…,xn)对Y的定量影响规律。基于 GM(1,1)和DMLP的组合预测模型对财政收入在T+1时期的值进行预测主要包括以下步骤。
步骤1:利用GM(1,1)模型,根据每个影响因素 xi,t(i=1,2,…,n)在1~T时期的观测值,即根据序 列 值 (xi,1,xi,2,…,xi,T) 预 测 出 其 在 T+1 时 期x̂i,T+1的值。则在T+1时期,所有与财政收入Y相关因素的预测值序列为 (x̂1,T+1,x̂2,T+1,…,x̂n,T+1)。
步骤2:以1~T时期的观测值序列 (x1,t,x2,t,…,xn,t;Yt)作为训练样本,其中Yt为作为监督训练的标签值,代入DMLP神经网络对模型进行训练。其中DMLP的输入层神经元个数为影响财政收入因素的个数N,输出层神经元个数为1。隐藏层H1、H2神经元个数为2N。
步骤3:用步骤1灰色模型GM(1,1)预测的值序列 (x̂1,T+1,x̂2,T+1,…,x̂n,T+1)作为输入样本代入训练好的DMLP预测模型当中,可以得到财政收入在T+1期的预测值 ŶT+1。
步骤4:组合模型预测效果评价采用均方根误差(Root Mean Squared Error,RMSE)和平均绝对百分误差(Mean Absolute Percentage Error,MAPE)指标来衡量。它们的定义如下
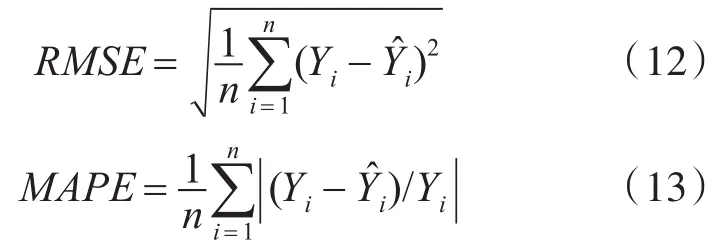
其中Yi表示第i个实际值。Ŷi表示第i个预测值。RMSE代表了预测值的离散程度,最佳拟合情况为RMSE=0。一般认为MAPE小于10%时,预测准确度较高。
5 组合模型预测验证实验
5.1 实验数据来源
本文针对财政收入预测问题,遵照科学可行性的原则,以西安市2004~2015年财政收入及其相关影响因素的统计数据作为检验样本来对所提出的组合预测模型进行验证分析,数据来源于西安统计年鉴2016版,详细数据如表2所示。在参考近年来西安市财政局的财政预决算报告、西安市统计局的国民经济和社会发展统计公报及相关经济学资料后,选取生产总值(X1,单位:亿元)、全社会固定资产投资总额(X2,单位:亿元)、社会消费品零售总额(X3,单位:亿元)、旅游总收入(X4,单位:亿元)和进出口总额(X5,单位:亿美元)共5个因素为自变量,作为影响西安市财政收入(Y)的主要因素。
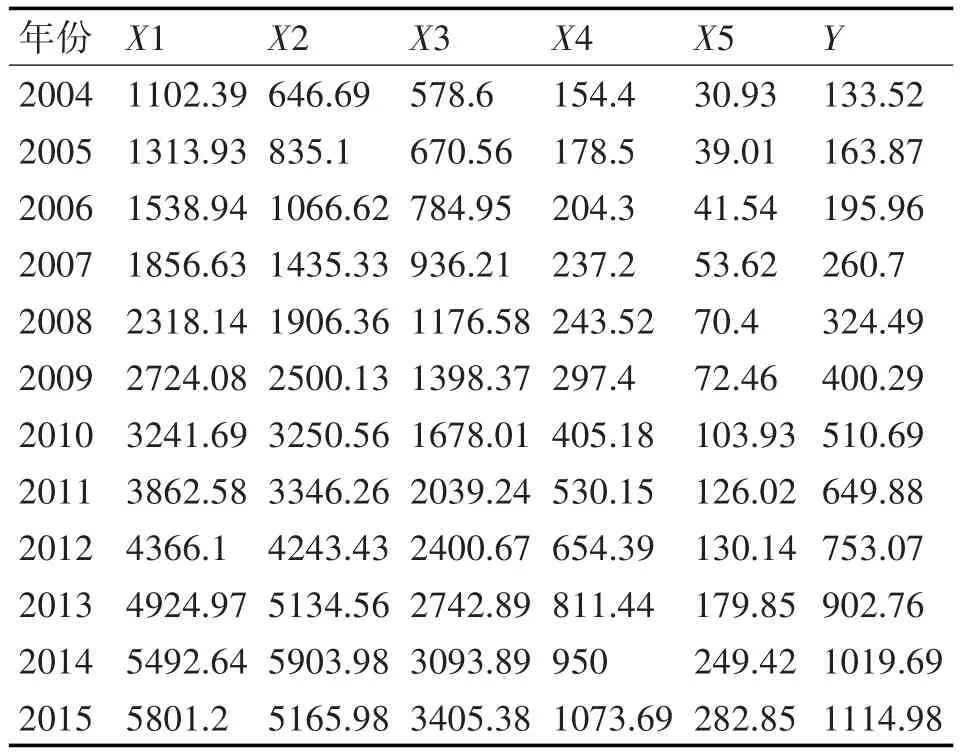
表2 西安市2004-2015财政收入相关统计数据
参照表2,以2004~2013年的数据作为训练集,2014~2015年的数据作为测试集,利用组合预测模型对西安市2014年和2015年的财政收入进行预测。
5.2 灰色模型预测验证分析过程
分别把X1~X5这5个财政收入影响因素在2004~2013年所对应的5对时间序列值代入到利用Python语言所写好的GM(1,1)模型当中,预测出2014年X1~X5的值。接着,结合2014年预测出的X1~X5的值,分别把X1~X5在2004-2014年所对应的5对时间序列值再次代入到GM(1,1)模型当中,预测出2015年X1~X5的值。最终预测结果及精度评价如表3所示。

表3 灰色预测结果及精度等级
从表3可以看出,2014~2015年西安市财政收入各个影响因素X1~X5预测精度较高,基本上都达到了“好”的等级。不过X2在2015年的预测值为“勉强合格”的等级,原因在于2015年以来,受“十二五”规划中大型项目完工、房地产市场整体调整回落、投资项目承接不足、民间投资意愿不强等多重因素影响,西安市固定资产投资总额10多年以来首次呈负增长。所以预测值与真实值稍有偏差,不过在可接受的范围内。
5.3 DMLP预测验证及对比实验分析过程
利用由Python编写基于TensorFlow的深度学习库Keras搭建四层DMLP(5-10-10-1)深层神经网络,结合灰色模型预测结果同常规BP神经网络做对比实验并进行验证分析。
四层DMLP的Keras配置参数分别为:输入层输入维数(input_dim)为5,输出维数(output_dim)为10;第一隐藏层激活函数(Activation)为softplus,input_dim为10,output_dim为10;第二隐藏层Activation为relu,input_dim为10,output_dim为10;输出层input_dim为10,output_dim为1;目标函数(loss)为mean_squared_error;梯度优化器(optimizers)为 Adam;模型训练迭代次数(nb_epoch)为1000。
作为对比试验的BP神经网络结构取5-10-1的网络结构。隐含层激活函数用Sigmoid激活,目标函数为MSE,梯度计算采用GD算法,模型训练迭代次数为1000。
根据表2,把2004~2013年X1~X5的值作为输入样本,Y作为与之相对应的标签值,分别代入四层DMLP模型和三层常规BP神经网络模型进行训练。训练效果如图2和图3所示。

图2 DMLP训练效果
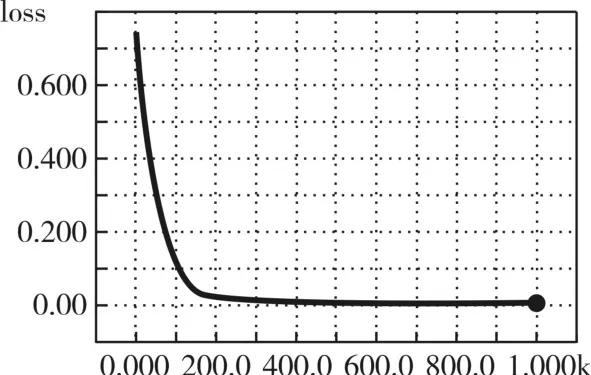
图3 BP神经网络训练效果
由图2可以看出,DMLP模型在训练迭代大约100次时,其模型loss值开始收敛。训练迭代1000次,训练完成,最后的loss值为0.00285。由图3可以看出,BP神经网络模型在训练迭代大约200次时,其模型loss值才开始收敛。训练迭代1000次,训练完成,最后的loss值为0.00589。对比图2和图3,在横轴取相同的训练迭代次数,观察纵轴loss的取值,可以发现DMLP的loss值总小于BP神经网络的loss值。对比这两种模型的训练效果,可以看出,DMLP模型学习精确度高,收敛速度快。
把5.2中通过灰色模型预测的2014~2015年X1~X5的值代入到已经训练好的DMLP和BP神经网络当中,对2014~2015年的西安市财政收入的值进行预测。预测结果及组合模型预测效果评价如表4和表5所示。

表4 两种组合预测模型预测值与真实值比较

表5 两种组合预测模型预测效果评价对比
表4和表5的实验结果表明,本文所构建的灰色DMLP财政收入组合预测模型比基于常规BP神经网络的组合预测模型所预测的值更加接近于真实值,准确度高,具有推广性和实用性。
6 结语
本文结合深度学习思想与灰色预测模型,建立了基于灰色深层感知器的财政收入组合预测模型。灰色预测模型的使用增强了原始数据的规律性。通过与常规三层BP神经网络做对比实验,在四层DMLP模型隐藏层用Softplus和ReLU激活函数替代Sigmoid激活函数,在计算目标函数loss的最优参数时,使用Adam算法替代GD算法,提高了模型的学习精确度,加快了学习速率和收敛速度。DMLP四层网络结构和Softplus激活函数的使用增强了模型的解释能力和非线性拟合能力,提高了组合模型的预测准确度,使其预测结果更加接近于真实值,具有推广性和实用性。但是基于深度学习思想的神经网络模型在进行训练时,一些超参数的选择往往借助于经验,没有成熟的理论作支持,需要不断实验尝试。因此,还需要对深度学习理论做进一步的研究和学习,以便对所构建的组合模型做进一步的改进和优化。

