复杂装备精密产品Grey-PCE多质量特性稳健优化设计

万良琪, 陈洪转, 欧阳林寒, 张 笛, 李亚平

(1. 南京航空航天大学经济与管理学院, 江苏 南京 211106; 2. 南京林业大学经济与管理学院, 江苏 南京 210037)

0 引 言

柔顺复杂装备精密产品是一种以新型柔顺机构为重要组成部分的高技术密集型产品,广泛应用于武器系统、航空航天、微机电系统、生物医学等高尖端领域[1-2]。在实际复杂工况背景下,由于柔顺复杂装备精密产品多个质量特性稳健可靠性往往受到来自内部可控因子与外部噪声因子的双重不确定性影响,造成柔顺复杂装备精密产品多质量特性波动工程难题。根据工程实践可知,可控因子结构参数加工容差扰动而产生的不确定性是影响产品多质量特性的关键因素。因此,迫切开展不确定性结构参数情形下的柔顺复杂装备精密产品多质量特性稳健优化设计相关研究工作是保障高尖端领域这类产品稳健可靠运行的前提。

复杂装备产品多质量特性稳健优化设计是通过早期设计阶段消解多质量特性冲突来降低下产品质量波动的有效手段。因此,从源头上提高产品设计质量来增强产品质量特性的抗干扰性,其有效性已在航空航天、车辆工程等复杂装备领域得到广泛的应用验证。现有相关复杂装备研究主要体现在多目标稳健优化设计、多目标可靠性优化及结构可靠设计。文献[3-4]对于汽车车身与汽车发动机悬置系统采用了多目标稳健优化设计,解决了传统单目标优化的局限性和多目标冲突权衡问题;文献[5]构建了一种多目标响应加权灰靶可靠性优化设计模型,有效地解决了复杂装备产品可靠性设计优化与算法难题;文献[6]针对支架多目标优化设计中的多目标潜在冲突难题,构建了基于Kriging代理模型的多目标优化模型,解决了多目标潜在冲突问题;文献[7]基于双重Krigng代理模型、Topsis方法与灰色关联方法相结合对卡车驾驶室疲劳寿命进行多目标稳健优化设计,取得了良好的效果;文献[8]建立了混合不确定性情形下的泡沫填充薄壁结构耐撞性多目标稳健优化设计,并验证了模型的有效性。总结归纳上述文献可知,在不确定性情形下的柔顺复杂装备精密产品多质量特性冲突稳健优化设计方面的文献报道还偏少。其根源在于刚柔混合背景下的新型柔顺复杂装备精密产品多质量特性之间的相互矛盾、相互冲突相比传统刚性机构复杂装备更为复杂;同时,各质量特性与设计变量之间的非线性隐式关系相比传统刚性机构的复杂装备产品更加难于通过现有理论推导获取。代理模型往往是解决这一难题的有效途径。但在构建代理模型过程中需要进行大量模拟仿真获取多质量特性响应值;同时,在多质量特性冲突下的稳健优化设计模型中还需要考虑设计变量的不确定性分析,更增加了柔顺复杂装备精密产品多质量特性冲突工程难题的复杂性。

构建RBF[9-10]径向基模型、SVR[11]支持向量机模型、Kriging[12-13]模型与RSM[14]响应曲面模型是处理多质量特性与设计变量之间非线性隐式关系,同时降低优化过程中大量数值模拟计算难题,是实现多质量特性冲突下稳健优化设计的有效途径。根据文献[15-17]可知,Kriging模型、RBF径向基函数模型与SVR支持向量机回归模型能够较好地处理输入与输出之间高维、非线性等工程问题,然而,RSM响应曲面模型却不适用于高维、高度非线性情况;文献[18]从试验样本和预测精度角度,分析对比了Kriging模型、RBF模型、SVR模型和RSM模型,其指出了在试验样本较小情形下,RBF模型预测精度高于其他模型,SVR模型的预测结果相对更稳健,Kriging模型在应用过程中,难于判断其基函数系数取值大小对不确定性设计变量的影响程度。

根据上述现有代理模型的文献分析和柔顺复杂装备精密产品的分析可知,现有代理模型针对随机不确定性情形下的柔顺复杂装备产品适用性并不强。然而,关于多项式混沌扩展(polynomial chaos expansion, PCE)代理模型在处理随机不确定性建模方面,则具有一定的优势[19]。由于柔顺复杂装备精密产品多质量特性与随机不确定性结构参数之间存在非线性隐式关系,且微纳机构多质量特性对随机不确定性结构参数数据较为敏感;另一方面现有针对柔顺复杂装备精密产品多质量特性冲突权衡的报道还尚少。据此,本文提出一种不确定性设计变量情形下的柔顺复杂装备精密产品Grey-PCE多质量特性稳健优化设计新方法。将PCE代理模型和接近度灰色关联分析引入稳健优化设计方法中,以解决多质量特性波动及冲突的工程难题。本文方法与现有代理模型稳健优化设计方法相比,该方法具有良好的处理不确定性能力、消解多质量特性冲突能力与稳健抗干扰能力。

1 柔顺复杂装备精密产品多质量特性波动分析

柔顺复杂装备精密产品作为一种依靠新型柔顺机构自身的弹性形变来转换与传递运动及能量的技术密集型机械产品[20]。该产品在国防、医疗与航空航天等尖端领域有着广泛的应用基础。其主要作用:一是通过柔性形变来实现微位移的放大功能;二是通过固有频率实现其自身的快速响应功能。如图1所示,柔顺复杂装备精密产品放大机构工作原理,其通过压电陶瓷驱动器在机构内侧两输入端施加输入位移载荷,来实现放大机构外侧输出端产生输出微位移。

图1 柔顺复杂装备精密产品结构受力示意图Fig.1 Sophisticated equipment products of compliant mechanism structural force diagram

鉴于柔顺复杂装备精密产品放大机构的结构对称性,因此,对其四分之一的机构来研究其放大特性原理。当压电陶瓷驱动器对机构作用,产生一个水平方向上的输入位移载荷Δx时,其垂直方向会相应产生一对输出微位移Δy,此时,柔性杆CB的倾斜角度从α减小到α′,其机构运动如图2所示。

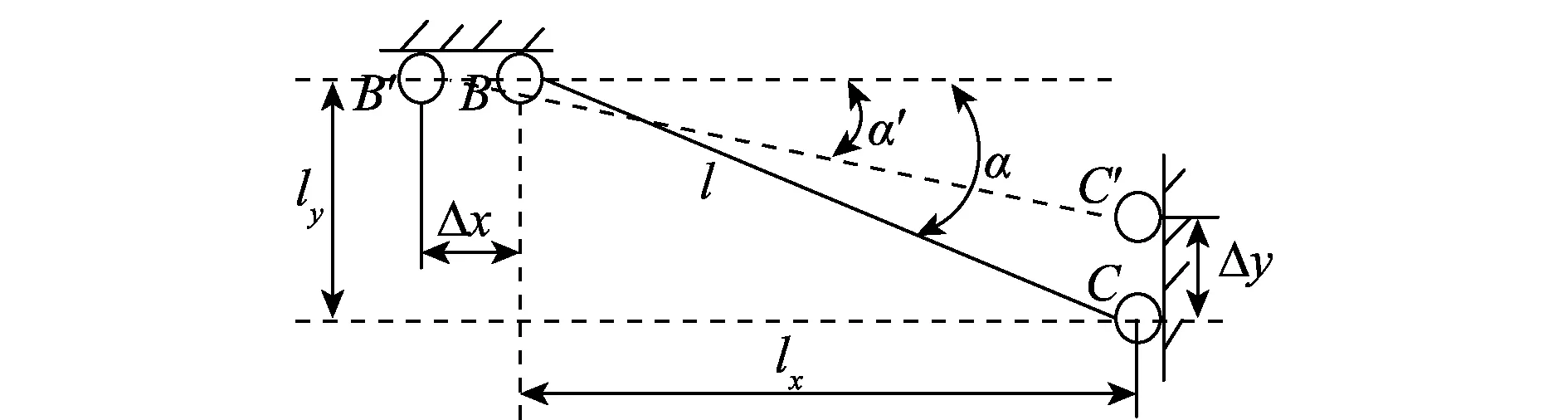
图2 柔顺复杂装备精密产品结构运动示意图Fig.2 Sophisticated equipment products of compliant mechanism structural movement diagram

根据上述柔顺复杂装备精密产品放大机构的运动位移关系分析可得到

(1)

式中,C′点到B′点的垂直距离为y2;C点到B点的水平距离为lx;C点到B点的垂直距离为y1;柔顺杆件CB的距离长度为l。

令x=0得到

(2)

根据式(1)、式(2)可推导出柔顺复杂装备精密产品放大倍数关系式为

(3)

由于柔顺复杂装备精密产品在实际复杂工况下,受到加工误差、外界载荷、疲劳退化等因素的影响,其结构参数稍有波动,可能导致放大倍数和固有频率两个质量特性产生显著性波动。进而影响其在国防科技、生物医学与航空航天等尖端领域功能稳健可靠运行。柔顺复杂装备精密产品稳健优化设计的目的不仅要使各质量特性的实际值尽可能达到目标期望值,而且还要降低产品质量特性波动。

随着实际工程问题越来越复杂,传统确定性优化设计现已难以获得柔顺复杂装备精密产品稳健可靠性设计方案。根据参考文献[21]，稳健优化设计与确定性优化对比如图3所示,当复杂装备精密产品受到外界不确定性影响情形下,设计变量(结构参数)x发生±Δx容差波动时,柔顺复杂装备精密产品多质量特性放大倍数和固有频率的确定性优化解①的波动幅度为Δf1(较大),然而稳健优化解②的波动幅度为Δf2(较小)。表明稳健优化解相比传统确定性优化解更具有较强的抗干扰能力。因此,柔顺复杂装备精密产品多质量特性(放大倍数和固有频率)稳健优化设计对实现产品功能稳健有着重要意义。

图3 稳健优化设计与确定性优化设计对比Fig.3 Comparison of robust optimization design and deterministicoptimization design

2 构建柔顺复杂装备精密产品多质量特性PCE代理模型

PCE代理模型是一种通过正交多项式的线性组合来有效描述和构建不确定性设计变量与目标响应之间关系的新型通用表达式[22-25]。由于刚柔混合背景下的柔顺复杂装备精密产品主要依靠柔性形变来传递运动与传统刚体运动不同,其传递运动过程更为复杂,通过理论推导来获得多质量特性和设计变量之间的函数关系往往难于实现。因此,本文采用PCE代理模型来解决多质量特性与设计变量之间的复杂非线性隐式函数关系这一难题。

根据上文不确定性结构参数情形下的柔顺复杂装备精密产品放大倍数与固有频率多质量特性波动分析,作出以下假设:

(1) 根据参考文献和工程实践可知,机械结构参数通常符合正态分布,据此本文假设柔顺复杂装备精密产品结构参数x=[x1,x2,…,xn]在设计空间内服从正态分布;

(2) 各结构参数x=[x1,x2,…,xn]之间相互独立。

根据多项式混沌扩展模型假设,同时,考虑柔顺复杂装备精密产品实际工程复杂度,进行不高于P阶的多项式混沌扩展进行截断,构建PCE代理模型如下:

(4)

在上述模型假设的基础上,本文构建和检验柔顺复杂装备精密产品多质量特性PCE代理模型主要步骤如下:

(1) 不确定性结构参数线性变换

描述柔顺复杂装备精密产品结构参数对多质量特性波动不确定性影响,可根据式(5)将结构参数x=[x1,x2,…,xn]转换为标准正态分布的不确定性设计变量。

(5)

式中,μxi表示结构参数xi均值;σ(xi)表示结构参数xi的标准差。

(2) PCE正交多项式基底选择

根据设计变量不同分布类型,其正交多项式基底也不同。本文依据PCE代理模型假设与结构参数服从正态分布,选择Hermite多项式作为PCE代理模型基底。在实际工程问题中,柔顺复杂装备精密产品往往存在多维不确定性结构参数影响。因此,多维Hermite多项式:

(6)

将多维Hermite多项式(6)代入PCE代理模型式(4),则柔顺复杂装备精密产品多质量特性PCE代理模型展开如下:

(7)

(3) PCE系数求解

通常,求解PCE系数主要有两类方法[25-27],即嵌入式方法和非嵌入式方法。嵌入式方法在PCE系数的计算过程中,需要对原始模型进行改进和调整,但这一过程增加了系数求解的复杂度;非嵌入式方法则不需要这一过程。据此,本文采用非嵌入式方法来求解PCE系数。

(4) PCE代理模型精度检验

(8)

3 基于多质量特性的Grey-PCE稳健优化设计

3.1 建立柔顺复杂装备精密产品多质量特性PCE稳健优化设计模型

柔顺复杂装备精密产品在早期设计阶段,由于忽略不确定性结构参数情形下的多质量特性之间相互冲突和矛盾,且多质量特性优化过程只考虑多质量特性的均值而未包括方差,而导致复杂装备精密产品多质量特性波动和冲突。据此,本文基于PCE代理模型和6σ稳健优化设计建模思路[28-29],构建柔顺复杂装备精密产品多质量特性PCE稳健优化设计模型:

(9)

式中,μfi为各质量特性的均值模型;σfi为各质量特性方差模型;s1i与s2i分别表示各质量特性均值和方差归一化系数;ω1i与ω2i分别表示各质量特性均值和方差权重系数。其中,柔顺复杂装备精密产品PCE稳健优化设计模型中各质量特性均值与方差模型估计如下:

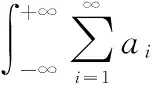
(10)

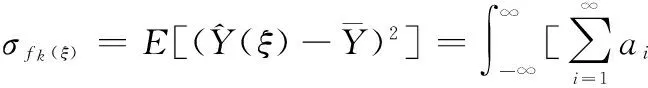
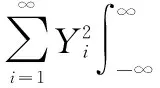
(11)

3.2 柔顺复杂装备精密产品多质量特性冲突的灰色关联分析

柔顺复杂装备精密产品往往本身具备多个质量特性功能。在早期设计阶段,各质量特性在功能实现方面往往存在相互冲突、矛盾现象,一个质量特性的提升可能导致另一个质量特性下降。因此,在早期设计阶段考虑多质量特性之间的权衡是多质量特性稳健优化设计方案评价的难点问题。接近度灰色关联分析法是据序列曲线几何形状的相似程度来判断比较序列与参考序列的关系紧密程度,已在各领域得到广泛应用。因此,本文通过采用接近度灰色关联分析法计算各质量特性值与期望质量特性值之间的关联系数,将多质量特性转化为以关联度的综合质量特性评价指标。据此,进行优势排序分析,选择关联度最大值所对应的设计方案作为最佳稳健设计方案。

根据接近度灰色关联定理,定义稳健优化设计得出的n个多质量特性解集{yi}作为比较序列{yi}={yi(1),yi(2),…,yi(n)},将各n个单质量特性确定性优化解{yj}作为参考序列{yj=yj(1),yj(2),…,yj(n)},其中i=j=1,2,…,n,n为试验设计组合数。接近关联度主要用于测度序列折线在空间中的接近程度,将比较序列{yi}和参考序列{yj}对应的折线记为yi和yj。令

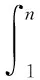
(12)

由比较序列yi和参考序列yj长度相同可得

(13)

根据比较序列{yi}与参考序列{yj}关联度为

(14)

通过接近关联度求出每组非劣解与单质量特性最优解之间的接近关联度,根据关联度值大小选出关联度最大非劣解对应的设计方案作为最终稳健设计方案。

3.3 构造柔顺复杂装备精密产品Gray-PCE稳健优化设计流程

本文基于PCE稳健优化设计模型与接近灰色关联度法相结合来解决不确定性结构参数情形下的柔顺复杂装备精密产品多质量特性波动、冲突的难题,其流程如图4所示,主要分为7个步骤:

步骤1依据柔顺复杂装备精密产品多质量特性工程设计要求及工程实践经验,确定设计变量分布类型及取值范围;

步骤2安排柔顺复杂装备精密产品各设计变量的试验设计组合,据此,根据有限元仿真获得各试验设计组合的多质量特性及最大等效应力响应值;

步骤3依据PCE代理模型的构建思路,构建柔顺复杂装备精密产品多质量特性及最大等效应力的PCE代理模型;

步骤4通过相对误差公式(8)对构建的多质量特性及最大等效应力的PCE代理模型精度进行检验。模型精度检验如果未达到精度要求,则须重新安排试验设计;

步骤5在上述步骤的基础上,采用6σ稳健优化设计建模思路,构建柔顺复杂装备精密产品PCE稳健优化设计模型,并估计多质量特性及最大等效应力模型的均值与方差;

步骤6采用NSGA-Ⅱ算法对柔顺复杂装备精密产品多质量特性PCE稳健优化设计模型进行求解,获取多质量特性非劣解集;

步骤7选择多质量特性非劣解集作为目标矢量序列,各单质量特性最优解作为基准矢量序列,采用接近度灰色关联分析法进行排序,以关联度值最大的多质量特性非劣解所对应的设计方案作为稳健优化设计最佳方案。

图4 柔顺复杂装备精密产品稳健优化设计流程Fig.4 Flowchart of sophisticated equipment products of compliant mechanism robust design optimization

4 案例研究

4.1 柔顺微操作平台多质量特性波动分析

柔顺微操作平台[30]作为典型的柔顺复杂装备精密产品,其三维实体模型如图5所示。该平台主要有两个重要作用,一是通过柔性形变来实现输入微位移的放大;二是通过固有频率实现快速响应。因此,放大倍数和固有频率是本文所需稳健的两个质量特性。柔顺微操作平台依据差动式杠杆放大原理,通过压电陶瓷驱动器对放大机构的微位移产生放大作用来实现其大行程,设计原理如图6所示。根据文献[30]可知,柔顺微操作平台质量特性放大倍数与结构参数间的函数关系表达式:

(15)

式中,t,r分别表示直圆型柔性铰链厚度和半径;L表示杆件Ⅱ的长度;LH表示直角柔性铰链H的长度;yO表示输入位移;yI表示输出位移。

图5 柔顺微操作平台结构示意图Fig.5 Structure of micro-manipulation stage of compliant mechanism

图6 柔顺微操作平台工作原理Fig.6 Working principle of micro-manipulation stage of compliant mechanism

根据柔顺微操作平台在实际复杂工况下,受到环境温度、外界载荷、加工误差、机械振动、材料分布不均匀等外界噪声因子的影响,致使其结构参数呈现不确定性状态,产生多质量特性放大倍数与固有频率波动。同时,柔顺微操作平台操作空间和动态响是相互矛盾和制约的,增加操作空间会提高放大倍数,往往会降低平台的响应速度;反之亦然。为了解决不确定性情形下的放大倍数及固有频率两个质量特性波动及冲突的工程难题,本文采用Grey-PCE多质量特性稳健优化设计新方法来解决这一难题。

4.2 构建柔顺微操作平台随机响应曲面试验设计组合及有限元数值模拟计算

依据柔顺微操作平台多质量特性的工程设计要求与工程实践经验,确定平台结构参数的分布类型与取值范围如表1所示。

表1 不确定性结构参数特性

根据构建PCE代理模型的样本点来源于比其高一阶的正交多项式之根。为了既满足模型预测精度又降低模型复杂度的要求,本文选取PCE代理模型阶次为二阶,可知构建柔顺微操作平台放大倍数、固有频率及最大等效应力PCE代理模型的样本点来源于3阶Hermite正交多项式之根。因此,可获得样本点数量为34的样本空间。然而,这一样本空间的样本量远多于PCE模型展开系数项15项。

从降低有限元数值模拟仿真成本与保证模型精度所需样本量角度考虑,选取样本设计空间内PCE代理模型展开系数项两倍的样本点就能满足模型精度要求。因此,本文依据随机响应面法配点安排30个试验设计组合方案,通过有限元数值模拟仿真平台Ansys workbench 12.1模拟计算各试验设计组合的多质量特性放大倍数与固有频率响应值,同时,模拟各试验设计组合的最大等效应力值。可得柔顺微操作平台各试验设计组合响应值如表2所示。

表2 试验设计组合方案

4.3 构建柔顺微操作平台多质量特性PCE稳健优化设计模型

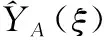
0.000 608ξLξr+0.000 04ξLξt+0.003 45ξLHξr+0.001 34ξLHξt+0.001 22ξrξt

(16)

0.003 69ξLξt-0.092 9ξLHξr-0.006 41ξLHξt-0.014 3ξrξt

(17)

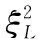
0.040 4ξLξt+0.020 6ξLHξr-0.005 3ξLHξ+0.003 59ξrξt

(18)

根据相对误差式(8)对上述各质量特性与最大等效应力PCE代理模型式(16)、式(17)和式(18)进行模型精度检验。通过20组测试样本点对模型进行检验可得各PCE代理模型相对误差如图7所示。由测试样本相对误差结果都在10%以内,据此,可认为柔顺微操作平台各PCE代理模型满足精度要求即本文所构建的PCE代理模型可替代真实理论模型。

图7 PCE代理模型相对误差Fig.7 PCE surrogate model relative error

根据柔顺微操作平台实际工程设计要求,本文以多质量特性放大倍数、固有频率设为目标函数,最大等效应力为约束函数。同时,依据柔顺微操作平台产生的最大等效应力不应超过柔顺微操作平台材料的屈服极限34 MPa作为约束条件。在给定结构参数取值范围及分布类型,构建柔顺微操作平台多质量特性PCE稳健优化设计模型:

(19)

为了验证本文多质量特性PCE稳健优化设计模型的有效性,同时,本文构建确定性优化设计模型:

(20)

4.4 基于灰色关联度的多质量特性稳健优化方案选择

根据上文建立的柔顺微操作平台多质量特性PCE稳健优化设计模型式(19)与传统确定性优化设计模型式(20),本文基于Isight多学科优化平台对两类模型,采用内嵌NSGA-Ⅱ算法进行求解。多质量特性放大倍数与固有频率稳健迭代寻优过程如图8和图9所示。

图8 放大倍数稳健迭代寻优过程Fig.8 Robust iterative optimization process of the amplification

图9 固有频率稳健迭代寻优过程Fig.9 Robust iterative optimization process of the natural frequency

由于在实际工程中柔顺微操作平台稳健优化求解出的多质量特性解集难于权衡决策,设计方案选择过程往往可能产生多质量特性相互冲突、矛盾的现象,导致难以获得柔顺微操作平台多质量特性综合性能最佳的稳健设计方案。因此,本文采用接近度灰色关联分析法进行分析。首先,分别以放大倍数和固有频率为目标响应求解出无质量特性冲突情形下的各单目标响应稳健优化解集。据此,获取无质量特性冲突情形下的各单目标响应的稳健最优解分别为：放大倍数f1=6.988 5,固有频率f2=95.718 1。

然后,以无质量特性冲突情形下的各单目标响应的稳健最优解作为基准矢量序列,将多质量特性冲突情形下的目标响应解集作为目标矢量序列,根据接近度灰色关联分析法计算目标矢量序列与基准矢量序列之间的关联度。并以灰色关联度最大的目标矢量序列作为稳健最优解即多质量特性解集与各单质量特性最优解集的接近程度,据此,灰色关联度最大对应设计方案即为多质量特性冲突下的稳健最佳设计方案。根据接近度灰色关联分析法计算可得柔顺微操作平台放大倍数与固有频率多质量特性灰色关联度分析结果如表3所示。

4.5 多质量特性稳健优化结果对比分析

根据上述接近度灰色关联分析结果,选择关联度最大的多质量特性稳健最佳解分别为：放大倍数f1=6.845 1,固有频率f2=94.436 9所对应的稳健优化设计方案如表4所示。

表3 多质量特性灰色关联度分析

表4 Grey-PCE稳健优化设计方法结果

从设计方案角度分析表4可知,基于Grey-PCE多质量特性稳健优化设计所获得的各结构参数的稳健性质量水平都达到了6σ水平以上,其对应各结构参数可靠度都近似达到了100%;相比确定性优化设计所得到的结果如表5所示,各结构参数的稳健性质量水平均未达到2σ水平,相应的可靠度都处于70%～90%,难于满足国防、医疗等高尖端领域高可靠性、高稳健性的严苛设计要求。

表5 传统确定性优化设计结果

从多质量特性两类方法均值优化效果角度分析,采用本文提出方法所得到的柔顺微操作平台放大倍数为6.845 1倍,相比确定性优化设计方法所得到的6.967 7倍,两类方法所得到的放大倍数在均值方面相差不大。然而,确定性优化设计方法所得到的放大倍数稳健性质量水平为1.9σ。相比本文方法稳健优化得到的稳健性水平8σ,远远低于Grey-PCE多质量特性稳健优化设计方法所得结果的稳健性;同时,确定性优化设计方法所得到的柔顺微操作平台固有频率为94.234 7 Hz,而本文方法所得固有频率为94.436 9 Hz,在均值方面两者也相差不大。但通过本文方法所得到的固有频率稳健性质量水平为8σ,也远远大于确定性优化结果的3σ水平。且柔顺微操作平台多质量特性Grey-PCE稳健优化设计后的值得到了最大等效应力减小,降低了平台发生失效的概率。从表4和表5最大等效应力稳健性质量水平对比也可体现出。综上分析表明,提高柔顺微操作平台多质量特性稳健可靠性水平,不仅均值要达到多质量特性的目标期望,而且还要降低多质量特性波动。

从多质量特性放大倍数和固有频率的标准差角度分析,基于本文提出的Grey-PCE多质量特性稳健优化设计方法所得到的各质量特性标准差相比确定性优化设计所得到各质量特性标准差要小很多。本文方法所得放大倍数和固有频率标准差分别为0.017,0.126;而相应的确定性优化设计方法所得到的放大倍数和固有频率标准差分别为0.181,1.34。两类方法优化结果对比如图10和图11所示。从图10、图11对比分析可知Grey-PCE多质量特性稳健优化设计方法所得到的各质量特性概率密度曲线更为“瘦小”,说明其标准差值越小,其性能波动就越小,符合高尖端领域严苛的工程设计要求。

图10 柔顺微操作平台放大倍数概率分布对比Fig.10 Comparison of amplification probability distribution of micro-manipulation stage

图11 柔顺微操作平台固有频率概率分布对比Fig.11 Comparison of natural frequency probability distribution of micro-manipulation stage

根据表4和表5综合分析,表明在早期设计阶段,考虑设计参数不确定性及多质量特性相互冲突、矛盾对柔顺微操作平台性能的影响,是实现其在复杂工况下稳健运行前提和基础。由两类方法优化结果对比分析可知,本文所提出的Grey-PCE多质量特性稳健优化设计模型,在设计阶段考虑各结构参数的不确定性分布类型基础上并增加了多质量特性冲突的设计方案权衡分析,相比传统确定性优化设计方案更稳健。

5 结 论

不确定性结构参数情形下的柔顺复杂装备精密产品多质量特性冲突与波动是复杂装备领域的热点与难点问题。为了确保在早期设计阶段,柔顺复杂装备精密产品设计质量的提升,本文针对结构参数不确定性情形下的柔顺复杂装备精密产品多质量特性波动、多质量特性相互冲突工程难题,提出了Grey-PCE多质量特性稳健优化设计新方法。该方法通过柔顺复杂装备精密产品PCE稳健优化设计模型获得多质量特性稳健优化解集;结合接近度灰色关联分析法对稳健优化解集进行接近度灰色关联度分析,根据关联度最大值评价,决策选出最佳稳健优化设计方案。该方法不仅提高了柔顺复杂装备精密产品多质量特性冲突难题,还增强了多质量特性对外界的抗干扰性。为解决了不确定性结构参数情形下柔顺复杂装备精密产品多质量特性冲突及波动难题提供了一种参考依据。

[1] LI Y P, LIU S F, XU L, et al. Decision target adjustment quality function deployment network with an uncertain multi-level programming model for a complex product[J]. Journal of Grey System, 2015, 27(3):132-150.

[2] 李亚平,刘思峰,方志耕, 等. 多质量特性产品参数设计灰靶模型[J]. 中国机械工程, 2016, 27(8): 1078-1083.

LI Y P,LIU S F, FANG Z G, et al. Grey target model for parameter design of multi quality characteristic products[J]. China Mechanical Engineering, 2016, 27(8): 1078-1083.

[3] 孙光永,李光耀,闫晓磊,等.多目标稳健优化设计方法在车身设计制造中的应用研究[J].固体力学学报,2011,32(2):186-196.

SUN G Y, LI G Y, YAN X L, et al. Application research of multi-objective robust optimization for design and manufacture in vehicle body[J].Acta Mechanica Solida Sinica,2011,32(2):186-196.

[4] 谢展, 于德介, 李蓉, 等. 汽车发动机悬置系统的多目标稳健优化设计[J]. 汽车工程, 2013, 35(10): 893-897.

XIE Z, YU D J, LI R， et al. Multi-objective robust optimization design of vehicle engine mount systems[J]. Automotive Engineering, 2013, 35(10): 893-897.

[5] CHEN D, FANG Z G, LIU X Q. Research on multiple-objective weighted grey target reliability optimization model of complex product[J]. Journal of Grey System, 2015, 27(3):11-22.

[6] LI H, GU J, WANG M, et al. Multi-objective optimization of coronary stent using Kriging surrogate model[J]. Biomedical Engineering Online, 2016, 15(2):148.

[7] FANG J, GAO Y, SUN G, et al. Multi objective robust design optimization of fatigue life for a truck cab[J]. Reliability Engineering & System Safety, 2015, 135(135): 1-8.

[8] LI F, SUN G, HUANG X, et al. Multiobjective robust optimization for crashworthiness design of foam filled thin-walled structures with random and interval uncertainties[J]. Engine-ering Structures, 2015, 88(1): 111-124.

[9] AKHTAR T, SHOEMAKER C A. Multi-objective optimization of computationally expensive multi-modal functions with RBF surrogates and multi-rule selection[J]. Journal of Global Optimization, 2016, 64(1): 1-16.

[10] MACKMAN T J, ALLEN C B, GHOREYSHI M, et al. Compa-rison of adaptive sampling methods for generation of surrogate aerodynamic models[J]. AIAA Journal, 2014, 51(4): 797-808.

[11] ALIBRANDI U, ALANI A M, RICCIARDI G. A new sampling strategy for SVM-based response surface for structural reliability analysis[J]. Probabilistic Engineering Mechanics, 2015, 41:1-12.

[12] GASPAR B, TEIXEIRA A P, SOARES C G. Assessment of the efficiency of Kriging surrogate models for structural reliability analysis[J].Probabilistic Engineering Mechanics,2014,37(4):24-34.

[13] KERSAUDY P, SUDRET B, VARSIER N, et al. A new surrogate modeling technique combining Kriging and polynomial chaos expansions-application to uncertainty analysis in computational dosimetry[J]. Journal of Computational Physics, 2015, 286:103-117.

[14] FORRESTER D I A J, SOBESTER D A, KEANE A J. Engineering design via surrogate modelling: a practical guide[M]. London: Antony Rowe, 2008.

[15] FORRESTER A I J, KEANE A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45(1/3): 50-79.

[16] WORTMAN T, COSTA A, NANNICINI G, et al. Advantages of surrogate models for architectural design optimization[J]. Ai Edam Artificial Intelligence for Engineering Design Analysis & Manufacturing, 2015, 29(4): 471-481.

[17] LI X, QIU H, CHEN Z, et al. A local Kriging approximation method using MPP for reliability-based design optimization[J]. Computers & Structures, 2016, 162(C): 102-115.

[18] 欧阳林寒. 模型不确定下的稳健参数设计研究[D]. 南京: 南京理工大学, 2016.

OUYANG L H. Robust parameter design with model uncertainty[D].Nanjing:Nanjing University of Science and Technology, 2016.

[19] 韦东来. 汽车覆盖件成形工艺的稳健优化与容差分析[D]. 上海: 上海交通大学, 2009.

WEI D L. Robust optimization and tolerance analysis of autobody panel stamping[D]. Shanghai: Shanghai Jiaotong University, 2009.

[20] HOWELL L L. Compliant mechanisms[M]. New York: Wiley, 2001.

[21] 万良琪. 考虑设计参数不确定性的6σ稳健优化设计方法及工程应用[D]. 赣州: 江西理工大学, 2016.

WAN L Q. The optimization and engineering application of 6σ robust based on uncertain design parameter[D]. Ganzhou: Jiangxi University of Science and Technology, 2016.

[22] SARMA P, XIE J. Efficient and robust uncertainty quantification in reservoir simulation with polynomial chaos expansions and non-intrusive spectral projection[C]∥Proc.of the SPE Reservoir Simulation Symposium, 2011.

[23] CHEN Y, JAKEMAN J, GITTELSON C, et al. Local polynomial chaos expansion for linear differential equations with high dimensional random inputs[J]. SIAM Journal on Scientific Computing, 2015, 37(1): 79-102.

[24] FRANCIOSA P, GERBINO S, CEGLAREK D. Fixture capability optimization for early-stage design of assembly system with compliant parts using nested polynomial chaos expansion[J]. Procedia CIRP, 2016, 41: 87-92.

[25] HAMPTON J, DOOSTAN A. Compressive sampling of polynomial chaos expansions: convergence analysis and sampling strategies[J]. Journal of Computational Physics, 2014, 280: 363-386.

[26] STROUD A H. Approximate calculation of multiple integrals[M]. Englewood Cliffs, NJ: Prentice-Hall, 1971.

[27] WEBSTER M D, TATANG M A, MCRAE G J. Application of the probabilistic collocation method for an uncertainty analysis of a simple ocean model[J]. MIT Joint Program on the Science and Policy of Global Change, 1996, 4: 1-21.

[28] ACHARJEE S, ZABARAS N. Uncertainty propagation in finite deformations-a spectral stochastic Lagrangian approach[J]. Computer Methods in Applied Mechanics & Engineering, 2006, 195(19/22):2289-2312.

[29] XIONG F, XUE B, YAN Z, et al. Polynomial chaos expansion based robust design optimization[J]. International Conference on Quality, Reliability, Risk, Maintenance, & Safety Engineering, 2011, 412(8): 868-873.

[30] SINGH T, SINGLA P, KONDA U. Polynomial chaos based design of robust input shapers[J]. Journal of Dynamic Systems Measurement & Control, 2010, 132(5): 626-634.

[31] 徐贵阳. 基于响应面法的微操作平台设计与性能综合[D]. 赣州: 江西理工大学, 2015.

XU G Y. Design and performance synthesis of micro-manipulation stage based on response surface method[D]. Ganzhou: Jiangxi University of Science and Technology, 2015.