基于理想弹道鲁棒容积卡尔曼滤波视线角估计

刘振亚, 高 敏, 程 呈

(陆军工程大学导弹工程系, 河北 石家庄 050003)

0 引 言

全捷联导引头相比于传统平台式导引头具有体积小、质量轻、可靠性高[1]等特点,满足精确打击武器低成本、小型化的要求,被广泛应用于现代化局部战争中。由于全捷联导引头将探测器与弹体固连,弹目视线角与弹体姿态角相互耦合,导致探测器不能直接输出制导控制系统所需的弹目视线角以及弹目视线角速率。通过建立坐标系转换关系,可将探测器测量得到的体视线角解耦得到弹目视线角以及弹体姿态角,将惯性测量组件测量得到的弹体姿态角代入解耦方程中,即可得到弹目视线角。而导引头探测元件受环境扰动影响大,导致测量得到的体视线角很可能偏离真实值。同时,惯性测量组件测量得到的弹体姿态角也具有一定的噪声,使得直接解耦得到的弹目视线角误差较大。

目前,国内外学者对于全捷联弹目视线角信息估计问题已经研究的比较深入,针对系统具有非线性的特点,主要利用非线性卡尔曼滤波对弹目视线角进行估计。文献[2]针对非线性目标运动模型,利用扩展卡尔曼滤波的方法对目标运动信息进行了估计;文献[3]针对滤波器初始值不准确以及异常值的存在,提出了一种鲁棒参数化范围容积卡尔曼滤波(cubature Kalman filter,CKF)的纯方位跟踪方法;文献[4]通过对扩展卡尔曼滤波、无迹卡尔曼滤波、中心差分卡尔曼滤波以及粒子滤波在目标跟踪问题中的性能进行了分析,从而为在实际应用中如何选择非线性滤波器提供了理论依据。文献[5]分别利用微分网络以及卡尔曼滤波对弹目视线角进行仿真,表明卡尔曼滤波具有更小的延迟与噪声水平;文献[6]为分析全捷联图像导引头视线角速率精度影响因素,提出了视线角速率解耦算法,并根据误差理论详细分析了各误差源的误差灵敏度;文献[7]以捷联红外导引头的工程应用为研究背景,针对刻度尺误差带来的隔离度问题,提出一种基于多模型的隔离度在线补偿方法。

在工程应用中,所建立系统与实际模型存在误差,且噪声的统计特性未知,造成估计结果误差较大甚至发散。针对上述问题,许多学者对卡尔曼滤波器进行了改进。文献[8]针对离散线性系统状态方程以及量测方程具有不确定性问题,将估计误差协方差有界作为条件,得到协方差最小时的增益矩阵;文献[9]针对将模型最大不确定度作为条件滤波结果保守程度大的问题,利用帕累托效率权衡滤波器的滤波性能以及鲁棒性能;文献[10]针对具有模型不确定性的非线性系统,将非线性系统线性化,得到鲁棒扩展卡尔曼滤波算法。文献[11]针对具有多传感器的模型不确定系统,将噪声与参数不确定性统一转化为噪声不确定性,利用极大极小鲁棒估值原理,提出一种鲁棒协方差交叉融合稳态卡尔曼滤波器,文献[12]通过对卡尔曼滤波器的实时性能评价,提出了一种基于非线性映射的自适应调节权值混合Kalman/H∞滤波器;文献[13]为减小测量异常误差对非线性目标跟踪系统的影响,提出了一种基于广义M估计的鲁棒容积卡尔曼滤波(robust cubature Kalman filter,RCKF)算法。

上述弹目视线角估计方法都需要惯性元件对弹体运动参数进行测量,但目前的测量元件成本高,抗高过载能力低,精度受环境影响较大,因此其在低成本全捷联制导弹药中的应用难度极大。本文针对全捷联制导弹药飞行弹道基本固定的特点,将理想弹道参数视为带不确定性的模型参数,提出了一种基于理想弹道的鲁棒容积卡尔曼滤波(ideal trajectory robust cubature Kalman filter,ITRCKF)的弹目视线角估计算法。

1 坐标系定义及转换

(1) 如图1(a)所示,O-xgygzg为基准坐标系,坐标系原点O为弹体质心位置,Oxg轴沿水平线指向射击方向,Oyg轴铅直向上,Ozg根据右手法则垂直于Oxgyg平面指向右方。

(3) 如图1(a)所示,O-xqyqzq为视线坐标系,坐标原点O为弹体质心位置,Oxq轴与弹目连线重合并指向目标,Ozq轴在基准系Oxgzg平面内且与Oxq轴垂直,Oyq轴按照右手法则与Oxqzq平面垂直向上。Oxq轴与水平面夹角为弹目视线倾角qγ,其水平面投影与基准坐标系Oxg轴夹角为弹目视线偏角qλ。

(5) 如图1(b)所示,O-xlylzl为体视线(body line-of-sight,BLOS)坐标系,坐标原点O为弹体质心位置,Oxl轴与弹目视线重合指向目标,Ozl轴在弹体坐标系Oxbzb平面内且与Oxl轴垂直,Oyl根据右手法则与Oxlzl平面垂直向上。Oxl轴与弹体坐标系Oxbzb平面夹角为体视线倾角qα,其在Oxbzb平面的投影与弹体坐标系Oxb轴的夹角为体视线偏角qβ。

图1 坐标系定义Fig.1 Definition of coordinate

坐标系之间的关系可由各坐标系之间的夹角确定,利用坐标系连续旋转的方法即可得到各坐标系之间的转换关系以及转换矩阵。图2为上述5种坐标系之间的转换关系,其中L(·)为各坐标系之间的转换矩阵。

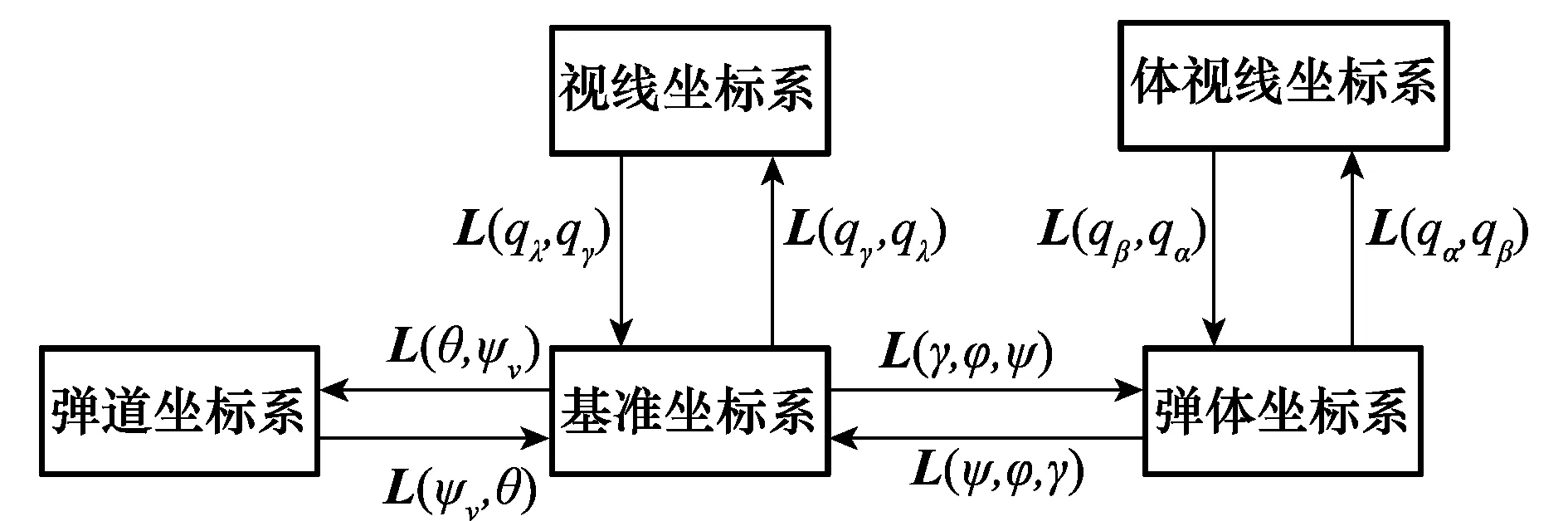
图2 坐标系转换关系Fig.2 Relationships of coordinate systems

2 滤波模型建立

2.1 弹目相对运动模型

设弹目相对运动矢量r,弹体速度矢量vm,目标运动矢量为vt,其变化规律可表示为

(1)

根据制导弹药目标为固定点可得:vt=0;将弹体速度矢量vm投影到视线坐标系Oxq、Oyq与Ozq三轴,根据弹目相对运动角速度与线速度的关系,可得弹目相对运动速度表达式为

(2)

式中,vx、vy与vz为弹体速度在视线坐标系下的投影。

已知弹体速度在弹道坐标系下的坐标为(v,0,0),为求得弹体速度矢量在视线坐标系下的投影,根据图2中坐标系间的转换关系,可得到基准系下弹体以及目标的速度矢量在视线坐标系下坐标:

(3)

将坐标系转换矩阵代到式(3)中,结合式(2),最终可得到弹目相对运动速度的表达式为

(4)

2.2 滤波器观测模型

(5)

最终化简得到滤波器观测模型为

(6)

式中,Rij为基准坐标系至弹体坐标系转换矩阵中的元素；v1和v2为导引头量测噪声。因此,滤波模型由状态方程(4)和量测模型(6)组成,其中状态变量为弹目相对运动信息,量测值为探测器测量得到的体视线角。

3 鲁棒容积卡尔曼滤波

3.1 非线性系统线性化

建立具有不确定参数的离散非线性系统:

(7)

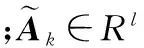
(8)

利用泰勒公式将非线性系统状态方程以及量测方程在滤波器状态估计点处展开,得到的线性系统:

(9)

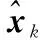
3.2 非线性不确定参数线性化

由式(9)可以看出,利用泰勒公式展开级数的一阶项系数为关于不确定参数的非线性函数。现将状态方程一阶项不确定系数表示为

(10)

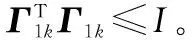
将该系数利用泰勒公式展开可得

(11)

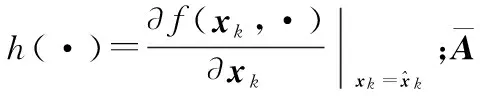
(12)

式(12)右边项中的不确定度完全由非线性系统中参数不确定度ΔAk决定,因此可设定

高中物理实验教学中通过合作式的学习方法帮助学生培养合作思维能力.在一个物理实验过程中往往有许多实验步骤需要几人合作完成，通过合作式的学习方法让学生体会到合作的重要性，在今后的学习和工作过程中能够明白通过与他人合作解决问题或是实现目标.高中物理教育中物理实验的合作式学习方法能够有效地培养学生的合作思维能力.

(13)

同理,设定量测方程一阶不确定系数为

(14)

根据式(9)～式(14),最终得到带不确定参数线性化系统表达式:

(15)

3.3 误差协方差矩阵

(16)

利用CKF算法[14]可得系统状态的一步预测估计值为

(17)

将状态变量线性化表达式(9)以及CKF得到一步预测状态量式(17)代入一步预测误差表达式,可得

(18)

根据状态预测误差协方差定义,可得一步预测误差协方差表达式为

Pk+1|k=(F1k+M1kΓ1kN1k)Pk|k(F1k+M1kΓ1kN1k)T+Q

(19)

系统观测估计值为

(20)

将系统观测值代入至输出预测误差表达式(16)中,可得

(21)

输出预测误差协方差为

Py,k+1=

(F2k+M2kΓ2kN2k)Pk+1|k(F2k+M2kΓ2kN2k)T+R

(22)

设定状态变量量测更新表达式为

(23)

易得状态误差协方差表达式

(24)

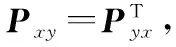
(25)

(26)

3.4 RCKF的设计

引理1[15]存在具有合适维度的矩阵A,B,C和D,并且满足CCT≤I。若任意给定一个实正定矩阵以及一个正常数κ,并且满足κI-DUDT>0;那么有式(27)成立

(A+BCD)U(A+BCD)T≤

A(U-1-κ-1DTD)-1AT+κBBT

(27)

根据引理1对式(19)及式(22)进行变换,得到带不确定参数的一步预测误差协方差以及输出预测误差协方差的上界Σk+1|k和Σy,k+1，其表达式为

(28)

(29)

当一步预测协方差满足Pk+1|k≤Σk+1|k,则状态误差协方差满足Pk+1≤Σk+1[16]。因此,只需选择合适的增益矩阵将误差协方差矩阵上界的迹最小化,即将式中的P用Σ代替,就可得到参数不确定系统状态估计的误差协方差最小上界。

(30)

(31)

根据式(30)与式(31),利用球面径向准则计算容积点Xi与Yi,最终可得

(32)

(33)

(34)

将上述协方差矩阵上界代入第3.3节的结论中,可以得到RCKF算法:

(1) RCKF初始化

(35)

(2) 计算容积点

(36)

(37)

式中,n表示状态变量的个数;[1]i表示一个全对阵点集。例如,当n=2时,全对阵点集可表示为

(3) 容积点传播

Xi,k+1/k=f(Xi,k/k,uk)

(38)

(4) 状态预测以及误差协方差

(39)

计算容积点

(40)

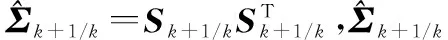
(5) 容积点传播

Yi,k+1/k=g(Xi,k+1/k,uk)

(41)

(6) 量测值估计、量测协方差以及状态量测交叉协方差

(42)

(7) 滤波更新方程

(43)

3.5 不确定性参数κ的选择

引理1中用含不确定性参数γ的协方差矩阵表示系统含参数不确定性的状态误差协方差矩阵的上界。因此,选择合适的不确定参数对于滤波性能的好坏以及滤波稳定性能有着至关重要的作用。

在RCKF算法中,式(30)与式(31)限制了κ的下限,κ必须大于矩阵N-1Σ(NT)-1的最大特征值,一般矩阵N取单位阵,即:

κ>max(eig(Σ))

(44)

(1) 当κ≫max(eig(Σ))时,满足算法中的条件。但这时(Σ-1-κ-1NTN)-1近似不变,而κMMT趋于无限大,这时系统误差协方差矩阵对于系统的不确定性没有了限制,该算法失效。

(2) 当κ=max(eig(Σ))+δ时,其中δ为任意小量,这时max((eig(Σ-1-κ-1NTN)-1))远大于max((eigΣ-1)),随着迭代步骤的增加,误差协方差矩阵趋于发散,并且发散速率随着δ值的减小逐渐加快。

(3) 当系统中n个状态变量的协方差矩阵之间数量级相差较大,而κ需要满足条件κ>max(eig(Σ)),由不等式(28)可知,较大的κ为数量级较小的状态变量协方差定义了较大的上界,从而使算法对于协方差数量级较小的状态变量估计值具有较大的保守性,导致在滤波结果中,某些元素的精度比其他元素要高。

4 基于理想弹道参数的弹目视线角估计算法

针对制导弹药弹体运动弹道基本固定的特点,可将理想弹道的弹体运动参数作为带有不确定性的实际飞行运动参数,利用RCKF算法对弹目视线角进行估计,可将导引头内的惯性测量组件减少或去掉,进一步降低了全捷联制导弹药的成本,提高其可靠性能。

4.1 实际运动参数误差分析

由式(13)可知,非线性滤波系统式(4)和式(6)不确定度仅与系统中参数不确定度有关。因此,当实际弹体运动参数与理想弹道参数误差越小,滤波系统不确定度对于滤波结果的影响越小。现以初始射角为85°对某型迫击炮弹进行1 000次蒙特卡罗模拟打靶实验,分析实际弹道参数相对于理想弹道参数误差的大小。需要注意的是,由于仅对弹目视线角进行估计,因此可将弹目相对距离作为系统参数。

通过对实验结果的拟合,得到除滚转角外的弹体运动参数服从以理想弹体运动参数为均值的正态分布,其标准差变化曲线如图3所示。

图3 弹体运动参数误差标准差曲线Fig.3 Variance of projectile motion parameter error

4.2 基于理想弹道参数的滤波器设计

根据式(4)及式(6),可分别得到非线性系统系统状态方程以及量测方程对于状态变量的雅克比矩阵

(45)

式中,f1和f2分别表示为系统状态方程中关于弹目视线角的方程;g1和g2分别表示系统量测方程中的两个方程。

可将矩阵U和V看作线性化系统系数,可得状态方程与量测方程线性化系数对于系统不确定参数(即弹体运动参数)的雅克比矩阵

(46)

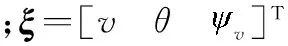
根据式(12),可得滤波系统不确定度

(47)

式中,M1Γ1N1为状态方程不确定度;M2Γ2N2为量测方程不确定度;Δξ和Δη为实际弹道参数与理想弹道参数之间的偏差值。在设计滤波器时,Δξ和Δη取利用蒙特卡罗仿真的方法计算每条实际弹道与理想弹道在对应时刻误差的标准差,作为系统不确定度的上界。

根据所建立的滤波器模型,最终得到基于理想弹道参数的弹目视线角滤波估计算法。为区分滚转角,将不确定参数设定为κ,其算法过程如图4所示。

图4 弹目视线角估计算法流程图Fig.4 Estimation algorithm flow of LOS angle

5 实验验证

5.1 数字仿真实验

为验证弹目视线角估计精度以及算法的性能,首先构建图5所示的仿真验证模型。其中,弹体六自由度运动模型根据某型迫击炮弹体气动参数以及实际打靶测得的射击环境构建;弹目相对运动模型以及导引头模型分别由系统状态方程(4)与量测方程(6)建立;目标模型设定为目标点位置(1 000,0,0),滤波估计模型由RCKF算法构建,其初始值为导引头开始工作时刻的理想弹道弹目视线角。在满足不等式(44)的条件下,设定鲁棒滤波器中不确定参数为

κ=100max(eig(Σ))

(48)

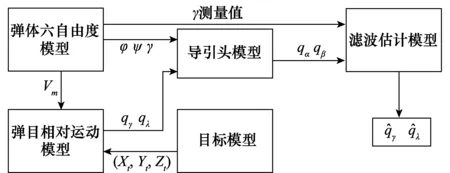
图5 仿真实验模型示意图Fig.5 Simulation model sketch

弹道参数不确定性主要由弹体质量、转动惯量、气动参数、发射角偏差、初始速度偏差以及风速风向扰动因素造成。由于弹体质量、转动惯量以及气动参数不确定范围较小,因此在本次实验中忽略这三种扰动因素,分别设定小扰动条件与大扰动条件如表1所示。

表1 实验条件

其中Δv表示初始速度偏差,Δangle表示射角偏差,ΔAwind表示风向扰动偏差,Δwind表示风速系数(即风速扰动=发射环境测量得到的风速×风速系数)。将某型迫弹作为实验对象,其在弹道末段的速度约为200 m/s,而激光导引头的探测距离约为2 km,因此设定滤波器工作时间为10 s,设定初始射角为85°,分别在上述小扰动以及大扰动条件下进行数字仿真实验。

5.2 实验结果分析

实验结果如图6、图7及表2所示,仅利用理想弹道参数与CKF对弹目视线角进行滤波估计的实验结果,将理想弹道参数作为滤波器系数对弹目视线角进行估计的结果误差并没有很大,主要是由于制导弹药弹道基本固定,并且参数不确定性较小,在弹道末端,无论系统参数是否确定,其弹目视线倾角基本保持在接近于-90°的范围内并最终迅速趋于0°。因此随着时间变化其误差逐渐趋于零;而弹目视线偏角在弹道末端随着弹目相对距离的减小,其值逐渐增大并逐渐趋于落点与目标点的夹角,因此随着弹目相对距离的接近,理想弹道偏角与实际弹道偏角的误差越来越大。

当弹体受到小扰动的实验结果如图6所示,对比其中仅依靠CKF的弹目视线偏角估计值曲线与ITRCKF弹目视线估计值曲线,可以看到:ITRCKF对于弹目视线倾角估计效果相对于CKF并不是很明显,其主要原因是在小扰动条件下弹目视线倾角在弹道末端的变化范围小,不确定性对其影响较小;而ITRCKF对于弹目视线偏角估计值有着较好的抗系统不确定性,由表2中结果可知,ITRCKF滤波估计最大误差值较CKF下降了85.57%,误差均方根下降了81.93%。

图6 小扰动条件实验结果Fig.6 Experiment result in small disturbance

图7 大扰动实验结果Fig.7 Experiment result in large disturbance

条件CKF最大误差/(°)RCKF最大误差/(°)CKF误差均方根/(°)RCKF误差均方根/(°)小扰动qγ0.260.230.180.17大扰动qγ3.782.582.331.25小扰动qλ2.910.421.660.30大扰动qλ2.342.961.422.67

对比在大扰动条件下ITRCKF对于弹目视线倾角的估计结果,可以看到在大扰动的条件下ITRCKF具有更好的滤波结果,其平均误差较CKF下降了31.64%,误差均方根下降了46.39%;而对于视线偏角的估计效果并不明显,主要是由于为保证视线倾角估计精度,滤波系统取较大的κ值,使视线偏角估计具有较大的保守性,其滤波结果没有CKF效果好。

综上所述,ITRCKF在对于弹目视线角估计时,对于受扰动影响较大的角度有着明显的鲁棒性能,同时也为另一角度带来了保守性;但相对于CKF滤波结果,其保守性对于滤波精度影响较小。因此,利用ITRCKF能够得到精确的弹目视线角,并且具有较好的鲁棒性能。

6 结 论

本文提出了一种基于理想弹道参数的弹目视线角估计方法,利用理想弹道参数替换惯性元件测量值,减小了导引头体积,降低了导引头成本。针对所建立非线性滤波系统参数具有不确定性,提出了带不确定参数的RCKF方法,将带不确定性系统状态估计问题转化为求解带参数κ的状态变量误差协方差矩阵上界的最小值问题,作为最终得到具有一定精度的弹目视线角,利用数字仿真证明了该算法的稳定性与可行性,并分析了该算法对于弹目视线角抗系统不确定性的有效性与保守性,为低成本全捷联制导弹药制导信息估计提供了理论依据。

[1] JAMES M M. Line of sight rate estimation for guided projectiles with strapdown seekers[J].AIAA Guidance, Navigation and Control Conference, 2015，32(6):2346-2351.

[2] VADDI S S, MENON P K. Target state estimation for integrated guidance-control of missiles[C]∥Proc.of the AIAA Guidance, Navigation and Control Conference and Exhibit, 2007: 1-22.

[3] WU H, CHEN S X, YANG B F, et al. Robust range-parameterized cubature Kalman filter for bearings-only tracking[J]. Journal of Central South University, 2016, 23 (6): 1399-1405.

[4] KATKURI J R, JILKOV V P, Li X R. A comparative study of nonlinear filters for target tracking in mixed coordinates[C]∥Proc of the 42nd South Eastern Symposium on System Theory, 2010: 202-207.

[5] 王伟, 林德福, 徐萍. 捷联导引头弹目视线角速率估计[J]. 红外与激光工程, 2015, 44 (10): 3066-3069.

WANG W,LIN D F,XU P.Strap-down seeker LOS angular rate estimation[J].Infrared and Laser Engineering,2015,44(10):3066-3069.

[6] 孙婷婷, 储海荣, 郭立红, 等. 全捷联图像导引头视线角速率精度分析[J]. 仪器与仪表学报, 2015, 36(7): 1479-1487.

SUN T T, CHU H R, GUO L H, et al. Line-of-sight angular rate accuracy analysis of strapdown imaging seeker[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 1479-1487.

[7] 宗睿,林德福,王伟,等.基于多模型的捷联红外导引头隔离度在线补偿方法[J].系统工程与电子技术,2017,39(3):147-155.

ZONG R, LIN D F, WANG W, et al. Multiple model based online compensation for disturbance rejection rate of strapdown infrared seeker[J]. Systems Engineering and Electronics, 2017, 39(1),147-155.

[8] SHADY M K M, SAEID N. Robust finite-horizon Kalman filter for uncertain discrete-time systems with uncertain observations[J]. IEEE Trans.on Automatic Control, 2012, 57 (6):1548-1552.

[9] XU H, MANNOR S. A Kalman filter design based on the performance/robustness tradeoff[J]. IEEE Trans.on Automatic Control, 2009, 54 (5): 1171-1175.

[10] XIONG K, WEI C L, LIU L D. Rubust Kalman filter for discrete-time nonlinear systems with parameter uncertainties[J]. Aerospace Science and Technology, 2012, 18: 15-24.

[11] 王雪梅,刘文强,邓自立.不确定系统鲁棒交叉融合稳态Kalman滤波器[J]. 电子与信息学报, 2015, 37(8): 1900-1905.

WANG X M, LIU W Q, DENG Z L. Robust covariance intersection fusion steady-state Kalman filter for uncertain systems[J]. Journal of Electronics & Information Technology,2015,37(8): 1900-1905.

[12] 张勇刚, 黄玉龙, 李宁, 等. 基于非线性映射的自适应混合Kalman/H∞滤波器[J]. 系统工程与电子技术, 2013, 35(9): 1948-1953.

ZHANG Y G, HUANG Y L, LI N, et al. Adaptive hybrid Kalman/H∞ filter based on nonlinear mapping[J]. Systems Engineering and Electronics, 2013, 35(9): 1948-1953.

[13] 吴昊,陈树新,杨宾峰,等.基于广义M估计的鲁棒容积卡尔曼滤波目标跟踪算法[J]. 物理学报, 2015, 64(21): 1-7.

WU H, CHEN S X, YANG B F, et al. Robust cubature Kalman filter target tracking algorithmbased on genernalized M-estiamtion[J]. Acta Physica Sinica, 2015, 64(21): 1-7.

[14] ICCKARAN A, SIMON H. Cubature Kalman filters[J]. IEEE Trans.on Automatic Control, 2009, 54(6): 1254-1269.

[15] XIE L, SSOH Y C, DE S. Robust Kalman filter for uncertain discrete-time systems[J]. IEEE Trans.on Automatic Control, 1994, 39(6):1310-1314.

[16] THEODOR Y, SHAKED U. Robust discrete-time minmum-variance filtering[J].IEEE Trans.on Signal Process,1996,44(2): 181-189.