飞行器抗饱和鲁棒自适应非线性模型预测控制

王 超, 张胜修, 宋仔标, 杨建业, 吴晓露

(1. 火箭军工程大学士官学院, 山东 青州 262500; 2. 火箭军工程大学自动控制工程系, 陕西 西安 710025)

0 引 言

为了提高生存能力,顺利完成打击任务,在一些特殊飞行段(如发射段、地形跟踪与回避段、末端攻击段)要求巡航飞行器具备在极大的空域进行大机动飞行的能力。如何以先进的控制技术作支撑,设计具有良好控制效果的控制器就显得意义重大。动态逆控制[1]、变结构控制[2]、自适应反步法[3]等目前常见的非线性飞行控制方法,虽鲁棒性较强,但未系统地解决飞行器状态及输入约束问题,容易造成状态及输入超限,影响高机动时的控制性能。基于较准确的辨识模型,自适应非线性模型预测控制(adaptive nonlinear model predictive control,ANMPC)[10-12]可以实现大范围的高精度控制,为解决以上不足提供了一种方法。笔者在文献[13]中设计了带有在线气动参数辨识的自适应非线性预测控制器,实现了气动特性大幅变化条件下飞行器机动飞行时的抗饱和自适应控制。为进一步克服外部扰动的影响并保证估计参数收敛前系统的鲁棒稳定性,算法还必须配合使用鲁棒控制的方法[14-16]。

为此,以一类被控对象的精确参数模型未知且受外界干扰的约束不确定非线性系统为研究对象,研究了一类基于在线参数辨识并带有模糊干扰观测器(fuzzy disturbance observer,FDO)补偿的鲁棒自适应非线性模型预测控制(robust adaptive nonlinear model predictive control,RANMPC)方法(简记为FDO-RANMPC方法)及其在巡航飞行器底层姿态控制系统设计中的应用。

本文首先引入对未知参数向量的限制条件,改进文献[13]中气动特性的辨识方法,以降低参数辨识的保守性;然后以保证系统鲁棒稳定为出发点,将干扰观测器技术、Tube-RMPC控制策略与之前基于动态逆的自适应非线性预测控制相结合,提出了FDO-RANMPC方法;最后用提出的FDO-RANMPC方法设计了巡航飞行器底层的鲁棒自适应抗饱和姿态控制器,并对设计的姿态控制系统进行了仿真验证。

1 具有未知参数限制条件的气动特性参数的在线辨识

1.1 飞行器气动模型

作用在飞行器上的气动力R和气动力力矩M表达式分别为

(1)

(2)

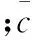
综合考虑模型复杂性与辨识精度,进行折中处理,式(1)和式(2)中的气动系数表达式为

(3)

(4)

式中,δe、δr与δa为飞行器等效控制舵偏角;C*,*为与两个下标有关的气动参数;飞行器飞行中气动特性剧烈变化导致的力和力矩的交叉耦合由方括号内表达式表示。

气动力系数方程表达式(3)及气动力矩系数方程表达式(4)可写成

yF=φTθF+εF

(5)

yM=φTθM+εM

(6)

式中,φ为飞行器状态向量;θF为待估气动力相关参数;θM为待估气动力矩相关参数;εF与εM为相关模型残差;yF为与气动力相关的气动系数;yM为与气动力矩相关的气动系数。

1.2 具有未知参数限制条件的最小二乘气动参数辨识

文献[13]在气动特性的在线辨识中所采用的渐消记忆递推最小二乘(recursive least squares, RLS)参数辨识方法,当初始估计值与实际值相差较大时,就可能造成初始阶段估计误差过大,导致控制效果变差。但实际中根据先验信息或者通过离线辨识的方法往往能提前获知未知参数向量可能接近于某个标定值。故在辨识中可增加对θ*的限制条件,即θ*是n维球体={θ*:║θ*║≤ε}中的一个内点,对一般RLS算法中的性能指标函数进行调整,构造新的性能指标函数:

(7)

式中

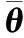
定理1构造最小二乘性能指标函数:

(8)

未知参数向量θ按如下的递推过程得到的RLS估计值使性能指标函数J(θ)最小化。

(1) 参数矩阵更新

i=1→n,T(0)=K(t-1)

(9)

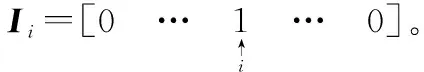
(2) 更新权值矩阵

(10)

(3) 预测误差修正

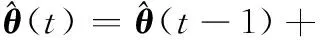
(11)

(12)

证明利用线性代数中矩阵对向量求偏导数的公式,对J(θ)关于θ求导后取值为0,整理得

(13)

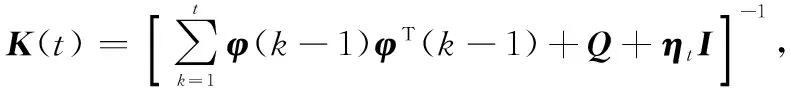
(14)

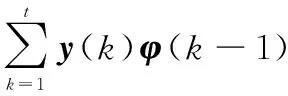
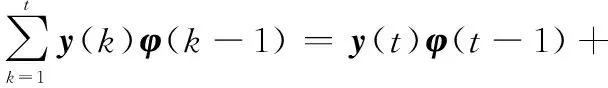
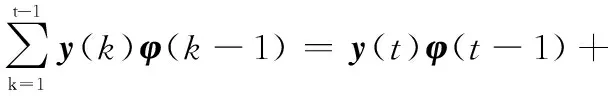
(15)

并将式(15)代入式(13)可得

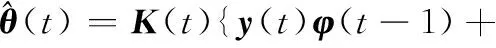
(16)

式(16)整理后即为式(11)。

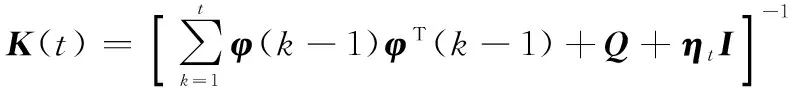
K-1(t)=[K-1(t-1)+φ(t-1)φT(t-1)+(ηt-ηt-1)I]

(17)

用矩阵求逆公式对式(17)两边同时求逆可得

K(t)=[K-1(t-1)+φ(t-1)φT(t-1)+(ηt-ηt-1)I]-1=

[K-1(t-1)+(ηt-ηt-1)I]-1-

[K-1(t-1)+(ηt-ηt-1)I]-1×

[K-1(t-1)+(ηt-ηt-1)I]-1)

(18)

令T(n)=[K-1(t-1)+(ηt-ηt-1)I]-1,式(18)即为式(10)。

再对T(n)使用矩阵求逆引理可得T(n)的递推计算式(9)。

证毕

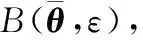
2 基于FDO的鲁棒自适应非线性模型预测控制

考虑到系统中还可能存在诸如未建模动态、外部扰动等非参数不确定性;因而在第1节气动参数在线辨识的基础上,结合ANMPC控制策略,设计飞行器底层姿态系统的控制器并不一定能取得最优的控制效果。因此，还需与鲁棒预测控制方法相结合改善之前间接自适应预测控制的控制效果,保证系统的闭环稳定性。然而当系统所受有界扰动的上界接近鲁棒预测控制容许扰动边界时,鲁棒预测控制的保守性也将随之增大,故本节先设计FDO对包括辨识误差在内的复合干扰有效地逼近,然后将FDO的观测输出应用于RANMPC的设计当中抵消幅值较大的复合干扰,再根据抵消后幅值较小的FDO有界观测误差,设计FDO-RANMPC。

根据飞行器模型[13]的特点,考虑同时含有加性扰动与模型不确定性的约束非线性离散时间系统:

x(k+1)=[f(x(k))+Δf(x(k))]+

[g(x(k))+Δg(x(k))]u(k)+d(k)=

f(x(k))+g(x(k))u+Δ(x(k),u(k))

(19)

式中,x(k)∈Rn为系统状态向量;u(k)∈Rm和y(k)∈Rn分别为系统的输入和输出;函数f(·)与g(·)为基于在线参数估计值的已知光滑非线性函数;Δf(·)和Δg(·)为参数估计误差和非参数不确定性引起的未知光滑函数;d为有界扰动d(k)∈W{d(k)∈Rn|‖d(k)‖∞≤ζ,ζ≥0},ζ表示扰动的上界;Δ(x(k),u(k))为系统不确定和系统所受的外部干扰组成的复合干扰。

系统受如下输入和状态约束条件限制:

M1u(k)≤γ1,k=0,1,…,N-1

(20)

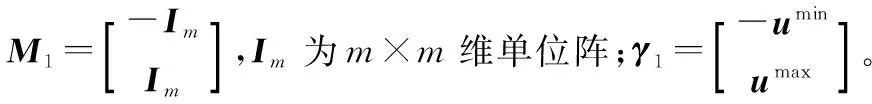
M2x(k)≤γ2,k=0,1,…,N-1

(21)

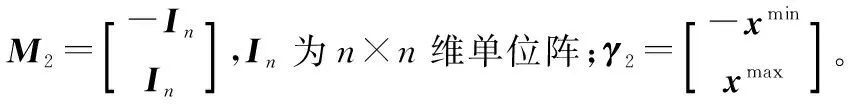
此时先设计基于FDO的自适应非线性预测控制律(FDO-ANMPC),其表达形式为

u(k)=uanmpc(k)+ufdo(k)

(22)

uanmpc(k)=g-1(x(k))(-f(x(k))+v(k))

(23)

(24)

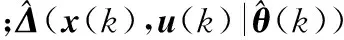
首先给出ufdo的具体形式。在得到ufdo的具体形式后再给出FDO-ANMPC的改进方法,即FDO-RANMPC方法。

(25)

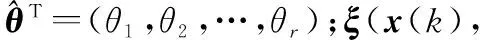
定理2假设系统(19)的控制输入为(22),并且复合误差采用式(26)描述的一阶辅助系统测量:

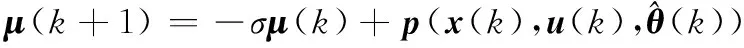
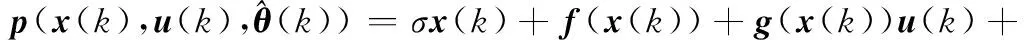
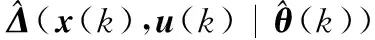
(26)

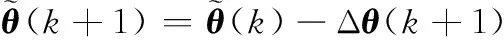
(27)

Δθ(k+1)=-γξ(x(k),u(k))δ(k+1)

(28)

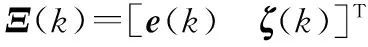
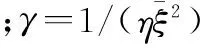
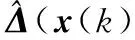
e(k+1)=Ke(k)+c(k)+ε(k)

(29)

可以看出,受干扰观测误差影响,此时FDO-ANMPC优化得到的c(k)并不能保证跟踪误差鲁棒渐近稳定。为克服误差ε对系统的影响,则c(k)需采用鲁棒模型预测控制(robust model predictive control,RMPC)方法设计。由于式(29)为一有界干扰线性系统,故将关于c的约束改写为规范的多面体形式后[13],采用Tube可达集RMPC控制策略[19],可以很容易的给出c(k)的最优鲁棒控制形式。当用其替换式(23)的uanmpc中的c(k)时,FDO-RANMPC控制律可以表示为

u(k)=uranmpc(k)+ufdo(k)

(30)

uranmpc(k)=g-1(x(k))(-f(x(k))+vr(k))

(31)

式中,uranmpc为基于Tube可达集RMPC控制器的优化输出;vr(k)为相应的鲁棒虚拟控制输入;ufdo为FDO的输出。

值得指出的是,从FDO的稳定性证明过程可知,其自身稳定性及增广误差的一致最终有界性与c(k)的具体值无直接关系,因此改进后的控制律并不影响FDO系统的闭环稳定性及增广误差的一致最终有界性。

3 飞行器底层姿态系统FDO-RANMPC控制器设计

在气动参数在线辨识的基础上,结合所提的FDO-RANMPC控制策略,在考虑飞行器状态及控制舵面饱和约束的条件下,设计其底层姿态系统的FDO-RANMPC控制器,为其大机动飞行提供鲁棒、可靠、稳定的飞行保障。

首先基于时标分离思想对飞行器的状态变量进行划分[20-21],如表1所示。

表1 基于时标分离的状态变量

基于本文所研究飞行器的动力学方程

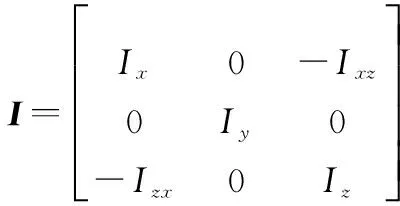
将式(4)变换为

(33)

并将其代入式(32),并根据本文所提FDO-RANMPC控制原理,整理为关于控制量u的仿射非线性形式,可得如式(22)描述的第一层(极快变量层)的控制量:

(34)

(36)

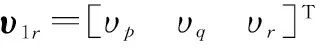
根据飞行器运动状态方程[13]中关于φ的表达式,可得滚转角φ的变化率与旋转角速度间的关系式:

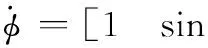
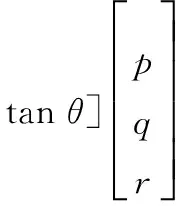
(37)

根据近似关系式:

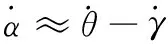
(38)

及航迹倾角定义:

(39)

可得到关系式:

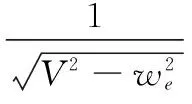
(40)

根据飞行器运动状态方程[13]中关于θ的表达式,可得

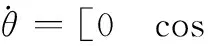
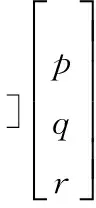
(41)

联合式(38)、式(40)、式(41),可得到攻角α的变化率与旋转角速度间的关系式:

φcosθ+

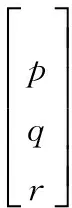
(42)

同样,根据关系式:

v=Vsinβ

(43)

可得侧滑角β的变化率与旋转角速度间的关系式:

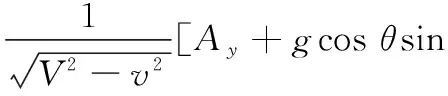
(44)

综合式(37)、式(42)、式(44),根据FDO-RANMPC控制原理可得第二层(快变量层)控制形式:

(45)

f2(x)=

(46)

(47)

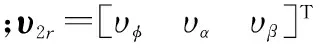
对于第三层(慢变量层),经坐标系相似变换即可得期望快变量信号[20-21]。故跟踪由设计导引律给出的期望速度信号x3d为本层的主要控制目标。

考虑飞行器速度表达式:

(48)

对式(48)两边求导得

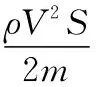
(49)

式中,δT为油门信号;CT为发动机推力指令函数。

将式(49)整理为关于δT的仿射非线性形式,根据FDO-RANMPC可得速度回路控制形式:

(50)

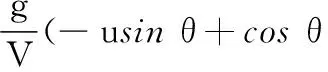
(51)

(52)

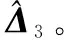
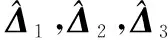
基于FDO-RANMPC的飞行器底层姿态系统控制器结构示意图如图1所示。

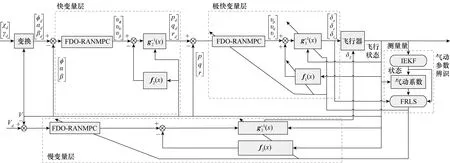
图1 基于FDO-RANMPC的飞行器姿态控制器结构图Fig.1 Structure of the aircraft attitude system Controller based on FDO-RANMPC

4 仿真结果与分析

以巡航飞行器为被控对象,应用上述FDO-RANMPC控制方案,设计飞行姿态控制器,控制效果通过对指令姿态角的跟踪情况进行仿真验证。仿真中模拟飞行器气动参数受到扰动的平均气动模型误差(average aerodynamic modeling errors,AAME)、控制系统设计要求、仿真设置及仿真初始条件均与文献[13]中相同。为模拟外部扰动对FDO-RANMPC飞行控制器的影响,假设快变量层通道受到如下外部有界力矩的干扰(单位:N/m)。

{10sin(2t+0.3) 50[cos(2t)+sin(5t)] 15sin(2t)}

(53)

在Matlab/Simulink环境中,分别对ANMPC(仿真条件1)、RANMPC(仿真条件2)及FDO-RANMPC(仿真条件3)设计的姿态控制器控制效果进行了仿真(预测时域及控制时域长度在3种仿真条件下均取为N=20,即向前预测20步),以对比检验各控制器的控制效果和控制鲁棒性。

仿真结果如图2～图4所示。其中,指令姿态角跟踪效果在3种仿真条件下的对比如图2所示;图3为相应姿态角速律变化情况的仿真对比;图4为相应控制舵面的响应信号。从仿真结果中可以看出:

(1) 控制系统对模型参数不确定性和外部干扰的鲁棒性强。从图2、图3中可以看出,在系统具有复合干扰的情况下,仿真条件1虽然具有气动参数自适应环节,能抵消一部分参数不确定性对系统的影响,但由于缺乏对外部干扰的处理能力,因此气动模型辨识误差和外部干扰的双重作用,明显使系统响应受到影响,无法很好地跟踪参考指令,表现为信号过渡过程时间较长有明显振荡,且含有较大稳态误差。而仿真条件2中加入的鲁棒控制环节能够大幅消减外部干扰等不确定性因素对控制性能的影响,从而提高系统的鲁棒性,使控制性能得到了明显的改善;但由于不带FDO补偿,考虑到辨识误差与外部干扰的幅度仍比较大,鉴于鲁棒控制在处理系统较大不确定性时保守性强的不足,故对指令姿态的跟踪还存在一定的误差。在加入FDO补偿环节后,抵消了幅值较大的不确定性,仿真条件3的系统响应能迅速跟踪上指令姿态信号,仿真条件2中攻角最大5%的的超调量已降低到基本无超调量,加入FDO补偿后的滚动角与侧滑角具有较小的超调量和稳态误差,响应能够稳定,改善了仿真条件2中滚动角与侧滑角存在的幅度维持在0.3o数量级上的振荡现象。

(2) 控制系统具有较好的状态及输入约束处理能力。从图3与图4中可以看出,对于FDO-RANMPC控制器,虽然复合干扰使控制舵面偏转信号出现小幅增加并伴有小幅震荡,但不论指令姿态角发生多大的角度变化,姿态角速率一直处于设计要求的幅值范围内,控制舵面偏转角度也未出现饱和现象,未对飞行器控制造成明显影响。

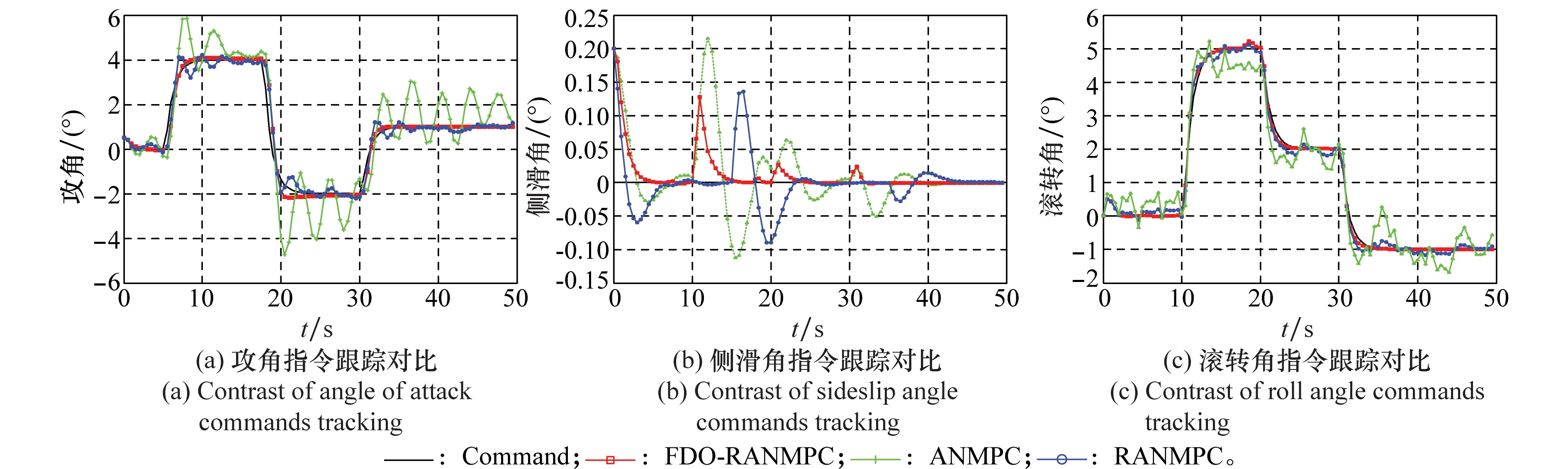
图2 姿态角指令跟踪对比Fig.2 Contrast of angular commands tracking

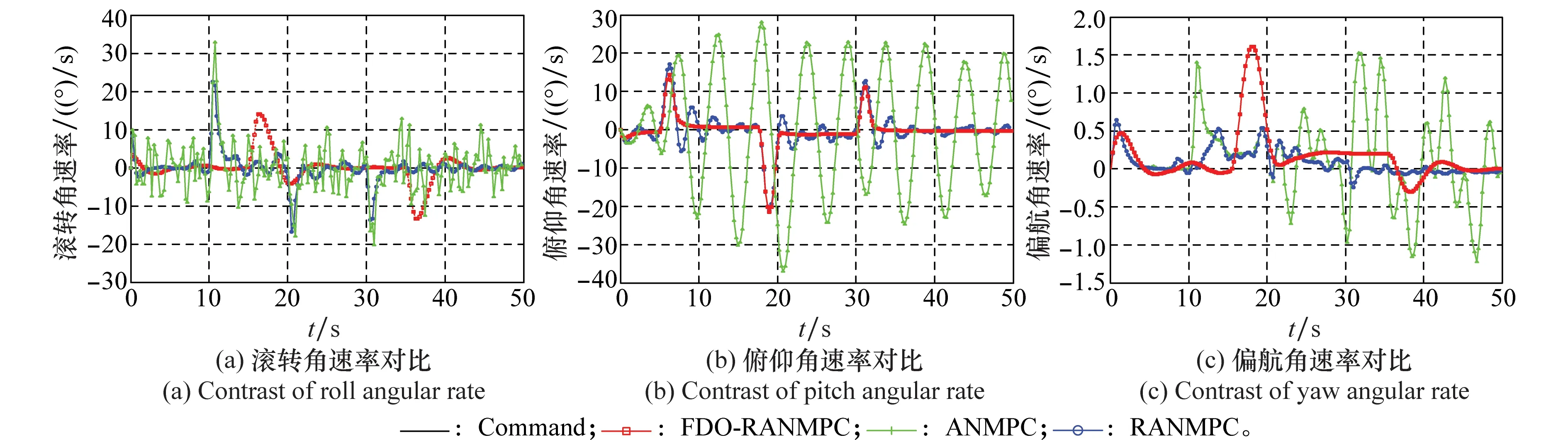
图3 角速率变化情况对比Fig.3 Contrast of body angular rates

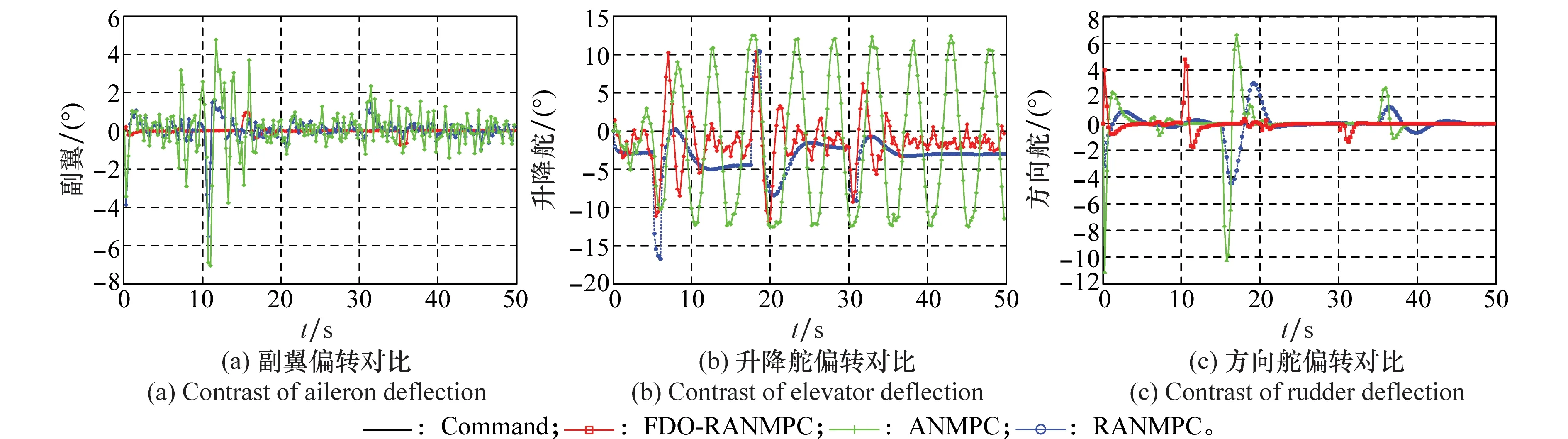
图4 控制舵面偏转对比Fig.4 Contrast of control surface deflection

5 结 论

本文以无人机姿态的控制问题为研究背景,针对一类同时存在模型参数不确定性和较大外部干扰的约束非线性系统,研究基于在线参数辨识并带有模糊干扰观测器补偿的鲁棒自适应非线性预测控制方法,并将该方法成功应用于巡航飞行器含有复合不确定性时的大机动飞行控制中,设计了底层姿态系统FDO-RANMPC控制器。最终基于仿真对比试验对其控制效果进行了验证,从对结果的分析中得出的主要结论有:

(1) 仿真分析表明,RANMPC可以获得比仅含参数自适应环节的ANMPC更好的控制效果;而相比不带FDO的RANMPC,带有FDO补偿机制的FDO-RANMPC利用FDO输出值抵消幅值较大的复合干扰,弥补了RANMPC在处理不确定性时保守性强的不足,最终得到的FDO-RANMPC策略,能在保证系统状态渐进稳定的基础上兼顾对不确定性处理的灵活性。

(2) FDO-RANMPC方法让系统在达到控制目标之余也能够满足所有的约束条件,为具有不确定且受诸多约束条件限制的飞行器高性能飞行控制提供了一种新的卓有成效的技术途径。

[1] LUNGU R, LUNGU M. Adaptive flight control law based on neural networks and dynamic inversion for micro-aerial vehicles[J]. Neurocomputing, 2016, 199(C):40-49.

[2] LU P, KAMPEN E J V, VISSER C D, et al. Aircraft fault-tolerant trajectory control using incremental nonlinear dynamic inversion[J]. Control Engineering Practice, 2016, 57:126-141.

[3] MULLEN J, BAILEY S C C, HOAGG J B. Filtered dynamic inversion for altitude control of fixed-wing unmanned air vehicles[J]. Aerospace Science & Technology, 2016, 54:241-252.

[4] GUO Z, ZHOU J, GUO J. Robust autopilot design for bank-to-turn missiles using adaptive dual-layer sliding mode control[J]. Optik-international Journal for Light and Electron Optics, 2017, 131:383-398.

[5] DEHGHANI M A, MENHAJ M B. Integral sliding mode formation control of fixed-wing unmanned aircraft using seeker as a relative measurement system[J]. Aerospace Science & Technology, 2016, 58:318-327.

[6] AWAD A, WANG H. Roll-pitch-yaw autopilot design for nonlinear time-varying missile using partial state observer based global fast terminal sliding mode control[J]. Chinese Journal of Aeronautics, 2016, 29(5): 1302-1312.

[7] WANG Z, WU Z, DU Y. Robust adaptive backstepping control for reentry reusable launch vehicles[J]. Acta Astronautica, 2016, 126:258-264.

[8] SU Z, WANG H, YAO P, et al. Back-stepping based anti-disturbance flight controller with preview methodology for autonomous aerial refueling[J]. Aerospace Science & Technology, 2016, 61:95-108.

[9] SWARNKAR S, KOTHARI M. A simplified adaptive backstepping control of aircraft lateral/directional dynamics[J]. IFAC Papersonline, 2016, 49(1):579-584.

[10] CHEN P, WANG J. Estimation and adaptive nonlinear model predictive control of selective catalytic reduction systems in automotive applications[J].Journal of Process Control,2016,40:78-92.

[11] WANG P, YANG C H, TIAN X M, et al. Adaptive nonlinear model predictive control using an on-line support vector regression updating strategy[J]. Chinese Journal of Chemical Engineering, 2014, 22(7):774-781.

[12] COPP D A, HESPANHA J P. Simultaneous nonlinear model predictive control and state estimation[J]. Automatica, 2017, 77:143-154.

[13] 王超,张胜修,郑建飞, 等.基于气动特性辨识的飞行器抗饱和自适应控制[J]. 航空学报, 2013, 34(12): 2645-2657.

WANG C, ZHANG S X, ZHENG J F, et al. The anti-windup adaptive control of aircraft based on online identification of aerodynamic characteristics[J]. Acta Aeronoutica et Astronautica Sinica, 2013, 34(12): 2645-2657.

[14] OJAGHI P, BIGDELI N, RAHMANI M. An LMI approach to robust model predictive control of nonlinear systems with state-dependent uncertainties[J]. Journal of Process Control, 2016, 47:1-10.

[15] PETKAR S J, GUPTA A A, KETKAR V D, et al. Robust model predictive control of PVTOL aircraft[J]. IFAC Papersonline, 2016, 49(1):760-765.

[16] MURILLO M, SNCHEZ G, GIOVANINI L. Iterated non-linear model predictive control based on tubes and contractive constraints[J]. ISA Transactions, 2016, 62:120-128.

[17] 程士广, 姜长生, 吴庆宪. 基于模糊干扰观测器的无人机自主着陆逆控制器设计[J]. 电光与控制, 2012, 19(11): 17-20.

CHENG S G, JIANG C S, WU Q X. Design of a dynamic inversion flight controller for UAV landing based on fuzzy disturbance observer[J].Electronics Optics & Control,2012,19(11): 17-20.

[18] KIM E. A discrete-time fuzzy disturbance observer and its application to control[J]. IEEE Trans.on Fuzzy Systems, 2003, 11(3): 399-410.

[19] 王超,张胜修,秦伟伟.具有自适应噪声边界的Tube可达集鲁棒预测控制[J]. 控制理论与应用, 2014, 30(1): 11-18.

WANG C, ZHANG S X, QIN W W. Tube-reachable set based robust model predictive control with adaptive disturbances boundaries[J].Control Theory & Applications,2014,30(1):11-18.

[20] 曹立佳,张胜修,刘毅男,等. 带有自适应参数近似的块控反步飞行控制器设计[J]. 航空学报. 2011, 32(12): 2259-2267.

CAO L J, ZHANG S X, LIU Y N. Flight controller design using adaptive parameter approximation block backstepping[J]. Acta Aeronoutica et Astronautica Sinica, 2011, 32(12): 2259-2267.

[21] 刘毅男,张胜修,曹立佳,等.基于气动特性辨识的折叠翼飞行器可重构控制系统设计[J].系统工程与电子技术,2013,35(5):1037-1044.

LIU Y N, ZHANG S X, CAO L J. Reconfigurable flight control system design for folding-wing air vehicles based on aerodynamic characteristics identification[J]. Systems Engineering and Electronics, 2013, 35(5):1037-1044.