基于改进DE算法的敏捷成像卫星前摄式调度

李志亮, 李小将, 张东来

(1. 航天工程大学研究生院, 北京 101416; 2. 航天工程大学宇航科学与技术系, 北京 101416; 3. 酒泉卫星发射中心, 甘肃 酒泉 732750)

0 引 言

敏捷成像卫星与传统成像卫星相比具有滚动、俯仰和偏航姿态机动性能,对地观测能力更强,任务冲突的解决方式更多,已成为新型卫星发展的重要方向[1]。有效的规划和调度是敏捷成像卫星发挥其优势的重要支撑,也是国内外学者研究的热点问题。目前,多数研究[1-4]在确定条件下展开,即假设与调度相关的信息都是确定的。然而不确定因素在敏捷成像卫星任务调度中时刻存在,并且影响调度方案的执行。文献[5]总结了4种典型的不确定因素,包括新任务的到达、目标观测和数传机会的变化、卫星资源状态的不确定性、任务属性的变化。为应对不确定因素的影响,许多学者研究了前摄式调度方法,前摄式调度[6]是指在调度之初预先考虑不确定因素,将其作为先验知识引进调度中,生成适应性或鲁棒性调度方案。有效地表示不确定因素并构建鲁棒性指标是建立前摄式调度鲁棒模型的关键。文献[7]基于随机云层预测模型研究了EO-1卫星的鲁棒性规划问题。文献[8]针对云层覆盖的不确定因素,提出一种基于邻域的鲁棒性指标,建立了约束满足模型并采用基于分级优化策略的随机变邻域禁忌搜索算法进行求解。文献[9]在文献[8]基础上,增加了总任务执行时间指标,建立了多目标鲁棒调度模型,采用NSGA-Ⅱ算法求解。文献[10]将总时间重叠度和总任务执行时间作为鲁棒性指标,建立了多目标鲁棒性模型,同样采用NSGA-Ⅱ算法求解。文献[11]考虑将任务调度到多个可见窗口以增加观测成功的概率,构建了鲁棒模型。文献[12]考虑任务间卫星姿态转换约束和重要时间窗预留规则,提出一种基于资源预留的鲁棒性任务规划方法。

上述研究中,文献[7-12]均没有考虑卫星资源失效对调度的影响,不能满足卫星资源状态不确定条件下调度系统具有较强鲁棒性的需求。此外,观测任务的选择、排序以及观测时间的确定增加敏捷成像卫星前摄式调度求解的复杂性,传统求解算法[9-10]难以适用。

针对以往研究的不足,本文考虑卫星资源失效、应急任务加入两类不确定因素,构建了期望收益和松弛时间两个鲁棒性指标,将这两类指标作为优化目标构建了前摄式调度鲁棒模型,针对该模型的多目标优化特性,设计了一种多目标离散差分进化求解算法。并通过仿真计算验证了算法的优越性。

1 前摄式调度鲁棒模型

敏捷成像卫星观测任务的执行伴随着两类主要的不确定因素:卫星资源失效和应急任务加入。前摄式调度是应对不确定因素的重要方法,敏捷成像卫星前摄式调度是指将卫星资源失效概率、任务执行主从窗口等信息作为先验知识,构建兼顾收益和鲁棒性的优化目标,同时结合卫星资源和任务执行约束条件,将有限的卫星资源分配给多个观测任务,并确定任务执行时间,生成鲁棒性调度方案。本文首先构建期望收益、松弛时间两个鲁棒性指标,进而建立前摄式调度鲁棒模型。

1.1 鲁棒性指标构建

本文考虑的鲁棒性指标包括期望收益和松弛时间。

1.1.1 期望收益

卫星资源失效具有很强的随机性,其发生难以预测。文献[13]假设某一时刻至多一颗卫星失效,且失效事件相互独立,但是没有给出失效概率计算方法。文献[14]假设机器故障概率与工作时间呈正相关,对机器故障概率进行了描述。借鉴该描述,本文增加空闲时间失效概率,假设卫星资源失效满足指数分布,采用下式计算卫星失效概率:

(1)

式中,pn(t)表示t时刻卫星sn失效的概率;rth表示卫星sn第h次失效后维修结束时间,且rth≥0,调度初始时刻,记rth=0；FTl表示卫星sn在[rth,t]内的第l个空闲时间段;tsFTl和teFTl表示该时间段的起止时间;NFT表示[rth,t]内空闲时间段的数量;AWTn表示卫星sn的平均正常工作时间;ARTn表示卫星sn的平均维修时间。

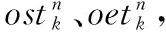
(2)

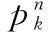
考虑了卫星资源失效的概率,以及任务执行的潜在可用从窗口,本文采用下式表示任务ti的期望收益:

(3)

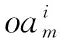
1.1.2 松弛时间

研究表明调度方案中预留松弛时间能够吸收任务变化带来的扰动,增强调度的鲁棒性[15]。借鉴文献[15]对松弛时间的定义,本文将敏捷成像卫星前摄式调度中的松弛时间定义为:设任务ti、tj为相邻任务,松弛时间是指从任务ti到tj的姿态转换结束到任务tj开始观测的时间段,描述如下式:

slackij=otj-oti-di-trij-tst

(4)

式中,oti、otj分别表示ti、tj的开始观测时间;di表示ti的观测时长;trij表示卫星从ti到tj的姿态机动时间;tst表示卫星姿态机动稳定时间。

1.2 鲁棒模型描述

本文在敏捷成像卫星调度领域经典文献[1]的基础上进行合理扩展,考虑多颗卫星多个轨道圈次、任务间姿态转换、以及星上存储和能量等现实条件,从以下4个方面描述模型。

1.2.1 参数定义

本文模型相关参数定义如表1所示。

表1 相关参数定义

1.2.2 决策变量

本文采用的决策变量包括两个:任务ti是否被观测,任务ti和tj是否为相邻任务,描述如下式:

(6)

1.2.3 目标函数

根据文中提出的期望收益和松弛时间指标,敏捷成像卫星前摄式调度鲁棒模型的优化目标为最大化调度期望收益和总松弛时间,其表达式为

(7)

(8)

式中,F1表示最大化调度期望收益;F2表示最大化总松弛时间。

1.2.4 约束条件

考虑任务间姿态转换约束、星上存储和能量约束等,本文模型包括以下5方面的约束条件:

(1) 任务执行的唯一性约束

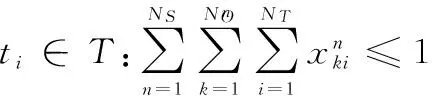
(9)

(10)

(2) 任务执行的时间窗口约束

(11)

(3) 相邻任务间姿态转换时间约束

∀ti,tj∈T,i≠j:

(12)

(4) 卫星单个轨道圈次的存储约束

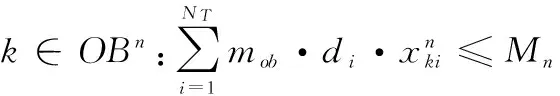
(13)

(5) 卫星单个轨道圈次的能量约束

∀sn∈S,∀k∈OBn,∀ti,tj∈T,i≠j:

(14)

上述模型将调度期望收益和总松弛时间作为优化目标,同时考虑了卫星资源和观测任务的多重复杂约束,是较为复杂的多目标优化模型,本文采用多目标离散差分进化算法进行求解。

2 MDDE求解算法

敏捷成像卫星前摄式调度鲁棒模型的求解是一个多目标优化问题。NSGA-Ⅱ算法在多目标优化上取得了不错的效果[9,16],同时,NSGA-Ⅱ算法在寻优中容易陷入局部最优,而且基于拥挤距离的多样性评价准则没有考虑目标函数值阶数的差别,容易出现多个解聚集的情况。本文考虑差分进化的全局探索优势[17]和扰动操作的局部搜索能力,从离散差分进化、外部存档更新策略、Pareto解集的评价方面设计MDDE求解算法,并给出了算法的实现步骤。

2.1 离散差分进化设计

离散差分进化基本思路是首先采用离散形式对解进行编码,然后生成算法的初始种群,进而采用变异、交叉、选择算子得到下一代个体,通过竞争获得解空间内更好的解。

解的编码和初始种群生成是离散差分进化的基础。对于解的编码,本文根据任务执行顺序采用自然数编码方式,建立卫星与任务的对应关系,例如,x=[3 5 1 0 2 4 9 0 6 8 7],其中数字0用以区分不同的卫星。对于初始种群的生成,本文在贪婪算法[1]的基础上,增加两个随机因素:随机选择卫星轨道圈次、轮盘赌法选择候选任务,采用随机贪婪算法(random greedy algorithm,RGA)生成规模为NP的初始种群。

2.1.1 变异算子

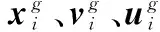
(15)

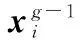
对于变异个体的产生,DesCons[18]、InsertMut[19]等操作取得了不错的寻优效果,但是这些操作所针对的调度问题没有任务执行的时间窗口约束,不能被本文直接采用。因此,本文提出适用于敏捷成像卫星调度问题的DC操作和F操作。

DC操作的基本思路是首先从每颗卫星的任务序列中随机删除比例为dps的任务,dps∈(0,1),然后从未安排的任务集合中随机选择比例为cps的任务,将选择的任务按照调度约束条件插入到现有序列中,得到变异个体。

F操作的基本思路是判断相邻任务间的松弛时间是否大于阈值MinD·slc,MinD表示所有任务的最小观测时长,slc表示扰动强度,slc∈[1,10],如果小于MinD·slc,则删除相邻任务中wi/di较小的任务,得到变异个体。

2.1.2 交叉算子

根据离散差分进化的机理,试验个体可采用下式获得[19]:

(16)

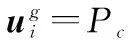
基于块结构的整体移动策略[19]是一种有效的试验个体产生操作。在敏捷成像卫星调度问题中,由于时间窗口约束,任务序列同样具有块结构特征,但是块结构的整体移动容易产生不可行解。为此,本文提出一种考虑局部修复的CR操作,基本思路是对于每颗卫星的任务序列,随机选择一个切点,计算切点处任务的观测结束时间,将满足姿态转换的切点右侧任务序列进行交换,然后删除交换后任务序列中重复的任务,得到试验个体。

2.1.3 选择算子

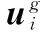
(17)

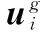
2.2 外部存档更新策略

为保留算法进化中优质解,本文采用外部存档保存搜索到的非支配解,设外部存档为EA,EA={ea1,ea2,…,eaNE},NE表示EA的规模,每进化一代,EA根据当前新解y进行更新。同时,为避免EA中非支配解过于集中,引进个体间的归一化邻域距离,当EA的规模大于NP时,根据归一化邻域距离删除拥挤的解,以保持解的多样性。

对于两个目标函数的多目标优化问题,设两个目标函数分别为f1(·)和f2(·),根据Pareto解集的定义,EA中任意两个解互相不构成支配关系,即对于∀eak,eak+1∈EA,若f1(eak)f2(eak+1),因此将EA中所有解按照f1(·)函数值升序排列时,其f2(·)函数值为降序排列。y与EA的相对关系如图1所示。

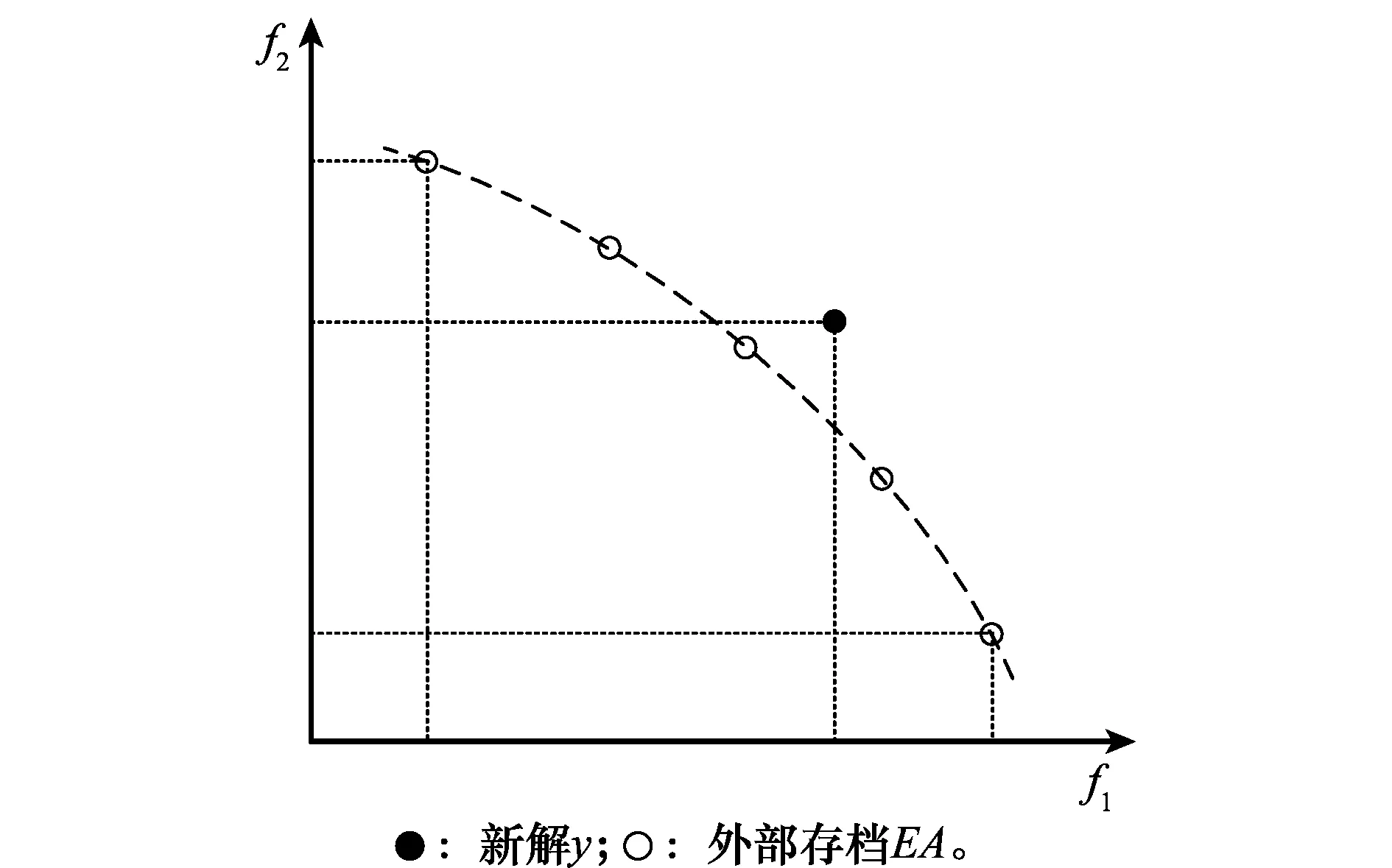
图1 新解y与外部存档EA的相对关系Fig.1 Relative relationship between new solution y and external archive EA

由图1可知,EA的更新包括4种情况:①当y与EA的每个解均互不支配时,将y加入EA;②当y支配EA的部分解时,将被支配的解从EA删除,并将y加入EA;③当y支配EA的全部解时,将EA的所有解删除,并将y加入EA;④当y被EA的任一解支配时,则不更新EA。

为保持EA中非支配解的多样性,需量化评价解之间的拥挤程度,文献[16]提出一种拥挤距离计算公式,该公式具有简单高效的计算特点,但是没有考虑目标函数值阶数的差别,容易出现多个解聚集的情况。为此,本文在计算相邻解的距离时对目标函数值进行归一化处理,称之为归一化邻域距离,其计算公式为

(18)

当外部存档超过一定规模时,需根据归一化邻域距离计算出外部存档中最拥挤的解,将EA中所有解的归一化邻域距离记为集合ND,ND={nd1,nd2,…,ndNE-1},设ND中最小的距离为ndk,比较ndk左侧和右侧的邻域,若ndk-1ndk+1,则eak+1为最拥挤的解,若ndk-1=ndk+1,则需进一步向两侧扩展,直至确定最拥挤的解,并将最拥挤的解从外部存档删除。

2.3 Pareto解集的评价

MDDE算法的求解过程就是不断构造Pareto解集,并向解空间的最优前沿靠近的过程。因此,对多目标差分进化算法性能评价的重要依据是Pareto解集的优劣。不同于单目标优化,多目标优化很难用单一的指标来衡量,通常会考虑3方面的性能指标[20]:收敛性、均匀性和多样性。针对这3方面的性能指标,本文结合敏捷成像卫星前摄式调度的特点,对文献[20]提出的指标进行了改进,采用以下3个量化指标对Pareto解集进行评价,这里记待评价的Pareto解集为SP,其规模为NS,初始种群的非劣解集为InitS。

2.3.1 世代距离

世代距离[20](generational distance,GD)用于评价求解所得Pareto解集与真实Pareto最优解集的接近程度,该指标需要参考Pareto最优解集才能确定,而现实中调度问题解空间的最优解集难以获得。本文将初始种群的非劣解集作为参考集合以评价Pareto解集的收敛性,GD计算公式为

(19)

(20)

式中,rdk为非支配解xk(xk∈SP)到InitS的最小欧式距离;GD表示SP相对InitS的进化距离,与文献[20]不同,本文中GD越大,SP越接近Pareto最优前沿;当GD=0时,SP即为InitS。

2.3.2 分散间距

分散间距(spacing,SP)[20]用于评价Pareto解集中各个解分布的均匀性和多样性,与文献[20]不同的是,本文考虑目标函数值阶数的差别,采用归一化邻域距离计算相邻解之间的距离,SP计算公式为

(21)

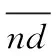
2.3.3 最大分布广度

最大分布广度(maximum spread,MS)[20]用于衡量Pareto解集的散布范围,本文在MS的计算时将初始解集的非劣解集作为参考集合,计算公式为

(22)

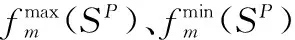
2.4 算法实现步骤

综合上述的分析和设计,MDDE算法实现的具体步骤如下:

步骤1初始化算法的相关参数:种群规模NP、最大迭代次数Itermax、变异概率Pm、交叉概率Pc;采用随机贪婪算法生成初始种群。

步骤2对初始种群进行基于Pareto的非支配排序,将排序后初始种群的最优前沿作为外部存档EA。

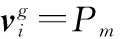
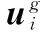
步骤5判断是否达到最大迭代次数Itermax,如果达到,则输出外部存档EA作为Pareto非劣解集,并对解集的收敛性、均匀性、多样性进行评价,如果没有达到,则重复步骤步骤3和步骤4。

3 仿真验证

首先设置敏捷成像卫星、成像任务和MDDE算法的相关参数,然后采用Matlab R2010b实现MDDE算法,并对比分析MDDE与NSGA-Ⅱ[9,16]算法的求解结果。

3.1 参数设置

仿真算例中敏捷成像卫星的主要参数参考Pleiades卫星[1],成像任务采取随机生成的方式获得,考虑到点目标是成像的基本单元,条带目标可以看作具有一定观测时长的点目标,区域目标通过分解可由点目标和条带目标组成,本文选择在一定范围内随机生成不同规模的点目标任务集[21]。卫星和任务的主要参数如表2所示。

表2 卫星和任务的主要参数

表2中,rand([x,y])表示x和y之间服从均匀分布的随机数。通过组合产生5组算例(卫星数～任务数):2～50、3～100、4～200、5～300、6～600。

算法参数设置如下:种群规模NP=100,进化代数Itermax=100,变异概率Pm=0.7,交叉概率Pc=0.5,解构的扰动强度dps=0.4,重构的扰动强度cps=0.6,插入松弛时间的扰动强度slc=2。

3.2 算法实现与结果分析

采用Matlab实现MDDE算法,计算机配置为Intel Core i7-3770 CPU @3.4GHz、8核4GB内存,操作系统为Windows 7、编程环境为Matlab R2010b。为验证MDDE的优越性,将MDDE与NSGA-Ⅱ算法[9,16]在5组算例上进行对比,以世代距离、分散间距、最大分布广度作为算法性能对比的指标,需要说明的是,这3个指标均无量纲。为避免随机因素的影响,每种算法在每组算例上独立运行20次并取平均值,对比如表3所示。

表3 MDDE与NSGA-Ⅱ算法的性能对比

由表3可知,在GD指标上,MDDE比NSGA-Ⅱ高14.32%左右,说明MDDE算法求解得到的Pareto解集更接近真实最优前沿;在SP指标上,MDDE比NSGA-Ⅱ低5.17%左右,说明MDDE算法求解得到的Pareto解集中各个解的分布更均匀;在MS指标上,MDDE比NSGA-Ⅱ高11.79%左右,说明MDDE算法求解得到的Pareto解集的最大分布范围更广。

以算例4～200为例,MDDE与NSGA-Ⅱ算法的Pareto求解结果对比如图2所示。图2中,RGA表示采用随机贪婪算法求解得到的初始种群非劣解集,NSGA-Ⅱ-100表示采用NSGA-Ⅱ算法迭代100次求解得到的Pareto解集,MDDE-1、MDDE-50、MDDE-100分别表示采用MDDE算法迭代1、50、100次求解得到的Pareto解集。

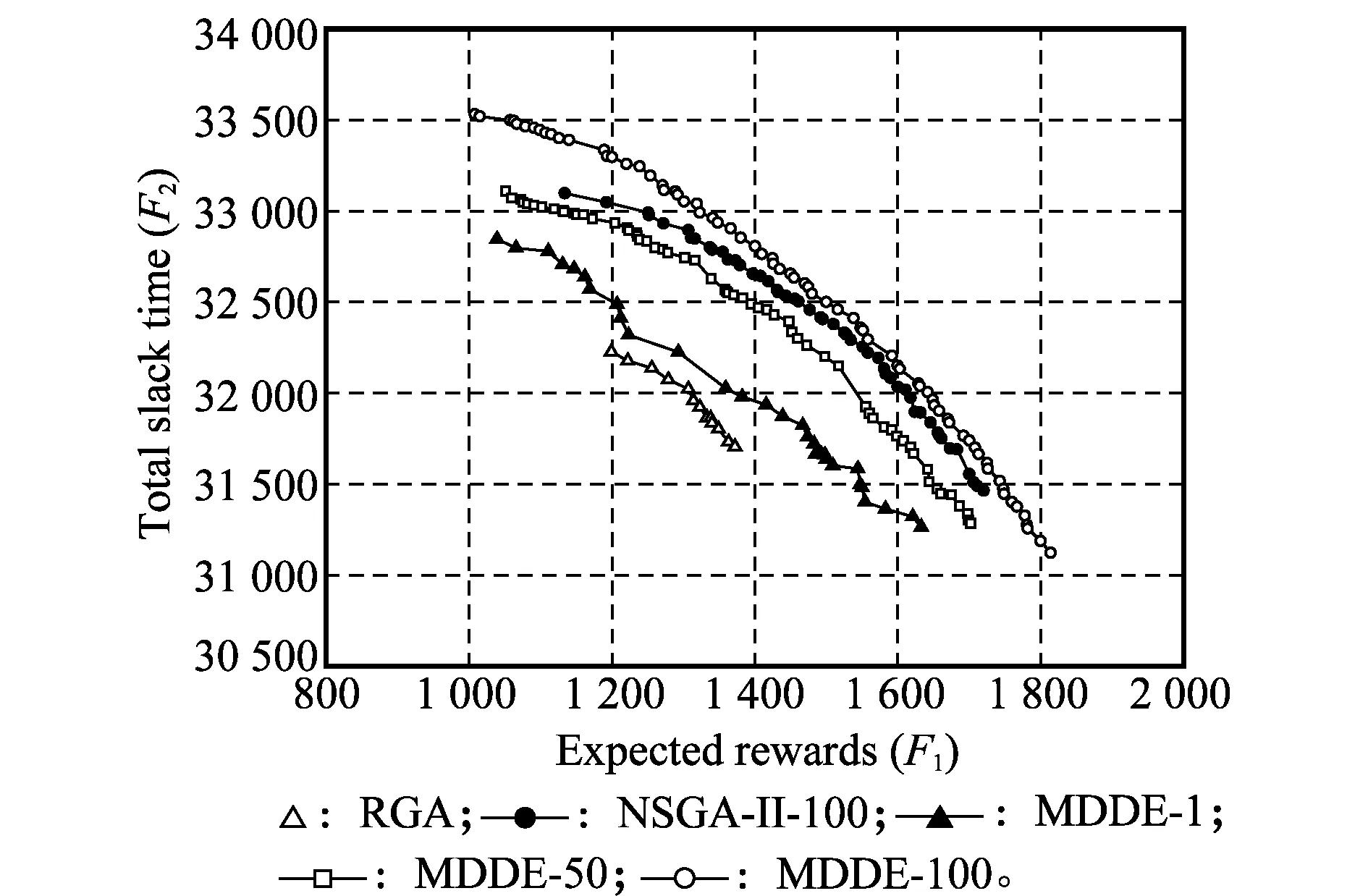
图2 MDDE与NSGA-Ⅱ算法Pareto求解结果对比Fig.2 Pareto solution comparison of MDDE with NSGA-Ⅱ algorithm

由图2可知,MDDE算法从初始种群开始,通过多次迭代,不断向解空间最优前沿靠近,且MDDE算法经过100次迭代求解所得解集优于NSGA-Ⅱ算法经过100次迭代求解所得解集。

在运行时间方面,MDDE与NSGA-Ⅱ算法在5个算例上的结果对比如图3所示。由图3可知,MDDE的运行时间在5个算例上比NSGA-Ⅱ平均降低了9.72%左右,说明MDDE比NSGA-Ⅱ的求解效率更高。同时可以看出,从算例2～50到6～600,随着算例规模的变大,算法的运行时间大幅增长,这是由于敏捷成像卫星前摄式调度问题具有NP-Hard特性,解空间随问题规模呈指数级增大,算法运行时间也大幅增长。

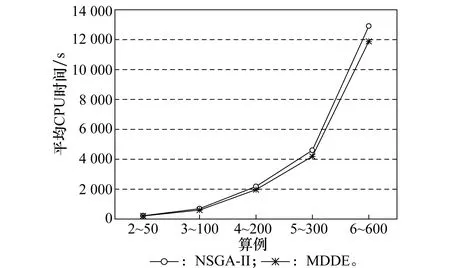
图3 MDDE与NSGA-Ⅱ算法运行时间对比Fig.3 Average CPU time comparison of MDDE and NSGA-Ⅱ algorithm

综上结果分析,MDDE算法在求解结果和求解效率上均优于NSGA-Ⅱ算法,验证了MDDE算法的优越性。

4 结 论

本文针对敏捷成像卫星前摄式调度中存在的卫星资源失效、应急任务加入两类不确定因素,构建了以期望收益和松弛时间为优化目标的调度鲁棒模型,针对该模型的多目标优化特性,提出了一种MDDE求解算法,仿真结果表明3个Pareto解集评价指标上MDDE比NSGA-Ⅱ提高了10.42%左右,在运行时间上降低了9.72%左右,验证了MDDE算法的优越性。同时,本文研究没有考虑扰动事件发生后如何对方案进行调整,在后续工作中,可进一步研究反应式调度模型和算法,以期采用较小幅度的方案调整应对多种扰动事件的影响。

[2] HABET D, VASQUEZ M, VIMONT Y. Bounding the optimum for the problem of scheduling the photographs of an agile earth observing satellite[J]. Computational Optimization and Applications, 2010, 47(2): 307-333.

[3] 姜维, 庞秀丽, 郝会成. 成像卫星协同任务规划模型与算法[J]. 系统工程与电技术, 2013, 35(10): 2093-2101.

JIANG W, PANG X L, HAO H C. Collaborative scheduling model and algorithm for imaging satellite network[J]. Systems Engineering and Electronics, 2013, 35(10): 2093-2101.

[4] XU R, CHEN H, LIANG X, et al. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization[J]. Expert Systems with Applications, 2016, 51(C): 195-206.

[5] PEMBERTON J C, GREENWALD L G. On the need for dynamic scheduling of imaging satellites[J]. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 2002, 34(1): 165-171.

[6] LAMBRECHTS O, DEMEULEMEESTER E, HERROELEN W. Proactive and reactive strategies for resource-constrained project scheduling with uncertain resource availabilities[J]. Journal of Scheduling, 2008, 11(2): 121-136.

[7] ABRAMSON M, CARR F, CARR D, et al. Robust planning for the Earth Observing-1 (EO-1) mission[C]∥Proc.of the AIAA Aerospace Conference, 2013: 33-36.

[8] 王军民,李菊芳,谭跃进.不确定条件下卫星鲁棒性调度问题[J].系统工程,2007,25(12): 94-99.

WANG J M, LI J F, TAN Y J. The robust satellite scheduling problem under uncertainty[J].Systems Engineering,2007,25(12): 94-99.

[9] NIU X, TANG H, WU L, et al. Imaging-duration embedded dynamic scheduling of earth observation satellites for emergent events[J].Mathematical Problems in Engineering,2015,4:1-31.

[10] 邓润, 唐宏, 单越, 等. 面向应急任务卫星鲁棒性规划模型及算法[J]. 遥感信息, 2014, 29(5): 25-31.

DENG R, TANG H, SHAN Y, et al. Emergency task oriented satellite robust mission planning model and algorithm[J]. Remote Sensing Information, 2014, 29(5): 25-31.

[11] WANG J, DEMEULEMEESTER E, QIU D. A pure proactive scheduling algorithm for multiple earth observation satellites under uncertainties of clouds[J]. Computers & Operations Research, 2016,74(C):1-13.

[12] 张忠山, 谭跃进, 义余江, 等. 基于资源预留的成像卫星鲁棒性任务规划方法[J]. 系统工程理论与实践, 2016, 36(6): 1544-1554.

ZHANG Z S, TAN Y J, YI Y J, et al. A robustness task planning method for imaging satellite based on resources reservation[J]. Systems Engineering Theory & Practice, 2016, 36(6): 1544-1554.

[13] ZHU X, WANG J, QIN X, et al. Fault-tolerant scheduling for real-time tasks on multiple earth observation satellites[J]. IEEE Trans.on Parallel & Distributed Systems, 2014, 26(1): 1-15.

[14] 何伟. 机器故障下柔性Job Shop调度研究[D]. 重庆: 重庆大学, 2012.

HE W. Study on flexible job shop scheduling with machine breakdown[D]. Chongqing: Chongqing University, 2012.

[15] DAVENPORT A J, BECK J C. Slack-based techniques for robust schedules[C]∥Proc.of the 6th European Conference on Planning, 2001: 43-49.

[16] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans.on Evolutionary Computation, 2002, 6(2): 182-197.

[17] STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 1(4): 341-359.

[18] TASGETIREN M F, SUGANTHAN P N, PAN Q K. An ensemble of discrete differential evolution algorithms for solving the generalized traveling salesman problem[J]. Applied Mathematics and Computation, 2010, 215(9): 3356-3368.

[19] PAN Q K, TASGETIREN M F, LIANG Y C. A discrete differential evolution algorithm for the permutation flow shop scheduling problem[J]. Computers & Industrial Engineering, 2008, 55(4): 795-816.

[20] ZITZLER E, DEB K, THIELE L. Comparison of multi-objective evolutionary algorithms: empirical results[J]. Evolutionary Computation, 2000, 8(2): 173-195.

[21] 李志亮, 李小将, 孙伟. 考虑成像质量的敏捷卫星任务调度模型与算法[J]. 宇航学报, 2017, 38(6): 590-597.

LI Z L, LI X J, SUN W. Task scheduling model and algorithm for agile satellite considering imaging quality[J]. Journal of Astronautics, 2017, 38(6): 590-597.