基于椭圆-双曲线马氏度量的图像分类算法

鲍文霞, 阎少梅, 梁 栋, 胡根生

(1. 安徽大学计算机智能与信号处理教育部重点实验室, 安徽 合肥 230039; 2. 偏振光成像探测技术安徽省重点实验室, 安徽 合肥 230031)

0 引 言

图像分类作为图像理解的基础,是计算机视觉和模式识别领域中重要且应用广泛的研究方向之一,如在目标识别[1]、物体检测[2]以及场景识别与分类[3]等方面都有应用。图像分类是利用计算机视觉技术,根据目标在图像信息中所反映出的特征,把不同类别的目标识别、区分开来的图像处理方法[4-9]。目前大部分的图像分类方法都依赖于用图像特征间的距离来度量图像内容的语义相似度,实现对图像内容的理解与分类,因此距离度量在图像分类中扮演了重要的角色,文献[10]提出了k最近邻分类方法,通过度量出与测试样本距离最近的k个训练样本,根据它们的类别来决定测试样本的类别;文献[11]在此基础上提出了基于监督的最近邻分类方法;文献[12]结合贝叶斯分类器和k最近邻分类器提出了一种新的基于距离度量的分类方法。这些算法在度量图像特征间的相似性的时候都采用的是欧氏距离,欧氏距离度量对所有属性特征同等对待,忽略了属性特征间的主次关系,没有突出不同的属性特征对分类带来不同的影响,因此会降低分类器的性能[13]。

目前流行的解决方法是用马氏度量[14]取代欧氏度量,如文献[15]提出的大间隔最近邻分类算法,从局部近邻中学习一个马氏度量距离从而实现分类。马氏度量考虑了数据样本维度分量之间的相关性,即非平等地对待数据样本的各个维度分量,因而在实际应用中比欧氏度量有更好的分类效果。例如,文献[16]提出了基于图像到类距离度量的图像分类方法,该方法基于最近邻原则度量图像间的马氏距离实现分类;文献[17]提出基于马氏距离的高斯概率分布从而实现了信息理论度量学习的分类算法。马氏度量学习是通过训练样本,寻找一种能够反应样本空间结构信息或语义信息的线性变换,虽然马氏度量学习得到的马氏度量优于欧氏度量,但线性变换局限了马氏度量的应用范围。为了进一步拓宽度量学习在图像分类中的适用范围同时提高分类的性能,本文提出基于椭圆-双曲线马氏度量学习的图像分类算法。椭圆-双曲线马氏度量学习问题就是对于给定训练样本数据,寻找一种能够反应样本空间结构信息或语义信息的分式线性变换,从而使得椭圆-双曲线马氏度量有更好区分性。线性变换是分式线性变换的一种特殊形式,因此基于椭圆-双曲线马氏度量学习适用范围更广。基于椭圆-双曲线马氏度量学习的图像分类算法首先提取图像特征,图像特征由HSV(色调Hue, 饱和度Saturation, 亮度Value)与Lab(L(亮度Lightness), a(色度chromaticity,+a表示红色,-a表示绿色), b(色度chromaticity,+b表示黄色,-b表示蓝色))直方图描述的颜色特征和局部二值模式(local binary patterns,LBPs)描述的纹理特征构成;然后根据数据统计特性定义椭圆-双曲线马氏度量,通过椭圆-双曲线马氏度量学习获取最优的度量矩阵;最后通过度量图像特征间的距离实现了图像分类。

1 椭圆-双曲线度量

在数学史上,当欧氏几何学的平行公理被质疑时,两种非欧几何学诞生,即椭圆型几何和双曲线型几何[18]。

给定一个可逆对称矩阵Ω∈R(n+1)×(n+1),它诱导出x,y∈Rn的双线性形式为

∀x,y∈Rn

(1)

下面将ω(x,y)用其简化形式ωxy来表示,其中(xT,1)T表示点x的齐次坐标。根据Ω是正定或者不定,ωxy诱导出两种度量几何,即椭圆型度量和双曲线型度量。如果矩阵Ω是正定的,令En={x∈Rn:ωxx>0},定义ρE:En×En→R+,椭圆型度量为

(2)

式中,i为虚数单位,如果矩阵Ω是不定的,令Hn={x∈Rn:ωxx>0},定义ρE:Hn×Hn→R+,双曲线型度量为

(3)

在En和Hn上,和ρH(x,y)两种ρE(x,y)度量均满足其4个条件,即满足

(4)

因此,ρE(x,y)和ρH(x,y)是En和Hn上的度量,椭圆型度量与双曲线型度量共同构成椭圆-双曲线度量。其中,(En,ρE)叫做椭圆型几何;(Hn,ρH)叫做双曲型几何;1/k是椭圆几何空间的曲率;-1/k是双曲几何空间的曲率。可以将椭圆-双曲线度量表示为

(5)

根据以上定义可知,椭圆-双曲线度量依赖于一个对称矩阵Ω,给定一个对称矩阵就可以确定一个椭圆-双曲线度量。

2 椭圆-双曲线马氏度量

数据的统计特性在一定程度上反映了样本数据的几何结构,因此可以由样本数据的均值和协方差矩阵计算初始椭圆-双曲线度量矩阵。对于给定的样本矩阵

表示第i个样本,1≤i≤N。令Xj=(xj1,xj2,…,xjN),1≤j≤n,且mj为Xj的均值,那么矩阵样本X可以表示为X=(X1,X2,…,Xn)T,于是Xi与Xj的协方差为cov(Xi,Xj)=(Xi-mi)(Xj-mj)T/(N-1)。因此,样本矩阵X的协方差矩阵为

令m=(m1,m2,…,mn)T,则初始椭圆-双曲线度量矩阵定义为

(6)

(xi-m)Tcov-1(xj-m)±k2,k>0

(7)

(9)

已知,样本xi和xj间的马氏距离为

(10)

式中,矩阵G∈Rd×d为样本xi和xj协方差矩阵的逆矩阵,即G=cov(xi,xj)-1。

因此,从几何上可以得到椭圆-双曲线度量与马氏度量的关系为

(11)

式中,1/k(-1/k)是椭圆(双曲线)空间的曲率,在k取极限的情况下椭圆-双曲线度量无限接近马氏度量,因此将由数据统计特性得到的特殊形式的椭圆-双曲线度量称为椭圆-双曲线马氏度量。

3 椭圆-双曲线马氏度量学习

椭圆-双曲线马氏度量学习问题就是对于给定训练样本数据,寻找一个最优的椭圆-双曲线马氏度量矩阵使得相应的度量在某种学习准则下是最优的。根据传统的马氏度量学习常用的大间隔最近邻(large margin nearest neighbor, LMNN )准则[19],可以得到椭圆-双曲线马氏度量学习框架下的LMNN学习准则,简称椭圆双曲线-大间隔最近邻(elliptic hyperbolic-large margin nearest neighbor，EH-LMNN)准则。

由于xi和xj的椭圆-双曲线马氏距离度量为

dEH(xi,xj)=

(12)

因此,椭圆-双曲线马氏度量在EH-LMNN学习准则下的最优化问题可表示为

(13)

式中,xj是xi的目标近邻,记j→i。给定一个二值函数yij∈{0,1}来表示样本xi与样本xj的类标签是否相同,yij=1表示样本xi和xj类别相同,yij=0表示类别不同。xl为不同标签的样本,μ是平衡参数,一般取0.5。ξijl≥0表示标签不同的数据xl侵入由xi的目标近邻xj定义的xi的周围边界的数目,即ξijl≥1+dEH(xi,xj)-dEH(xi,xl)。

M0=LTL

(14)

通过约束条件和铰链函数将松弛变量ξijl表示为L的函数为

ξijl(L)=[1+dEH(xi,xj)-dEH(xi,xl)]+

(15)

式中,如果z≥0,[z]+=z;否则,[z]+=0。

将式(15)考虑进目标函数中,其表达式为

(16)

因此最优化问题可以通过梯度下降法迭代解决,即对式(16)进行求导,记矩阵L在第t次迭代时为Lt,目标函数的梯度函数在度量矩阵第t次迭代时的计算式为

(17)

式(17)中的两部分的导数分别为

(18)

(19)

因此通过梯度下降法迭代收敛后获得最优的变换矩阵L,通过L可以得到椭圆-双曲线度量学习中的最优椭圆-双曲线马氏度量矩阵M=LTL。

学习算法如下:

输入训练样本及其标签

步骤1首先根据样本的统计特性计算样本的均值和协方差矩阵;

步骤2给定步长λ,t=1,由式(6)计算初始度量矩阵M0;

步骤3令Mt=M0,对其进行分解Mt=(Lt)T(Lt);

步骤4计算第t次目标函数的值Ψ(Lt);

步骤5由式(17)～式(19)计算第t次的梯度Γt;

步骤6更新Lt+1=Lt-λ·Γt;

步骤7计算Mt+1=(Lt+1)T(Lt+1);

步骤8计算第t+1次目标函数值Ψ(Lt+1);

步骤9判断‖Ψ(Lt+1)-Ψ(Lt)‖≤10-10,若不满足条件，令t=t+1并重复步骤(5)～步骤(9)直至迭代收敛。

输出最优椭圆-双曲线马氏度量矩阵M。

4 图像分类算法及其实验结果

4.1 图像分类算法流程

基于椭圆-双曲线马氏度量学习的图像分类算法提取图像特征,图像特征由HSV与Lab直方图描述的颜色特征和LBPs描述的纹理特征构成,并采用主成分分析(principal component analysis,PCA)方法对图像特征进行降维;然后,根据第3节的椭圆-双曲线马氏度量学习算法获取最优的椭圆-双曲线马氏度量矩阵;最后,采用得到的椭圆-双曲线马氏度量矩阵将测试样本变换到新的特征空间并降低特征各维度间的相关性,并利用其计算出测试样本与每个类别的距离,将距离最小所对应的类作为测试样本的类别。算法流程如图1所示。

图1 算法流程图Fig.1 Flow chart of algorithm

4.2 实验结果

利用基于椭圆-双曲线马氏度量的图像分类算法(因在EH-LMNN准则下学习,所以称此算法为EH_LMNN算法)进行了大量实验,下面给出LEAR ToyCars数据集[21]和VIPeR数据集[22]上的实验结果,实验中图像采用同样的特征表示,即由HSV与Lab直方图描述的颜色特征和LBPs描述的纹理特征构成。LEAR ToyCars数据集包含了14种不同的玩具车和卡车的256张图像,图2列举了4种不同玩具车的图像,数据集展示了图像在姿势、灯光以及杂乱背景的变化。分别利用本文的EH-LMNN算法、支持向量机(support vector machine，SVM)算法[4]、马氏度量(mahalanobis metric,MAHAL)算法[14]以及信息理论度量学习(information theoretic metric learning，ITML)算法[17]进行在LEAR ToyCars数据集上进行对比实验;同时采用3种不同的初始矩阵即单位矩阵(I)、随机矩阵(R)以及本文的椭圆-双曲线马氏度量矩阵(M),利用本文的算法进行分类实验。图3给出了实验结果的接收器操作特性(receiver operator characteristic, ROC)曲线和等错误率(equal error rate,EER)值。ROC曲线采用假正率和真正率作为横纵坐标,其中,假正率(false positive rate，FPR)为分类器错误预测为正类的负样本占所有负样本的比例,计算公式为FPR=FP/(FP+TN),其中,FP表示负类样本被预测成正类的数目,TN表示负类样本被预测成负类的数目;真正率(true positive rate，TPR)为分类器正确预测为正类的正样本占所有正样本的比例,计算公式为TPR=TP/(TP+FN),其中,TP表示正类样本被预测成正类的数目,FN表示正类样本被预测成负类的数目。理想情况下,TPR应该接近1,且FPR应该接近0;ROC曲线下方的面积越大,则分类器的分类性能越好。EER值是ROC曲线中错分正负样本概率相等的点,这个点就是ROC曲线与ROC空间中对角线([0,1]-[1,0]连线)的交点。

图3 ROC曲线对比Fig.3 ROC curves comparison

表1和表2分别给出了分类的曲线下方面积(area under curve,AUC)值和正确率。AUC表示ROC曲线下方的面积,面积越大表示分类性能越好。正确率就是被预测正确的样本数除以所有的样本数,即实际正(负)样本被预测正确的概率。

表1 不同算法的AUC值比较

表2 不同算法的正确率比较

由图3、表1及表2实验结果可知,本文基于椭圆-双曲线马氏度量学习的图像分类算法与其他算法相比取得了更好的图像分类性能;并且以椭圆-双曲线马氏度量矩阵M为初始矩阵的分类算法分类效果最佳。

分别利用本文的EH-LMNN算法、SVM算法[4]、MAHAL算法[14]、ITML算法[17]、KISS度量(KISS metric，KISSME)算法[23]以及跨视角二次判别分析(cross-view quadratic discriminant analysis,XQDA)算法[24]在VIPeR数据集上进行对比实验(见表3);其中,图像采用同样的特征表示,即由HSV与Lab直方图描述的颜色特征和LBPs描述的纹理特征构成。VIPeR数据集包含了两个不同相机视角获得的室外632个行人对。其低分辨率图像在姿势、角度上展示出了巨大的变化,同时在高光或者阴影等光照上也有巨大的变化。图4给出两个相机获取的行人图像，大部分的图像对行人的拍摄角度都有90°的变化,这使得分类更具挑战性。实验将632个行人对随机分成两部分,其中316个行人对用于实验训练,剩下的用于实验测试。

表3 在VIPeR数据集行人对的匹配率对比

图4 VIPeR数据集上的行人对实例Fig.4 Pedestrian pairs example on VIPeR dataset

实验将EH_LMNN算法、ITML算法、MAHAL算法、KISSME算法以及XQDA算法进行分类性能的对比,图5给出了实验结果的累计匹配特征(cumulative matching characteristic,CMC)曲线,CMC曲线表示测试集中所选测试图与目标图第n次即成功匹配的概率,其中横坐标表示匹配的次数,纵坐标表示图像的匹配概率。为了实验结果的有效性,取100次实验的平均值。表3具体给出了在第55次、60次、75次以及90次行人对匹配成功的匹配率。

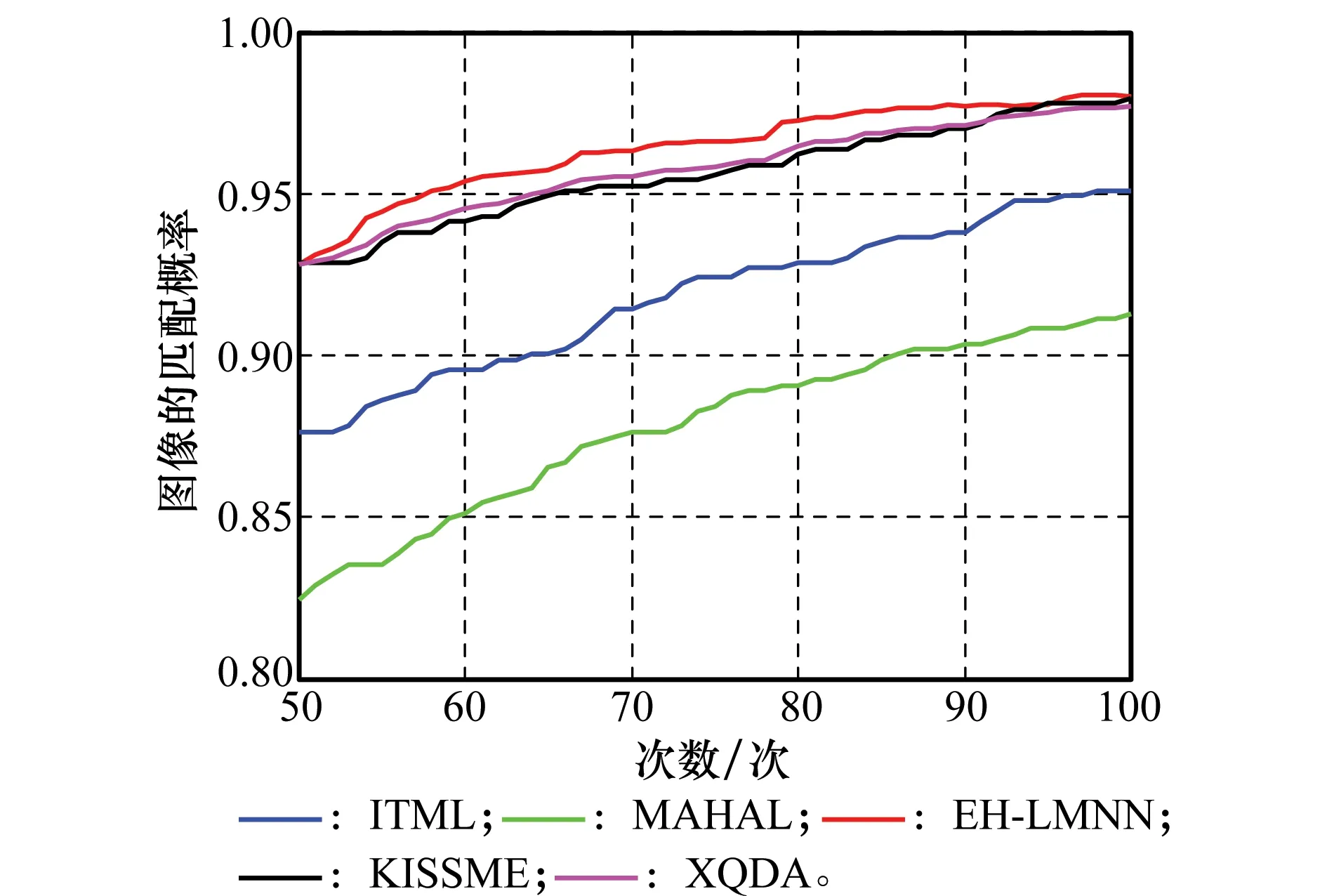
图5 CMC曲线对比Fig.5 CMC curves comparison

由图5和表3的实验结果可以看出,本文基于椭圆-双曲线马氏度量学习的图像分类算法性能优于马氏度量学习,具有更好的适用性。

5 结 论

针对图像分类中的度量学习问题,提出一种基于椭圆-双曲线马氏度量学习的图像分类算法。该算法结合数据点的统计特性定义了椭圆-双曲线马氏度量,建立了椭圆-双曲线马氏度量学习算法,通过度量图像特征间的距离实现了图像分类。实验验证基于椭圆-双曲线马氏度量学习图像分类性能优于传统的马氏度量学习算法。

[1] LIANG M, HU X. Recurrent convolutional neural network for object recognition[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 3367-3375.

[2] ACHANTA R, HEMAMI S, ESTRADA F, et al. Frequency-tuned salient region detection[C]∥Proc.of the 22nd IEEE Internet Conference on Computer Vision and Pattern Recognition, 2009: 1597-1604.

[3] 顾广华,韩晰瑛,陈春霞,等. 图像场景语义分类研究进展综述[J]. 系统工程与电子技术, 2016, 38(4): 938-948.

GU G H, HAN X Y, CHEN C X, et al. Survey on semantic scene classification research[J]. Systems Engineering and Electronics, 2016, 38(4): 938-948.

[4] ENGEL C, BAUMGARTNER P, HOLZMANN M, et al. Person re-identification by support vector ranking[C]∥Proc.of the Conference on British Machine Vision, 2010: 1-11.

[5] 陈善学, 屈龙瑶, 胡灿. 基于空间约束加权条件稀疏表示高光谱图像分类[J]. 系统工程与电子技术, 2016, 38(2): 442-449.

CHEN S X, QU L Y, HU C. Spatial correlation constrained weighted conditional sparse representation for hyperspectral image classification[J]. Systems Engineering and Electronics, 2016, 38(2): 442-449.

[6] SCHMIDHUBER J, MEIER U, CIRESAN D. Multicolumn deep neural networks for image classification[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition, 2012: 3642-3649.

[7] LU J L, WANG G, DENG W H, et al. Multimanifold deep metric learning for image set classification[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 1137-1145.

[8] HU J L, LU J W, TAN Y P. Discriminative deep metric learning for face verification in the wild[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition, 2014: 1875-1882.

[9] LUO Y, LIU T, TAO D, et al. Decomposition-based transfer distance metric learning for image classification[J]. IEEE Trans.on Image Processing, 2014, 23(9): 3789-3801.

[10] COVER T M, HART P E. Nearest neighbor pattern classification[J].IEEE Trans.on Information Theory,1967,13(1):21-27.

[11] WOHLHART P, KOSTINGER M, DONOSER M, et al. Optimizing 1 nearest prototype classifiers[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Rocognition, 2013: 460-467.

[12] FERDOUSY E Z, ISLAM M, MATIN M A. Combination of Naïve Bayes classifier and K-nearest neighbor (cNK) in the classification based predictive models[J]. Computer & Information Science, 2013, 6(3): 48-56.

[13] 杨柳, 于剑, 景丽萍.一种自适应的大间隔近邻分类算法[J]. 计算机研究与发展, 2013, 50(11): 2269-2277.

YANG L, YU J, JING L P. An adaptive large margin nearest neighbor classification algorithm[J]. Journal of Computer Research and Development, 2013, 50(11): 2269-2277.

[14] AHARON B H, TOMER H, NOAM S, et al. Leaning a mahalanobis metric from equivalence constraints[J]. Journal of Machine Learning Research, 2005, 6(6): 937-965.

[15] WEINBERGER K Q, SAUL L K. Fast solvers and efficient implementations for distance metric learning[C]∥Proc.of the 25th Internet Conference on Machine Learning,2008:1160-1167.

[16] WANG Z, HU Y, CHIA L T. Image-to-class distance metric learning for image classification[C]∥Proc.of the European Conference on Computer Vision, 2010: 709-719.

[17] DAVIS J V, KULIS B, JAIN P, et al. Information theoretic metric learning[C]∥Proc.of the 24th Internet Conference on Machine Learning, 2007: 209-216.

[18] RICHTER-GEBERT J. Perspectives on projective geometry: a guided tour through real and complex geometry[M]. USA:Springer, 2011.

[19] NIELSEN F, MUZELLEC B, NOCK R. Classification with mixtures of curved mahalanobis metrics[C]∥Proc.of the IEEE International Conference on Image Processing, 2016: 241-245.

[20] DERENIOWSKI D, KUBALE M. Cholesky factorization of matrices in parallel and ranking of graphs[C]∥Proc.of the 5th International Conference on Parallel Processing and Applied Mathematics, 2003: 985-992.

[21] NOWAK E, JURIE F. Learning visual similarity measures for comparing never seen objects[C]∥Proc.of the IEEE Internet Conference on Computer Vision and Pattern Recognition,2007:1-8.

[22] GRAY D, BRENNAN S, TAO H. Evaluating appearance models for recongnition, reacquisition and tracking[C]∥Proc.of the IEEE Internet Workshop on Performance Evaluation of Tracking and Surveillance, 2007: 2-6.

[23] KOSTINGER M, HIRZER M, WOHLHART P, et al. Large scale metric learning from equivalence constraints[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition, 2012: 2288-2295.

[24] LIAO S C, HU Y, ZHU X Y, et al. Person re-identification by local maximal occurrence representation and metric learning[C]∥Proc.of the IEEE International Conference on Computer Vision and Pattern Recognition, 2015: 2197-2206.