基于多目标演化的模糊认知图学习算法
方 伟, 张龄之
(江南大学物联网工程学院, 江苏 无锡 214122)
0 引 言
认知图是计算智能领域的一个新兴的研究热点,它提供了一个有效的软计算工具来支持基于先验知识的自适应行为[1]。文献[2]在古典认知图的基础之上,融合认知图论和模糊集理论,提出模糊认知图(fuzzy cognitive maps, FCMs)。由于模糊逻辑能够比三值逻辑携带更多的信息,使得FCMs在定性推理中起着更大的作用,并成为目前认知图研究的主流,广泛应用于工业、军事、科技、医学、建筑等领域[3-7]。
FCMs用来解释系统中的概念、实体或者数学变量之间因果关系,利用有向加权图来建模,即由结点与结点之间的有向弧组成。结点间有向弧的权值反映了两个结点间的连接强度和类型。因此对FCMs的学习是尽可能找到准确的权值。FCMs的学习算法可大致分3类,分别是基于Hebbian的方法,基于进化算法的方法以及基于Hebbian和进化算法的混合方法。文献[8]提出的非线性Hebbian学习(nonlinear hebbian learning,NHL)算法是基于Hebbian方法中的代表算法,该算法需要专家的介入,而且对专家的知识精确性要求较高,但是在一些复杂领域的专家知识很难得到,容易出现初始网络无法重构的现象。为了解决这一问题,研究人员把进化算法应用于FCMs,使得FCMs可以自动选择数据。这种基于进化算法的选择策略,实质上是将选择问题转化为优化问题,通过设定合适目标函数的方法找到问题的最优解。文献[9]提出了用于学习FCMs的实数稀疏编码遗传算法(sparse real-coded genetic algorithms,SRCGA),该算法在实数编码遗传算法(real-coded genetic algorithms,RCGA)的基础之上采用密度估计参数,引导算法的学习过程。然而,预定义的密度参数在现实生活中很难求出,使得SRCGA在应用范围上存在一定局限性。由于系统的复杂性、概念间的相互作用及外部强迫函数的作用,概念间的关系可能会发生改变,甚至变为相互矛盾的关系,而FCMs不具有非单调推理的能力,这使得FCMs学习算法无法自适应于外界的环境变化。为了解决该问题,研究人员将多目标演化算法(multi-objective optimization evolutionary algorithms, MOEA)[10]用于FCMs的学习。该类算法针对不同的优先级,对多个目标函数进行折中处理以尽可能使所有目标同时达到最优,从而得到更为准确的FCMs。文献[11]设计了两个目标,使得输入的历史数据在不同数据密度情况下依然可以获得较优秀的解,从而为决策者提供不同属性的候选方案。多目标演化算法以非支配占优和精英保留机制为主要特点,可以对不同目标进行折中处理,单次运行后可以获得一组具有代表性的帕累托(Pareto)最优解集合,使各个目标尽可能同时达到最优。基于指标的多目标演化算法(indicator-based evolutionary algorithm,IBEA)[12]利用二元性指标直接计算适应度,提高了算法的收敛性,但是在维护解的多样性方面表现并不理想。文献[13]通过聚合函数权重矢量将子问题划分到指定邻域,通过子问题间的优化信息来优化个体本身,提出了基于分解的多目标演化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D),能够很好地解决一定规模范围内相异的多目标问题;基于外部存储引导的分解多目标演化算法(external archive guided MOEA/D,EAG-MOEA/D)[14]利用分解策略和非支配排序策略分别对内部种群和外部种群进行维护,使每一代的搜索区域更加明确,有效提高了多目标优化算法的搜索效率;基于排序和选择方法的MOEA/D(MOEA/D with sorting and selection,MOEA/D-SAS)[15]通过分解排序策略(decomposition based sorting,DBS)和角度选择策略(angle based selection,ABS),可以有效处理不规则的前沿,实现收敛性和多样性之间的平衡。
上述研究中,通过将多目标优化算法应用于模糊认知图,虽然能够有效地获得较为优秀的解,但依然存在一些不足:
(1) 以多个目标为优化对象对FCM进行学习的方法的出现,很好地降低了FCM对专家经验的依赖,但现有的算法在学习过程中仅对权值进行单方面优化,造成模型拟合准确程度不足;
(2) 将现有的多目标进化算法应用于FCM学习,虽然可以找到较为精确的权值,但是随着节点数目的增多,候选解的数目也会以指数级的速度增加,容易引起算法的收敛速度降低;同时,现有的多目标进化算法无法保证所得的解集分布较为均匀,导致算法容易陷入局部最优,使得现有的多目标进化算法无法适用于规模较大的FCM学习;
(3) 现有多目标FCM学习算法中的目标设计都偏重于对真实权重矩阵和学习权重矩阵之间的差异进行优化,忽略了响应序列对真实权重矩阵的影响,容易造成单个目标的解超出规定范围。
本文针对FCMs学习过程中仅对权值进行优化而造成模型拟合准确程度不足的缺陷,提出了一种基于多目标演化的模糊认知图学习算法(multiobjective evolutionary algorithm based on coordinate transformation for FCM, MOEA/CT-FCM)。该学习算法首先设计了基于坐标变换的MOEA(multi-objective optimization evolutionary algorithms based on coordinate transformation, MOEA/CT),该方法通过坐标变换(coordinate transformation, CT)策略赋予目标空间中个体新的适应度,并将此适应度值作为个体的收敛信息(convergence information, CI),完成个体CI的赋值,同时,采用一种新的外部存档策略,当精英个体进入存档集后,根据上一步得到的CI,对存档集中的个体进行筛选,从而寻找到有效收敛个体,加速收敛过程,进一步,引入一种基于Lp-norm的密度筛选方法,利用Fractional距离代替欧式距离,以准确反映个体间的拥挤程度,能够防止邻近个体同时被选入存档集,使所得解集分布更加均匀;接着,通过研究FCMs的固有特性,设计出结点间权值误差与误差权重2个求解目标,将FCMs的学习问题抽象为两目标优化问题,以防止单个目标的解集超出规定范围的问题;最后再将MOEA/CT算法应用于FCMs的模型学习。本文采用实际工程中9结点,12结点和24结点的FCMs进行仿真实验,实验结果表明本文提出的 MOEA/CT-FCM算法,相比于MOEA-FCM、RCGA、分治实数编码遗传(devide and conquer RCGA, D&C RCGA)、基于数据控制NHL算法(data and controlling NHL,DD-NHL)、NHL等算法,能够更准确地表达结点间的因果关系,降低对专家经验的依赖性。
1 模糊认知图
FCMs把知识蕴含在概念结点及概念结点间的关系中,通过概念间的依赖与反馈来模拟系统的动态行为,其数学模型包括概念结点C,权值w,状态值A,激活/阈值函数g(·)等组成部分[16]。
由Nn个概念结点所组成的结点矩阵可表示为
C=[C1,C2,…,CNn]
(1)
式中,Ci∈[0,1],i=1,2,…,Nn。这些结点之间的模糊因果关系可以用NN×NN维的邻接权重矩阵表示为
(2)

(3)

(4)
式中,β是用来规定函数在0点附近步长的参数,β的取值一般设置为5[19]。
2 MOEA/CT-FCM
2.1 MOEA/CT
针对基于传统占优机制的经典多目标智能算法在迭代过程中对精英种群判断力较弱,从而导致算法收敛缓慢和无法得到最优解的问题,本文在MOEA基础上提出了一种基于坐标变换的多目标演化算法,进行了3个部分改进:坐标变换策略、外部存储器更新策略和密度筛选策略。
2.1.1 坐标变换策略
为了寻找更为有效的收敛个体,以加速完成收敛过程,并快速逼近完整的Pareto真实前沿,MOEA/CT算法设计了坐标变换策略。首先以目标空间中的每个个体i为原点依次建立坐标系,将其余个体以目标值为基准投影至新坐标系中,产生新的个体,并将个体i与新个体的欧氏距离和作为个体i的新适应度Dpi表示为
(5)

以两目标优化算法为例,来说明坐标变换模型的建立及个体适应度调整方式,如图1所示,点A(3,3),B(1,6),C(6,2),D(8,1)为目标空间中的4个非支配解,现以点A为中心建立坐标系,计算各个体在新坐标系下距点A的欧式距离。点B(1,6)在目标f1上优于点A,则将点B沿f2方向平移到新坐标系中,得到调整后的点B′(-2,0),同理可得C′(0,-1),D′(0,-2),可得个体A的新适应度为DA=5。

图1 CT策略示意图Fig.1 Schematic diagram of CT strategy
2.1.2 改进的外部存储器更新策略

(6)
式中,g表示当前迭代次数;gmax表示迭代总次数;dj(min)、dj(max)分别表示经调整后其余个体距个体j的最小值与最大值;α值表示目标函数个数。
最终通过对非支配解集进行进一步筛选,寻找到更为有效的收敛个体,加速收敛过程。
α的选取会对算法的收敛性造成一定的影响,本文以ZDT1(E.Zitzler,K.Deb and L.Thiele)函数为例,比较不同取值的α对算法性能的影响。如图2所示,随着迭代次数的增加,收敛性指标γ都呈下降趋势,当α=2时,γ下降速率较α取其他值时更具优势,说明α取值为2时,算法的收敛速率最快。图2中各曲线在开始时都有一定的波动,这是由于MOEA/CT算法在初始化阶段采用随机选取个体的方式,导致算法的收敛过程需要经过多次的迭代才能趋于稳定,而从图2中可以看出,当α取值为2时,波动的次数较少,说明其到达稳定状态所需的迭代次数较少。因此本文α取值为2。
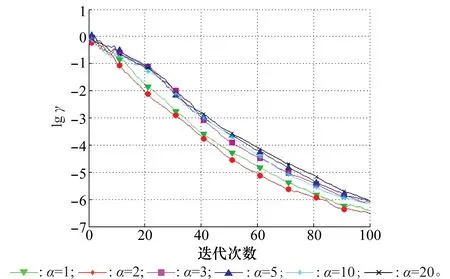
图2 不同α值对算法性能的影响Fig.2 Effects of different α values on the performance of the algorithm
2.1.3 改进的密度选择策略
在现有多目标优化算法中,经常使用的拥挤密度估计方法如:Mahalanobis、Euclidean(L2-norm)平均距离算法等[20-22],在目标函数个数增多的情况下并不能准确反映个体间的拥挤程度[23]。文献[23-24]指出,相比L2-norm距离,Fractional距离(Lp-norm)在处理高维空间问题时效率更高。文献[25]在上述结论基础上,通过实验证明,通过减小p值可以使最远相邻个体和最近相邻个体的计算结果形成较大反差,因此MOEA/CT采用p=1/m时的Fractional距离代替欧式距离计算拥挤距离,以使非支配个体分布更均匀。
为了验证MOEA/CT算法所设计的3个策略的有效性,本文采用世代距离指标(generational distance,GD)[26],均匀性指标(spacing,SP)[27],收敛性指标γ[28],在ZDT1和ZDT2函数上进行实验。分别选取MOEA算法基础上引入坐标变换策略(transformation function,TF)、坐标变换策略结合改进的外部存储器策略(TF evolutionary algorithm,TFEA)以及坐标变换策略与改进外部存储器策略结合密度选择3种情况,下文简称MOEA/TF、MOEA/TFEA及MOEA/CT算法,与MOEA算法进行对比。实验结果如表1所示,表1中数据为各算法迭代100次,独立运行30次所取的平均值。从表1可以看出,采用了本文提出策略的3种算法,实验结果较MOEA更优。MOEA/TF算法仅选取经过坐标变换后适应度较大的个体加入外部存储器,直至外部存储器满为止。表1中,MOEA/TF算法的GD和γ比MOEA算法更小,说明采用坐标转换策略后,算法所选取的个体与真实前沿较为接近,但是随着迭代次数的增多,非支配解数量成倍增加,仅依靠坐标变换策略无法对大量非支配解进行有效筛选,因此本文设计了更为有效的外部存储器筛选策略。MOEA/TFEA算法所得结果的GD和γ值较MOEA/TF算法更小,说明加入本文提出的外部存储器策略之后,能够使得算法所选择的个体更加贴近真实前沿。由于算法未对所获的解集进行合适的密度筛选,导致MOEA/TF与MOEA/TFEA算法的SP值并不理想,因此本文加入了Lp-norm密度筛选策略,以使得所选解集的密度更加均匀。同样从表1中可以看出,MOEA/CT算法的SP值较小,说明密度筛选策略能够使得所选解集的密度更加均匀。

表1 不同策略对算法的影响
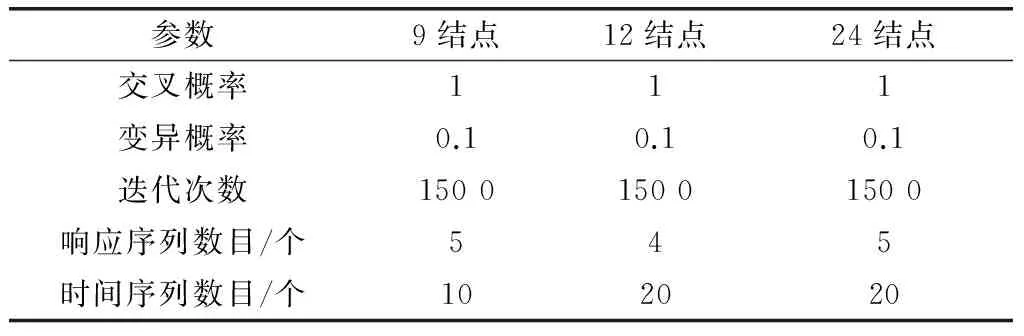
为了充分检验MOEA/CT算法的性能,本文还将所提算法与改进的非支配排序遗传算法(improved non-dominated sorting genetic algorithm,NSGA-Ⅱ)[29], 多目标粒子群算法(multi-objective particle swarm optimization,MOPSO)[30], NSGA-Ⅲ[31], 改进的两阶段存储法(improved two-archive algorithm,Two_arch2)[25]这4种算法进行对比。本文采用与文献[9]一样的模拟二进制交叉(simulated binary crossover,SBX)交叉算子和多项式变异算子,所有对比算法的控制参数设置均采用相应原文文献中的推荐值,实验参数如表2所示。
实验结果均为各算法独立运行30次所对应的各测试指标平均值,统计结果如表3所示,各项对比实验中的最优结果均用黑体加粗表示。

表2 实验参数设置
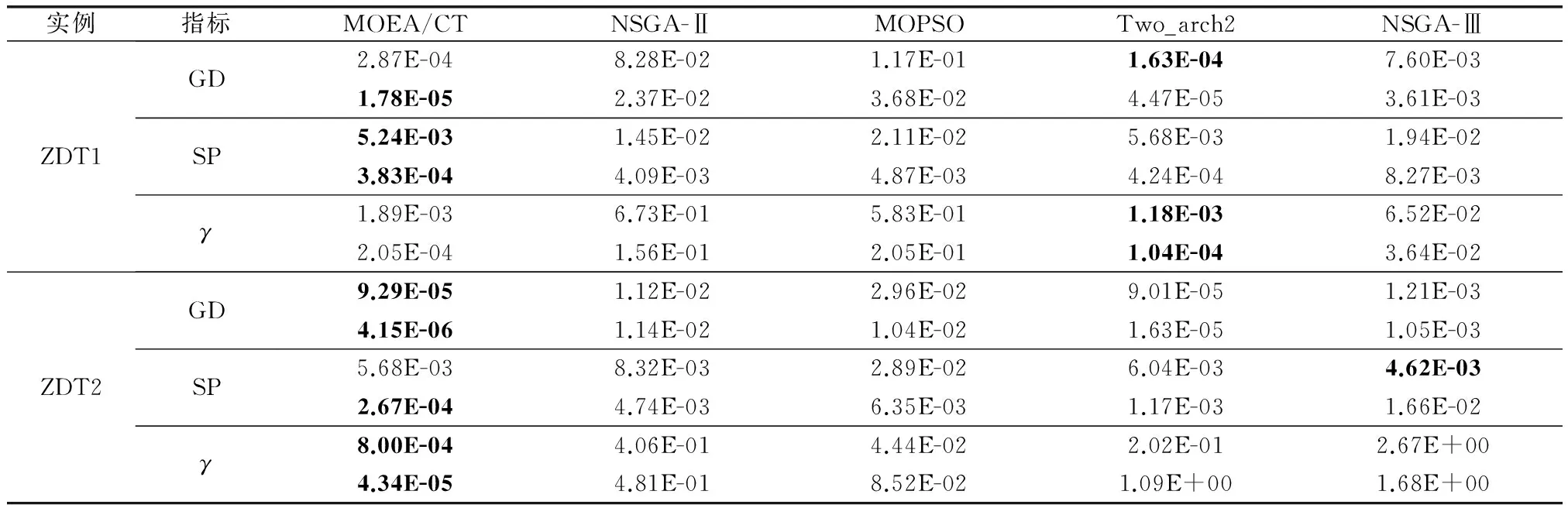
表3 5种算法在ZDT1与ZDT2上的实验结果
ZDT1函数非劣解集在目标函数空间是凸的,从表3可以看出,MOEA/CT、Two_arch2,NSGA-Ⅲ都可以很好逼近真实Pareto前沿,但是MOEA/CT算法具有更好的分布性。NSGA-Ⅲ没有覆盖整个Pareto前沿面,NSGA-Ⅱ和MOPSO算法虽然有收敛趋势,但并没有完全收敛。MOEA/CT在ZDT1函数所得到的前沿如图3所示。

图3 MOEA/CT的ZDT1函数前沿Fig.3 MOEA/CT front of ZDT1 function
ZDT2函数的非劣解集在目标函数空间是非凸的,本算法在各测试指标上表现都很优秀,分布均匀,贴近真实前沿且解集的分布宽广度与真实前沿一致。NSGA-Ⅲ在求解ZDT2时,分布性略优于MOEA/CT算法。但是较大的GD值说明其未能逼近整个真实前沿面。MOPSO算法的GD与γ值较小,但是SP值较大,说明其陷入局部最优无法跳出。MOEA/CT在ZDT2函数所得到的前沿如图4所示。

图4 MOEA/CT的ZDT2函数前沿Fig.4 MOEA/CT front of ZDT2 function
2.2 面向FCMs学习的两目标优化模型设计
在多目标优化中,通过Pareto最优解来评价所得解集的优劣性,优劣性就是指在目标函数的解集中对其中一个或多个子目标函数的进一步优化,而不会引起其他子目标函数的解超出规定范围,即多目标优化最终会得到一组互相支配的解的集合。
对FCMs学习的目的是通过优化权值矩阵,尽可能确定每一对概念结点之间的真实关系。因此,算法将所求得的响应序列和现有的响应序列之间的最小差异设定为第一目标,表示为
(7)
第2个目标是误差比重,用来评估真实权重矩阵和学习权重矩阵的差异,并与全局数据误差进行比较。结点i的误差比重计算方式为
(8)
由FCM性质可知,希望通过算法得到尽可能小的结点差异和权重差异,因此误差比重越小,代表算法所得到的解集越接近真实解集。多目标优化是对多个相互矛盾、相互影响的目标进行优化,以求得最优解,能够同时满足多个矛盾的目标函数。由式(7)、式(8)可推知,当式(7)的值增加时,式(8)的值会在一定程度上减小,而当式(8)的值增加时,式(7)的值不一定增加。实际运行所得结果如图5所示,其中权重值和结点值的取值范围为[0,1],可以看出两个目标函数之间相互排斥。因此,本文所设计的两个最小化目标是相互矛盾且相互影响的,符合多目标定义且适用于FCMs系统。
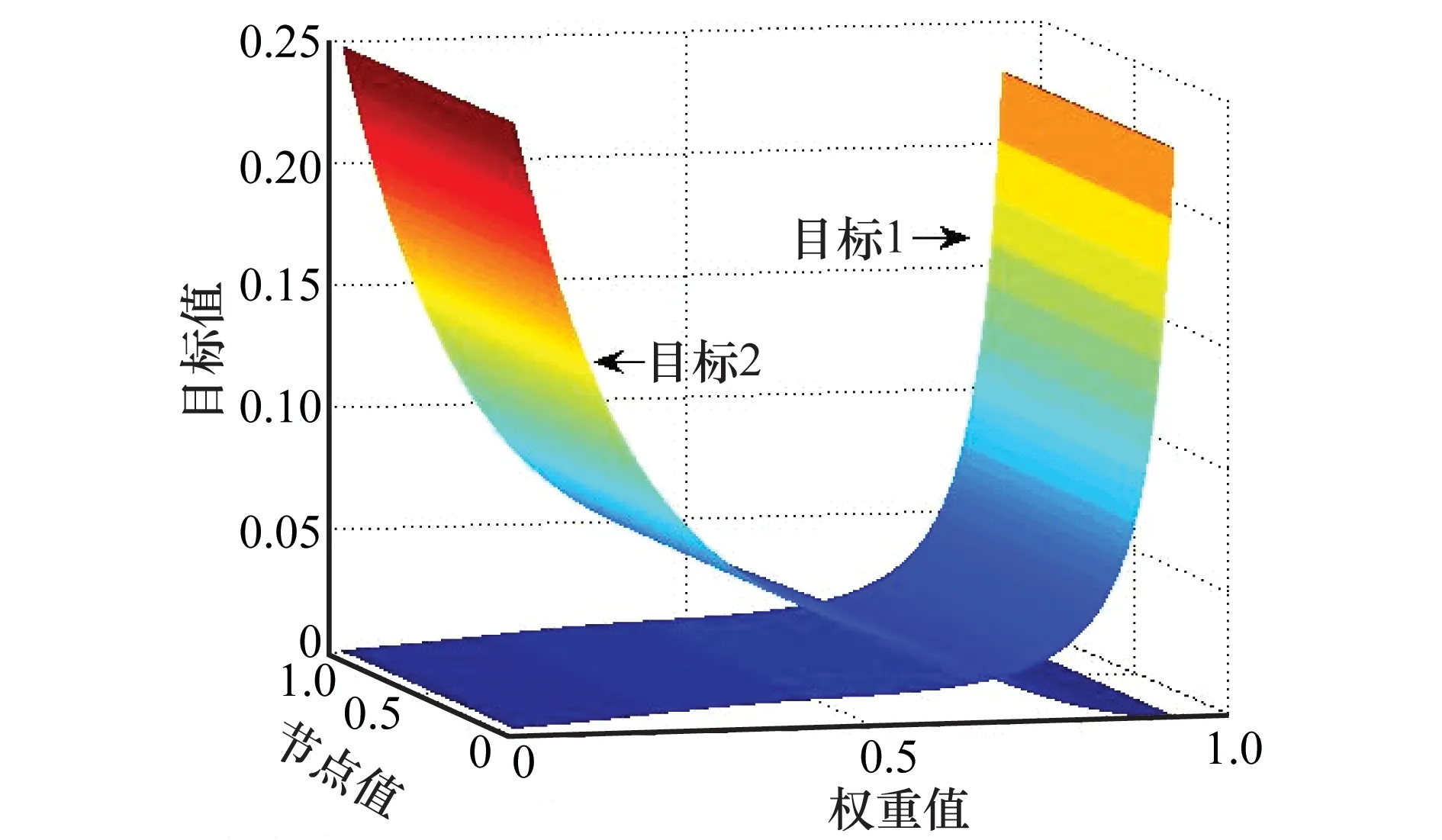
图5 两个目标的关系Fig.5 Relationship between the two objectives
2.3 MOEA/CT-FCM
在MOEA/CT中,每一个候选解由一维向量组成,而在 MOEA/CT-FCM中每个候选解由一个权重矩阵组成。为了方便起见,把2维权重矩阵转化为1维的向量,若权重矩阵如式(2)所示,则转化后的Nn×Nn的权重可表示为
w=[w11,w12,…,w1Nn,w21,w22,…,
w2Nn,…,wNn1,…,wNnNn]
(9)
式中,w的取值范围为[-1,1]。
MOEA/CT-FCM算法的具体实现过程如下:
步骤1生成初始种群,即初始权重矩阵;
步骤2进行非支配排序后执行进化操作生成子代种群,合并种群后进行非支配排序选择;
步骤3判断剩余的种群数量是否大于预设值,若小于预设值则继续执行步骤2直至数量大于预设值;
步骤4若数量大于预设值进行坐标变换找到收敛性较好的个体,通过函数筛选更新外部存储器,之后进行密度筛选,得到不大于种群数量的精英种群;
步骤5判断是否达到总迭代次数,若未达到则返回步骤2,反之,运行结束。
MOEA/CT-FCM的具体过程如下:
算法1基于多目标演化的模糊认知图学习算法
输入初始种群Pt,迭代次数gmax,种群数目N,标识目标函数个数m
输出新种群Pt+1

2 初始化迭代次数:g=1;
3 对初始种群Pt进行非支配选择,选择出其中互相不支配的个体,将结果存入种群Qt;
4 While |Qt|≤N{


7 }

9 Fori=1:|Qt| {
10 Forj=1:|Qt| {
11 Fork=1:m{
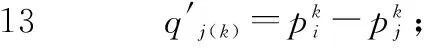
14 }
15 }

17 }

19 Fori=1:|Qt′| {
20 对个体进行归一化操作,得到归一化后的新个体适应度γi;
21 利用式(6)计算Oi;
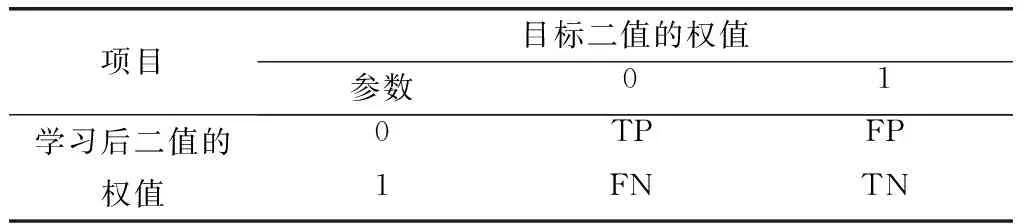
22 将γi 23 } 24 利用密度选择策略,对Qt中的个体进行筛选,将结果存入新种群Pt+1 本文主要的运算量是计算经过坐标变换策略调整及收敛距离、Pareto占优过程和拥挤距离的计算。若有m个目标,种群数量为N,计算坐标变换和收敛距离的复杂度为O((mN)2),非支配排序所需计算复杂度为O(NlogM-2N)[32],求解拥挤距离所需计算复杂度最大为O((mN)2)。综上所述,本算法的时间复杂度为max(O(NlogM-2N),O((mN)2))。 本文对3种不同规模的实际FCM进行学习,分别来源于9结点的工厂监控系统[33],12结点的巴西亚马逊森林砍伐模型[34]和24结点的某学校教育软件模型[35]。9结点模型与12结点模型的概念结点为确定性结点,24结点模型为随机不确定性结点。 MOEA/CT-FCM应用于9结点模型初始参数设置与文献[33]相同,12结点模型初始参数设置与文献[34]相同,24结点模型初始参数为范围在[0,1]之间的随机设定值,具体参数设置如表4所示,其中,Nn表示结点个数;Ns表示响应序列个数;Ns表示时间序列数目(设定方式详见第3.2节)。 表4 MOEA/CT-FCM实验参数设置 分别选取Data_error, Model_Error, Out_of_Sample_Error和SS_Mean作为算法的评价指标。其中,Data_error是目标函数f1(W)。模型误差Model_Error用以评价算法获得的权值与初始权值之间的差异,表示为 (10) Out_of_Sample_Error用于评价算法的拟合能力,表示为 (11) SS_Mean利用统计特性Specificity和Sensitivity来验证学习算法是否能够准确预测出2个结点之间存在的边,并把模糊认知图学习问题扩展和转换成了二分类问题。当权重的绝对值大于临界值时被置为1,而小于临界值时则置为0。为了进行比较,本文将采用与文献相同的临界值以及正负结果的定义,此处设临界值为0.05。另外,本算法中将权重的绝对值小于0.05的边识别为正边,否则该边被识别为负边。转换过程中,T代表正确识别,F代表错误识别,P代表正边,N代表负边。式(12)、式(13)中N表示满足条件的边的数目。SS_Mean值越接近1,表示算法预测权值的准确性越强,其参数设置如表5所示。 表5 SS_Mean参数设置 Specificity、Sensitivity、SS_Mean表示为 (12) (13) (14) 为了能够降低MOEA/CT-FCM的计算代价,使FCM尽快达到较稳定的学习状态,本文针对模糊认知图时间序列数目的确定进行实验。为保证实验的客观性,本文分别对9结点,12结点和24结点的结点值进行随机初始化,图6展示了9结点网络模型时间序列长度为10的响应序列变化曲线,图7展示了12结点网络模型时间序列长度为20的响应序列变化曲线。 图6 9结点时间序列长度与结点状态Fig.6 Time sequence and data statements of 9 nodes 图7 12结点时间序列长度与结点状态Fig.7 Time sequence and data statements of 12 nodes 以Nt(9)表示9个结点的时间序列数目,Nt(12)表示12个结点的时间序列数目,从图6可以看出,在Nt(9)=5之前,各结点的变化值均不稳定,这是因为各个算法中下一个时间结点数值需要由当前时间结点值和权值的共同作用决定,由于初始权值是随机产生的,因此在学习过程中结点会产生波动。从Nt(9)=5时刻开始,结点状态变化幅度逐渐减小,说明模糊认知图的动力学系统开始变得稳定。在确定Nt(12)时,采用了文献[34]的第一序列,由图7可以看出,最终各结点值都稳定在[0,1],这是由FCM框架的性质决定,由于初始结点C6=1.4,C7=-0.4,C8=-0.2,导致Nt(12)=4之前结点波动极大,在Nt(12)=12 之后各结点状态趋于稳定,本文最终选取Nt(12)=20。24结点的时间序列数目的确定与12结点相同,在此不多做赘述。因此,在MOEA/CT-FCM中,我们选择Nt(9)=10,Nt(12)=20,Nt(24)=20。 为了比较MOEA/CT-FCM的优化性能,将本文所提算法与MOEA-FCM[11]、RCGA、D&C RCGA[36]、DD-NHL[37]、NHL[8]等5种算法做对比。表6为9结点实验结果对比,实验结果均为各算法独立运行30次所对应的各测试指标的平均值和标准差,各项对比试验中的最优结果均用黑体加粗表示。对比算法的实验结果来源于文献[11],“/”表示在原文献中未给出测量值。MOEA/CT-FCM算法在4个评价指标上均明显优于其余5种算法。9结点工厂监控模型中,MOEA/CT-FCM,MOEA-FCM,RCGA,D&C RCGA在Data_Error上都取得了0.00的结果,在结点还原方面比DD NHL和NHL要优秀,其中MOEA/CT-FCM,MOEA-FCM在Out_of_Sample_Error上优于其他算法,说明在相同结点的情况下其拟合能力更强。由SS_Mean值可以看出,MOEA/CT-FCM能正确学习权值的大小。 表6 9结点实验结果对比 表7为12结点实验结果对比。结合表7中SS_Mean值和Model_Error值可以看出,MOEA/CT-FCM不仅可以正确识别概念结点状态的变化,在计算概念结点间权值方面的误差也很小。结合表7种Data_Error值和Model_Error值可以看出,MOEA/CT-FCM的值明显小于其余5种算法,说明在算法中所设计的f2(w)目标在一定程度上起到了平衡概念结点状态值和权值的作用。表8为24结点实验结果对比。表8反映了 MOEA/CT-FCM在处理不确定性多结点问题的能力。虽然RCGA,D&C RCGA,DD NHL,NHL算法并没有对Model_Error,SS_Mean进行实验,但并不影响对算法响应序列稳定程度的观测。MOEA/CT-FCM,MOEA-FCM的Data_Error值明显较其余对比算法小,说明MOEA/CT-FCM与MODE-FCM能够准确地还原概念间权值。但MOEA-FCM的SS_Mean值较小,说明在结点数量增多的情况下,该算法并不能很好的识别结点之间的关系。因此,虽然MOEA-FCM表现很出色,但是相比MOEA/CT-FCM来说略显逊色。 表7 12结点实验结果对比 表8 24结点实验结果对比 模糊认知图具有强大的推理能力,利用其来处理工程建模问题具有较强的可行性,同时对数据的预测具有重要的实际意义。本文通过设计结点间有向弧权值误差与误差比重两个目标,提出了模糊认知图学习的多目标优化模型,利用基于坐标变换的多目标演化算法对该模型进行优化求解,有效提高了模糊认知图的学习精度。通过实验结果可以看出,基于多目标演化的模糊认知图学习算法可以有效降低结点数据误差与模型误差,能够更准确地得出概念结点间的因果关系,同时能够适用于不同的实验数据集,说明本文所提出的算法具有一定的应用前景。 [1] 骆祥峰. 认知图理论及其在图像分析与理解中的应用[D]. 合肥: 合肥工业大学, 2003. LUO X F. Cognitive map theory and its applications in image analysis and understanding[D].Hefei:Hefei University of Technology, 2003. [2] KOSKO B. Fuzzy cognitive maps[J]. International Journal of Man-Machine Studies, 1986, 24(1): 65-75. [3] 陈军, 高晓光, 丁琳. 模糊认知图在预警机燃油管理中的应用[J]. 系统工程与电子技术, 2008, 30(9): 1717-1720. CHEN J, GAO X G,DING L. Application of fuzzy cognitive maps in fuel management of airborne warning and control systems[J]. Systems Engineering and Electronics, 2008, 30(9): 1717-1720. [4] 李闯,端木京顺,雷英杰,等.基于认知图和直觉模糊推理的态势评估方法[J].系统工程与电子技术,2012,34(10):2064-2068. LI C, DUANMU J S, LEI Y J, et al. Situation assessment based on cognitive maps and intuitionistic fuzzy reasoning[J]. Systems Engineering and Electronics, 2012, 34(10): 2064-2068. [5] MENDONCA M, ARRUDA L V R, ROSSATO CHRUN I, et al. Hybrid dynamic fuzzy cognitive maps evolution for autonomous navigation system[C]∥Proc.of the IEEE International Conference on Fuzzy Systems, 2015: 1-7. [6] PAPAGEORGIOU E I. A new methodology for decisions in medical informatics using fuzzy cognitive maps based on fuzzy rule-extraction techniques[J]. Applied Soft Computing, 2011, 11(1): 500-513. [7] SENNIAPPAN V, SUBRAMANIAN J, PAPAGEORGIOU E I, et al. Application of fuzzy cognitive maps for crack categorization in columns of reinforced concrete structures[J]. Neural Computing & Applications, 2016: 1-11. [8] PAPAGEORGIOU E, STYLIOS C, GROUMPOS P. Fuzzy cognitive map learning based on nonlinear hebbian rule[C]∥Proc.of the Australian Conference on Artificial Intelligence, 2003:256-268. [9] STACH W, PEDRYCZ W, KURGAN L A. Learning of fuzzy cognitive maps using density estimate[J]. IEEE Trans.on Systems Man & Cybernetics Part B Cybernetics, 2012, 42(3):900. [10] DEB K. Multi-objective ptimization using evolutionary algrithms[M]. Chichester: Wiley, 2001. [11] CHI Y, LIU J. Learning of fuzzy cognitive maps with varying densities using a multiobjective evolutionary algorithm[J]. IEEE Trans.on Fuzzy Systems, 2016, 24(1): 71-81. [12] ZITZLER E, KÜNZLI S. Indicator-based selection in multi-objective search[J].Lecture Notes in Computer Science,2004,3242: 832-842. [13] ZHANG Q, Li H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Trans.on Evolutionary Computation, 2007,11(6): 712-731. [14] CAI X, LI Y, FAN Z, et al. An external archive guided multi-objective evolutionary algorithm based on decomposition for combinatorial optimization[J]. IEEE Trans.on Evolutionary Computation, 2014, 19(4): 508-523. [15] CAI X, YANG Z, FAN Z, et al. Decomposition-based-sorting and angle-based-selection for evolutionary multiobjective and many-objective optimization[J]. IEEE Trans.on Cybernetics, 2016, 47(9): 1-14. [16] KOSKO B. Fuzzy cognitive maps[J]. International Journal of Man-machine Studies, 1986, 24(1): 65-75. [17] TSADIRAS A K. Comparing the inference capabilities of binary, trivalent and sigmoid fuzzy cognitive maps[J]. Information Sciences, 2008, 178(20): 3880-3894. [18] CHEN N, ZHANG J. Index-based genetic algorithm for continuous optimization problems[C]∥Proc.of the Genetic and Evolutionary Computation Conference, 2011: 1029-1036. [19] STACH W J. Learning and aggregation of fuzzy cognitive maps-an evolutionary approach[D]. Canada: University of Alberta. 2010. [20] PSYCHAS I D, DELIMPASI E, MARINAKIS Y. Hybrid evolutionary algorithms for the multiobjective traveling salesman problem[J]. Expert Systems with Applications, 2015, 42(22): 8956-8970. [21] HUANG D Z, GONG R X, SHU N M. Constrained multi-objective optimization for microgrid based on nondominated immune algorithm[J]. IEEE Trans.on Electrical & Electronic Engineering, 2015, 10(4): 376-382. [22] LI M, YANG S, ZHENG J, et al. ETEA: a euclidean minimum spanning tree-based evolutionary algorithm for multi-objective optimization[J].Evolutionary Computation, 2014, 22(2): 189-230. [23] AGGARWAL C C, HINNEBURG A, KEIM D A. On the surprising behavior of distance metrics in high dimensional space[C]∥Proc.of the 8th International Conference on Database Theory, 2001: 420-434. [24] MORGAN R, GALLAGHER M. Sampling techniques and distance metrics in high dimensional continuous landscape analysis: limitations and improvements[J]. IEEE Trans.on Evolutionary Computation, 2014, 18(3): 456-461. [25] WANG H D, JIAO L C, YAO X. Two_arch2: an improved two-archive algorithm for many-objective optimization[J]. IEEE Trans.on Evolutionary Computation, 2015, 19(4): 524-541. [26] VELDHUIZEN D V, LAMONT G B. On measuring multi-objective evolutionary algorithm performance[C]∥Proc.of the Evolutionary Computation, 2000: 204-211. [27] SCHOTT J R. Fault tolerant design using single and multicriteria genetic algorithm optimization[J].Cellular Immunology,1995, 37(1): 1-13. [28] DEB K, THIELE L, LAUMANNS M, et al. Scalable multi-objective optimization test problems[C]∥Proc.of the World on Congress on Computational Intelligence, 2002: 825-830. [29] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans.on Evolutionary Computation, 2002, 6(2): 182-197. [30] COELLO C C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Trans.on Evolutionary Computation, 2004, 8(3): 256-279. [31] DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE Trans.on Evolutionary Computation, 2014, 18(4): 577-601. [32] KUNG H T, LUCCIO F, PREPARATA F P. On finding the maxima of a set of vectors[J]. Journal of the ACM, 1975, 22(4): 469-476. [33] STYLIOS C D, GROUMPOS P P. Fuzzy cognitive maps: a model for intelligent supervisory control systems[J]. Compu-ters in Industry, 1999, 39(3): 229-238. [34] KOK K. The potential of fuzzy cognitive maps for semi-quantitative scenario development, with an example from Brazil[J]. Global Environmental Change, 2009, 19(1): 122-133. [35] HOSSAIN S, BROOKS L. Fuzzy cognitive map modelling educational software adoption[J]. Computers & Education, 2008, 51(4): 1569-1588. [36] STACH W, KURGAN L, PEDRYCZ W, et al. Genetic learning of fuzzy cognitive maps[J].Fuzzy Sets & Systems,2005,153(3): 371-401. [37] STACH W, KURGAN L, PEDRYCZ W. Data-driven nonlinear Hebbian learning method for fuzzy cognitive maps[C]∥Proc.of the IEEE International Conference on Fuzzy Systems, 2008: 1975-1981.3 实验结果
3.1 实验参数
3.2 时间序列数目确定


3.3 实验结果

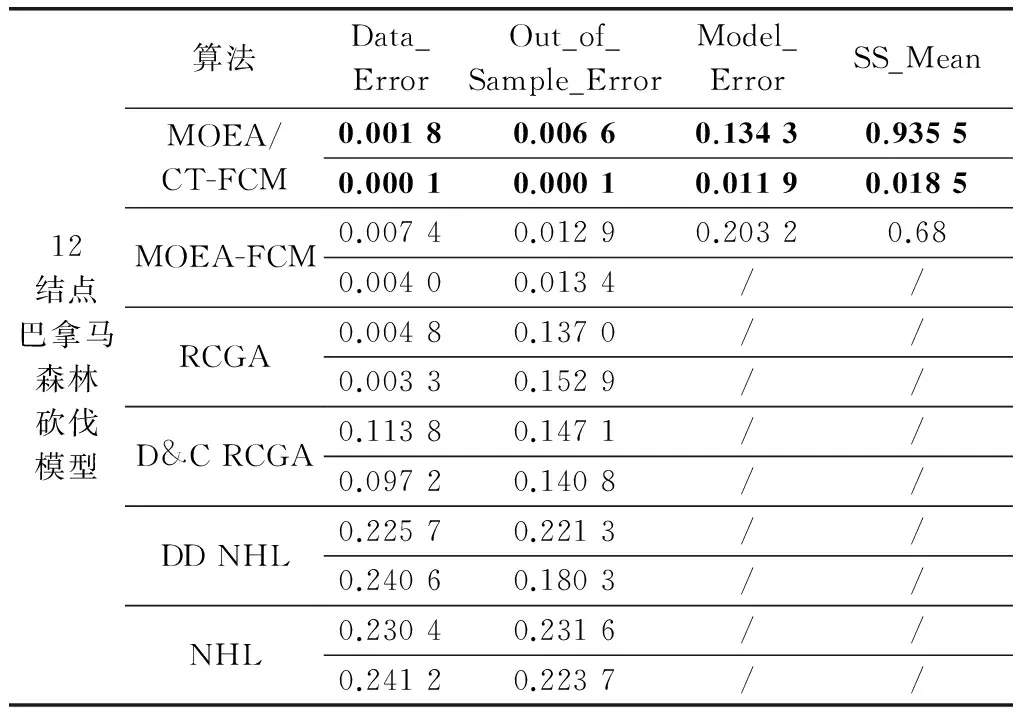
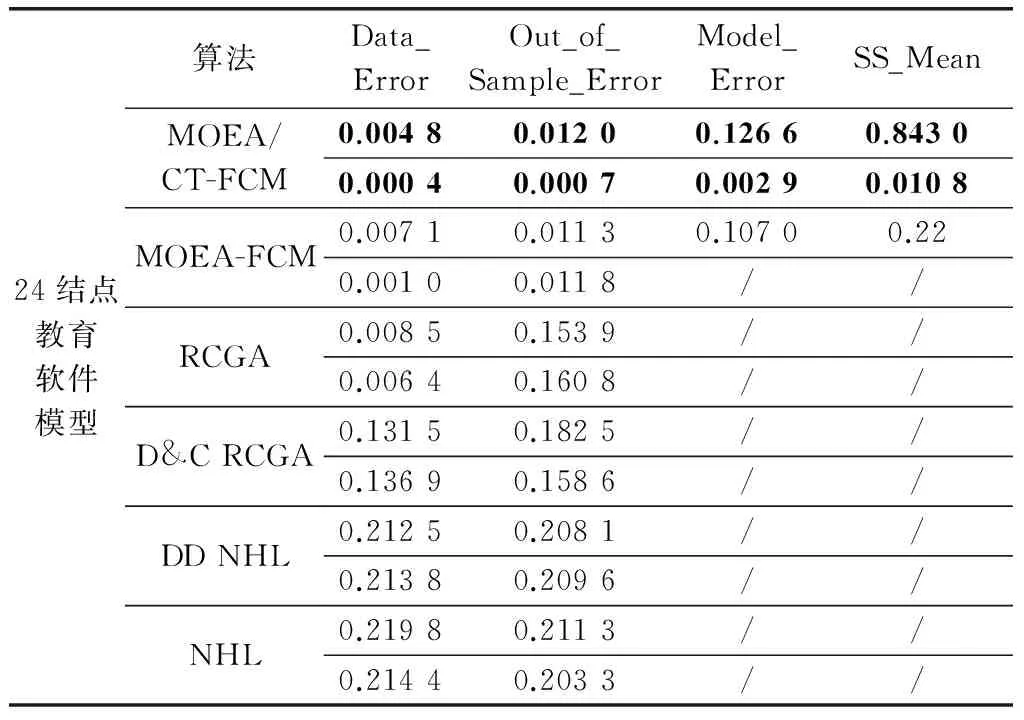
4 结 论

