基于四通道不可分提升小波的多聚焦图像融合

刘 斌, 付忠旺

(湖北大学计算机与信息工程学院, 湖北 武汉 430062)

0 引 言

近年来,传感器的技术发展迅速,其发展过程中延伸出一系列新的问题,如单一传感器的信息量不能满足实际应用的需要。针对此问题,使用数据融合技术对多源数据进行处理成为一种重要的解决方案。图像融合是二维数据融合的核心。文献[1]定义图像融合为将两幅或者多幅图像使用一定的方法合成为一幅新图像,新图像具有更好的性能和特点。多聚焦图像融合是图像融合的重要分支,它将同一场景多个不同聚焦点的图像合成为一个处处都清晰的图像,可以很好地解决光学成像系统聚焦范围有限导致的图像局部不清晰的问题。

近十多年来,图像融合方法如雨后春笋般涌现,基于多分辨分析的融合方法以其具有良好的特性而成为这些方法的主流,它主要包含经典的基于金字塔变换的融合方法和现代的基于小波变换的融合方法[2-5],而经典的基于金字塔变换的融合方法因其具有较多的数据冗余性和不具有方向性而逐渐被改进和发展。随着小波理论的不断发展,基于小波变换的融合方法层出不穷,展现了新的生命力。基于小波变换的融合方法包括传统的基于张量积小波分解的图像融合方法和基于不可分小波分解的图像融合方法。比较而言,基于不可分小波的图像融合方法在传统基于张量积小波的融合方法只强调水平和垂直方向的基础上实现了各向同性的效果。但是,不可分小波分解采用了大量的滤波器卷积运算,算法的空间复杂度很高,而且算法的融合速度很慢。

一维提升小波利用Laurent多项式的带余除法,把一维小波变换和多尺度分析的多相位矩阵分解为一系列2×2的右上三角矩阵和左下三角矩阵的乘积,从而把一维小波多尺度分析的卷积和下抽样过程变为连续乘积来实现,被称为第2代小波[6],相对于第1代小波变换理论,第2代小波有以下优点:小波的构造完全在时域内进行,无须傅里叶理论;建立了与Mallat算法功能相同的提升格式算法;运算过程简单,具有快速算法,计算更迅速;可实现即位运算, 节省内存;可实现整数到整数的变换,从而实现了基于小波的无损处理技术。这些特点在图像处理与识别中得到了广泛的应用。

目前，二维提升小波的构造依靠一维提升小波来实现,通过一维提升小波的张量积得到的二维提升小波。这是二维小波变换的一种特殊的提升方式,不是一般的提升方案。那么,二维小波变换的提升能否像上述一维小波变换那样,利用Euclidean除法把二维小波变换的多相位矩阵分解为上、下三角矩阵的乘积呢？答案是否定的。因为二元Laurent多项式不存在带余除法,因而不能通过Euclidean除法解决二维小波变换提升的一般方案。通过查阅文献所知,目前还没有关于二维四通道不可分小波的提升方案的研究。本文试图利用矩阵分解方法,找到二维四通道不可分小波的滤波器组,把其多相位矩阵进行提升分解,并利用此原理对图像融合中的源图像进行分解和重构。

1 二维四通道不可分小波滤波器组的构造

文献[7]提出了高维不可分小波的构造方法,其构造的低通滤波器形式为

(1)

其相应的s-1(s=det(A))个CQF滤波器的形式为

ξ∈Rd;j=1,2,…,s-1

(2)

设小波变换时的伸缩矩阵为A=[2,0;0,2],则具有紧支撑、正交性的2P×2P的滤波器组可表示为

{M0(x,y),M1(x,y),M2(x,y),M3(x,y)}=

(3)

式中,x=e-i ω1,y=e-i ω2;Uj(j=1,2,…,K)为正交阵,V/2=(V0,V1,V2,V3)/2为正交阵;D(x,y)=diag(1,x,y,xy);V1,V2,V3为4×1向量,V0=(1,1,1,1)T。

为构造4×4的具有对称性的滤波器组,取K=1,构造

且取

构造

可以验证U1为中心对称的正交矩阵,V/2为正交矩阵。这样构造出的滤波器组具有正交性、对称性、紧支撑性。根据上述构造方法可以设计出多组二维不可分小波滤波器组,通过实验,选择如下参数α1=-π/9,α2=-π/7,β1=-π/7,β2=π/8时的一组滤波器组的时域形式为

(4)

2 二维四通道不可分小波滤波器组的提升方案

2.1 二维四通道不可分小波多相位矩阵的提升方案

文献[6]利用一元多项式的带余除法,成功地将一维小波多相位矩阵分解为单位左下三角矩阵、单位右上三角矩阵以及对角线矩阵的连乘积,从而把一维小波变换进行了提升,由于二元多项式不存在带余除法,使得二维不可分小波不能像一维小波那样利用带余除法对其多相位矩阵进行分解,在第1节设计的二维四通道不可分滤波器组的基础上,对其多相位矩阵进行了成功的提升分解。具体分解过程如下。

和一维多相位矩阵定义类似,也可以定义二维提升小波的多相位矩阵为

P(x,y)=

(5)

式中

(6)

根据上述定义,可以得到式(4)所表示的滤波器组的多相位矩阵为

P(x2,y2)=

(7)

分别把式(7)中的x2换成x,y2换成y,得多相位矩阵为

(8)

转化为左上三角和右下三角表示为

(9)

令参数为

2.2 基于多相位矩阵提升方案的图像分解与重构

基于傅里叶变换理论和卷积理论的第一代小波对于图像的分解所使用的方法是分别利用所设计的小波低通滤波器和小波高通滤波器分别对图像进行卷积,然后进行下2抽样;而重构图像时则是先进行上2插值,然后分别使用重构小波低通滤波器和小波高通滤波器进行卷积。而有了多相位矩阵这个系统算子后,就可以把多相位矩阵直接作用于抽样后的图像子集上,得到分解子图像,重构时则使用其逆矩阵作用于子图像上,得到重构结果图像。而从以上多相位矩阵的提升方案可以看出,多相位矩阵的作用可以分步进行,即分别使用左下三角矩阵和右上三角矩阵连续作用于抽样后的子集上,完成图像的提升分解,从而得到图像的低频成份和高频成份。另外,分析运算的复杂性(第4节)可知,这样的上、下三角矩阵作用于图像上可以大大节约运算量,加速图像分解和重构速度。利用上述多相位矩阵对图像分解和重构的具体过程如下:

(1) 将原始图像x0分解成4个子集x、y(1)、y(2)、y(3),确保其互不相交，即

(10)

(2) 进行提升分解，即

(11)

分别使用Predict1和Predict2进行预测,使用Update1和Update2进行更新。图1为提升小波变换分解过程中的一次预测更新过程,其中Predict代表Predict1或Predict2,Update代表Update1或Update2。

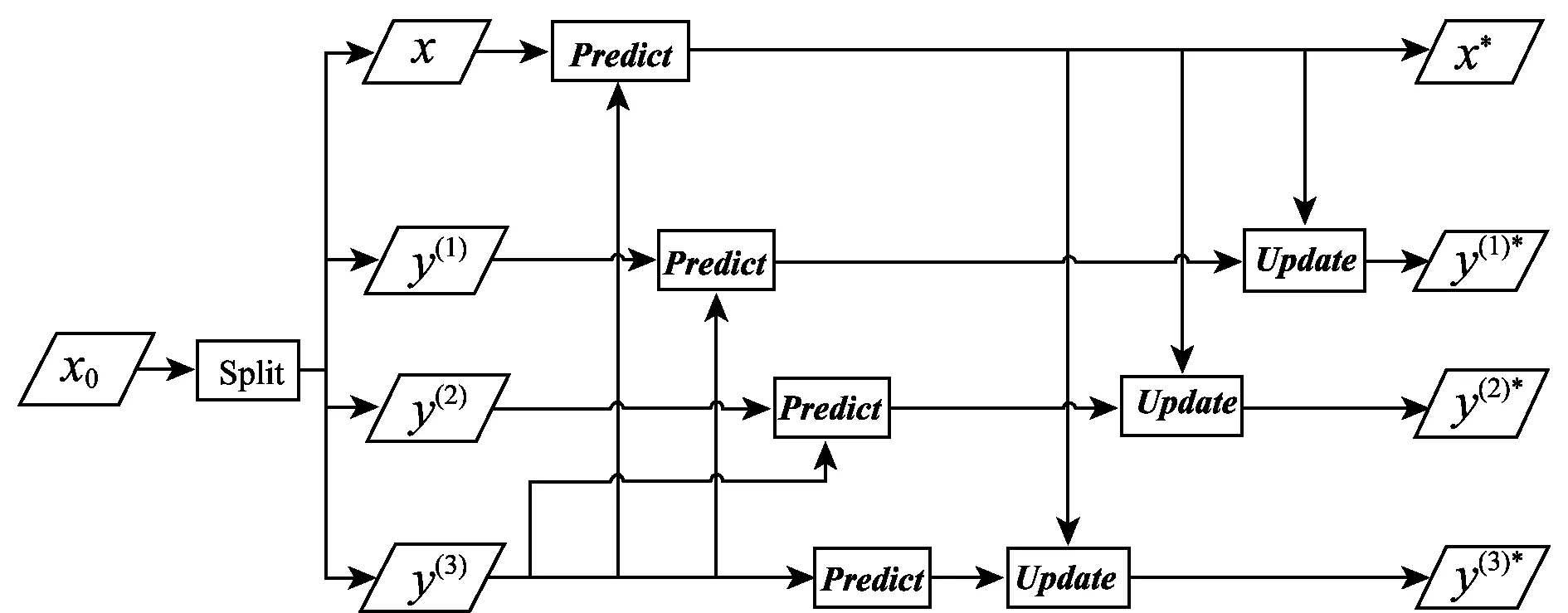
图1 图像的提升小波分解过程Fig.1 Lifting wavelet decomposition process of image

(3) 重构形式，即

(12)

(4) 将近似信号x(m,n)和细节信号y(1)(m,n),y(2)(m,n),y(3)(m,n)合并成原始信号x0。

(13)

3 融合规则

对于小波分解后的低、高频系数的融合,目前主要有基于单个像素的融合规则和基于区域的融合规则[10-15]。基于单个像素的融合规则有较快的计算速度,但没有考虑图像像素的相关性,众所周知,图像中的目标是以区域的形式存在的,据此,对图像作不可分提升小波分解后的低、高频图像都采用基于区域的融合规则。传统的低频图像是采用加权平均的融合规则,这种融合策略会削弱图像前景和背景的差别,从而会使对比度降低,为了突显图像中的目标和特征,本文对分解后的低频图像采用的融合规则为区域方差取大的方式;而小波变换的高频子图像很好地体现了图像中目标的边缘轮廓。据此,本文对图像的高频成份的融合规则采用基于区域能量取大的方式。图2描述了本文方法的实现过程,以下为算法描述步骤。

步骤1使用本文构造的P(x,y)对参加融合的两幅图像进行逐层分解。

步骤2融合分解得到子图像。

(1) 对于低频部分,方差是一个反差(对比度)的测度,它能反映图像中目标与背景的差别,为了体现低频信息中的图像目标,提高融合结果图像的对比度,这里采用局部方差取大的融合规则,设图像A分解后的低频子图像为Aj,l(l表示低频,j表尺度),图像B分解后的低频子图像为Bj,l,Aj,l中以(m,n)为中心的3×3窗口的局部方差为δAj,l(m,n),而Bj,l中对应位置窗口的局部方差为δBj,l(m,n),融合后低频子图Fj,l的像素在(m,n)点的值为

对所有的m,n

(14)

对所有的m,n

(15)

步骤3对所得结果进行不可分提升小波的逆变换,重构融合后的图像。

图2 本文方法的多聚焦图像融合过程Fig.2 Process of multi-focus image fusion based on the proposed fusion method

4 实验结果及分析

4.1 实验结果

为了验证本文方法的性能,对本文方法进行了大量的实验比较和分析研究,得到了一致的结论。图3列出3对实际多聚焦图像的融合结果,并展示其客观评价。

图3 3对多聚焦图像Fig.3 Three pairs of multi-focus images

为了体现的本文融合方法的性能,把本文提出的基于二维四通道不可分小波的融合方法与张量积小波的融合方法、张量积提升小波的融合方法、轮廓波的融合方法进行比较,4种方法采用相同的融合规则,图像分解层数均为3层,为使得4种参与比较的方法的滤波器大小一致,基于张量积小波融合方法所选用的是Daubechies系列小波的第2个小波,即db2小波,张量积提升小波是db2小波的提升小波。实验在Matlab 7.8中编程实现。图4(a)、图5(a)、图6(a)为基于张量积小波融合方法的结果图像,图4(b)、图5(b)、图6(b)为基于张量积提升小波融合方法的结果图像,图4(c)、图5(c)、图6(c)为轮廓波融合方法的结果图像,图4(d)、图5(d)、图6(d)为本文方法的融合图像,各种方法均对图像进行3层数分解。

从融合的视觉效果可以看出,本文方法融合结果图像的左右两边都很清晰。为了更加清楚地比较4种方法的视觉效果,提取图4、图5、图6中12幅结果图像的边缘,对它们的清晰度进行对比。图像边缘信息越丰富,表明图像细节信息更丰富,从而图像越清晰。据此,使用能提取丰富边缘信息的Canny算子提取各种融合结果图像的边缘图。图7(a)～7(d)分别是图4(a)～4(d) 4幅图像的边缘图,图8(a)～8(d)分别是图5(a)～5(d) 4幅图像的边缘图,图9(a)～9(d)分别是图6(a)～6(d) 4幅图像的边缘图。通过图7～图9中红色圆圈标记处的比较可以看出,本文方法的融合结果比张量积小波融合方法、张量积提升小波融合方法、轮廓波融合方法在结果图像的边缘处细节保持得更加完整,细节表现力更强,从而图像更清晰。

图4 Pepsi融合结果图像Fig.4 Fusion result image of Pepsi

图5 Clock融合结果图像Fig.5 Fusion result image of Clock

图6 Book融合结果图像Fig.6 Fusion result image of Book

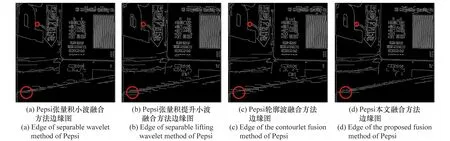
图7 Pepsi边缘对比图Fig.7 Edge contrast diagram of Pepsi

图8 Clock边缘对比图Fig.8 Edge contrast diagram of Clock

图9 Book边缘对比图Fig.9 Edge contrast diagram of Book

为了进一步展示本文融合方法所得融合结果图像的清晰度,对比本文方法与张量积小波融合方法、张量积提升小波融合方法、轮廓波融合方法的结果图像的直方图,直方图的分布范围越宽,图像越清晰,分别求取本文融合方法结果图像的直方图与其他3种融合方法的直方图的差,差值大于0,则表明本文方法所在灰度级的像素数比其他方法的相应灰度级的像素数多,若差值直方图在原图像的最小值的左边或最大值的右边局部范围出现正值偏多,则表明被减直方图所对应的图像在最大值或最小值处的像素更多,从而拉开了诸多像素前景和背景的差距,从而图像清晰度更高。以Pepsi融合图像为例,图10(a)、图10(b)、图10(c)分别是本文方法分别与其他3种方法融合结果图像直方图求差后所得的结果,可以看出本文方法与张量积小波融合方法、张量积提升小波融合方法和轮廓波融合方法所得结果图像的直方图的差在图像最大值和最小值局部处(见图10中红色框处)有更多的像素分布。由此说明本文融合方法有较高的清晰度。

图10 Pepsi直方图差值对比图Fig.10 Histogram difference contrast diagram of Pepsi

4.2 融合效果客观评价

假设融合结果图像用F表示,图像大小为M行N列。为了衡量图像的融合效果,本文采用以下几个指标:

(1) 清晰度(image definition, ID)

清晰度是用来衡量图像是否清晰的重要量化指标,定义式为

(16)

式中,ΔFx和ΔFy分别表示图像F在x和y两个方向的差分。ID越大,表示图像越清晰。

(2) 熵(entropy, E)

熵反映图像携带信息的丰富程度,定义式为

(17)

式中,L表示图像的灰度级数；p(i)表示灰度级为i的像素的概率。E越大,表示图像所含信息越多。

(3) 平均梯度(average gradient, AG)

平均梯度通过图像微小细节反差变化的速率来实现对图像的清晰程度的评价。定义式为

(18)

一般来说,AG越大,表示图像的层次越多,图像就越清晰。因此可以用AG来评价融合结果图像在微小细节的表达能力上的差异。

(4)标准差(standard error, SD)

标准差反映图像灰度相对于均值的离散情况,定义式为

(19)

SD越大,图像的灰度级分布的就越分散,图像的前景灰度值与背景灰度值相差就越大,图像就越清晰。

表1、表2和表3分别列出了Pepsi融合图像、Clock融合图像和Book融合图像这3组实验的各项指标的值。比较表1～表3中各列数据可以看出,第4行数据的值比第1行、第2行、第3行的值都大,从而说明本文提出的融合方法的各项指标高于张量积小波融合方法、张量积提升小波融合方法以及轮廓波融合方法的各项相应指标,因此本文方法的融合图像有较高的清晰度和空间分辨率,融合效果更好。

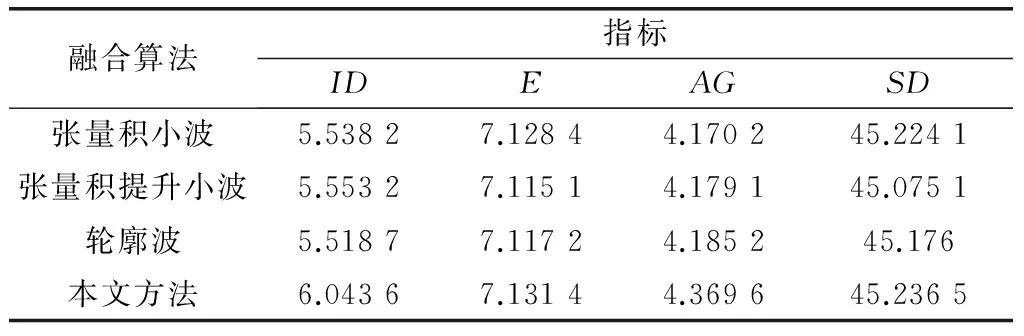
表1 Pepsi图像客观性能比较

表2 Clock图像的客观性能比较

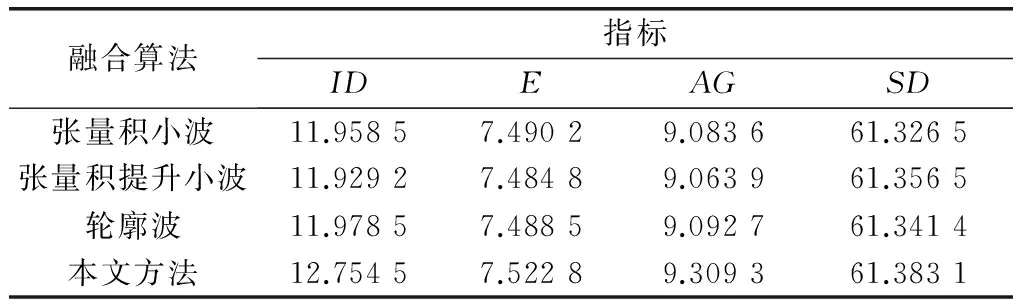
表3 Book图像的客观性能比较

与二维四通道不可分小波融合方法相比,本文提出的融合方法在速度上有着明显的优势。对于这2种融合算法而言,包括分解、融合、重构3个部分,分解与重构互为逆过程,融合采用相同的融合规则,因此通过比较2种算法的1层分解过程的算法复杂度来确定2种方法的融合速度,多层分解可类似地计算其复杂度。分解和重构过程中运算主要包括乘法和加法两种,因为加法的运算量远小于乘法,所以以其中的乘法运算量作为最终计算的复杂度,下面计算2种算法的算法复杂度。

假设源图像大小为M×N,对于不可分小波而言[16],选择L×L大小的滤波器组(矩阵)进行卷积,可计算其算法复杂度为

On=4×L2×M×N

(20)

对于本文建议的不可分提升小波而言,按照式(11)计算算法复杂度,每进行一次提升分别经过2次预测更新,预测过程中可计算算法复杂度为Op=5×M×N,更新过程中因为三角化矩阵的更新算子的对角线全为1,所以更新的算法复杂度为Ou=3×M×N,因而一层提升分解方案的算法总的复杂度为Ol=8×M×N。以本文中的实验方案为例,此时滤波器大小为4×4,即L=4,因此,On=64×M×N,是Ol大小的8倍,因而实现了不可分小波的快速提升,从而也提高了图像融合的速度。

5 结 论

本文利用矩阵分解方法,设计了二维四通道不可分小波滤波器组,提出了其提升方案,并把它应用于图像融合中,提出了一种基于二维四通道不可分小波提升方案的多聚焦图像的融合方法。从融合的视觉方面看,本文方法可以提取更多的细节信息,使得图像更加清晰。从融合的客观性能看,与张量积小波融合方法、张量积提升小波融合方法及轮廓波融合方法相比,本文方法有较高的清晰度、平均梯度、熵值和标准差;与提升之前的二维四通道不可分小波融合方法相比,本文方法有较快的融合速度。

[1] POHL C, VAN GENDEREN J L. Review article multisensor image fusion in remote sensing: concepts, methods and applications[J].International Journal of Remote Sensing,1998,19(5): 823-854.

[2] XU H, WANG Y, WU Y J, et al. Infrared and multi-type images fusion algorithm based on contrast pyramid transform[J]. Infrared Physics & Technology, 2016, 78: 133-146.

[3] 刘斌, 乔双梁, 魏艳萍. 基于采样三通道不可分小波的多光谱图像融合[J]. 仪器仪表学报, 2015, 36(3): 645-653.

LIU B, QIAO S L, WEI Y P. Multi-spectral image fusion method based on subsampled three channel non-separable wavelets[J]. Chinese Journal of Scientific Instrument, 2015, 36(3): 645-653.

[4] 李凯,刘斌.非下采样三通道不可分小波的多聚焦图像融合[J].计算机工程与应用, 2012, 48(17): 174-177.

LI K, LIU B. Multi-focus image fusion based on nonsubsampled three-channel non-separable wavelets[J]. Computer Engineering and Applications, 2012, 48(17): 174-177.

[5] ZHAO C, PU H, WANG B, et al. Fusion of hyperspectral and multispectral images: a novel framework based on generalization of pan-sharpening methods[J]. IEEE Trans.on Geoscience and Remote Sensing Letters, 2014, 11(8): 1418-1422.

[6] DAUBECHIES I, SWELDENS W. Factoring wavelet transforms into lifting steps[J]. Journal of Fourier Analysis and Applications, 1998, 4(3): 247-269.

[7] CHEN Q H, MICCHELLI A C, PENG S L, et al. Multivariate filter banks having matrix factorizations[J]. SIAM Journal on Matrix Analysis and Applications, 2003, 25(2): 517-531.

[8] XU X, WANG Y, CHEN S. Medical image fusion using discrete fractional wavelet transform[J]. Biomedical Signal Processing and Control, 2016, 27: 103-111.

[9] ZHANG Y, BAI X Z, WANG T. Boundary finding based multi-focus image fusion through multi-scale morphological focus-measure[J]. Information Fusion, 2016, 35: 81-101.

[10] 李光鑫,王珂.基于Contourlet变换的彩色图像融合算法[J]. 电子学报, 2007, 35(1): 112-117.

LI G X, WANG K. Color image fusion algorithm using the contourlet transform[J].Acta Electronica Sinica,2007,35(1): 112-117.

[11] 徐小军, 王友仁, 陈帅. 基于下采样分数阶小波变换的图像融合新方法[J]. 仪器仪表学报, 2014, 35(9): 2061-2069.

XU X J,WANG Y R, CHEN S. Novel image fusion method based on down sampling fractional wavelet transform[J]. Chinese Journal of Scientific Instrument,2014,35(9):2061-2069.

[12] VIVONE G, RESTAINO R, MURA M D, et al. Contrast and error-based fusion schemes for multispectral image pansharpening[J].IEEE Geoscience & Remote Sensing Letters,2014,11(5): 930-934.

[13] TAO G G, LI D P, LU G H. On image fusion based on different fusion rules of wavelet transform[J]. Aata Photonica Sinica, 2004, 33(2): 221-224.

[14] ZHAO J F, CUI G M, GONG X L, et al. Fusion of visible and infrared images using global entropy and gradient constrained regularization[J]. Infrared Physics & Technology, 2017, 81: 201-209.

[15] YU N N, QIU T S. Fusion technology of infrared and visible image in compressive sensing[J].Signal Processing,2012,28(5): 692-698.

[16] LIU B, LI K, LIU W J, et al. Construction method of three-channel non-separable symmetric wavelets with arbitrary dilation matrices and its applications in multispectral image fusion[J]. IET Image Processing,2013,7(7):679-685.