基于聚合算法的失效相关多部件系统维修策略优化
姚运志, 孟 晨, 王 成, 李宝晨
(1. 陆军工程大学石家庄校区导弹工程系, 河北 石家庄 050003; 2. 陆军工程大学科研部, 河北 石家庄 050003)
0 引 言
随着科技的不断发展及其在制造业的应用,设备的功能日益丰富,结构也日趋复杂。在设备的设计阶段,多部件系统因其功能强大,结构紧密而受到设计者的青睐。然而,这也对设备的维修提出了更高的要求[1]。对于多部件系统,由于部件间失效相关(含经济相关、结构相关)的广泛存在,针对单部件的维修策略不再适用,科学合理的维修策略的制定难度大增。从20世纪80年代起,针对部件间失效相关的问题,国内外学者展开了一系列研究[2-5]。
早期的研究偏重于对失效相关的描述与建模,近年来,基于失效相关的模型描述,研究的重心向维修策略倾斜。在文献[6]中,选择随机关联系数来描述部件间的相关性,各部件之间的失效相关性受时间影响。文献[7]认为系统中某部件的失效会使其他关联部件失效率提高。文献[8-9]针对结构复杂的系统,对其部件间的失效相关进行建模分析。国内学者在多部件系统维修策略的研究上也倾注了更多的精力。文献[10]以两部件系统为基础,用关联系数描述故障相关性,构建维修费率函数,讨论了多部件系统预防维修策略问题。文献[11]针对两部件系统,以最低系统期望成本率为目标,研究了预防性维修与机会维修相结合的维修策略。文献[12]综合考虑时间相关、结构相关、功能相关,对成组维修策略进行优化。目前的研究存在以下问题:①现有文献侧重于多部件系统维修策略优化的方法提出及模型建立,对具体求解方法讨论较少;②现有模型对于失效相关和经济相关没有同时定量的描述;③没有一个科学合理的方法来描述部件状态迁移对其他部件的影响;④对于考虑失效相关与机会维修的多部件系统维修策略问题,现有的方法还不能给出具体的求解方法。
基于以上分析,本文在综合考虑失效相关和经济相关的基础上,从建模和求解算法两方面展开研究,为多部件系统维修策略优化提供了一种新的可行方案。本文的创新性贡献为:①同时定量地考虑了失效相关和经济相关;②使用转移概率矩阵定量描述部件状态迁移对系统中其他部件状态的影响;③采用聚合迭代算法实现了对模型的求解,并对正确性和收敛性给出了严格的数学证明。
1 多部件系统折扣准则模型
马尔可夫过程的优化准则主要包括折扣准则、平均准则和总报酬准则等。折扣准则是以最小化折扣总成本为优化目标,更适用于维修决策模型的建立。本文基于折扣准则,建立多部件系统折扣准则模型,得到系统的最小折扣总成本。
1.1 模型假设
为明确多部件系统维修模型的适用对象,给出以下假设:
(1) 每个部件的劣化过程服从连续时间的马尔可夫过程;
(2) 通过状态监测可得到系统中每个部件的状态;
(3) 系统中各部件存在失效相关,即某部件的失效会导致其他部件的失效或劣化速度提高;
(4) 系统中各部件存在经济相关,即同时对多个部件进行维修的成本低于单独维修各部件的成本的代数和;
(5) 为切于实际,部件的预防性维修成本低于修复性维修成本,部件的运行成本低于维修成本。
(6) 维修过程中不会使系统的状态发生迁移;
(7) 两个连续的维修决策时刻之间不会发生部件的状态迁移。
1.2 模型建立

为便于连乘运算与求和运算的书写,用xi和yi分别表示部件i的两种状态(xi和yi与上一段中xi意义相同)。若系统中只有部件i失效,则用Hi(yi|xi)表示部件i由状态xi到yi转移概率,对应的转移概率矩阵为Hi。若系统中存在其他部件失效,则用Qi(yi|xi)表示部件i由状态xi到yi转移概率,对应的转移概率矩阵为Qi。
多部件系统的一步状态转移矩阵可表示为
其中
Pr(yi|xi,ai)=
(1)


(2)

(3)
式中,cc和cs分别表示系统运行的可变成本系数和固定成本,cs>0。系统运行的可变成本与系统状态相关,cc反映了系统在不同状态下运行成本差异的程度,其值越大则差异越大,系统状态对运行成本的影响越大。
(4)

(5)
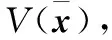


(6)
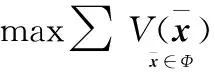

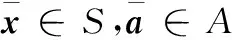
(7)
此线性规划问题的最优解为

式(6)、式(7)求解的目标是一致的,即对失效相关的多部件系统中的每一个部件选择合适的维修行为,在保证系统可靠性的前提下,使得维修成本最低(得到最小折扣总成本)。得到最小折扣总成本的维修行为组合,称之为最优维修策略。最优维修策略A*可以这样描述:
对于式(7)中的线性规划问题,当规模较小时,很容易解决。但是,若问题的规模很大时,计算量以及所需的内存空间及计算时间都难以承受。为此,提出下述算法,通过聚合的方法将问题的规模变小,并运用迭代的方法求其最优解。
2 聚合迭代算法
本节提出的聚合迭代算法将较大规模的线性规划问题集合成一个较小规模的聚合线性规划问题,计算得到后者的最优解后,再通过分解的方法将其分解成原线性规划问题的近似解,然后以此近似解作为聚合步骤的参数重新进行“聚合-分解”得到新的近似解,经过有限次迭代,使近似解收敛到原问题的最优解。最后以此最优解求出最优维修策略。
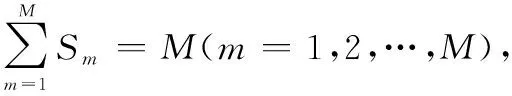
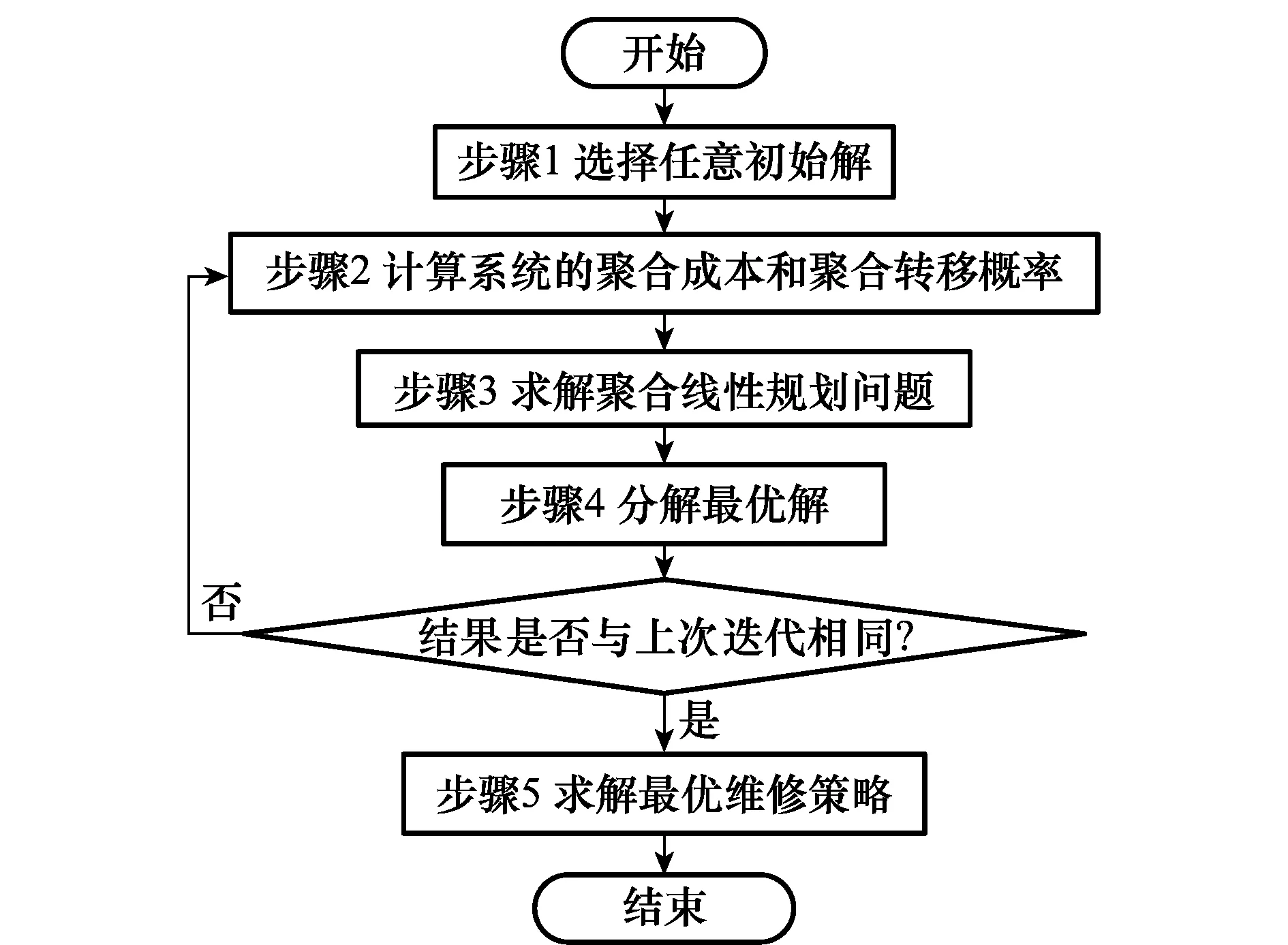
图1 聚合迭代算法流程图Fig.1 Flow chart of iterative algorithm

步骤2以第t次迭代得到的结果为参数聚合原线性规划问题(7):
m=1,2,…,M;k=1,2,…,K
(8)
l=1,2,…,M
(9)

m=1,2,…,M;l=1,2,…,M;k=1,2,…,K
(10)
步骤3求解问题(11),得到t+1次迭代的聚合最优解。
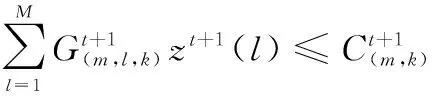
m=1,2,…,M;k=1,2,…,K
(11)
步骤4分解步骤3中得到的最优解,得到以下变量:
(12)
若变量
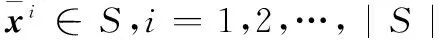
(13)

步骤5计算最优维修策略。

(14)
在步骤4中,为保证算法的收敛性,使用了非线性算子T,T对V运算定义为
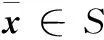
(15)
(16)


m=1,2,…,M
(17)

(18)


(19)
由于不满足不等式(13),则
(20)
证毕
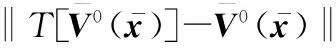

(21)
由于线性算子T为压缩映射,所以有式(22)成立。
0<α<1
(22)


由不等式(13)可知不等式(23)成立
(23)
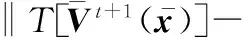
证毕
3 数值算例
本节给出两个数值算例,用以说明失效相关程度对折扣总成本以及最优维修策略的影响,探究多部件系统折扣准则模型中成本参数对最优维修策略的影响。
3.1 失效相关程度对折扣总成本及最优维修策略的影响
当系统中各部件存在失效相关,维修成本在总成本中占有较高比重时,失效相关程度越高,折扣总成本也就越高,相应的最优维修策略相对于无失效相关时的维修策略,差异也就越大。为了说明这一结论,给出以下3种情况。
情况1系统中各部件不存在失效相关,Hi=Qi,对∀i∈{1,2,…,n};
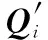

假定系统由6个劣化特性(包括劣化状态分级、失效对其他部件的影响等与本文计算模型相关的参数)相同的部件组成(U1~U6),采用文献[10]中的方法,基于失效相关多部件系统的实际数据,对解析模型中的相关参数进行拟合求解,进而得到相关的成本参数。本文设定的成本参数和转移概率矩阵见表1和表2,设维修费用的单位为“1”。为简化分析,考虑到假定的维修成本占系统总成本比重较高,这里将系统运行成本暂时忽略不计。
下面应用聚合迭代算法对上述情况的最优折扣总成本V*和最优维修策略A*进行计算。最优折扣总成本的计算结果如表3所示,由此可得到以下结论。

表1 维修成本参数

表2 转移概率矩阵

表3 最优折扣总成本


(2) 对∀i,j∈{1,2,…,n},当i 上述分析表明,若系统中存在失效相关,当系统运行成本相对于维修成本较小且系统规模较大时,考虑失效相关制定的维修策略能显著降低维修成本,降低的程度随着失效相关性的增强而提高。 图2 转移概率矩阵为Qi和时的维修成本增加比率Fig.2 Increase ratio of maintenance cost when transfer probability matrices are Qi and 表4 维修成本参数 (1)c0对最优折扣总成本的影响 图3 不同c0下的V*与Fig.3 V* and when c0 changes (2)cf与cp对最优折扣总成本的影响 图4 不同cf下的V*与Fig.4 V* and when cf changes (3)cs对最优折扣总成本的影响 图5 不同cp下的V*与Fig.5 V* and when cp changes 图6 不同cs下的V*与Fig.6 V* and when cs changes (4)cc对最优折扣总成本的影响 图7 不同cc下的V*与Fig.7 V* and when cc changes 本节探究应用聚合迭代算法与直接求解式(7)中的线性规划问题在计算耗时和占用内存上的差别。实验参数设定同第3.1节,将系统中部件数量从3个逐渐增加至9个。实验运行在Intel Core i5-3210M(2.50 GHz, 2.50 GHz)CPU上,计算机RAM为8GB,操作系统为64位Windows 7,算法运行在Matlab上。实验结果如表5所示。 表5 两算法计算耗时与占用内存的对比 本文在考虑失效相关与经济相关的基础上,从建模和求解算法两个方面研究了多部件系统的维修策略优化问题。首先建立多部件系统的折扣准则模型,进而将维修策略方程转化为线性规划问题,利用聚合迭代算法对其进行简化并求解,最后通过数值算例,说明了失效相关程度对折扣总成本以及最优维修策略的影响,探究了多部件系统折扣准则模型中成本参数对最优维修策略的影响。实验结果显示,采用聚合迭代算法可以有效提高运算速度,降低内存占用。 [1] BENOIT L, PHUC D, ERIC L, et al. Opportunistic maintenance based on multi-dependent components of manufacturing system[J].CIRP Annals-Manufacturing Technology,2016,65(1):401-404. [2] HEPING L, ESTELLE D, LAURENCE D. A condition-based maintenance policy for multi-component systems with Lévy copulas dependence[J].Reliability Engineering and System Safety, 2016, 149(1): 44-55. [3] TOMASZ N, SYLWIA W. On problems of multi-component system maintenance modeling[J]. International Journal of Automation and Computing, 2009, 6(4): 364-378. [4] CHAN J, SHAW L. Modeling repairable systems with failure rates that depend on age and maintenance[J]. IEEE Trans.on Reliability, 1993, 42(4): 566-571. [5] WANG H, PHAM H. Some maintenance models and availability with imperfect maintenance in production systems[J]. Annals of Operations Research, 1999, 91(1): 305-318. [6] HONG H P, ZHOU W, ZHANG S, et al. Optimal condition-based maintenance decisions for systems with dependent stochastic degradation of components[J]. Reliability Engineering and System Safety, 2014, 121(1): 276-288. [7] GOLMAKANI H R, MOAKEDI H. Periodic inspection optimization model for a two-component repairable system with failure interaction[J].Computers & Industrial Engineering,2012,63(3): 540-545. [8] HUYNH K T, BARROS A, BERENGUER C. Multi-level decision-making for the predictive maintenance of k-out-of-n: F deteriorating systems[J].IEEE Trans.on Reliability,2015,64(1):94-117. [9] CANH V H, DO P, BARROS A, et al. Maintenance grouping strategy for multi-component systems with dynamic contexts[J]. Reliability Engineering and System Safety,2014,132(132):233-249. [10] 姚运志,孟晨,王成.考虑失效相关的多部件系统最优预防维修策略[J].计算机集成制造系统,2013,19(12):2976-2981. YAO Y Z, MENG C, WANG C. Optimal preventive maintenance policies for a multi-unit system considering failure interactions[J].The International Journal of Advanced Manufacturing Technology, 2013, 19(12): 2976-2981. [11] 张卓琦,吴甦,李斌锋.考虑故障相关的两部件系统机会维修策略[J].清华大学学报(自然科学版),2012,52(1):122-127. ZHANG Z Q, WU S, LI B F. Opportunistic maintenance policy for a two-unit system with failure interactions[J]. Journal of Tsinghua University (Science and Technology), 2012, 52(1): 122-127. [12] 杨元,黎放,侯重远,等.基于相关性的多部件系统机会成组维修优化[J].计算机集成制造系统,2012,18(4):827-832. YANG Y, LI F, HOU C Y, et al. Opportunistic group maintenance optimization of multi-unit system under dependence[J].The International Journal of Advanced Manufacturing Technology, 2012,18(4):827-832.


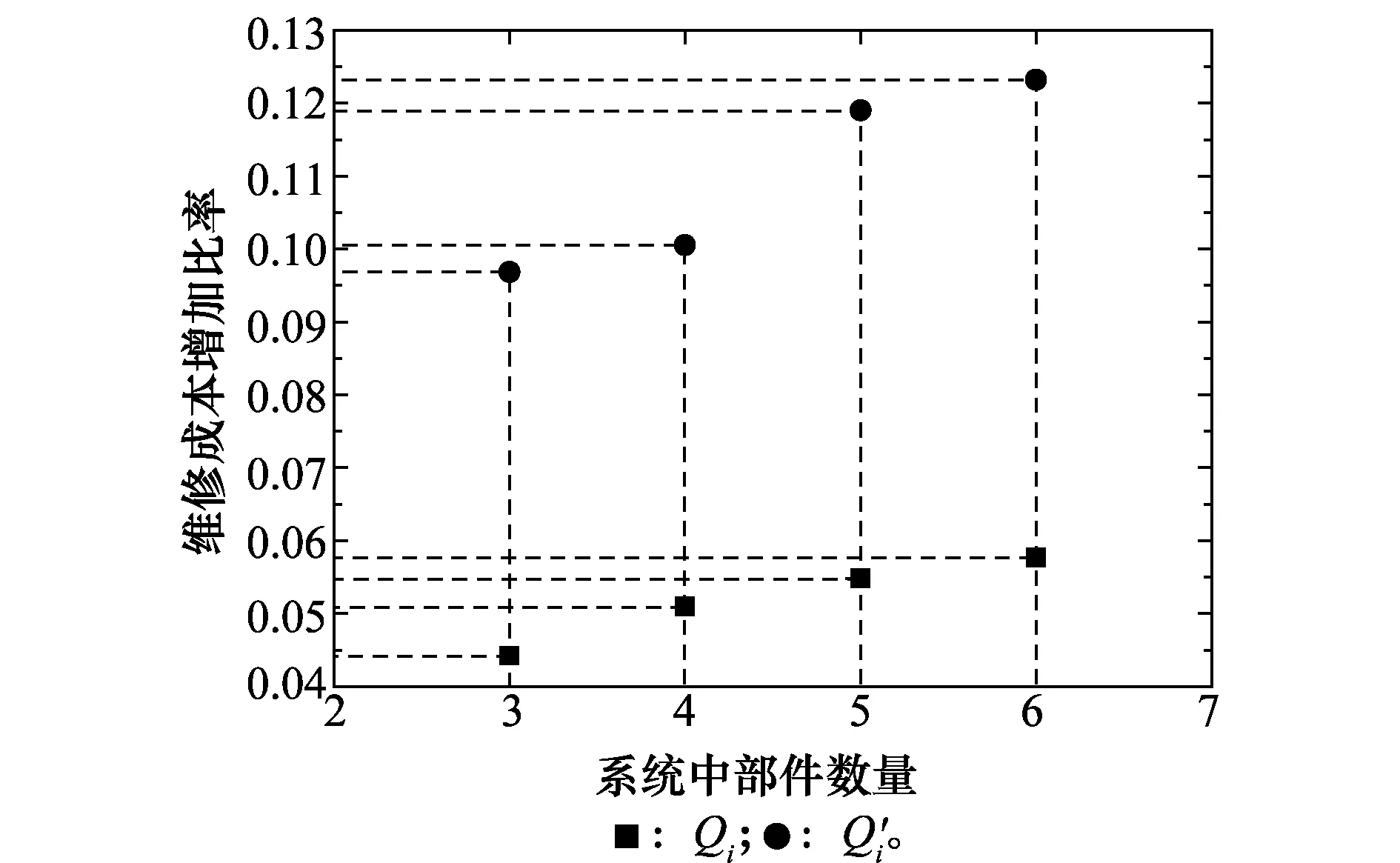
3.2 成本参数变化对最优折扣总成本的影响




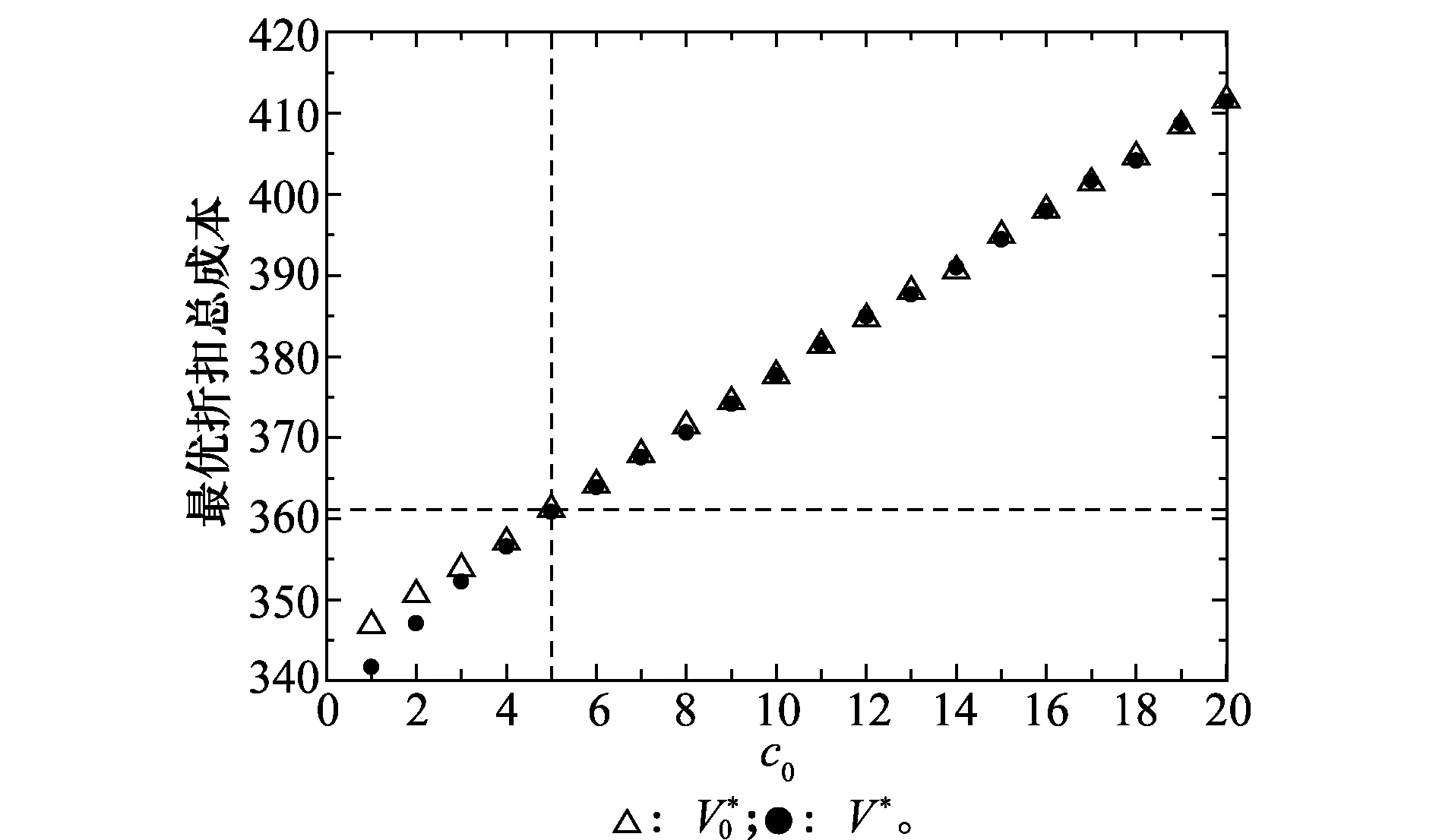

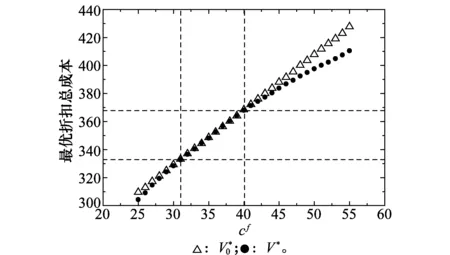





3.3 算法对比

4 结 论

