惯导误差下分布式雷达多目标空间配对算法

方 敏, 程子扬, 何子述, 李 军

(电子科技大学电子工程学院, 四川 成都 611731)

0 引 言

雷达组网是当前国内外在防空、进攻作战中已被采用的较先进的反侦探、反干扰,反隐身技术措施[1]。在分布式雷达组网中,每部雷达都可以作为一个完整的信息处理系统,利用组网雷达系统对同一目标的观测信息[2],可以提高对隐身目标的检测性能。为增强高速雷达平台的生存和协同作战能力,常采用惯导系统为平台提供定位功能。然而,在多目标的环境下,由于惯导误差的存在,使得组网雷达系统很难实现多目标的空间配对。因此可以看出,如何实现空域多目标的准确配对是多目标联合检测要解决的重要问题。

目标配对问题可以看成目标数据信息的关联问题,在分布式组网雷达体制下,常采用航迹关联的方法完成目标配对[3]。航迹关联的实质是判断来自不同雷达系统的航迹是否属于同一目标[4]。常用的航迹关联方法有最近邻域法,模糊函数航迹关联算法及模糊逻辑关联法[5-6]。航迹关联的前提是完成传感器空间配准,即需要准确地估计出传感器系统误差以校准目标航迹。文献[7]提出了一种基于滑窗法的极小化极大熵函数的传感器空间配准算法,该方法可以估计出传感器系统的偏差值,对其补偿后可以将目标的位置信息较准确地转换到共同坐标系下,由此分辨出不同目标完成目标的空间配对。但该方法只考虑了传感器距离、角度量测偏差,没有考虑惯导误差带来的平台定位误差,当存在较大的系统误差时,空间配准将十分困难以至于难以实现准确的数据关联[8]。为此,文献[9]提出了一种雷达组网配准前航迹关联算法,该方法不用事先校正和补偿组网雷达误差,虽然较传统处理方法关联概率有很大提升,但其正确关联概率仍然不高,在实际中应用不大。除此之外,目标配对问题在线性调频连续波(linear frequency modulated continuous wave,LFMCW)雷达体制下也做了许多研究。文献[10]在对称三角LFMCW雷达体制下,根据距离-速度耦合的现象和特点,提出了一种联合MTD通道检测结果与目标距离信息的方法实现上/下扫频段的目标配对。文献[11]提出了一种利用距离“局部航迹”信息和对同一目标上、下扫频段内“局部航迹”的相关性的目标配对算法。该方法在杂波环境、航迹交叉等复杂情况下能有效实现目标回波的有效配对。但上述方法都只是针对单基雷达,对于分布式组网雷达的目标配对问题,不同雷达对同一目标的观测数据都是非相参的,各雷达运动状态也都有所不同,因此都不能解决组网雷达体制下的多目标配对问题。针对分布式组网雷达体制,在大的惯导误差引起的雷达定位误差、雷达对目标量测存在误差的环境下,本文提出了一种直接利用雷达测量的目标斜距信息和多路径信息冗余的特性来实现多目标配对的方法,该方法不依赖于平台位置,因此,减小了惯导误差对配对的影响。由于该方法仅需利用斜距信息,因此,具有较高运算效率。最后,仿真结果验证该方法的有效性。

1 目标配对问题

图1 组网雷达及目标位置分布示意图Fig.1 Location of radar network and targets

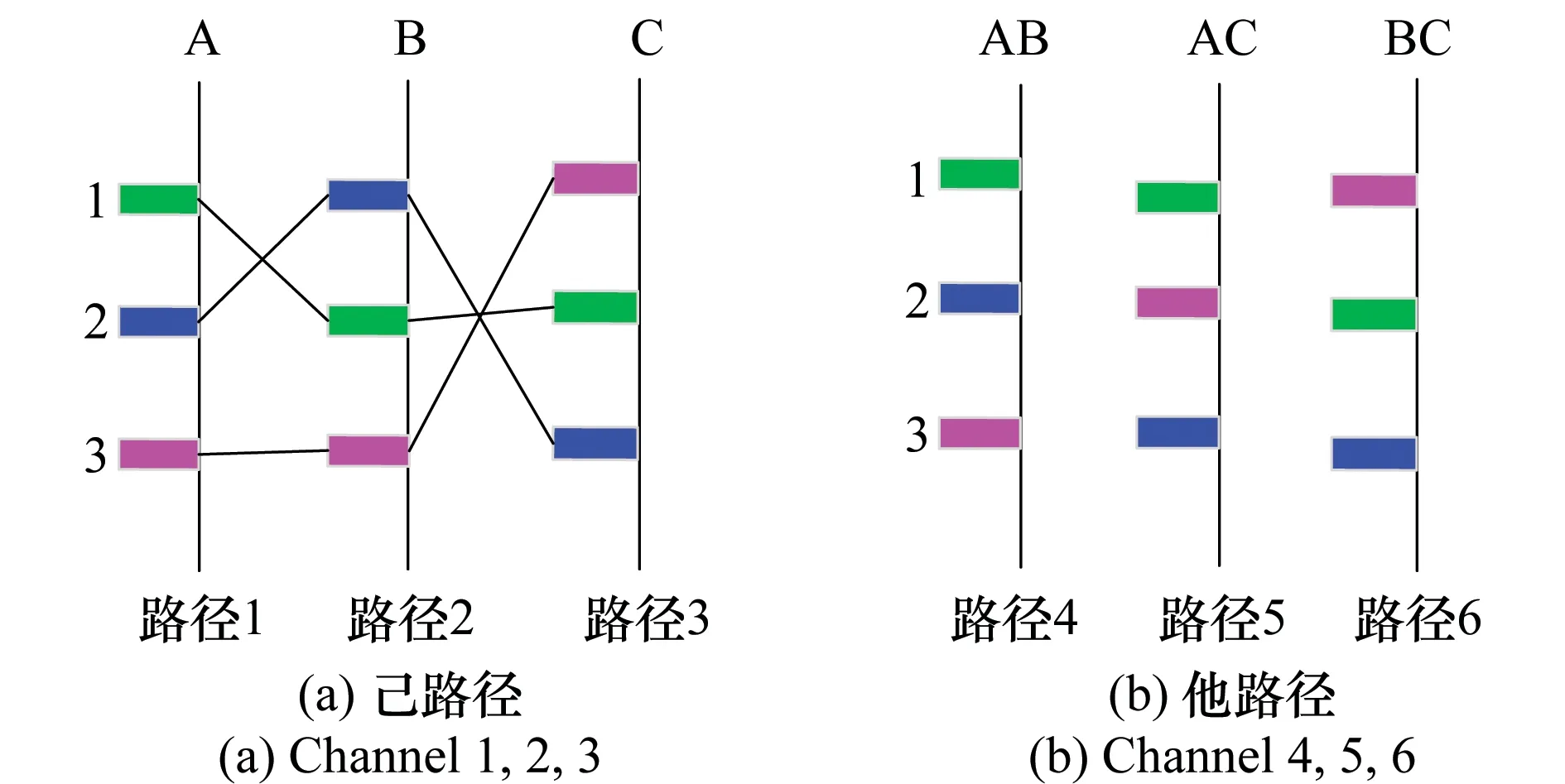
图2 目标配对及他路径示意图Fig.2 Targets pairing and channel 4, 5, 6

若要关联路径1上的目标q(q∈{1,2,3}),则以站A为球心,目标q到站A的距离为半径画球面:

(1)

式中,c=3×108m/s为光速。再在路径2与路径3上各选取一个目标,假设为目标m和目标n(m,n∈{1,2,3}),以类似的方式画球面。以其距离为半径画两个球面:

(2)

(3)

在实际情况中,雷达之间的间距相对于目标到各雷达的距离都很小,且目标分布在一个较小的区域,故联立方程(1)～方程(3)一定能解得3球面的两个公共交点p1(x1,y1,z1),p2(x2,y2,z2),如图3所示。

图3 三球相交示意图Fig.3 Intersection of three spheres

已知站A、站B位置和目标到两站的距离和,可以确定一个以A,B为焦点,长轴为目标到两站距离和的椭圆,以该椭圆所在平面作为参考平面,将其绕y轴旋转360°得到一个旋转椭球面,如图 4所示。有3个目标,可以确定3个椭球,若路径1,2选择的是同一目标,两交点必然在以该目标信息所画椭球面上。站AC、站BC同理。由此可知,当目标配对成功时,交点中存在真实目标,一定落在站AB、站AC、站BC对应的椭球面上,否则,目标配对失败。

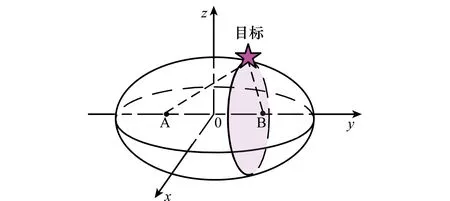
图4 站A,B与目标构成的椭球Fig.4 Ellipsoid described by radar A, B and target

2 目标配对算法

下面将按照上述思想实现目标配对。首先计算两交点p1,p2到站A、站B的距离和。这里,雷达站的位置为真实位置。虽然目前只有惯导系统给出的各站位置信息,但由于每个交点到任意两球心的距离和都等于两球面半径之和,即可以将交点到球心的距离用目标距离表示。由于后面计算只利用距离信息,故两交点任选一个即可,这里选p1。那么,p1到站AB、站AC、站BC的距离d1,d2,d3为

(4a)

(4b)

(4c)

(5a)

(5b)

(5c)

式中,i∈{1,2,3},表示目标编号。由此将目标配对问题用一组以目标距离信息和他路径信息构造的表达式代替。以下将分两种情况讨论:

(1) 若能找到一个i使式(5a)～式(5c)成立,则目标q配对成功,m=n=q;

(2) 若不能找到一个i使式(5a)～式(5c)成立,则路径1,2,3目标配对失败,需重新配对,重新选择m,n。针对配对失败这种情况,又可以分为以下两种情况:

失败情况1路径1,2,3中有两个路径选取到相同目标,即m,n中有一个为目标q。

失败情况2路径1,2,3中选到3个不同的目标,即m≠n≠q。

下面按照上述两种结果分析式(5a)～式(5c)的结果所对应的目标配对情况。

(1) 配对成功:当路径1,2,3配对成功时,即m=n=q,有

(6)

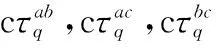
(2) 配对失败

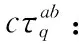
(7a)

而路径3选取了不同的目标,对任意i都有

(7b)

(7c)

情况2路径1,2,3都选取到不同的目标,即m≠n≠q。对任意i都满足:

(8)

即在所有他路径上,都不能找不到一个目标距离等于交点p1到AB,AC,BC的距离和d1,d2,d3。

上面的推导是在理想条件下,即斜距测量误差为0时进行的。然而在非理想条件下,斜距测量误差不可避免,故在路径1,2,3配对成功的情况下,不能严格满足式(8),但在门限ε内可以满足:

(9)

门限ε是一个可调参数,与己路径上最小目标距离差值Δmin和斜距误差δ有关,δ<ε<Δmin。Δmin的定义:

(10)

式中,下标编号i,j∈{1,2,3}表示目标；上标编号radar∈{a,b,c}表示雷达站。

同理,对配对不成功的两种情况也做相应的调整。

情况1路径1,2,3中有两个路径配对成功,即m,n中有一个为目标q。

假设m=q,路径1,2配对成功,对任意i,满足:

(11a)

(11b)

(11c)

情况2路径1,2,3中选到不同的目标,m≠n≠q。

对任意i,下式成立:

(12)

通过以上分析可以看出,虽然整个算法最开始的分析是在已知平台真实坐标位置信息的前提下,但从最后推导出的判别目标配对正确与否的表达式(5a)～式(5c)可以看出,该方法实际只与目标斜距有关,而与平台位置无关,这也恰好避免了平台位置误差所带来的影响。所以该方法不仅可以应用在存在平台位置误差的高速动态雷达组网上,对于雷达站位置精确已知的固定雷达组网同样适用。

2.1 目标配对步骤

根据以上分析,可以看出用来判断目标配对正确与否的表达式(5a)～式(5c)与平台位置信息没有关系,因此,对于大的惯导误差所带来的平台定位误差不影响该方法的性能。由此可以根据式(5a)～式(5c)的结果,设计相应的目标配对方法,算法步骤如下:

步骤1初始化:根据己路径上最小目标距离差值和斜距误差设置门限ε,从路径1,2,3中各选取一个目标,假设选取的目标依次为目标q,目标m和目标n;

步骤2根据式(4a)～式(4c)计算距离和d1,d2,d3;

步骤3利用他路径上各目标距离信息,计算式(5a)～式(5c),若满足式(9)则配对成功即m=n=q,进入步骤4,否则进入步骤5;

步骤4删除己路径上配对成功的目标,并判断路径1上的所有目标是否完成配对,若是则结束算法,否则从路径1上选择下一个目标进行配对,返回步骤2;

步骤5分情况讨论,若式(5a)～式(5c)的结果符合错误配对的情况1,对配对错误的路径重新选取目标,返回步骤2;若符合失败情况2,则任选一条路径重新选取目标,返回步骤2。

2.2 算法复杂度分析

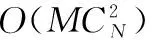
3 仿真实验

3.1 仿真1

雷达A,B,C的真实位置坐标分别为(0,0,20)km,(20,0,20)km,(0,20,20)km,3个目标的真实位置分别为(0,120,0)km,(2,120,0)km,(-2,122,0)km。惯导系统给出各个雷达的坐标分别(-0.153,1.985,18.317)km,(19.770，-1.573,21.847)km,(-1.982,21.100,21.269)km,坐标误差绝对值均小于2 km。实际系统测得的己路径、他路径上的时延所对应的目标距离信息,如表1和表2所示。雷达信号带宽为B=30 MHz,对应的距离分辨率为5 m。判决门限ε=12 m。由表1可知,单个己路径上的最小目标距离差值Δmin=16.4 m。

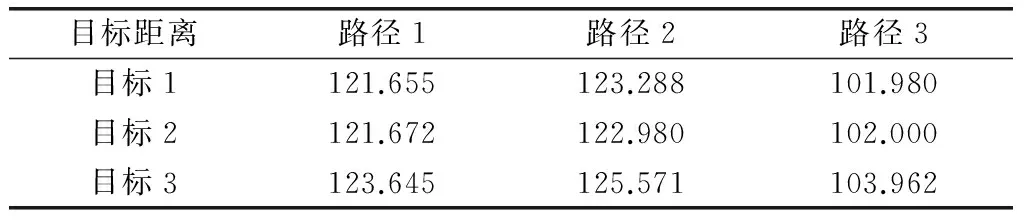
表1 己路径上各目标距离信息

表2 他路径上各目标距离信息

现对路径1,2,3任选目标进行配对仿真,分为3种情况,包括成功配对与失败配对两种情况。表3配对成功的情况,初始化路径1,2,3都选到目标1。表中2～表4每列数据分别代表d1,d2,d3与他路径上的各目标距离之差的绝对值。由表3可知,每条他路径上都能找到一个目标距离(目标1,红框标出)与d1,d2,d3的差的绝对值小于ε,满足式(9)。

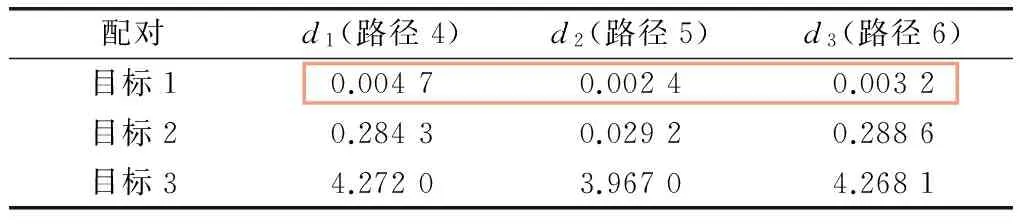
表3 配对成功

表4为配对失败情况1。其初始的配对情况为路径1,2选目标1,路径3选目标2。由表4中数据可知只有路径4上能找到一个目标距离(目标1,红框标出)与对应d1的绝对差值小于ε,而其他路径上的任意一个目标距离与对应d的绝对差值都大于ε,满足式(11a)～式(11c)。

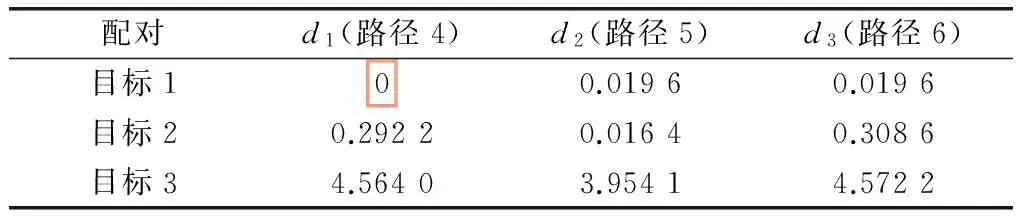
表4 配对失败情况1

表5为配对不成功的情况2。其初始的配对情况为路径1选目标1,路径2选目标2,路径3选取目标3。由表中数据可知所有路径上的任意一个目标距离与对应d的绝对差值都大于ε,满足式(12)。

表5 配对失败情况2

通过以上仿真可以看出,本文所推导的判断目标正确配对的表达式是可靠的,且表达式结果与目标配对情况和理论推导一致。

3.2 仿真2

在上述仿真参数下,图5和图6通过蒙特卡罗仿真得到所提方法的配对率随斜距误差,定位误差的变化情况,蒙特卡罗次数为1 000次。从图5可以看出,3种初始化情况下,该方法都能较好的完成多目标配对,即使在最坏情况下(失败情况2),配对率也能达到94%。其次,还能看出配对率随斜距误差的增大而减小。这是因为斜距误差越大,在一定门限下目标配对正确满足式(9)的可能性越小,故配对率降低。

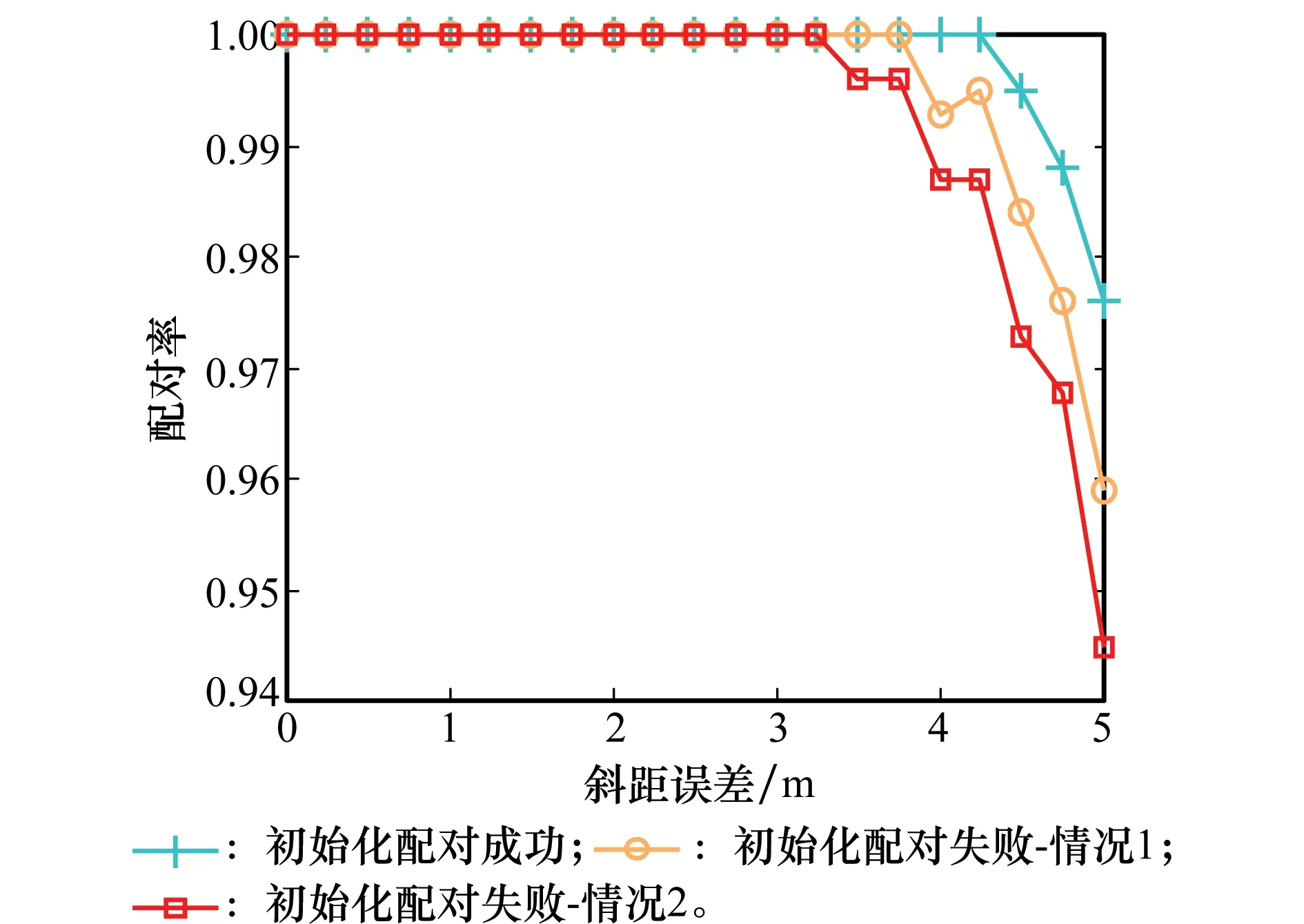
图5 配对率随斜距误差的变化图Fig.5 Target pairing rate with range error

图6仿真配对率随定位误差的变化情况,考虑最坏情况,即初始化时各己路径选择不同目标,固定斜距误差为5 m(引入不超过5 m的随机测量误差)。由图6可知,定位误差对该方法几乎没有影响,因此该方法弱化了大惯导误差对目标配对问题的影响。

图7通过蒙特卡罗仿真得到该方法在不同最小目标距离差值Δmin的情况下,配对正确率随斜距误差的变化情况,同样考虑最坏情况。由图7可知,在一定斜距误差范围内,所提方法能够实现目标的正确配对;其次当Δmin越小,配对率对斜距误差越敏感。这是因为当目标分布在相近距离单元时,从距离上分辨目标的难度加大,且越近,错误配对情况满足式(9)的可能性越大。只要根据最小目标距离差值Δmin,合理设置门限,在一定的斜距误差范围内还是能保证所提方法有效性。

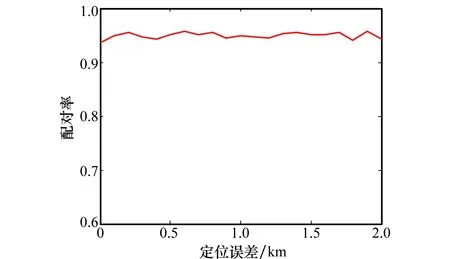
图6 配对率随定位误差的变化情况Fig.6 Target pairing with location error

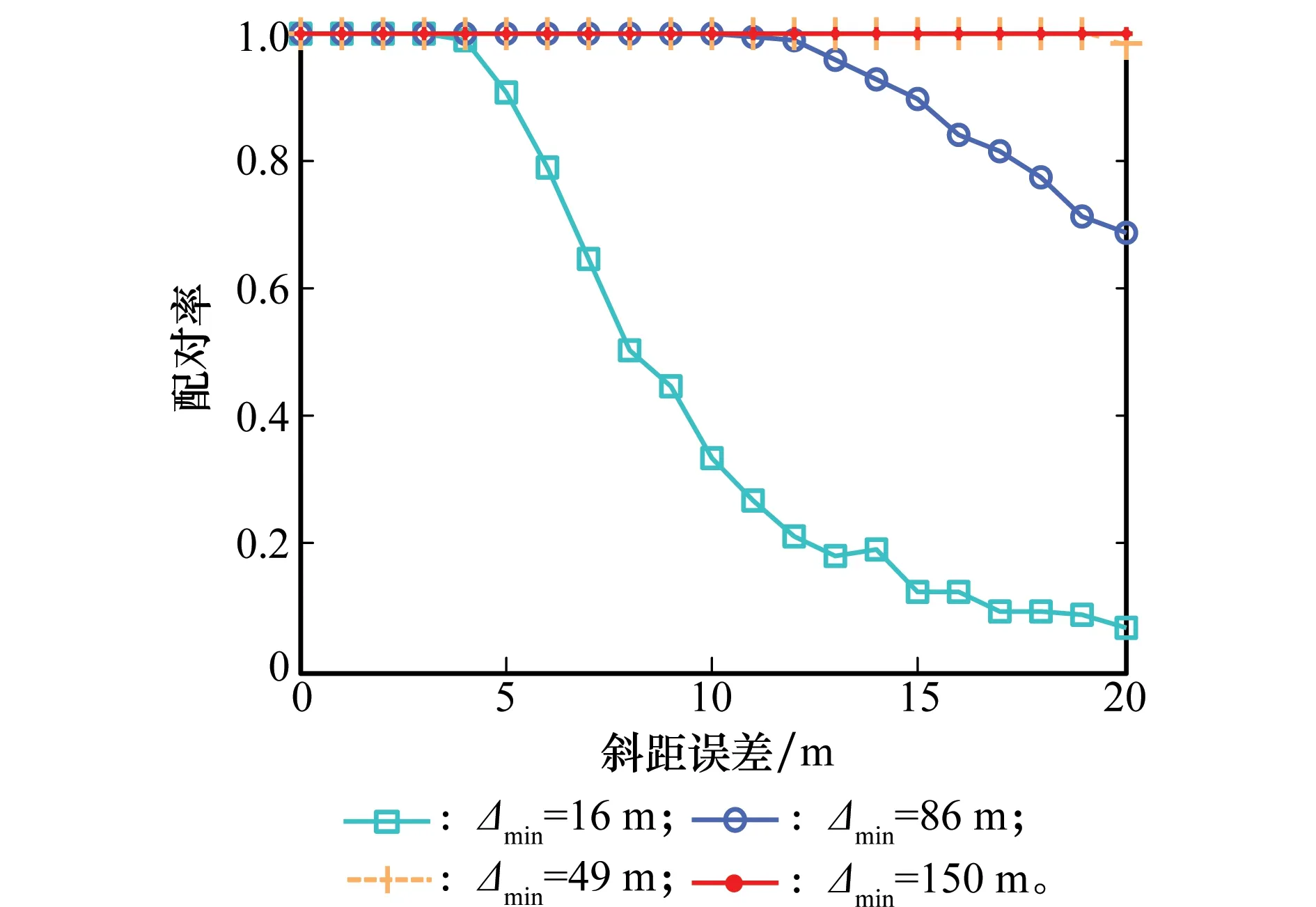
图7 不同Δmin下配对率随斜距误差的变化Fig.7 Target pairing with range error for different Δmin

从图7还可以看出当Δmin越小,本文方法效果越差。图8通过蒙特卡罗仿真实验得到Δmin=0时,3种初始化情况下配对率随斜距误差的变化情况,即对同一己路径,有两个及以上的目标分布在同一距离单元。由图8可知,在3种初始化情况下,所提方法已经无法完成目标配对。这是由于多目标分布在相同距离环时,已经无法从距离上区分不同的目标。

图8 Δmin=0,配对率随斜距误差的变化Fig.8 Target pairing rate with range error for Δmin=0

通过以上仿真分析可以看出,本文方法只利用了目标距离信息来完成目标配对,对于大惯导误差所带来的平台定位误差不会影响该方法的性能。其次,对于多目标环境,在单个己路径上,各个目标分布在不同距离单元位置上时,通过设置合适的门限,在一定斜距误差范围内,能够较好地完成多路径多目标配对。

4 结 论

当存在大惯导误差和测量误差时,如何实现多目标的正确配对是实现多目标联合检测的关键问题。本文针对这一问题提出了一种利用目标距离信息,结合多路径信息冗余特性的多目标空间配对方法。由于该方法只利用了目标距离信息,不需要雷达站位置信息,且不需要传感器配准就能实现目标配对,因此,对于大惯导误差所带来的平台定位误差并不会影响该方法的性能。最后,仿真实验分析了该方法的配对成功率随斜距测量误差和平台定位误差的变化情况。尽管本文的分析建立在3个雷达点的背景下,但该方法可以推广到3部以上雷达组成的分布式雷达组网系统的多目标配对情况。因此,具有很强的工程实用性。

[1] 王欢, 焦光龙, 谢军伟. 基于雷达组网中新 技术的研究[J]. 现代雷达, 2007(1):9-11,22.

WANG H, JIAO G L, XIE JW. Study on new technologies applied in radar network[J]. Modern Radar, 2007(1): 9-11,22.

[2] 石玥, 王钺, 周淑华. 雷达组网中联合数据关联与偏差估计方法研究[J].系统工程与电子技术,2006,28(11):1668-1671,1678.

SHI Y, WANG Y, ZHOU S H. Research on joint data association and bias estimation method in radar networks[J]. Systems Engineering and Electronics, 2006,28(11): 1668-1671,1678.

[3] 邵锡军, 周琳. 预警探测系统雷达组网技术研究[J].现代雷达, 2003(9):1-4.

SHAO X J, ZHOU L. Radar netting technology in early warning detection system[J]. Modern Radar, 2003(9): 1-4.

[4] 陈昌质,阮怀林.组网雷达系统中的一种模糊航迹关联方法[J].舰船电子对抗,2008(2):46-48.

CHEN C Z, RUAN H L. A fuzzy track correlation method netted radar system[J]. Shipboard Electronic Countermeasurein 2008(2): 46-48.

[5] 方青.雷达组网数据融合处理中的点迹融合技术[J].现代电子,2002(4):5-12.

FANG Q. Plot fusion technology in radar network data fusion[J]. Modern Electronics, 2002(4): 5-12.

[6] WIDE P. Fuzzy logic data correlation approach in multisensor-multitarget tracking system[J]. IEEE Trans. Signal Processing, 1999, 76(2):195-209.

[7] 郭军军, 元向辉, 韩崇昭. 采用熵函数法的多传感器空间配准算法的研究[J]. 西安交通大学学报, 2014(11):128-134.

GUO J J, YUAN X H, HAN C Z. A space registration algorithm for multi-sesor target tracking using an entropy function[J]. Journal of Xi’an Jiao Tong University, 2014(11): 128-134.

[8] 余安喜,杨宏文,胡卫东,等.基于相对系统误差估计的组网雷达点迹融合技术[J].系统工程与电子技术, 2003,25(9):1045-1048.

YU XI, YANG H W, HU W D, et al. Radar net contact fusion technique based on relative system error estimation[J].Systems Engineering and Electronics 2003,25(9): 1045-1048.

[9] 何友, 宋强, 熊伟. 基于傅里叶变换的航迹对准关联算法[J]. 航空学报, 2010(2):356-362.

HE Y, SONG Q, XIONG W. A track registration-correlation algorithm based on Fourier transform[J]. Acta Aeronautica et Astronautica Sinica, 2010(2): 356-362.

[10] 吴耀云, 罗飞腾, 陈卫东. 基于航迹关联的STLFMCW雷达多目标配对[J]. 系统工程与电子技术, 2008,30(6):1027-1031.

WU Y Y, LUO F, CHEN W D. Multi-target pairing for STLFMCW radar based on track correlation[J]. Systems Engineering and Electronics, 2008,30(6): 1027-1031.

[11] 张宏宇, 王冬华, 李云飞, 等. 一种提高LFMCW体制雷达测距精度的方法[J]. 雷达与对抗, 2017(1):9-12,47.

ZHANG H Y, WANG D H, LI Y F, et al. A method to improve the ranging accuracy of LFMCW radar[J]. Radar & ECM, 2017(1): 9-12,47.