基于多观测向量序列降采样恢复的稀疏矩阵重构
何兴宇, 童宁宁, 胡晓伟, 冯为可
(空军工程大学防空反导学院, 陕西 西安 710051)
0 引 言
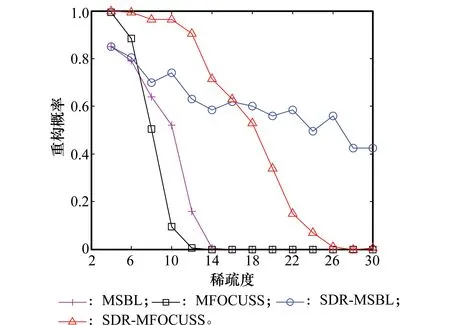
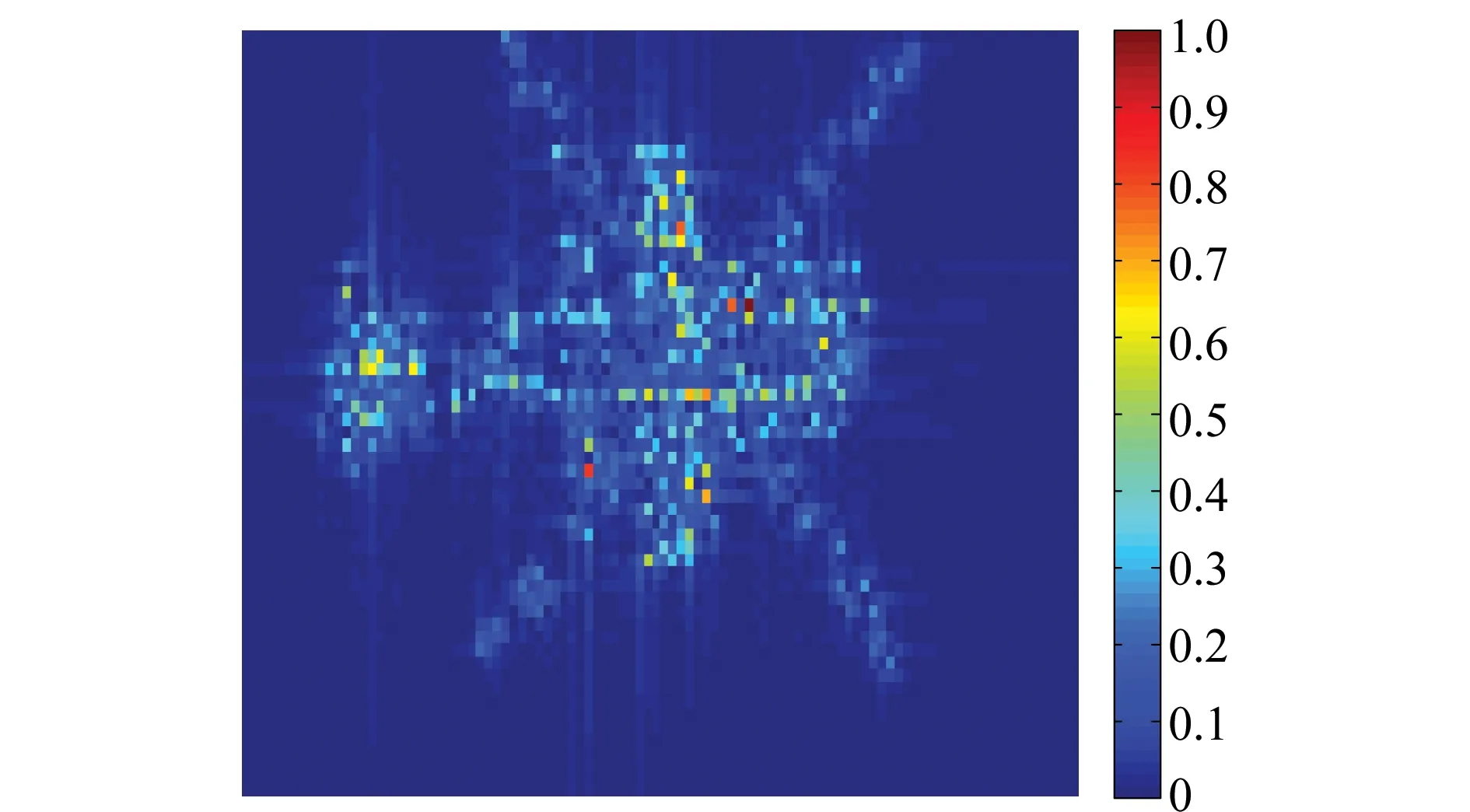
压缩感知(compressed sensing,CS)理论表明,大多数信号都有稀疏表示,这意味着信号可以通过少数信号在特定稀疏基下的系数来表示。稀疏信号可以通过远低于信号维度的观测信号来重构[1-2]。压缩感知的核心问题是:假设s是一个稀疏向量s∈Rn,通过观测矩阵A∈Rm×n和观测向量x=As来重构稀疏信号s。当m 由于目标函数‖·‖0是非凸的,所以很难找到0范数优化问题的最优解。一个比较有效的方法是,将上述0范数优化问题转换为它的凸近似,也即1优化问题,进而通过线性规划来找到其最优解。相比于0范数的优化问题,1范数优化问题表示的凸松弛问题可以更为有效地得到解决,并且得到的最优解与0范数优化问题一致。 很多基于单观测向量的重构算法可以拓展到多观测向量问题中。文献[4]表明,正交匹配追踪(orthogonal matching pursuit,OMP)算法在一定条件下可以找到多观测向量重构问题的稀疏解,文献[5]分析了该方法的性能。文献[6]研究了FOCUSS(focal underdetermined system solver)算法的拓展算法,分别提出了MFOCUSS(FOCUSS for multiple measurement vectors)算法和正则化MFOCUSS算法,来解决无噪声和有噪声情况下的多观测向量重构问题。文献[7]将稀疏贝叶斯学习(sparse Bayesian learning,SBL)算法拓展到多观测向量模型下,提出了稀疏贝叶斯学习的多维响应拓展(multiple response extension of SBL,MSBL)算法。然而,当矩阵中各个向量的非零元素的位置不同时,并且非零元素个数不是很少时,这些算法的重构误差将会很大,甚至失效。文献[8]基于SL0(smoothed L0)算法提出了一种2D-SL0(two-dimensional SL0)算法用于实现稀疏矩阵重构。该算法可以用于具有任意稀疏结构的稀疏矩阵重构。 为实现复杂稀疏结构的稀疏矩阵重构,本文构造了降采样矩阵,提出了一种基于多观测向量模型的序列降采样重构算法。仿真实验表明,通过提出的序列降采样方法(sequential down-sampling recovery algorithm, SDR)和MFOCUSS(SDR-MFOCUSS)算法,可以高概率地重构稀疏矩阵。基于序列降采样算法和MSBL(SDR-MSBL)算法同样有较好的性能,但是其计算量比SDR-MFOCUSS算法高很多。仿真实验同时表明,当降采样率较高时,所提出的SDR-MFOCUSS算法性能优于2D-SL0算法。基于目标逆合成孔径雷达图像的重构实验表明,所提算法能有效地实现具有二维稀疏特性的图像重构。 x(l)=As(l),l=1,2,…,L (1) 多观测向量模型可以表示为 X=AS (2) 式中,S∈Rn×L。 在基于多观测向量的稀疏表示问题中,L个稀疏信号有相同的稀疏结构。基于式(2),多观测向量的稀疏表示问题可表示为 ‖0,Λ={1,2,…,m}, s.t.AS=X (3) ‖1,Λ={1,2,…,m}, s.t.AS=X (4) 同样还有其他关于S的函数作为目标函数,如文献[12]所示,提出了基于凸优化问题的稀疏量测方法,表示为 (5) 式(5)中的混合范数‖·‖p,q定义为 ;q≥1 (6) 式中,S(i)表示矩阵S的第i行。MFOCUSS算法即要求解式(5)问题的最优解。 当二维稀疏信号的稀疏度比较低时,现有的多观测向量的稀疏重构算法,如MFOCUSS算法和MSBL算法,都有比较好的重构性能。然而,当稀疏矩阵的各向量有不同的稀疏结构,并且非零元个数较多时,上述方法将有可能在二维稀疏信号重构时失效。本文提出了一种基于多观测向量的序列降采样算法,来实现二维稀疏信号的重构。 基于压缩感知理论,重写式(2)为 X=ΨS (7) 式中,Ψ∈Rm×n表示测量矩阵,通常,m 二维信号的重构可通过序列降采样和序列观测来实现。假设E∈Rn×n为单位阵,降采样率为T并且ns=n/T。构造降采样矩阵Pt∈Rn×n(t=1,2,…,T)。矩阵Pt的第T×r+t(0≤r≤ns-1)行与矩阵E对应行相同,而矩阵Pt其他行的元素都为零。因此,矩阵Pt可表示为 (8) 可以看出,矩阵Pt只有第T×r+t(0≤r≤ns-1)行的第T×r+t个位置存在非零元素“1”,降采样的过程即是将降采样矩阵与信号S相乘。第t次观测信号可表示为 Xt=Ψt(PtS)=ΨtSt (9) 式中,Ψt∈Rm×n;St∈Rn×L。假设St和S的稀疏度分别为kt和k,则kt≤k,通常情况下,kt 在下面的分析中,假设矩阵Ψt对于所有的v∈Rn和部分常数c>0,满足 P(|‖Ψtv‖2-‖v‖2|≥ε‖v‖2)≤2exp(-cnε2/2) (10) 矩阵S的支撑基定义为 (11) 式中,S(l)表示矩阵S的第l列。向量S(l)的支撑基定义为 supp(S(l))={j,Sjl≠0} (12) 假设信号S∈Rn×L满足supp(S)=Ω。ΨtΩ表示由Ω索引的矩阵Ψt的列构成的子矩阵,并且假设矩阵ΨtΩ是非奇异的,那么当满足式(13)时,S是唯一的最优解。 ∉Ω (13) (14) 假设 ∀l∉Ω (15) 通过式(9)重构St的概率为 (16) 为重构信号S,需要序列地重构信号St(t=1,2,…,T)。 (17) 式中 (18) 式中,d(St)表示St中非零行的个数;λ是平衡估计效果的权重。 当完成St(t=1,2,…,T)的重构后,二维稀疏信号就可以重构出来,如图1所示。 图1 序列降采样重构Fig.1 Sequential down-sampling recovery algorithm 根据上述分析,所提的多观测向量的序列降采样重构方法流程可表示如下: 步骤1构造降采样矩阵Pt(t=1,2,…,T),得到观测信号Xt; 步骤2利用MFOCUSS方法求解式(18)优化问题,重构信号St,其重构概率可用式(16)表示; 步骤3重复上述步骤,直至t=T,通过式(17)计算最终重构的稀疏矩阵信号。 本节通过对仿真产生的模拟信号的重构效果验证本文算法的有效性。假设二维稀疏信号S各向量所包含的非零元素的位置和元素值是不相关的。‖S(l)‖0=k,l=1,2,…,L。k个非零元的位置是随机确定的,非零元素的元素值服从标准高斯分布。假设n=100,L=5,m=50。在第1次仿真实验中,假设降采样率T=2。当k=10时,初始信号如图2所示。 图2 初始信号Fig.2 Initial signal 从图2可以看出,稀疏矩阵不同向量间非零元所在位置不同,不满足传统的多观测向量重构方法模型。 图3 不同算法的二维稀疏信号重构概率Fig.3 2D sparse signal recovery probability with difference approaches versus sparsity 从图3可以看出,利用本文提出的SDR-MFOCUSS算法可实现二维稀疏信号的精确高概率重构。 在第2个仿真实验中,同样假设降采样率为T=2,对比了SDR-MFOCUSS算法和SDR-MSBL算法的计算时间,如图4所示。 图4 SDR-MSBL和SDR-MFOCUSS算法的运算时间Fig.4 Comparison of CPU times for SDR-MSBL and SDR-MFOCUSS algorithms 从图3和图4可以看出,相比于MFOCUSS和MSBL算法,SDR-MFOCUSS算法和SDR-MSBL算法在稀疏矩阵重构方面有着更好的性能。但是,本文提出的SDR-MFOCUSS算法的计算量远小于SDR-MSBL算法,主要原因是SDR-MSBL算法的迭代过程计算量很大,因而有更高的计算复杂度。 图5对比了不同降采样率T的条件下,SDR-MFOCUSS算法和2D-SL0算法在稀疏矩阵重构中的重构概率。 图5 不同参数T时SDR-MFOCUSS算法重构概率Fig.5 Performance of SDR-MFOCUSS algorithm as a function of T 从图5中可以看出,当T=2时,SDR-MFOCUSS算法和2D-SL0算法有近似的重构概率,而随着降采样率T的增大,SDR-MFOCUSS算法相比于2D-SL0算法有更高的重构概率,证明了本文所提方法的优越性。 典型的飞机目标的逆合成孔径雷达图像通常满足本文描述的二维稀疏特性,本节通过对该类图像的重构来验证本文算法在自然图像重构中的有效性。 典型直升机目标的逆合成孔径雷达初始图像如图6所示,可以看出目标在整个图像域是二维稀疏的。 首先,统计车次信息。车次信息包含车次、出车方向、时间、股道约束、里程、是否为早/晚高峰等,如图2所示。 图6 初始雷达图像Fig.6 Initial radar image 对比不同方法对该类图像的重构效果,结果如图7所示。 图7 不同算法的图像重构效果Fig.7 Reconstructed images of different methods 参数算法SDR-MFOCUSSSDR-MSBLMFOCUSSMSBLMSE0.05130.04800.50460.4669时间/s0.13270.29790.69181.7274 从图7及表1可以看出,基于SDR-MFOCUSS算法和SDR-MSBL算法对图像的重构效果明显优于MFOCUSS算法及MSBL算法,而SDR-MFOCUSS比SDR-MSBL有更低的运算量和更短的运算时间,证明了本文方法在图像重构中的有效性和优越性。 本文引入了稀疏矩阵重构和多观测向量的稀疏表示问题。当稀疏矩阵的各向量有不同的稀疏结构时,传统的多观测向量稀疏重构算法,如MFOCUSS和MSBL算法,将会有较高的重构误差。本文构建了降采样矩阵,提出了一种新的序列降采样重构方法,结合MFOCUSS算法,可实现二维稀疏信号的精确重构。模拟信号及图像重构实验验证了本文方法在模拟信号及图像重构中的有效性和优越性。然而,当稀疏矩阵各向量间稀疏度相差很大时,所提方法重构误差将会急剧增大。后续工作将集中于该类矩阵,尤其是非零元只分布于某些列的矩阵的重构问题。 [1] BARANIUK R G. Compressive sensing[J]. IEEE Signal Process Magazine, 2007, 24(4): 118-121. [2] 王彩云,徐静. 改进的压缩感知测量矩阵优化方法[J]. 系统工程与电子技术,2015, 37(4): 752-756. WANG C Y, XU J. Improved optimization algorithm for measurement matrix in compressed sensing[J]. Systems Engineering and Electronics, 2015, 37(4): 752-756. [3] BERG E, FRIEDLANDER M P. Theoretical and empirical results for recovery from multiple measurements[J]. IEEE Trans.on Information Theory, 2010, 56(5): 310-316. [4] CHEN J, HUO X. Theoretical results on sparse representations of multiple - measurement vectors[J]. IEEE Trans.on Signal Processing, 2006, 54(12): 4634-4643. [5] WANG Y, FU T, GAO M, et al. Performance of orthogonal matching pursuit for multiple measurement vectors with noise[C]∥Proc.of the IEEE China Summit & International Conference on Signal and Information Processing, 2013: 67-71. [6] COTTER S F, RAO B D, ENGAN K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Trans.on Signal Processing, 2005, 53(7): 2477-2488. [7] WIPF D P, RAO B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Trans.on Signal Processing, 2007, 55(7): 3704-3716. [8] GHAFFARI A, BABAIE-ZADEH M, JUTTEN C. Sparse decomposition of two dimensional signals[C]∥Proc.of the 34th IEEE International Conference on Acoustics, Speech Signal Processing, 2009: 3157-3160. [9] 司菁菁,候肖兰,程银波. 基于块剪枝多路径匹配追踪的多信号联合重构[J]. 系统工程与电子技术,2016, 38(9): 1993-1999. SI J J, HOU X L, CHENG Y B. Joint multi-signal reconstruction based on block pruning multipath matching pursuit[J]. Systems Engineering and Electronics, 2016, 38(9): 1993-1999. [10] JIN Y, RAO B D. Support recovery of sparse signals in the presence of multiple measurement vectors[J]. IEEE Trans.on Information Theory, 2013, 59(5): 3139-3157. [11] ELDAR Y C, RAUHUT H. Average case analysis of multichannel sparse recovery using convex relaxation[J]. IEEE Trans.on Information Theory, 2010, 56(1): 505-519. [12] CHEN J, HUO X. Sparse representations for multiple measurement vectors (MMV) in an over-complete dictionary[C]∥Proc.of the 30th IEEE International Conference on Acoustics, Speech Signal Processing, 2005: 257-260. [13] RAUHUT H, SCHNASS K, VANDERGHEYNST P. Compressed sensing and redundant dictionaries[J]. IEEE Trans.on Information Theory, 2008, 54(5): 2210-2219.1 多观测向量模型
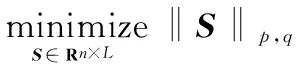
2 多观测向量的序列降采样重构
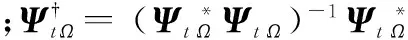

3 仿真实验及分析
3.1 模拟信号重构




3.2 图像重构

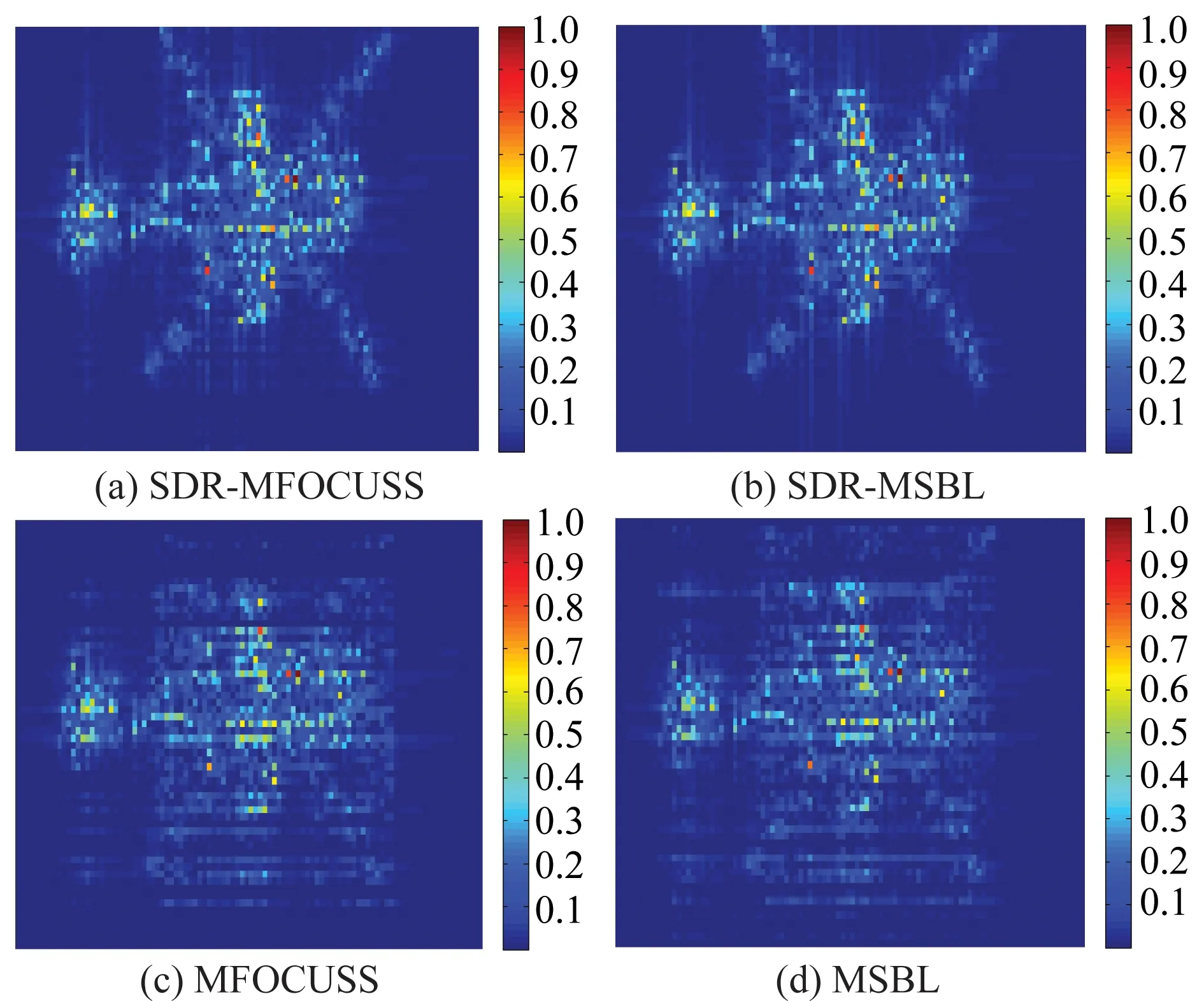
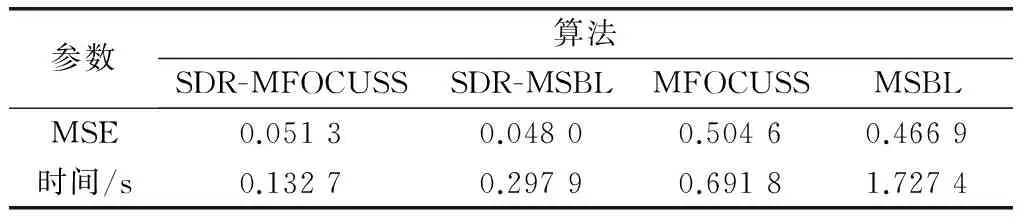
4 结束语

