巴特沃思型低通滤波器的归一化设计∗
汪宇 查明 李纵 王衡 刘庆
(中船重工集团公司第七二二研究所 武汉 430079)
1 引言
近年来,随着电力电子技术的高速发展,电路拓扑的形式也日益更新,其中,由多个“H桥”矩形波叠加而成的阶梯波形式输出功率放大器越来越广泛地应用于各种类型的固态大功率发射机[1~2]。虽然这种电路拓扑较好地抑制了功放输出端的高次谐波,但是在实际工程应用过程中仅仅通过这种技术手段还是难以达到相关标准的对大功率发射机输出谐波指标的要求,所以,仍然需要在功放输出端和天线调谐回路之间插入具有谐波抑制功能的环节[5]。本文主要介绍了巴特沃思型低通滤波器在阶梯波功放后级谐波抑制中的应用,并阐述了巴特沃思低通滤波器原理及特点,采用归一化方法,通过Matlab仿真软件进行频率特性仿真,最后给出了应用举例。
2 巴特沃思滤波器原理及特点
巴特沃思滤波器频率特性公式可由如下幅度平方函数定义[6]:
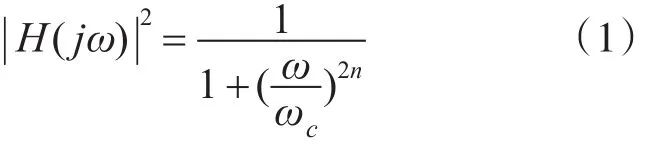
其中:n=滤波器的阶数,ωc=滤波器截止频率,即振幅衰减-3dB时的频率。该滤波器具有如下特殊性质:
1)对于所有n,当 ω =0时 ||H(jω)2=1为极大值,曲线具有最大平坦特性;
2) ||H(jω)2是ω的单调递减函数,不会出现幅度上的起伏;
3)n趋于无穷时,巴特沃思滤波器趋于理想低通滤波器。
根据式(1),推算出巴特沃思滤波器的衰减量公式如下
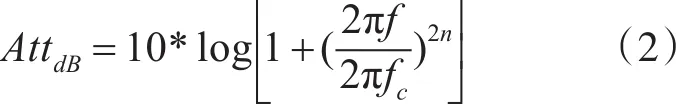
其中,fc是滤波器的截止频率,n是滤波器阶数,f是频率变量。也就是说,当 fc和n确定之后,上式计算的结果就是滤波器对频率的信号的衰减量。
取截止频率 fc=300Hz,频率范围为0~600Hz,利用Matlab软件仿真结果如图1所示。从图中可以看出,随着阶数的增加,滤波器通频带内越来越平坦,而阻频带内衰减特性越来越陡峭。由此可见,滤波器对信号的高次谐波分量能有效抑制。
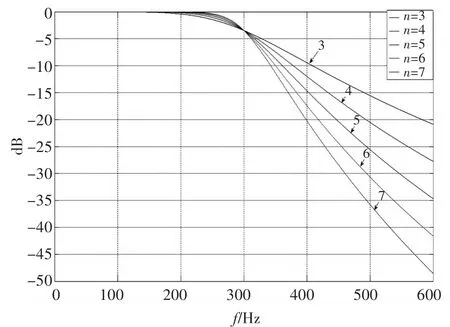
图1 3~7阶巴特沃思低通滤波器衰减特性
3 元件值的归一化计算
在实际工程应用的设计过程中,电路的电阻、电容和电感等元件的数值分布范围较大,计算时所处理的数据量大小相差甚远,容易产生计算误差。为便于理论分析和计算,需要将电路参数作归一化处理,根据处理结果建立通用的计算公式和图表[7~8]。
由于巴特沃思滤波器是一种全极点滤波器,其传递函数可表示为如下表达式:
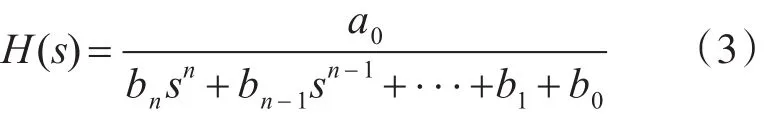
令 a0=k b0,bn=1,则有:
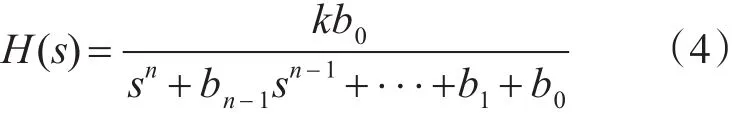
对于式(4),若n=2,4,6······传递函数可以分解为如下形式:
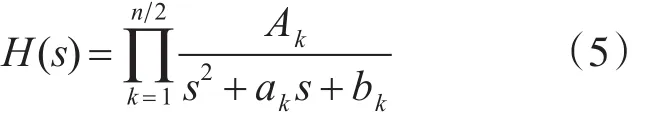
若n=3,5,7······则传递函数可分解为
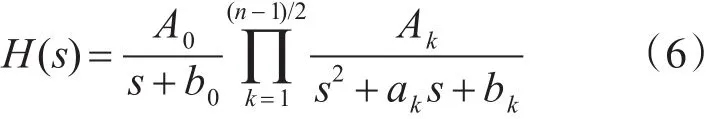
令 b0=1,k=1,2,···则各项系数可表示如下:
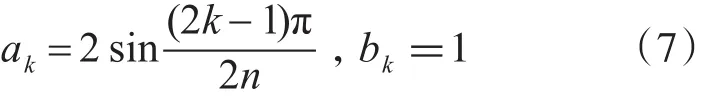
上式即为归一化截止频率为1/(2π)Hz,且特征阻抗为1Ω元件参数值的计算公式。
根据式(7),可建立不同阶数的元件值归一化参数表,如表1所示。应当注意的是,当阶数n为奇数时,滤波器的主电路结构有T型和π型两种形式。
得到归一化元件值参数后,可根据待设计滤波器特征阻抗和截止频率去归一化处理,得到实际所需要的滤波器元件值参数。

表1 n≤7归一化元件值参数表
截止频率比值[9]:

特征阻抗比值:

去归一化计算过程如下:首先将基准滤波器所有元件值除以M,从而把滤波器的截止频率从1/2πHz变换成待设计滤波器截止频率;接着将频率变换后的电路所有电感元件乘以K,所有电容元件除以K,即得到最终所设计的滤波器参数[10]。
4 传递函数归一化求解
在阶数不高的情况下,求出滤波器的阶和3dB截止频率后,直接利用查表法(表2)得到巴特沃思滤波器频率归一化模拟低通滤波器的传递函数,再通过频率变换的方法求得滤波器实际传递函数,这样可以省去计算极点的繁琐过程。
频率归一化(fc=1/2πHz)的低通巴特沃思滤波器的传递函数表示为

接着,用s/Ω代替式(8)中的s,就可得到截止频率为Ωc(Ωc=2πfc)的n阶巴特沃思低通滤波器的传递函数,表示如下:

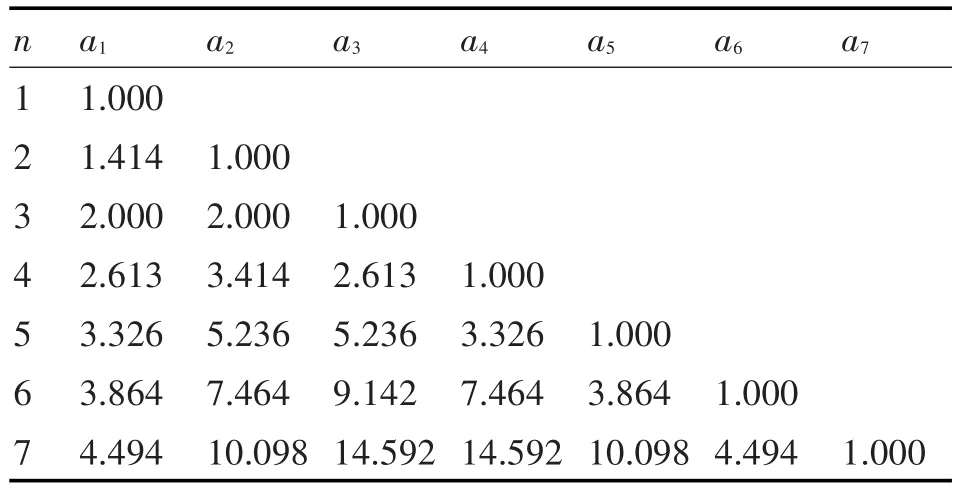
表2 n≤7归一化传递函数系数表
5 应用举例
某工程项目中应用的固态大功率发射机功率放大器需设计截止频率为180Hz、特征阻抗为15Ω的5阶T型巴特沃思低通滤波器,即3个电感和2个电容器。
设计步骤如下:

表3 巴特沃思低通滤波器(n=5)归一化元件值
第一步:查表1,得出归一化元件的参数。
第二步,去归一化。
根据式(8)计算截止频率比值:
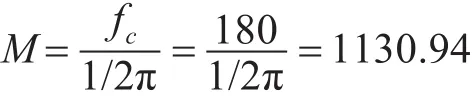
根据式(9)计算特征阻抗比值:

经过阻抗变换后去归一化元件值如表4所示。
高中物理中,强化“合作学习”教学理念,是在课程进行支出,对基本知识和定理定律进行大致了解的过程,也是掌握课程基础的体现.小组合作学习以小组为单位,在实际的教学良性循环中,实现高中生对物理知识点如匀变速直线运动中的平均速度V平=S/t (定义式) 下的有用推论和中间时刻速度 Vt/2=V平=(Vt+V0)/2 、末速Vt=V0+at等知识厚度的理解.

表4 巴特沃思低通滤波器(n=5)去归一化元件值
T型网络主电路拓扑结构如图2所示。

图2 T型巴特沃思低通滤波器(n=5)拓扑
第三步,求传递函数。
通过查表2可得归一化传递函数的系数如表5所示。

表5 巴特沃思低通滤波器(n=5)归一化传递函数系数
根据式(11)可得传递函数:

第四步:计算机模拟仿真。
根据所求解的滤波器传递函数表达式,利用Matlab仿真软件进行模拟仿真结果如图3所示。
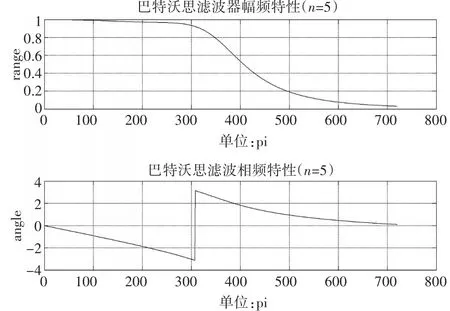
图3 T型巴特沃思低通滤波器幅频/相频特性
根据Matlab仿真结果可知,巴特沃思低通滤波器截止角频率为360π,对应fc为180Hz,通带内衰减平坦,无明显起伏,通带衰减小于-3dB,二倍频衰减小于-20 dB,满足工程应用设计要求。
6 结语
使用归一化计算方法可以使巴特沃思低通滤波器的设计更加简单、快捷、直观,根据滤波器传递函数进行Matlab仿真可有效验证计算结果的正确性,但在实际工程应用过程中还应考虑元件参数误差对滤波效果的影响,必要时应对计算结果予以修正。
[1]付微,查明,刘庆.一种新型固态大功率发射机的功放电路设计[J].软件导刊,2011,18(8):65-66.
[2]李腾,徐池,王永斌等.阶梯波合成开关功率放大器的研究与实现[J].舰船电子对抗,2013,39(2):86.
[3]陈道炼.DC-AC逆变技术及其应用[M].北京:机械工业出版社,2003,1(2):26-27.
[4]薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2011,4(3):156-158.
[5]姚天任.数字信号处理[M].北京:清华大学出版社,2011,5(10):419-421.
[6]曾盛,冯垛生.高次谐波及其抑制措施[J].现代电子技术,2002,24(90):40-41.
[7]森荣二著,薛培鼎译.LC滤波器设计与制作[M].北京:科学出版社,2005,3(1):49-52.
[8]陈思.巴特沃思滤波器的简化快速设计[J].信阳师范学院学报,1997(7):64-67.
[9]孟凡刚,骆霁嵘,高蕾等.基于直流侧有源谐波抑制方法的高功率密度多脉波整流器[J].电工技术学报,2017,6(2):34-36.
[10]王小军,施科研,董德智等.UPS逆变器谐波抑制环的分析与设计[J].电源学报,2017,5(3):45-46.
[11]王喜莲,王顺,程迪.考虑谐波电流的并网逆变器阻抗模型研究[J].北京交通大学学报,2017,34(60):36-37.
[12]Choose Wisely ,Carl Blake and Chris Bull.IGBTor MOS⁃FET[J].International Rectifier,2005,19(2):265-267.
[13]Cameron R J Advanced coupling matrix synthesis tech⁃niques for microwave filters[J].IEEE Trans Microwave Theory and Tech,2003,35(6):68-69.

