薄膜工艺制造误差对电路性能的影响
贾世旺,梁广华,刘巍巍 ,邢伯仑
(1.中国电子科技集团公司第五十四研究所,河北 石家庄050081;2.河北诺亚人力资源开发有限公司,河北 石家庄050035)
0 引言
薄膜基板制造是非常复杂的电子工艺加工过程,包含多个工序,涉及数十台设备。为了保证电路的微波性能,必须严格控制加工过程中的误差,当产品制造误差达到一定程度,电路性能可能会恶化,尤其是在微波和毫米波等较高频段。
为了量化制造误差对产品电性能的影响,需要开展薄膜工艺制造误差的研究。文献[1-4]论述了在机械多工序加工过程中误差传递及建模等问题。通过建立模型表征尺寸误差与各种误差源的逻辑关系,提出了工序制造过程中误差自修正能力评价指标;给出了误差不是各工序间误差简单累加的结论,除了考虑各工序的制造误差以外,还要考虑各工序间误差相互的影响,后道工序可能增加或者减少前道工序的加工误差。
文献[5]提出了基于SPC的装配过程质量控制方法。以期通过SPC方法应用,解决完成后检验的弊端,实现过程中监控并及时解决问题。同时,通过监测制造过程的数据变化,对质量特征变化进行评估和预测。
本文借鉴了研究机械多工序加工误差传递的思路和方法,对薄膜微波基板制造过程进行数据监控和统计分析,同时将分析结果带入到模型中进行电路仿真计算,量化了工艺误差对电路性能的影响。
1 薄膜工艺
薄膜工艺除了具有高精度、工艺稳定和设计灵活之外,可重复性高也是其重要特点[6-7]。薄膜通常是在真空条件下采用溅射的方法进行沉积,通过匀胶、曝光和显影等光刻操作将掩膜版上电路图形转移至基板上,然后经过电镀、去胶和刻蚀等工艺步骤完成图形的制作。与电路性能相关的薄膜工艺要求主要是线条精度,包括线宽、线间距及线条金属层厚度等测量指标。典型薄膜滤波器电路制造过程如图1所示。

图1 典型薄膜滤波器电路制造过程
2 工艺过程误差分析
一个稳定的工艺过程应该提供基本稳定的误差分布,电路设计人员可根据工艺线制造能力进行设计优化补偿,以提高设计的准确性。若某误差满足以下3个特征,则说明该误差分布是正态分布[8]。
① 一定测量条件下(人、机、料、法、环相对稳定),随机误差的绝对值不会超出一定边界;
② 小误差出现的几率大于大误差的几率;
③ 随着测量次数增多,绝对值相等、符号相反的误差出现的机会相等。
工序的正态分布情况,主要通过算术平均值和标准差2个数字特征来表征。通过这2个指标来衡量该工序的误差分布中心和误差分散性[9],2个指标的计算公式分别为:
(1)
(2)
δi=xi-x0,
(3)

为了检验薄膜工艺各工序的误差分布情况,可在数据汇总的基础上生成正态概率图并进行假设检验,以检查观测值是否服从正态分布。
从图1可知,薄膜工艺过程复杂,从掩膜制造到产品成型至少经过十几道工序[10-11],每道工序或多或少对最后的产品误差都有贡献。根据经验,清洗、打孔、去胶和外形切割等部分工序操作与线条无关,对最终线条精度基本无影响。因此,在数据分析时仅关注对产品质量影响较大的主要工序。
2.1 各主要工序误差
薄膜工艺中的掩膜、光刻、电镀及刻蚀是影响线宽精度的主要工序,电镀和刻蚀是决定线条金属层厚度的主要工序。
某批次薄膜产品采用常规加工工艺,电路性能要求线宽误差小于±5μm。该产品各主要工序实测线宽部分误差数据汇总如表1所示。

表1 各主要工序线条宽度部分误差数据 (μm)
其中,x1i代表第1道关键工序的第i个样本的误差数据,yi代表第i个样本的终检误差数据。各工序线宽误差数据是指该工序实测数据与CAM处理后的线条尺寸的差值。
2.1.1 掩膜
掩膜是将CAM处理完成的几何图形通过一定方法转移到特殊基板上加工而成,可供光刻工艺重复曝光使用。掩膜精度是保证产品精度的重要前提,目前主要掩膜种类包括铬版、干版和凸版等,其中薄膜工艺常用的是铬版,根据目前主要产品的精度要求,其误差应小于±1.0 μm。

2.1.2 光刻
光刻工序是整个薄膜工艺中相对复杂的工序,包括匀胶、前烘、曝光、中烘、显影和后烘等操作[12-13]。光刻误差包括工序设备本身、人员操作等引入的误差以及掩膜母版误差。曝光是利用波长为365~405nm近紫外线曝光机,将掩膜版上图形投影到涂覆有光刻胶的薄膜基板上,实现光刻胶的化学反应,完成图形转移。显影是将图形或非图形区域不需要的光刻胶溶解,显露出所需图形[14-15]。
对表1中光刻后线宽误差进行分析,数据服从正态分布,均值为0.40,标准差为0.842,光刻尺寸偏差在-1.351~+2.151μm范围内的置信概率为96%,误差数据分布如图2所示。

图2 各主要工序误差数据分布
与掩膜工序相比,光刻工序引入误差要大于上一道工序,且离散性增加,主要原因是一方面工艺线上德国SUSS曝光机的分辨率为1.0μm,设备能力限制;另一方面工序中采用人工手动对位曝光,操作人员技能水平影响不可忽略。因此在此工序中增加其他监测手段和加强人员技能培训是非常必要的。例如,利用光强计定期测试曝光机光强,监控光强及均匀性,并及时调整相关工艺参数;定期监控人员操作能力等。
2.1.3 电镀
电镀工序线条宽度误差数据服从正态分布,其均值为0.54,标准差为0.654,电镀尺寸的偏差在-0.81~+1.90μm范围内的置信概率为96%,误差数据分布如图2所示。
2.1.4 刻蚀
刻蚀是指通过特殊溶液、反应离子或机械等方式来剥离、去除不需要的材料。薄膜产品加工中常用湿法刻蚀。湿法刻蚀是纯粹的化学反应过程,多为各向同性刻蚀,存在侧腐蚀现象,对操作人员要求较高,该产品刻蚀后要求误差小于±4.5μm。
刻蚀工序线条误差服从正态分布,均值为0.05,标准差为1.07。刻蚀尺寸误差在-2.18~+2.28μm范围内的置信概率为96%,误差分布如图2所示。
2.1.5 终检
产品终检线宽误差服从正态分布,数据均值为1.613,标准差为1.311。在-1.11~+4.34μm误差范围内置信概率为96%,误差分布如图2所示。该产品误差范围满足工艺线±4.5μm控制要求。
2.2 多工序误差分析
薄膜工艺中各工序的制造误差均服从正态分布,根据各工序数据,分别对线宽和线条金属层厚度的最终尺寸误差进行回归分析。
多工序制造中,薄膜产品的最终加工误差是各工序误差的累计和传递的结果。应用统计分析技术对已获得的实测误差数据进行回归处理。
回归是对统计数据进行处理,并确定因变量与自变量的相关关系,建立相关性较好的回归方程(函数表达式),利用回归方程预测因变量的变化[16]。常用的回归分析方法有广义回归法、正交回归法、偏最小二乘回归法和非线性回归等[17]。
根据各种回归方法的特点及适用场合,选取广义回归法进行多元线性回归分析,确定式(4)线性回归模型中的回归系数[18]。
y=β0+β1x1+β2x2+…+βpxp+ε,
(4)
式中,y为因变量;自变量为{x1,…,xp};{β0,…,βp}为回归系数;ε为回归误差。
设检验工序线宽误差为因变量y,其他主要工序线宽误差{x1i,…,xpi}为自变量。应用统计分析工具对表1中的数据进行线条金属层宽度广义回归分析,S、R2和调整的R2是模型对数据的拟合优度的度量。S表示数据值偏离回归线的标准距离。对于给定研究,等式预测响应的效果越好,S越小;R2描述在观测的响应值中由预测变量解释的变异量的比例;调整的R2表示已根据模型中的项数调整的修正R2;PRESS是预测误差的平方和,一般而言,PRESS值越小,模型的预测能力就越好;R2(预测的)表示模型对新观测值预测响应的好坏程度。较大的预测的R2值说明模型的预测能力较强。
2.2.1 线宽
经分析计算得出线宽误差的回归方程:
y= 1.293-0.268x1i+0.835x2i-
0.114x3i+0.659x4i。
(5)
S大小为0.178,R2为98.42%,R2(调整)为 98.09%,预测误差的平方和PRESS为1.62,R2(预测)为96.75%。从以上预测模型评价指标可以看出,该回归方程可信度较高,能够反映表1中的统计数据情况。
从上式回归系数可以看出,光刻、刻蚀工序与最后的终检线宽误差正相关,降低工序误差能够提高最终产品的精度、掩膜、电镀工序与产品误差负相关。回归系数的大小代表了各工序对最终产品误差的贡献大小,各工序中光刻、刻蚀工序的影响程度最大,是需要重点关注解决的工序。
2.2.2 线条金属层厚度
利用广义回归分析方法,对线条金属层厚度误差数据进行处理,得出回归方程:
y=0.009+0.693x3i+0.013x4i+0.294x5i。
(6)
从式(6)中可以看出,电镀和刻蚀工序对金属层厚度的影响最大,去胶工序的影响较小。电镀和湿法刻蚀工序大部分由人工操作,因此,相比其他工序误差控制难度较大。为了降低金属层厚度误差,必须控制好电镀工序的电镀电流和时间等参数,加强对电镀液、刻蚀液成分的监测[19]。
线条厚度均值为4.2,标准差为0.37。加工误差在+3.43~+4.97 μm范围内的置信概率为96%,满足线条厚度大于3.2 μm的标准要求。
2.3 多工艺制造误差改进
为了验证式(5)中终验工序线宽误差与前几道主要工序误差之间关系是否正确,随后选取另一种有较高精度控制要求的产品进行验证。
该产品线宽误差要求控制±2.0 μm以内,在工艺流程中增加刻蚀保护,保证刻蚀精度,同时对光刻误差严加控制。第二种产品的线宽部分误差数据如表2所示。
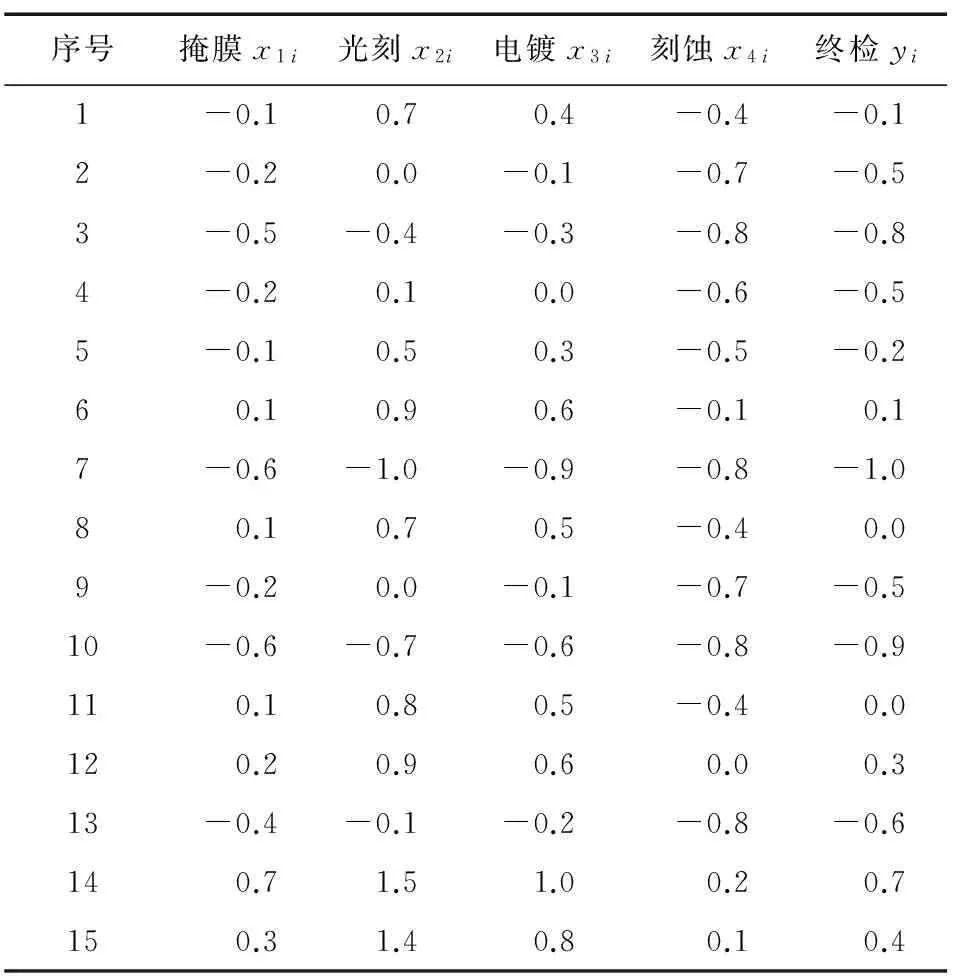
表2 各关键工序线条宽度部分误差数据 (μm)
再次对薄膜工艺线线宽数据进行误差回归分析,得出回归方程:
y= -0.259+0.513x1i+0.397x2i-
0.065x3i+0.211x4i。
(7)
从新的回归方程的系数可以看出,光刻、刻蚀工序对产品误差的影响程度与式(5)相比下降明显。
对第二种产品终检数据进行分析,数据服从正态分布。在置信概率为96%时,对于线宽误差范围缩小到-1.48~+1.02 μm以内。结果表明加强光刻、刻蚀两道工序控制,降低工序误差能够提高产品制造精度,两工序对产品误差影响的相关性降低,从而证明回归分析方法是有效的,得出的回归方程是可信的。
对于常规产品,经过大量实测数据分析、计算,得出该薄膜工艺线制造误差范围,在置信概率为96%时,线宽误差可控制在±4.5 μm以内,线条金属层厚度均值为4.2 μm,误差±20%以内;对于有更高精度线条要求的产品,可通过优化工艺流程,将线宽误差控制在±2.0 μm以内。设计师可依据这些数据对产品进行敏感性分析,从而在加工前预测产品性能。
3 多参数模型验证
为了分析薄膜加工过程中误差对电路性能的影响,以及多参数模型对仿真准确性的提升,以某Ka频段带通滤波器产品为例,进行电路仿真、加工测试和实验验证。该滤波器设计指标要求如表3所示。
实验验证思路:
① 采用理想模型进行三维电磁场仿真,即不考虑滤波器线条金属材料、厚度及加工误差等因素,默认材料为理想导体。分别进行滤波器设计和加工,产品用1#表示;
② 采用多参数电路模型,将线条宽带、厚度、材料、粗糙度及误差等该薄膜工艺线加工特性带入三维模型进行电磁场仿真,用2#表示;
③ 对1#、2#产品进行测试和数据对照分析。
表3中列出了部分两模型仿真及实测数据,明显可以得出以下结论:
① 1#理想模型仿真与1#实测值相比带宽收窄180 MHz,中心频率向高端偏移350 MHz左右,插入损耗实测值远大于计算值,抑制度不满足设计要求;
② 2#多参数模型仿真与2#实测值相比带宽收窄80 MHz,中心频率向高端偏移80 MHz左右,实测插入损耗略大于计算值;
③ 2#多参数模型的仿真结果与1#理想电路模型相比更接近实测值,特别是插入损耗更为接近,采用多参数模型进行电路设计准确性更高。
表3 滤波器设计要求及仿真、实测数据

产品中心频率/GHz3dB宽带/GHz插入损耗/dB幅频/1.0G/dB抑制@35G/dB回波损耗/dB设计要求28.604.50-3.002.0045.0-14.01#仿真28.605.05-0.181.7355.0-16.0实测28.954.87-1.201.8739.8-14.32#仿真28.605.06-0.951.6058.0-16.6实测28.684.98-1.300.9455.3-15.2
对2#仿真模型进行敏感性分析,设线宽为可变量。在线宽制造误差为±4.5 μm时,2#滤波器带宽收窄近100 MHz,中心频率向高端偏移160 MHz;在线宽制造误差为±2.0 μm时,2#滤波器中心频率向高端偏移达到90 MHz。线条金属层厚度大于3.2 μm以上,电性能基本无影响。
基于以上仿真分析,为了降低生产制造成本、提高生产效率,该款滤波器可以采用常规工艺控制线条精度,制造误差在±4.5 μm以内,电性能满足设计要求。在实际滤波器设计中,可通过适当加宽设计带宽,弥补工艺制造误差的影响。
4 结束语
应用概论数理统计原理对人员、设备相对稳定的薄膜工艺线各主要工序误差数据进行了分析,结果表明,各工序服从正态分布,现有加工能力满足产品电性能要求。对各主要工序与产品最终误差的关系进行了回归分析验证,证明回归方法及结论是可信的。
工艺误差统计分析方法可以推广到其他工艺线中,一方面可以通过数据监控工序的加工能力;另一方面可以通过回归分析,找出工艺线薄弱环节,采取措施,进一步提高工艺线制造能力。
最后,以某Ka频段滤波器进行了验证,采用多参数模型仿真,提高了滤波器设计准确性,仿真结果与实测数据更为接近;通过多参数模型敏感性分析,常规线条制造误差对该Ka频段滤波器性能的影响可以忽略。
[1] 杜世昌,王猛,奚立峰.多工序加工系统产品尺寸误差传递建模[J].机械工程学报,2011,47 (16):143-149.
[2] 蒋平,邢云燕,刘亚杰,等.多工序制造过程加工误差的传播分析和控制[J].数学的实践与认识,2013,43 (20):124-129.
[3] 沈颖华,杨建国.多工序加工过程的误差传递建模[J].机械工程师,2008(3):26-29.
[4] 孔德洋,王兆卫,刘健.多工序制造过程中的质量监控策略[J].哈尔滨工业大学学报,2012,44(3):87-91.
[5] 孙雪娇.基于SPC的装配过程质量监控系统研究[D].北京:北京交通大学,2015.
[6] 格普塔.厚薄膜混合微电子学手册[M].王瑞庭,朱征,译.北京:电子工业出版社,2005:143-150.
[7] 王育伟,刘小峰,陈婷婷,等.薄膜太阳电池的最新进展[J].半导体光电,2008(2):151-157.
[8] 梁晋文,陈林才,何贡著.误差理论与数据处理(修订版)[M].北京:中国计量出版社,2001.
[9] 马逢时,周暐,刘传冰.六西格玛管理统计指南-MINITAB使用指导(第2版)[M].北京:中国人民大学出版社,2013.
[10] 赵飞,王斌,党元兰.一种薄膜石英探针的设计与加工制造方法[J].无线电工程,2015,45(9):37-40.
[11] 陈凤翔,汪礼胜,祝霁洺.表面等离子体激元增强薄膜太阳电池研究进展[J].半导体光电,2011,32(2):158-164.
[12] Peter Van Zant.芯片制造-半导体工艺制程实用教程(第6版)[M]韩郑生,译.北京:电子工业出版社,2015.
[13] 张旻澍,谢安,李世玮.超声波检测在半导体工艺中的应用[J].半导体技术,2013,38(10):792-796.
[14] 党元兰,赵飞,梁广华,等.毫米波RF MEMS开关的研制[J].电子工艺技术,2016,37(1):35-39.
[15] 黄建.毫米波有源相控阵TR组件集成技术[J].电讯技术,2011,51(2):1-6.
[16] 王黎明,陈颖,杨楠.应用回归分析[M].上海:复旦大学出版社,2008.
[17] 田萍.纵向数据半参数回归模型的估计理论[M].郑州:郑州大学出版社,2008.
[18] 李志辉,李欣.MINITAB统计分析方法及应用(第2版)[M].北京:电子工业出版社,2017.
[19] 刘晓兰,朱政强,党元兰,等.基于体硅MEMS技术的悬浮微结构加工工艺研究[J].电子与封装,2015,15(7):37-40.

