基于变量节点更新改进的最小和算法
范 芳,冯雪林
(1.重庆邮电大学 通信与信息工程学院,重庆400065;2.中国科学院计算技术研究所 移动计算与新型终端北京市重点实验室,北京100190)
0 引言
LDPC码是一种纠错能力很强的线性分组码,在20世纪60年代由Gallager[1]博士提出。 20世纪80年代 Tanner推广了LDPC码并给出LDPC码的Tanner图表示[2],奠定了消息传递算法的基础。20世纪90年代Mackay等人[3]在Gallager的消息传递算法基础上提出了译码性能接近香农极限的BP算法,但其复杂度很大,不易于在硬件上实现。
为了满足在工程方面的应用,研究者们提出了一些简化的BP译码算法。其中,LLR-BP[4]译码算法是BP算法在对数域的简化算法。该算法没有损失BP算法的译码性能,但在迭代运算时仍需要大量的加法运算以及双曲正切函数的查表计算,复杂度较高,不易于应用实现。最小和算法[5]是一种目前应用最多的简化LLR-BP算法,用简单的比较和加法运算代替了原有复杂的指数和对数运算,很大程度上降低了计算复杂度,在硬件实现方面易于应用,但译码性能损失较多。为了弥补最小和算法带来的性能损失,在参考文献[6]中提出了一种归一化最小和算法,该算法是通过在最小和算法的校验节点更新基础上乘以一个补偿系数,利用线性归化的思想来修正幅度,提高译码性能。参考文献[7]中提出一种将最小和算法的变量节点与校验节点更新结果均乘以一个补偿系数的算法。参考文献[8]研究了一种自适应确定补偿系数的算法。
现有的简化算法,如最小和算法、归一化最小和算法以及其他改进的最小和算法都只是通过乘以补偿系数来提高译码性能的目的,没有考虑到可以通过与上一次变量节点信息结果的加权平均来提高译码可靠性,达到改善译码性能的目的。
本文在研究最小和算法的基础上,提出一种改进的最小和算法。该算法通过引入加权系数对前后2次变量节点外部信息值进行加权平均,修改了最小和算法的变量节点信息更新公式,保证了变量节点外部信息的可靠性,改善了译码性能。
1 已知的LDPC译码算法
LDPC码是一种由其校验矩阵H定义的具有特殊性的线性分组码[9]。特殊性体现在校验矩阵H中大部分都为0。在二元域上,LDPC码的校验矩阵H是由元素“0”和“1”构成的,假设有m行n列,则H中0的数量远远大于1的数量。LDPC码可以由校验节点和变量节点组成的Tanner图表示[10]。校验矩阵H的每一行为一个校验节点c,每一列为一个变量节点v。为了更好地说明二者之间的关系,假设

此时,m=6,n=6,对应的Tanner图如图1所示。

图1 校验矩阵的Tanner图
图中,c1表示矩阵H的第一个校验节点,也是矩阵H的第一行,与该校验节点相连的v3和v4变量节点,表示矩阵H的第3列和第4列。从矩阵H中可以看出,第1行第3列和第1行第4列刚好是该行非零元素1的位置,也就是说,在Tanner图中校验节点和变量节点的连线对应矩阵H中非零元素1的位置。
为了方便叙述,本文将与校验节点c相连的所有变量节点v的集合用M(v)表示,用N(c)表示与变量节点v相连的所有校验节点c的集合[11]。
LDPC一般采用基于软判决信息的迭代方法译码。在AWGN信道情况下,假设x=(x1,x2,…,xn-m)为随机产生的信息序列,LDPC编码后的信息序列为y=(y1,y2,…,yn),用BPSK方式调制后,经过信道加扰后,在接收端接收到的软判决序列为z=(z1,z2,…,zn)。由信道特性和接收到的软判决序列可以得到各变量节点的先验概率信息,通过变量节点和校验节点之间信息的传递更新,最终可以得到各变量节点的后验概率信息[12]。通过对变量节点的后验概率信息判决进行译码。下面介绍的几种常用译码算法都是基于对变量节点后验概率信息判决的译码算法。
1.1 LLR-BP译码算法
LDPC码经典的软判决译码算法是LLR-BP译码算法,它的译码效果与接近香农极限的BP算法一样,但有很高的复杂度,后面介绍的几种译码算法都是在LLR-BP算法的基础上进行简化和改进得到的[13]。
对于一个二元加性高斯信道,其信道输出服从高斯分布N(a,σ2)且输入信息序列服从先验等概,其中a是均值,σ2是方差。均值大小与调制方式有关,在二进制相移键控(BPSK)调制下,a为±1。对于一个接收随机变量zi,其中i=1,2,…,n,译码过程如下:
① 初始化
当信息序列经过高斯信道后,输出的先验似然比概率信息可表示为:

② 校验节点信息处理:校验节点传递给与其相连的变量节点的信息为


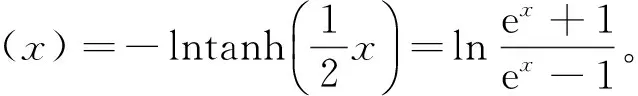
③ 变量节点信息处理:变量节点传递给与其相连的校验节点的信息为
④ 译码判决:根据收集的所有变量节点的后验概率信息进行译码判决,变量节点后验概率信息为

⑤ 停止译码
令k=k+1,重复以上步骤②~④,直到vHT=0或者达到规定的最大迭代次数时,译码停止,得到译码结果v。
从LLR-BP译码算法的校验节点信息处理公式可知,需要用到函数tanh,这个函数存在复杂的指数和对数运算,不适用于硬件实现方面,因此在此基础上进行了简化改进,提出了几种简化算法,虽然译码性能有损失,但大大降低了复杂度,适用于硬件实现方面[14]。
1.2 最小和算法
最小和算法只是在LLR-BP算法的步骤②进行了近似简化处理,得到如下改变后的校验节点信息处理公式:


其他步骤都与LLR-BP算法相同。
由简化公式可以看出,最小和算法没有了双曲正切函数的繁琐计算,用简单的比较和加法运算代替了原有复杂的指数和对数运算,很大程度上降低了运算量,在工程实现方面得到了大量应用[15]。
1.3 归一化最小和算法
归一化最小和算法是在最小和算法的校验节点更新处乘以一个系数∂,来弥补双曲正切函数的近似带来的译码性能损失[16]。归一化最小和算法只在最小和算法校验节点信息处理公式处做了变化,其余译码步骤均相同。归一化最小和算法的校验节点信息处理公式如下:


可知系数∂的选取影响归一化最小和算法的译码性能。系数∂的取值,要通过仿真来确定,通常选取合适的值为0.8~0.9[17]。归一化最小和算法弥补了最小和算法的一部分译码性能损失,但相比于LLR-BP算法,还存在性能损失。
2 基于变量节点更新改进的最小和算法
由现有的改进最小和算法可知,它们只是通过用补偿系数来修正校验节点外部信息的值,没有考虑到变量节点前后2次信息更新时存在的误差,这种误差会造成译码判决错误,译码可靠性降低[18]。根据最小和算法的译码特性,提出一种基于变量节点更新的改进最小和算法。该算法在计算变量节点更新时,通过引入加权系数β对最小和算法的变量节点的前后2次外部信息值进行加权平均,修正变量节点外部信息,改善译码性能。
改进算法的具体译码步骤如下:
① 初始化
② 校验节点信息处理


③ 变量节点信息处理
④ 译码判决

⑤ 停止译码
令k=k+1,重复以上步骤②~④,直到vHT=0或者达到规定的最大迭代次数时,译码停止,得到译码结果v。
由以上译码步骤可知,该算法保留了最小和算法在LLR-BP算法基础上,用简单的比较和加法运算代替原有双曲正切函数的繁琐计算,复杂度与最小和算法接近,并且通过对变量节点更新时进行前后两次外部信息值加权平均,保证译码的可靠性,与最小和算法相比,明显地提高了译码性能。
3 复杂度与误码性能分析
本文研究改进最小和算法时,采用加性高斯白噪声传输信道,BPSK调制方式,选用相同码型为QC-LDPC(1152,576)码,编码方法统一采用基于近似下三角校验矩阵的线性编码方法,设定最大译码迭代次数为30,对改进最小和算法的误码率性能进行仿真对比分析,验证改进最小和算法的有效性。
3.1 复杂度分析
基于变量节点更新改进的最小和算法在译码迭代时需要增加一个缓存器用来寄存上一次变量节点的外部信息。假设LDPC码的矩阵H为R行C列,对于行重和列重都固定的规则LDPC码,设行重为dc[19]。对比最小和算法,改进最小和算法只增加了一次加权求和运算,因此只增加了R×dc的运算量。对比LLR-BP算法,改进最小和算法增加的这部分运算量还是很少的,但是却可以很好修正变量节点外部信息,保证译码的可靠性,提高了纠错性能。
3.2 误码性能分析
不同β与最小和算法的误码性能对比如图2所示,通过仿真对比得出,当加权系数β为0.9时,改进最小和算法能获得较好的译码性能。

图2 不同β与最小和算法的误码性能对比
选取改进最小和算法的加权系数β为0.9,将改进最小和算法与LLR-BP算法、最小和算法、归一化最小和算法的误码率性能进行仿真对比,结果如图3所示。
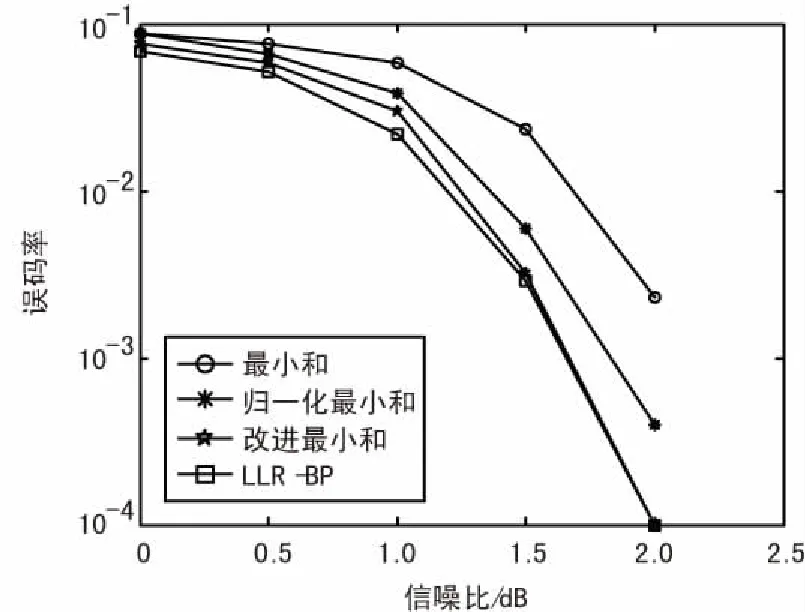
图3 改进算法与其他算法误码性能对比
由上面的仿真对比结果可知,在信噪比较低时,LLR-BP算法的性能最优,其次分别是改进最小和算法、归一化最小和算法、最小和算法。但随着信噪比的提高,改进最小和算法的误码率逐渐接近LLR-BP算法,当误码率为10-4时,相比最小和算法与归一化最小和算法性能提升分别约为0.5dB和0.2dB。
综上所述,改进最小和算法纠错性能优于已有的最小和算法和归一化最小和算法,并且随着信噪比的提高,其纠错性能接近LLR-BP算法,并且计算复杂度低于LLR-BP算法,是一种有效且具有发展前景的译码算法。
4 结束语
本文通过对比总结几种经典的LDPC译码算法,在最小和算法的基础上,对变量节点更新进行改进,提出一种改进的最小和算法。该算法的计算复杂度与最小和相比只增加了小部分,纠错性能得到了约0.5dB的提高,并且其复杂度低于传统的LLR-BP译码算法,随着信噪比的提高其性能接近LLR-BP算法,因此该算法在工程应用上具有很大的发展前景。
[1]GALLAGERG.Low-Density-Parity-CheckCodes[J].IRETransactionsonInformationTheory(S0096-1000),1962,8(1):21-28.
[2]TANNERRM.ARecursiveApproachtoLowComplexityCodes.IEEETransactionsonInformationTheory[J].1981,27(5):533-547.
[3]MACKAYDJC,NEALRM.NearShannonLimitPerformanceofLow-DensityParity-CheckCodes[J].ElectronicsLetters,1996,32(18):1645-1646.
[4]FOSSORIERMPC,MIHALJEVICM,IMAIH.ReducedComplexityIterativeDecodingFollowDensityParityCheckCodesBasedOnBeliefPropagation[J].IEEETransactiononCommunication,1999,47(5):673-680.
[5] 吴湛击,王文博.现代纠错编码与调制理论及应用[M].北京:人民邮电出版社,2008.
[6]HOCEVARD.AReducedComplexityDecoderArchitectureviaLayeredDecodingofLDPCCodes[C]∥IEEEWorkshoponSignalProcessingSystems(SIPS),IEEE,2004:107-112.
[7]ZHANGXM,TAIY.High-speedMulti-block-rowLayeredDecodingforQuasi-cyclicLDPCCodes[C]∥SignalandInformationProcessing(GlobalSIP),IEEE,2014:11-14.
[8]ZHANGT,KESHABKP.Joint(3:κ)-regularLDPCCodeandDecoder/EncoderDesign[J].IEEETransactionsonSignalProcessing,2004,52(4):1065-1079.
[9] 王新梅.纠错码与差错控制[M].北京:人民邮电出版社,1989.
[10] 庄梦溪.高速LDPC码编译码器的研究与实现[D].西安电子科技大学,2012.
[11]FANGYi,BIGuoan,GUANYongliang.DesignandAnalysisofRoot-protographLDPCCodesforNon-ergodicBlock-fadingChannels[J].IEEETransactionsonWirelessCommunications,2015,14(2):738-749.
[12] 王飞,罗益,王振华,等.LDPC码在BPSK通信系统中的性能分析[J].无线电通信技术,2015,41(1):13-16.
[13]Al-FUQAHAA,GUIZANIM,MOHAMMADIM,elat.InternetofThings:aSurveyonEnablingTechnologies,Protocols,andApplications[J].IEEECommunicationsSurveys&Tutorials,2015,17(4):2347-2376.
[14] 张福星,许生旺.一种改进的多元LDPC码译码算法[J].无线电通信技术,2016,42(6):56-58,69.
[15]ALBAYRAKC,TURKK.BP-basedApproximationMethodsforRatelessCodes[C]∥SignalProcessingandCommunication
ApplicationConference,Turkey,2016:1897-1900.
[16]KUMARAYVAC,WAVEGEDARACB.ImprovedLDPCDecodingAlgorithmsBasedonMin-SumAlgorithm[C]∥MoratuwaEngineeringResearchConference,2016:108-113.
[17]MOHSENINT,BAASBM.ASplit-DecodingMessagePassingAlgorithmforLowDensityParityCheckDecoders[J].JournalofSignalProcessingSystems,2010,61(3):329-345.
[18] 孙斌,王钢,杨文超,等.一种改进型LLRBP算法的LDPC译码研究[J].无线电工程,2015,45(3):4-6.
[19]MAHDIA,PALIOURASV.OntheEncodingComplexityofQuasi-cyclicLDPCCodes[J].IEEETransactionsonSignalProcessing,2015,63(22):6096-6108.

