卫星导航模拟器星座轨道外推方法研究
叶红军,潘 峰,李 笛
(1.卫星导航系统与装备技术国家重点实验室,河北 石家庄050081; 2.北京卫星导航中心,北京100094)
0 引言
卫星导航模拟器可以通过仿真的方式生成各种动态条件接收机天线端的导航信号,可以更加直观地认识轨道的空间分布、运行周期以及卫星系统在地面上的DOP值分布等,结合信号处理算法可以十分逼真地对北斗、GPS等导航系统的观测值信号进行仿真,生成模拟的载波和伪距观测值,实现对接收机的调试及测试[1-4]。逼真的模拟导航星座运行及空间信号的各种特征,是模拟器开展接收机测试的前提[5-7],其中长时间高精度的实现运行轨道的模拟是模拟器产生导航电文的基础,北斗导航系统由于我国国土的特点在星座设计上是一种多轨道面混合组网的方式,对其高精度的导航模拟轨道外推与GPS星座相比更加困难,同时在模拟器运行中还需要综合考虑工程的可实现性,针对此问题,开展针对北斗混合星座的长时间精密轨道递推研究,并实现精度与计算量的统筹,提高工程可实现性。
1 导航卫星轨道误差因素
导航卫星在空间轨道运行中将受到各种摄动力的影响,使得其运行轨道变得很复杂,以致初始时刻的位置和速度(或6个轨道参数)不再是理想的二体问题情况下的常数,而是时间的复杂函数。卫星受力一般分为两大类:中心力与非中心力[8-10]。保守摄动力包括地球非球体引力位摄动、N体摄动、因日月引力引起的地球固体潮摄动及海潮摄动、大气潮摄动、地球自转形变摄动以及因相对论效应引起的摄动等。非保守摄动力包括大气阻力摄动、太阳直射辐射压摄动和地球反照辐射压摄动等[11]。
1.1 重力场模型分析
卫星受地球非球形引力是否精确取决于地球重力场模型的精确程度。确定引力场模型的方法主要有3种:通过对卫星轨道的跟踪观测、利用陆地重力测定法和利用高度计数据确定引力场模型。
在近40多年的时间里,经过研究发现对于高度计数据误差影响最大的就是卫星轨道误差,对于轨道误差影响最大的就是地球重力场模型的精确程度,因此在重力场模型上投入了广泛的、深入的研究,从1959年第一次精密确定J2项系数以来,到目前先后有Kozai、Itzsak、Kaula、Rapp、Gaposchkin、GEM-9、GEM-10B、GRIM3-L1、GRIM4-2S2、GEM-T3、JGM-3、EGM96S。JGM-3对于精密定轨已经是一个非常精确的重力场模型,是70阶70次的模型[12]。尽管JGM3相对于精密定轨已经足够,人们又发展了新的重力场模型,利用了40颗卫星的跟踪数据,采用GPS和TDRSS卫星对卫星跟踪系统,使引力场模型又有了进一步的提高,获得了EGM96S(70×70)和EGM96(360×360)模型。
因此,可以通过选择JGM-3、EGM96S和EGM96模型来计算卫星轨道,能达到比较理想的轨道外推效果。
1.2 大气阻尼模型分析
大气阻尼模型目前难以建立十分精确的模型。迄今为止虽然已经建立了很多大气模型,但各模型之间的差异比较大,在200 km的高度上,各模型典型密度差为20%,在较高的高度上相差更高。目前大气模型有:Harris-Priester、Jacchia-71、Jacchia-Roberts、Jacchia-Lineberry、Jacchia-Gill、Jacchia-77、Jacchia-Lafontaine、MSIS-77、MSIS-86、TD-88和DTM[13]。
J71模型提出了一个合理的大气密度模型的描述,因此广泛的应用于精密定轨和轨道外推研究中。J71模型考虑了周日和27天太阳效应,根据大气密度是角度ψd(卫星和周日峰之间的角度)的函数,通过对卫星观测推导而来。在高度h大气密度被表示为:
(1)
式中,
logeρ′(h)=-16.021-1.985×10-3h+6.383e-0.026h;
F10.7为10.7cm太阳辐射流量;


(2)
除了J71模型的广泛使用外,各种其他密度模型也依然有其应用价值,其中也不乏简单的、容易执行的和精巧的理论的模型,为了比较这些模型,表1是以J71模型为基准计算的各模型平均大气密度、最大大气密度之差以及在CPU计算时间上的差异。

表1 各种大气密度模型与J71的比较CPU
2 高稳定轨道积分方法
在卫星的精密轨道外推中,积分器的设计是一项基础工作。它的作用体现在2个方面:如果建立了卫星的力模型,则可以获得卫星的运动方程。通过对卫星的运动方程进行积分就可以获得卫星的运动状态(位置和速度向量);同时积分器要完成变分方程的积分,获得卫星状态对轨道参数和力模型参数的偏导数用于轨道外推。程序运行的大量时间是在积分过程,因此除了动力学模型需要很精确外,外推计算中也需要高精度的积分器。
目前积分器所采用的比较成熟的算法有以下几种:① Runge-Kutta算法;② Adams算法;③Cowell算法。
2.1 Runge-Kutta算法
Runge-Kutta方法可以用来解如下的初值问题:
(3)
式中,X0为变量X的初值;F为变量t和X的函数。
如果步长为h,则Runge-Kutta算法可以用来计算变量X在t0+h的值X(t0+h)。重复这种步骤就可以获得一系列的解X(t0+h),X(t0+2h),X(t0+3h),……,X(t0+nh),其中,n是一个整数。则利用Taylor级数可以将X(tn+nh)在点tn处展开如下:
(4)
本质上,Runge-Kutta算法是对同阶的Taylor级数展开的逼近。将此算法向前推进一步就需要处多次计算函数F的值,在多数实际应用中,这是非常耗时间的。因此,称Runge-Kutta算法为单步算法,该方法一般用作多步法的起步算法。
积分的误差将取决于步长的大小和函数F的性质。为了保证轨道积分具有合理的精度,在计算中对积分步长进行自适应控制是一种可取的办法。由于轨道的周期性,因此,在轨道积分中仅仅需要对一些特殊的周期采用步长的控制。Press于1992年提出了一种新的控制方法,每次积分进行2次计算,一次是采用全步长进行,然后以半步长进行2次;将这2种方法获得的结果进行比较就可以判断是否需要对步长进行改变。
2.2 Adams算法
对初值问题,其解为:

(5)
Adams算法使用Newton向后差分计算来拟合函数F,表达式如下:

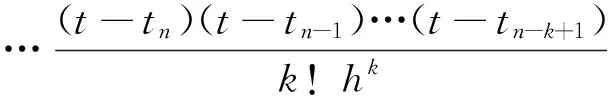
(6)
式中,Fn为函数在tn处的取值;h为步长;▽kF为函数F的n阶向后差分。
在多数情况下Adams-Moulton方法要比Adams-Bashforth方法的精度更高;但是,在计算函数值Fn+1前必须要有Xn+1,因此,在使用Adams-Moulton方法时要使用递归的方法。一种比较简单的方法是利用Adams-Bashforth方法计算Xn+1的近似值,然后利用Xn+1的近似值计算Fn+1的近似值。经验表明,上述方法一般可以达到足够高的精度。
2.3 Cowell算法
对初值问题
(7)
其解可以写为:
(8)
式中,X为卫星的位置向量。或者说,函数F只是问题的函数而与速度无关。
与Adams-Bashforth方法类似,函数F由式(9)拟合:

(9)
由于使用了Fn+1来拟合函数,因此,Cowell方法可以达到比Stormer方法更高的精度。同样,计算Fn+1需要Xn+1上的值,因此,解决此问题需要进行迭代。可以使用Stormer方法计算Xn+1的近似值,然后利用该近似值计算Fn+1从而开始迭代过程。
3 算法选择与流程设计
为了解决定轨问题中的初值问题,上面分析了3种积分方法。Runge-Kutta方法是一种单步算法,不同阶数的Runge-Kutta方法具有不同的计算公式。即使在同阶的Runge-Kutta方法中,其系数的确定也不是唯一的,在每次向前推进积分时,需要多次计算函数值,这在计算效率上是非常不利的。Runge-Kutta方法一个很重要的特点在于它是自起步的,因此,一般Runge-Kutta方法用作多步算法的起步算法。
Adams算法是一种多步算法。由于其系数间存在简单的对应关系,因此,如果需要提高该算法的阶数则很方便。但由于该算法是不能自起步的,在起步后,每次积分都只需要计算一次函数值,因此,特别对那些具有复杂关系的初值问题具有很高的计算效率。如果想达到更高的精度,可以通过在迭代过程中综合使用Adams-Bashforth和Adams-Moulton方法获得[14-16]。
Cowell方法也是一种多步算法,其阶数也可以很方便地提高,但该方法也需要其他方法提供起步值。研究表明,Cowell方法具有比同阶Adams方法更高的精度,但是,根据本文推导过程可以发现,该方法只适用于右函数仅仅是时间和卫星位置向量函数的特殊情况。但是,像空气阻力就与卫星的速度有关。因此,Cowell方法只能在部分问题中使用,其他综合了Cowell算法的方法也具有这种特点。
通过上面的讨论,很明显需要将卫星运动过程中受到的力进行分类:一类力只与时间和卫星的位置有关,其他的力为另一类。第1类可以使用Cowell方法进行积分,而第2类就可以采用Adams方法。2种方法的起步初始值均由Runge-Kutta方法提供。
至于如何选择积分步长和积分器的阶数则取决于轨道递推所需要的精度。一般,在软件设计中,这2个参数会设置成可调节的,这样,在几次迭代运行后就可以确定一个比较合适的值。在实用中,一般采用8阶Runge-Kutta方法和12阶Adams方法就足够了。但并不是步长越小越好,也不是阶数越高越好。
表2对几种常用在卫星轨道递推中的数值积分器特征进行了对比。根据积分器计算下一步点用到前面一个还是多个步点的信息,可把积分器分为单步法和多步法;根据积分过程中积分步长是固定不变还是自动调控,可把积分器分为固定步长法和变步长法;根据多步法积分过程中是否用到差分算子,可把多步法积分器分为求和型和非求和型(也叫一般型);根据积分器是对一阶还是二阶微分方程积分,可把积分器分为一次型和二次型。一般来说,多步法优于单步法,因为随着数值方法的阶数增加,后者计算右函数的次数将增加,而前者基本保持不变,对于轨道递推这样的动力学问题,方程右函数的计算是十分复杂,数值积分耗时主要表现在右函数的计算上。变步长法优于固定步长法,因为变步长法对椭圆型轨道更有效;求和型优于非求和型,因为求和型更能减少计算的省略误差。二次型优于一次型,因为在相同的精度要求下,对二阶微分方程求解所允许的步长比对一阶微分方程求解时使用的步长大的多。
每种积分器既有其优点,也有其缺点。在实际的应用实践过程中,要根据具体问题来选择适当的积分方法,既要考虑积分的精度、稳定性和收敛性,也要考虑计算的速度,同时还要考虑程序设计的复杂性。
表2 数值积分方法特征

数值积分方法单步法/多步法变步长/固定步长求和型/非求和型一次型/二次型RK(Runge-Kutta)方法单步法固定步长NA一次型RKF(Runge-Kutta-Fehlberg)方法单步法变步长NA一次型Adams方法多步法固定步长非求和型一次型Cowell方法多步法固定步长非求和型二次型
由于北斗卫星星座为由GEO、IGSO和MEO卫星组成的混合星座,因此在实际导航模拟器轨道外推算法上采用RKF和Adams相结合的方法来进行实现。轨道积分器主要完成对GPS/BDS/GLONASS/GALILEO卫星的轨道积分外推工作。数据仿真技术流程图如图1所示。

图1 卫星导航模拟器轨道积分器流程
该模块输入的是卫星的初始历元以及力模型的基本参数,结果为积分得到的参考轨道以及相应的对各动力参数的偏导数。该积分器起步算法采用的是Runge-Kutta-fehlberg方法(RKF),它是一种嵌套的Runge-Kutta方法,容易在计算机上实现,而且变步长方便,能保证所需要的精度,稳定度也较好。起步后,采用基于Adams显式Adams-Bashfort公式和隐式Adams-Moulton公式,以及Cowell公式的预报校正多步线性积分算法进行数值积分。以上算法非常成熟,而且基本上都可以满足精度要求。但是,由于低轨卫星受力状况比较复杂,某些动力模型参数需要分段估计,因此需要积分器能处理力模型参数突变的能力。
4 仿真结果及分析
卫星导航模拟器轨道仿真模块与STK10.0的高精度轨道预报模块(HPOP)积分设置如表3所示,力学模型设置如表4所示,采用相同的地球定向参数文件。考虑的力学模型有地球引力、地球固体潮汐影响、日月引力、太阳辐射压力与相对论效应影响,其余影响较小的力学模型未考虑在内。
导航星座轨道仿真位置差异如表5所示。北斗卫星星座轨道仿真三维位置差异均方根如图2所示。
表3 导航星座轨道仿真积分方法设置

积分设置项现有轨道仿真STK高精度轨道预报积分开始时刻UTC时间2010年1月1日0时0分0秒积分初始值地心固定坐标系积分坐标系地心惯性坐标系积分方法RKF6(7)启动Adams11阶预估校正RKF7(8)积分步长固定60s相对误差控制最小步长1s最大步长86400s输出步长60s积分时长24h,86400s输出坐标系地心固定坐标系
表4 导航星座轨道仿真力学模型设置
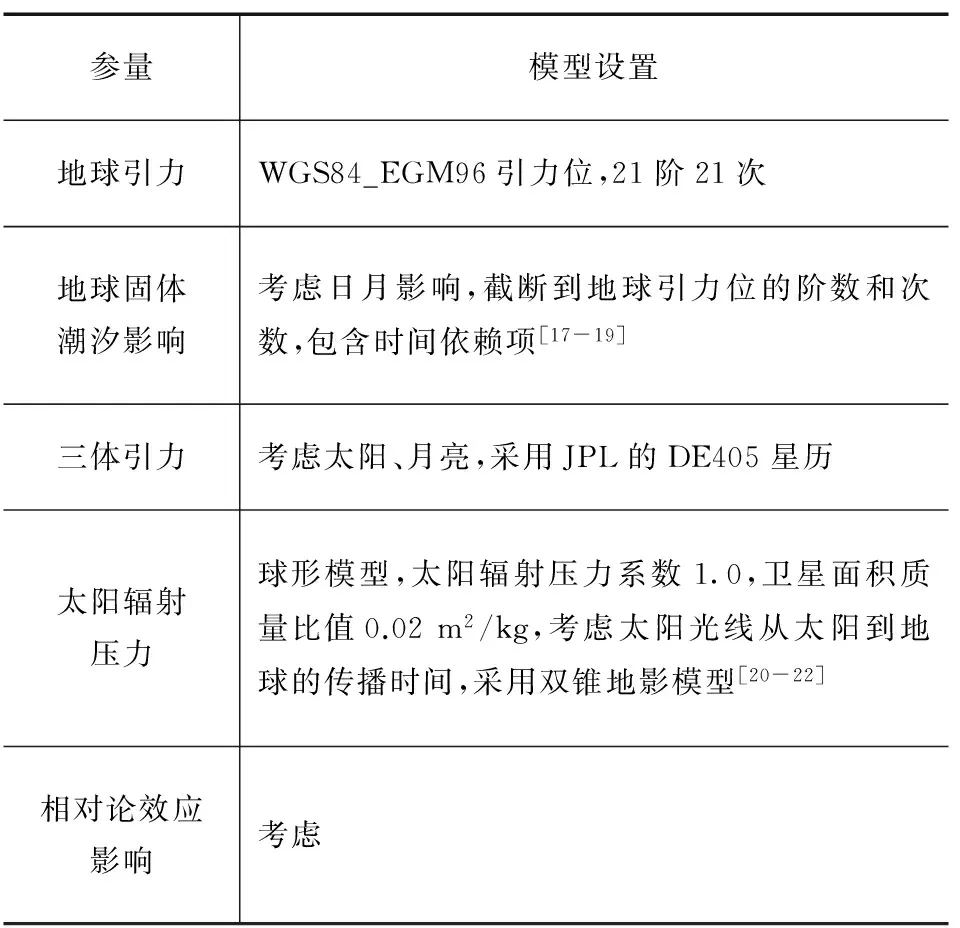
参量模型设置地球引力WGS84_EGM96引力位,21阶21次地球固体潮汐影响考虑日月影响,截断到地球引力位的阶数和次数,包含时间依赖项[17-19]三体引力考虑太阳、月亮,采用JPL的DE405星历太阳辐射压力球形模型,太阳辐射压力系数1.0,卫星面积质量比值0.02m2/kg,考虑太阳光线从太阳到地球的传播时间,采用双锥地影模型[20-22]相对论效应影响考虑
表5 导航星座轨道仿真位置差异均方根

导航星座位置差异均方根/m限差/mCOMPASS0.013GPS0.018GLONASS0.026Galileo0.0170.1
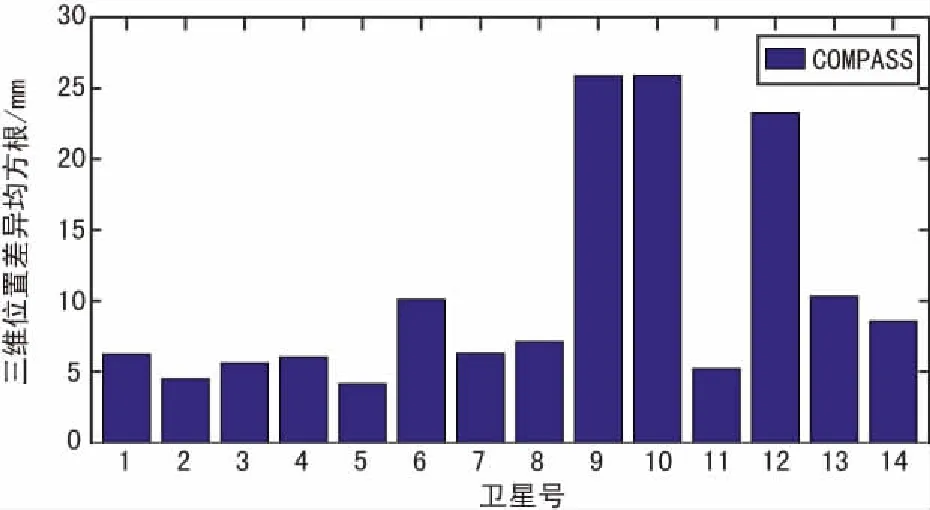
图2 北斗卫星星座轨道仿真三维位置差异均方根
通过图2可以看出在相同参数设置下,通过该方法仿真的结果与STK软件轨道数据偏差远小于0.1m,可以满足卫星导航模拟器数学仿真软件的要求并基于此产生相应的导航星历和电文。
5 结束语
通过调研分析国外已有成熟的精密定轨及轨道外推技术,结合卫星导航模拟器工程化实现需求,深入研究了卫星导航星座轨道外推仿真的数学模型和算法,完成了各种主要误差因素对轨道仿真精度的影响分析,确定了卫星导航星座轨道外推的方法和软件方案,完成了导航系统星轨道仿真软件流程设计与实现,仿真成果与STK软件轨道数据偏差小于0.1m,达到了较高的精度,输出结果包括卫星轨道坐标(根数)、卫星运动速度,可实现48h的轨道外推,解决了以往轨道外推随着时间逐渐偏差加大的问题,对生成连续的卫星导航星历支持卫星导航接收机开展长时间测试验证具有直接的支持作用。
[1] 冉承其.“北斗”卫星导航系统建设与发展[J].国际太空,2013(10):11-15.
[2] 谭述森.卫星导航定位工程(第2版)[M].北京:国防工业出版社,2010.
[3] 李隽.卫星导航信号模拟器体系结构分析[J].无线电工程,2006,36(8):30-39.
[4] 叶红军.多模式卫星导航模拟器设计与实现[J].无线电工程,2014,44(7):43-46.
[5] 黄勇,胡小工,王小亚,等.中高轨卫星广播星历精度分析[J].天文学进展,2006,24(1):81-87.
[6] 高玉东,郗晓宁,王威.导航卫星广播星历拟合改进算法设计[J].国防科技大学学报,2007,29(5):18-21.
[7] 楼益栋,刘万科,张小红.GPS卫星星历精度分析[J].测绘信息与工程,2003,28(6):4-6.
[8] 赵娜,董峥.卫星星座运行管理方法研究[J].无线电工程,2010,40(6):62-64.
[9] 刘季.北斗GEO卫星轨道算法研究[J].测绘地理信息,2012,37(5):33-36.
[10] 吴静,常青,吴今培,等.高动态GPS信号模拟器卫星星历产生方法研究[J].无线电工程,2004,34(5):42-60.
[11] 刘子令,姚志成.卫星/惯性组合导航信号仿真器设计
[J].无线电工程,2014,44(7):39-50.
[12] 郁聪冲,边少锋.现阶段北斗卫星导航系统可用性分析[J].海洋测绘.2012,32(5):74-76.
[13] 高为广,苏牡丹,李军正,等.北斗卫星导航系统试运行服务性能评估[J].武汉大学学报信息科学版,2012,37(11):352-355.
[14] 雷浩,廉保旺,何伟,等.STK北斗二代卫星导航系统在亚太地区DOP值仿真分析[J].火力与指挥控制,2014,39(6):52-55.
[15] 周兵.北斗卫星导航系统发展现状与建设构想[J].无线电工程,2016,46(4):1-4.
[16]WANGMengli,SUNGuangfu,WANGFeixue,etal.WeightedGeometricDilutionofPrecision’sAnalysisforMixedConstellationNavigationSystem[J].ChineseSpaceScienceandTechnology,2007,10(5):50-56.
[17]CAIHongliang,LIXing.WeaknessAnalysisofNavigationConstellationBasedonServiceVailability[J].CSNC2015,2015162(3):150-156.
[18] 高孝杰,张晶晶,高微,等.基于网络模式的北斗高精度定位数据播发[J].计算机工程,2017,43(10):1-4.
[19] 李飞琦,鲍泓,潘峰,等.智能车导航中的路口轨迹生成策略[J].计算机工程,2017,43(8):1-7.
[20] 黄建生,王晓玲,王敬艳,等.GPS导航定位设备测试技术研究[J].电子技术与软件工程,2013(6):36-37.
[21] 罗大成,刘岩,刘延飞,等.星间链路技术的研究现状与发展趋势[J].电讯技术,2014,54(7):1016-1024.
[22] 胡方强,吕涛,包亚萍.改进的自适应Kalman滤波在SINS/GPS组合导航中的应用[J].计算机工程与应用,2017,53(4):1-6.

