小辊径冷轧机组压扁系数模型及其影响因素
白振华 邢 雨 李柏阳 刘亚星 钱 承 赵伟泉
1.燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,0660042.燕山大学亚稳材料制备技术与科学国家重点实验室,秦皇岛,066004
0 引言
近年来,随着家电、汽车、包装等行业的迅猛发展,板带产品的需求日益扩大,市场竞争也日趋激烈。与此同时,在保证使用性能与产品质量的前提下,带钢越薄,用户使用成本越低,产品越有市场竞争力[1-7]。为了生产极薄带材,大中型钢铁企业一般采用多辊轧机进行轧制;受投资与维护成本的限制,大部分小型钢铁企业在无法配置多辊轧机的情况下往往依靠减小工作辊的辊径、采用“长径比”大且工作辊辊径绝对值较小的四辊或六辊轧机来生产。轧制过程中,此类轧机的工作辊前后张力差较大时,工作辊会产生较大的水平挠曲。这种水平挠曲的存在,使得工作辊与中间辊或支撑辊不再对称接触,辊间压扁系数也会发生相应的变化。肖宏等[8]通过建立有限元模型,来完成不同工况条件下的轧辊压扁的精确计算;白振华等[9]将轧辊压靠纳入考虑因素来提升轧机板形控制能力;郭立伟等[10]通过影响函数法来建立辊间压扁系数计算模型;杜凤山等[11]采用有限元法研究了六辊轧机对称轧制过程中的板形计算问题;ABDELKHALEK等[12]提出一种预测模型,预测薄板轧制过程中可能出现的板形缺陷。但人们在建立板形模型时一般都不考虑工作辊的水平挠曲问题,计算辊间压扁系数模型采用的都是对称接触模型[8-9,13]。这样,如何准确计算工作辊“长径比”大且辊径绝对值小的轧机的工作辊发生水平挠曲时的辊间压扁系数,就成为建立该类轧机板形模型、预报与控制该类轧机板形的基础。本文在此背景下,通过建立一套新的压扁系数计算模型,来解决水平挠曲时非对称的压扁系数计算问题。
1 辊间压扁系数模型的建立
1.1 辊间压扁宽度计算模型的建立
轧机工作辊的变形力主要包括竖直方向上的轧制压力、辊间压力与弯辊力,以及水平方向上的前后张力。轧制压力、辊间压力与弯辊力决定工作辊垂直于带钢方向的挠度,直接影响负载辊缝,同样,在前后张力的作用下,工作辊在平行于带钢方向也会发生挠曲变形,这种挠曲变形在小辊径冷轧机组当中更为突出,如图1所示。考虑到工作辊水平挠曲时,支撑辊或中间辊与工作辊将不再对称接触,其辊间压力在工作辊上的作用点也会发生偏移,造成辊间左右压扁宽度不再相等,因此以往的压扁宽度计算模型已不能适用于“长径比”大且辊径绝对值较小的工作辊。
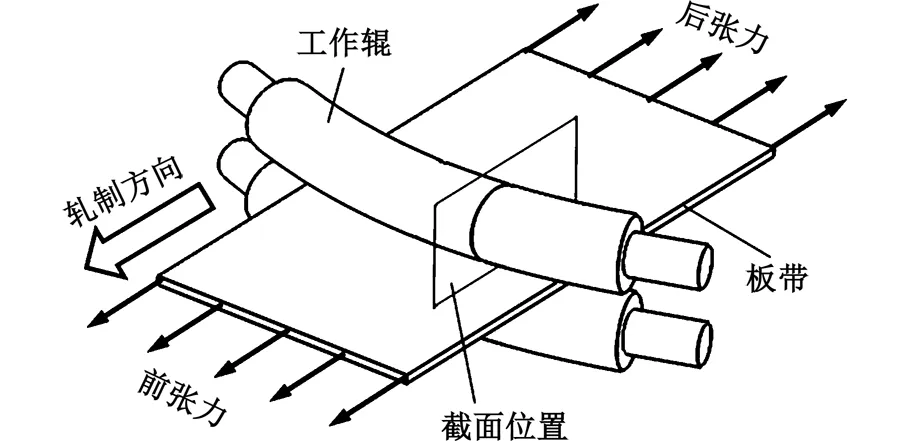
图1 工作辊水平挠曲示意图Fig.1 Schematic diagram of horizontal deflection of work roll
下面以六辊轧机为例,针对工作辊出现水平挠曲时的辊间压扁宽度进行推导计算,四辊轧机与之类似。为方便分析辊间压扁宽度,将工作辊沿辊身方向分成2n+1段,并以其中的第i段的横截面作为研究对象,如图2所示。将工作辊沿中间辊的中心线垂直分成左右两部分,那么工作辊i段横截面可看成是由小椭圆弧(左)与大椭圆弧(右)组成。
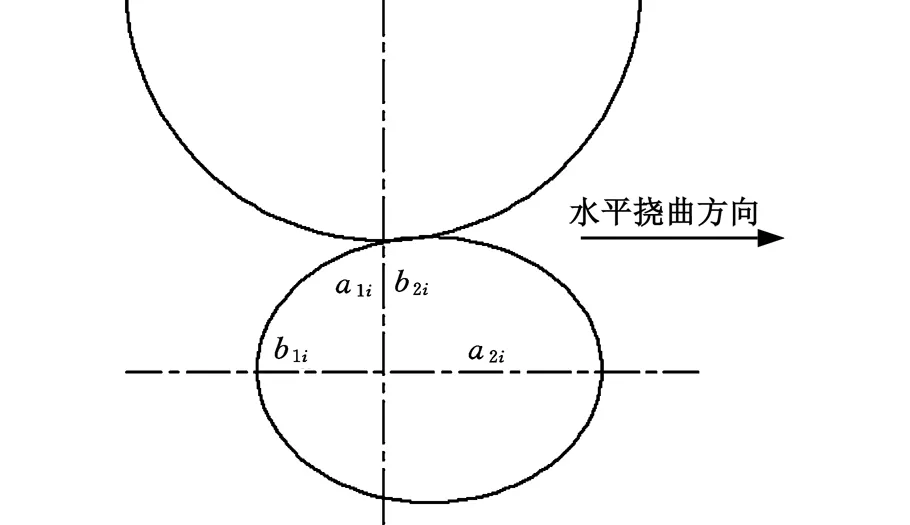
图2 第i单元工作辊与中间辊的不对称接触Fig.2 Asymmetic contact of rolls in unit i
根据图2中的几何关系,第i单元内,左右两个半椭圆的参数可表示为
(1)
式中,a1i、b1i分别为左侧椭圆的长轴和短轴长度,mm;a2i、b2i分别为右侧椭圆的长轴和短轴长度,mm;Rw为工作辊半径,mm;Δi为水平挠曲而引起的工作辊第i个单元与中间辊之间的“附加凸度”,mm;fw1i为工作辊第i个单元的水平挠曲,mm。
故两椭圆的曲率半径为
(2)
式中,ρ1i、ρ2i分别为左侧椭圆弧和右侧椭圆弧的曲率半径。
根据式(2)并对赫兹公式进行修正,即可计算出考虑工作辊水平挠曲时辊间压扁的左右宽度:
(3)
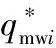
1.2 辊间接触变形模型的建立
将中间辊的应力分解成两个叠加的应力,如图3所示,其中,第一个可看作是半无限体受到轧辊间作用力q(kN)作用时所产生的压应力σ1,但轧辊外表面会产生一个压应力,为保持轧辊上的应力处于平衡状态,应该叠加第二个应力(拉应力)σ2。两个应力的函数表达式为
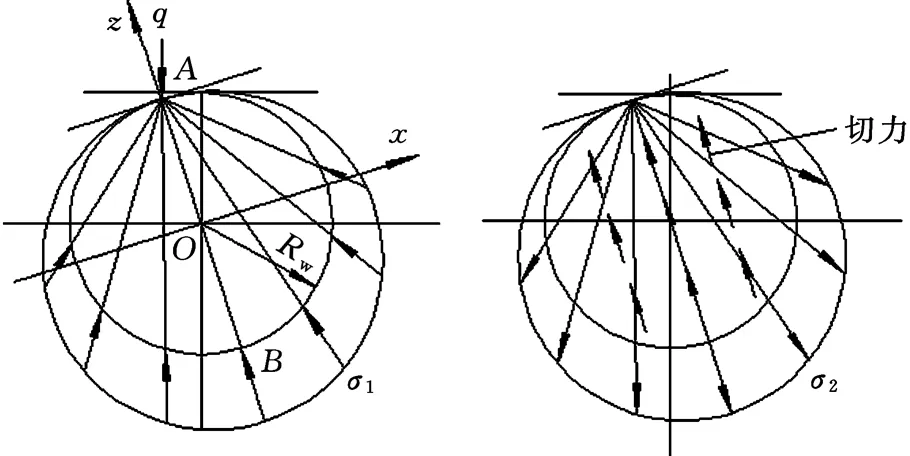
(a)正应力简图 (b)切应力简图图3 应力的叠加图Fig.3 Stress superposition diagram
(4)
式中,R为轧辊半径,mm;θ为所设定的应力函数的中间参数。
联立后得到合成的应力函数以及应力:
(5)
实际上,q应该是分布载荷p(ξ)而不是集中载荷,此时的载荷分布为非对称分布,而不再是以往的对称分布,故可对载荷分布曲线进行椭圆化处理,处理后的分布形式如图4所示,其中,分布载荷p(ξ)的表达式为
(6)
式中,k1、k2分别为左右载荷分布系数。
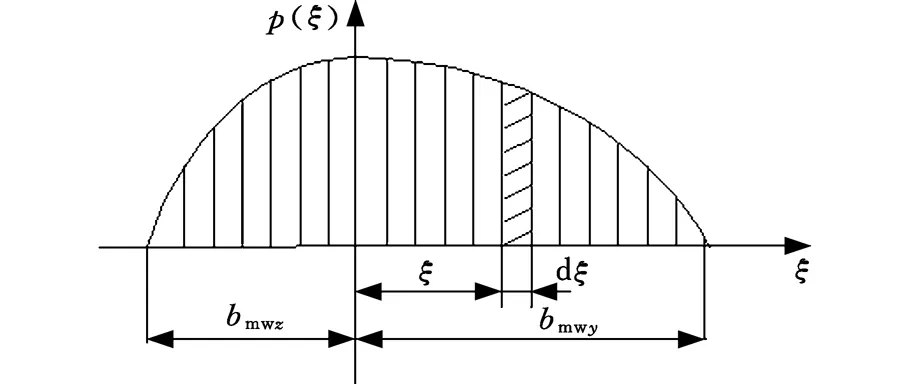
图4 载荷分布规律图Fig.4 Distribution law of load
对应区间上的总载荷与分布载荷的关系为
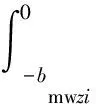
(7)
qmwi=0时,k1bmwzi=k2bmwyi,联立式(6)、式(7)得
(8)
(9)
(10)
故将应力函数(式(5))σx与σz中的qmwi用dq=pi(ξ)dξ代替,将x用x-ξ代替,之后在-bmwzi至bmwyi上进行积分,计算后得到
(11)
x=0时,z向、x向的应力分别为
(12)
对于平面情况(εy=0),z方向上的压缩变形为
(13)
把式(12)中的σx、σz代入式(13),分别从0至R以及从-R至0两个区间上积分,可得到图3a中的OA段承载区压缩变形量ΔR以及OB段非承载区的压缩变形量ΔR′,化简之后可得到:
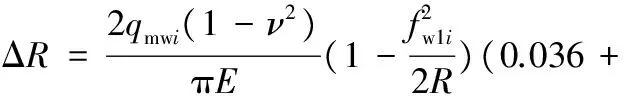
(14)
(15)
1.3 辊间压扁系数计算模型的建立
通过对工作辊发生水平挠曲时辊间接触情况的分析,得到承载区与非承载区的压缩变形量,最终得到辊间压扁系数模型。
对于中间辊而言,根据式(14)计算得到的压缩变形量为
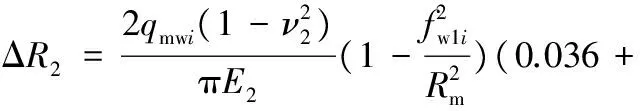
(16)
因为工作辊辊身的上下表面都存在载荷作用,所以工作辊的压缩变形量ΔR1由ΔR和ΔR′两部分组成,即有
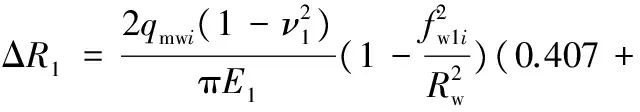
(17)
因此工作辊和中间辊第i段的压扁量为
f=ΔR1+ΔR2
(18)
工作辊和中间辊第i段之间的压扁系数Kmwi为
Kmwi=fcosαi/qmwi
(19)
2 辊间压扁系数的影响因素
在设备参数及轧制工艺参数确定的情况下,通过小辊径冷轧机组辊间压扁系数模型,并结合金属变形模型与辊系弹性变形模型的耦合[5-6]即可得出轧辊间的压扁系数及相关参数的数值。为进一步说明本模型的计算效果,以某钢厂450六辊轧机为例(机组的主要设备参数如表1所示),选取典型规格的产品(轧制工艺参数如表2所示),针对各影响因素进行分析说明,在分析过程中,只对其中某一个变量单独进行改变,保证其他参数不变。
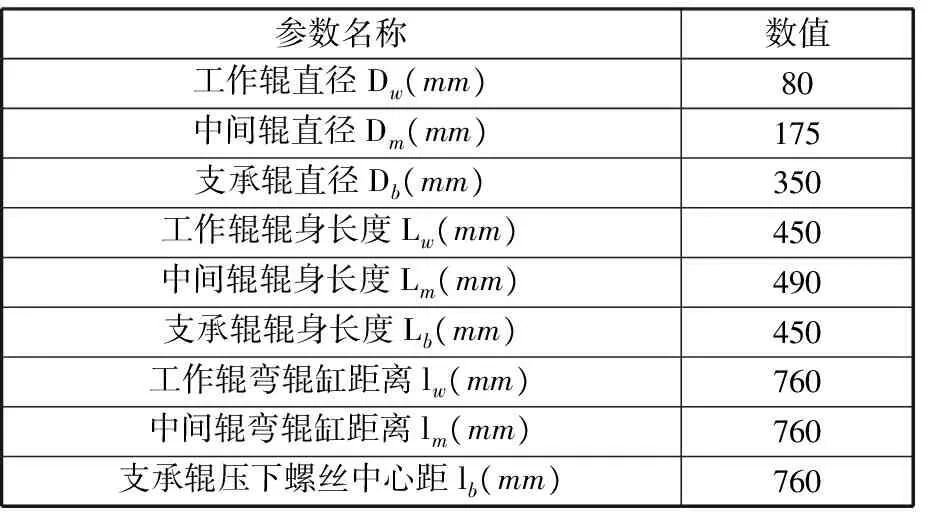
表1 某小型450六辊轧机主要设备参数
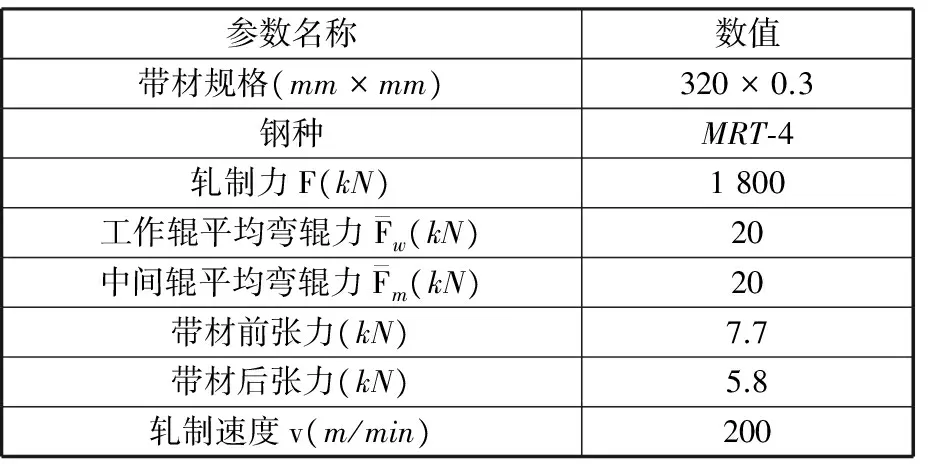
表2 典型规格产品轧制工艺参数
2.1 前后张力对压扁系数的影响
通过逐步增加前后张力差,计算出工作辊的水平挠曲分布值,如图5所示。由图5中可以看到,随着张力差绝对值|ΔFT|的逐步增大,工作辊水平挠度也逐渐增大。同时可以看到,在前后张力差一定的情况下,辊身中部水平挠度最大,说明此时轧机对板带中部浪形的控制效果最弱。
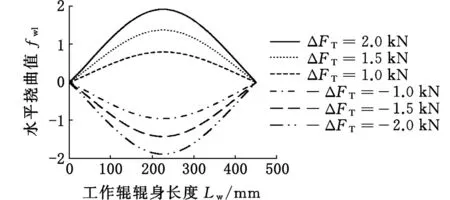
图5 不同前后张力差作用下工作辊水平挠度Fig.5 The horizontal crown of a work roll under varying degrees of difference between front and rear tension
由第1节可知,工作辊产生水平挠曲后,工作辊与中间辊的接触弧不再成对称分布。为更好地说明,在这里给出工作辊产生水平挠曲后的左右侧(以中间辊轴线为参照)接触弧长分布的计算结果,如图6所示。由图6可以看到,后张力大于前张力即前后张力差为负值时,左侧接触弧长大于右侧接触弧长;随着前后张力差的增大,左侧接触弧长逐渐减小,右侧接触弧长逐渐增大,其中,辊身中部的压扁系数变化速度最快,端部趋于稳定。
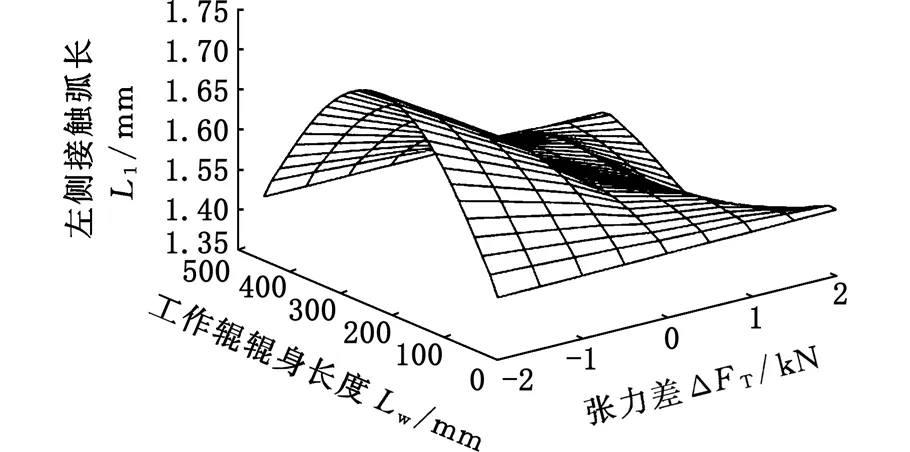
(a)左侧接触弧长
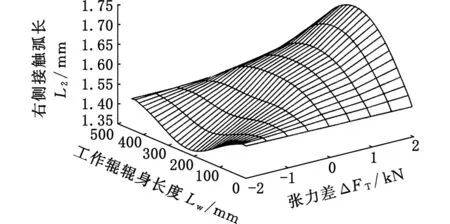
(b)右侧接触弧长图6 不同张力差作用下左/右侧接触弧长Fig.6 Left and right sides of the contact arc length under varying degrees of difference between front and rear tension
在得到左右接触弧长后,进一步计算便可得到压扁系数,如图7所示。由图7可以看到,当前后张力差增大时,辊身中部压扁系数快速减小;当前后张力趋于相等时,压扁系数也趋于平均。由于压扁系数受到左右侧接触弧长的共同影响,所以图7呈现一定的对称性。
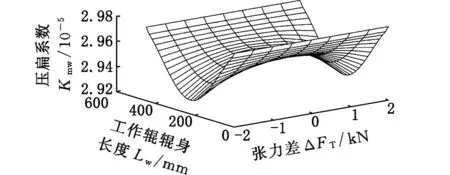
图7 不同张力差作用下工作辊与中间辊间压扁系数Fig.7 Flattening coefficient between the work roll and intermediate roll under varying degrees of difference between front and rear tension
2.2 工作辊直径对压扁系数的影响
在相同前后张力的作用下,工作辊的直径直接决定工作辊的挠曲程度,进而影响压扁系数的变化,即工作辊直径是压扁系数变化的根源之一,这一点在小辊径轧机上尤为突出。为了能更加清楚地说明小辊径轧机辊径变化对工作辊水平挠度及压扁系数的影响,在考虑轧辊的实际允许使用直径为70~100 mm的基础上,选定工作辊直径变化区间为60~100 mm,以10 mm为步长,同时保持其他工艺参数不变,分别计算出相应辊径下的水平挠曲曲线(图8)、左右接触弧长分布曲线(图9),以及压扁系数分布曲线(图10)。需要说明的是,60 mm辊径仅为本文理论计算所用,实际中并不使用,这也间接说明了辊径太小会直接影响带钢的出口板形质量。
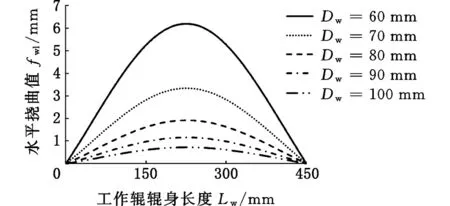
图8 不同工作辊直径对应的水平挠曲值Fig.8 Horizontal deflection corresponding to different work roll diameters

(a)左侧接触弧长
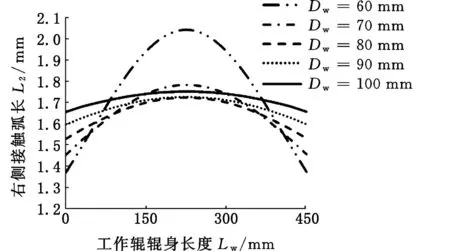
(b)右侧接触弧长图9 不同工作辊直径对应的左右接触弧长Fig.9 Left and right sides of the contact arc length corresponding to different work roll diameters
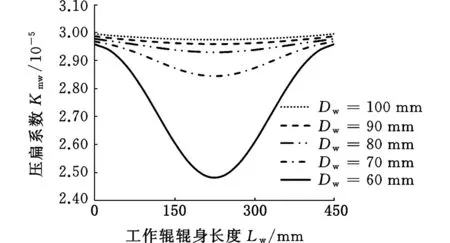
图10 不同工作辊直径作用下的压扁系数分布Fig.10 Flattening coefficient distribution corresponding to different work roll diameters
由图8可以看出,工作辊直径减小时,水平挠曲值快速增大,这说明直径越小的工作辊越容易发生水平挠曲,进而使得轧制后带材的边浪缺陷加剧,削弱了轧机对板形的控制能力。
由图10可以看到,工作辊直径逐渐增大时,轧辊中部压扁系数快速增大,最终压扁系数分布趋于均匀,在这个过程中,左右接触弧长的变化如图9所示。辊径较小时,左右侧接触弧长相差较大,而随着工作辊直径的增大,左右侧接触弧长差值逐渐减小,最终趋于相等。
2.3 弯辊力对压扁系数的影响
设定中间辊弯辊力为20 kN,工作辊弯辊力Fw依次变化并保持其他工艺参数不变,计算结果如图11所示。由图11可以看到,当弯辊力从50 kN依次变化到-50 kN时,辊间压扁系数逐渐趋于均匀,即从正弯辊向负弯辊变化过程中,边部压扁系数减小,中部压扁系数增大。

图11 不同弯辊力作用下压扁系数分布Fig.11 Distribution of the flattening coefficient under different bending roll forces
对工作辊进行正弯辊操作时,工作辊轴线为类似开口向上的二次曲线,工作辊与中间辊的接触压力分布为端部大于中部,因此端部的压扁系数比中部的压扁系数大;对工作辊进行负弯辊操作,在不考虑水平挠曲时,中部压扁系数应大于端部的压扁系数;当工作辊出现较大水平挠曲时,这种分布规律发生变化,负的弯辊力也只是在一定程度上使压扁系数分布趋于均匀,但依然是端部压扁大于中部。
2.4 不同带材宽度对压扁系数的影响
在保证单位张力以及其他轧制工艺条件不变的情况下,仅仅改变带材宽度b(此时带材厚度为0.3 mm),计算得到的结果如图12所示。
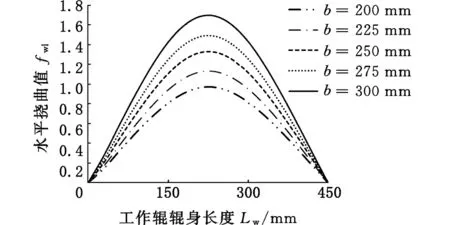
图12 不同带材宽度对应的水平挠曲值Fig.12 Horizontal deflection corresponding to different width of strip
由图12可以看到,随着带材宽度b的增大,工作辊的水平挠曲值也逐渐增大,同时,由图13可以看到工作辊与中间辊之间的压扁系数变化幅度更加剧烈。造成这种现象的原因在于,轧制相同材质和厚度的带材时,随着带材宽度的逐渐增大,带钢与轧辊间的压力逐渐增大。由于工作辊的水平刚度一定,而带材宽度的增大会使工作辊在水平方向上的载荷增大,使工作辊的水平挠曲程度加重,进而影响压扁系数的分布,这也从侧面反映出,在这种状态下,工作辊越靠近中部的地方受到的中间辊的支承作用越小,使得轧机对带材的板形控制能力也越弱。
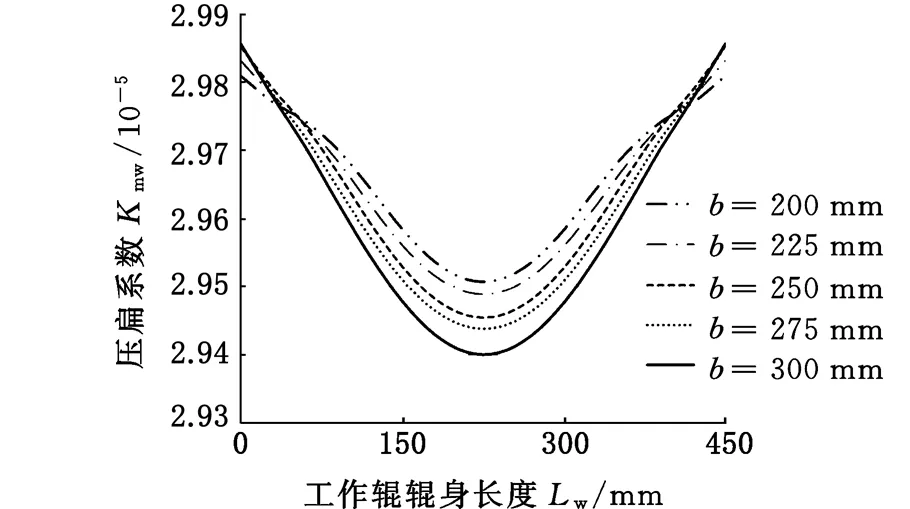
图13 不同带材宽度作用下压扁系数分布Fig.13 Distribution of the flattening coefficient under different width of strip
3 模型的实验及应用
在以往的生产过程中,一直认为以某钢厂450六辊轧机处于常态轧制,而没有考虑工作辊的水平挠曲,导致成品板带的板形质量难以提高。为此,运用本文所述的“小辊径冷轧机组辊间压扁系数模型”编制了“450六辊轧机辊间压扁系数及板形预报软件”,用于分析验证该六辊轧机改变弯辊、窜辊以及前后张力对板形的控制效果。
为了进一步说明本模型的实际效果,在此给出相关实验数据,表3给出了钢卷的基本参数,其材质均为MRT-4,钢卷编号第一位数字表示钢卷编号,第二位数字表示分卷号。分卷号为1的钢卷在原有模型指导下进行轧制,分卷号为2的钢卷在本模型指导下进行轧制。轧制后,对2个钢卷进行取样测量,对相关数据进行整理后得到浪高对比曲线(图14)、浪距对比曲线(图15),以及急峻度对比曲线(图16)。通过对比可以看到,在本模型指导下进行轧制的钢卷在浪高、浪距及急峻度方面有显著改善,说明本模型有助于提高轧机对于板形的控制能力,得到更好的板形质量。
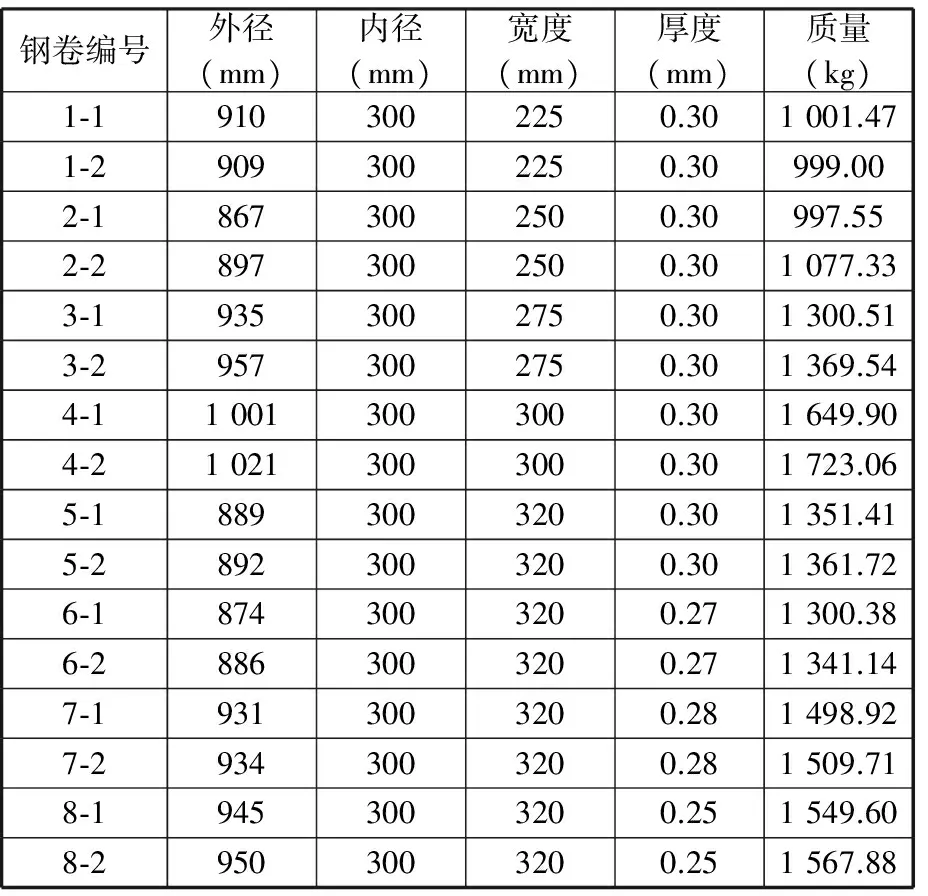
表3 钢卷的基本参数
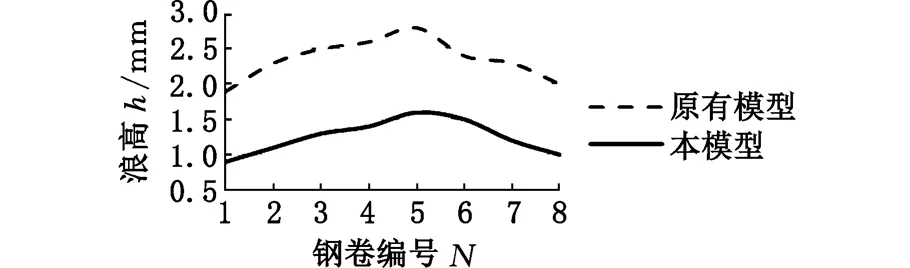
图14 浪高对比曲线Fig.14 Contrast curve of wave height
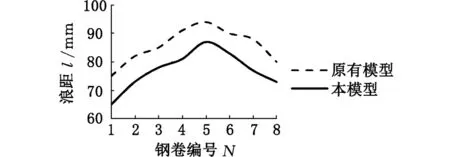
图15 浪距对比曲线Fig.15 Contrast curve of wave length
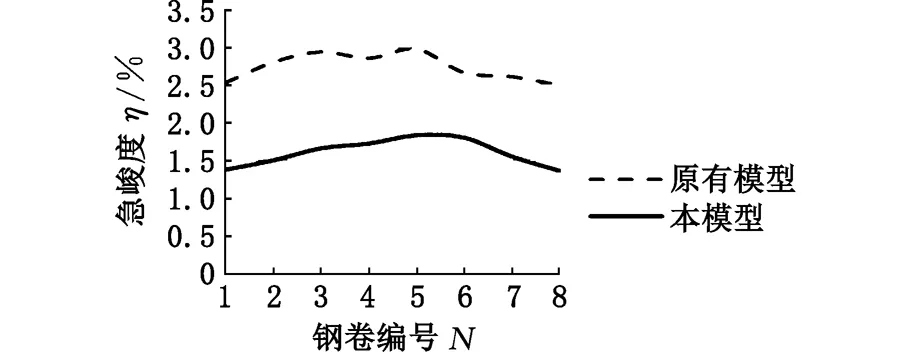
图16 急峻度对比曲线Fig.16 Contrast curve of urgency and severity
应用本模型之前,板形缺陷造成的板形封闭率约为5%,随着软件与现场系统的不断调试融合,封闭率逐步降低,最终的封闭率降低到1%以下。
4 结论
(1)结合轧机的设备与工艺特点,推导了工作辊“长径比”大且辊径绝对值小的轧机在工作辊发生水平挠曲时的辊间压扁系数模型,进一步精确计算了工作辊发生水平挠曲时的辊间压扁系数。
(2)在推导得到的模型的基础上,通过改变单一变量,对工作辊出现水平挠曲时的辊间压扁系数的影响因素进行了具体分析。从分析结果可以看出,工作辊直径、前后张力差对辊间压扁系数以及工作辊水平挠曲程度影响较为显著,对弯辊的影响相对较弱。因此,针对工作辊水平挠曲问题,在实际生产中对工作辊辊径及前后张力差进行调控是必不可少的控制手段,而弯辊控制则可以作为精细调整控制项目进行小范围调整。
[1] SUN Jianliang, PENG Yan, LIU Hongmin, JIANG Guangbiao. Vertical Vibration of Moving Strip in Rolling Process Based on Beam Theory [J]. Chinese Journal of Mechanical Engineering, 2009, 22(5):680-687.
[2] 张军良, 崔顺, 刘辉, 等. 板带轧机的发展历史与现状 [J]. 有色金属加工, 2011(6):1-6.
ZHANG Junliang, CUI Shun, LIU Hui,et al. Development History and Present Situation of Strip Mill [J]. Nonferrous Metal Processing, 2011(6):1-6.
[3] 刘连喜,刘建兵. 中国金属包装产业及包装材料的发展现状及趋势[J]. 河北冶金, 2015(7):76-79.
LIU Lianxi, LIU Jianbing. Development Situation and Trend of Metal Package Industry and Package Materials at Home [J]. Hebei Metallurgy, 2015(7):76-79.
[4] 计江,尤磊,刘云飞,等. 国产首套1200mm双机架四辊平整兼二次冷轧机组[J]. 冶金设备,2016(6):60-62.
JI Jiang, YOU Lei, LIU Yunfei,et al. Domestic First Set of 1200mm Two Tandem of 4-high Skin Pass and Double Cold-reduced Mill[J]. Metallurgical Equipment, 2016(6): 60-62.
[5] 王晓东, 黄久贵, 李建中, 等. 国内外镀锡板生产发展状况 [J]. 上海金属, 2008(4):45-48.
WANG Xiaodong, HUANG Jiugui, LI Jianzhong,et al. International and Domestic Development Station of Tinplate Steel [J]. Shanghai Metals, 2008(4):45-48.
[6] 薄炜. 电镀锡板工艺发展概况及展望[J]. 电镀与精饰, 2014(7):25-29.
BO Wei. DevelopmentOverview and Prospects of Manufacture Process of Tin-plating[J]. Plating & Finishing, 2014(7): 25-29.
[7] 赵智勇.国内镀锡板的生产与市场[J].中国冶金,2013(4):7-9.
ZHAO Zhiyong. Production and Market of Tin Plate in China [J]. China Metallurgy, 2013(4): 7-9.
[8] 肖宏,任忠凯,刘晓,等. 极薄带轧制变形区轧辊压扁试验与有限元模拟[J]. 钢铁,2017,52(1):38-42.
XIAO Hong, REN Zhongkai,LIU Xiao, et al. Experiment and Finite Element Simulation of Roll Flattening in Deformation Zone for Ultra-thin Strip Rolling[J]. Iron and Steel, 2017,52(1):38-42.
[9] 白振华,刘宏民,李秀军,等. 平整轧制工艺模型[M].北京:冶金工业出版社,2010
BAI Zhenhua, LIU Hongmin, LI Xiujun, et al. Flat Rolling Process Model[M]. Beijing: Metallurgical Industry Press, 2010.
[10] 郭立伟, 陈丹, 高雷,等. 六辊CVC辊系辊间横向轧制力分布的研究[J]. 冶金设备, 2010(2):15-19.
GUO Liwei, CHEN Dan, GAO Lei, et al. Research of Roll Force Distribution between Rolls on Six-high CVC Mill[J]. Metallurgical Equipment, 2010(2):15-19.
[11] 杜凤山,薛涛,孙静娜. 六辊CVC轧机轧辊弯曲和压扁变形的有限元分析[J]. 燕山大学学报, 2011, 35(5): 396-401.
DU Fengshan, XUE Tao, SUN Jingna. Finite Element Analysis of Roll Bending and Flattening Deformation of Six Roll CVC Mill[J]. Journal of Yanshan University. 2011, 35(5): 396-401.
[12] ABDELKHALEK S, MONTMITONNET P, LEGRAND N, et al. Coupled Approach for Flatness Prediction in Cold Rolling of Thin Strip[J]. International Journal of Mechanical Sciences, 2011, 53(9):661-675.
[13] 连家创, 刘宏民. 板形板厚控制[M]. 北京:兵器工业出版社, 1995.
LIAN Jiachuang, LIU Hongmin. Control on Thick and Shape of Strip[M]. Beijing: Arms Industry Press, 1995.

