基于递归小脑神经网络模型控制的空间机器人关节抗死区及摩擦控制
黄小琴 陈 力
1.福州大学机械工程及自动化学院,福州,350116 2.福州大学福建省高端装备制造协同创新中心,福州,350116
0 引言
在人类对太空探索的活动中,空间机器人发挥着愈来愈重要的作用。代替宇航员完成卫星的安装与修理,回收、补给燃料物资等舱外活动,都离不开空间机器人,它的使用可以大幅度降低探索太空的风险和成本,因此其动力学控制问题受到越来越多的关注[1-9]。文献[10]研究了初始动量矩不为零对空间机器人系统动力学行为的影响。文献[11]设计了基于速度观测器自适应控制方法,实现了柔性关节空间机械臂关节铰期望轨迹的跟踪及抑振。文献[12]采用前馈神经网络逼近空间机器人的未知动力学模型以完成轨迹跟踪控制。
以上这些控制方法均没有考虑关节力矩输出死区与摩擦对控制精度的影响。死区、摩擦非线性特性在执行器中常见并且不可避免,很多情况下,它们对高精度控制产生很大的影响。若不能消除其影响,除了影响稳态跟踪误差以外,还可能会产生极限环振荡,甚至造成控制失效,从而无法完成空间任务。因此,选择合适的死区与摩擦补偿方法来抑制或消除死区与摩擦非线性对空间机器人系统控制的影响具有十分现实的意义[13-15]。文献[16]将机械臂的死区与摩擦视为不确定项,设计了一种自适应H∞控制器进行补偿。文献[17]利用自适应模糊系统、状态观测器及参数估计器,设计了一种动态面滑模控制方法;文献[18]考虑机械臂存在摩擦及死区等复杂工况,提出了一种模糊神经网络反演控制器。
上述研究均基于地面机器人模型,而在太空环境中,空间机器人的载体处于自由漂浮状态,载体与臂杆之间存在着强烈的动力学耦合作用,系统呈现出非完整的动力学性质。同时考虑到载体携带的燃料的有限性,相当有必要使用载体位置、姿态均不受控制的空间机器人系统。再者,由于系统存在外部干扰、负载改变、燃料消耗等变化,这使得其动力学模型参数具有不确定性,从而降低系统的控制精度,影响控制性能。综合以上各种原因,通常用于地面机器人的控制方法无法直接运用于漂浮基空间机器人的控制。
本文在上述研究的基础上,研究了漂浮基空间机器人存在关节力矩输出死区、摩擦及外部干扰情况下的轨迹跟踪问题。在系统参数、死区宽度与摩擦参数不确定的情况下,利用递归小脑神经网络模型来逼近包含摩擦误差及外部干扰在内的动力学方程不确定项,设计自适应死区预补偿器消除关节力矩输出死区的影响,利用摩擦双观测器估计不可测的内部摩擦状态。仿真算例证实了所设计方案的有效性。
1 系统动力学方程
图1所示为做平面运动的漂浮基刚性两杆空间机器人系统。
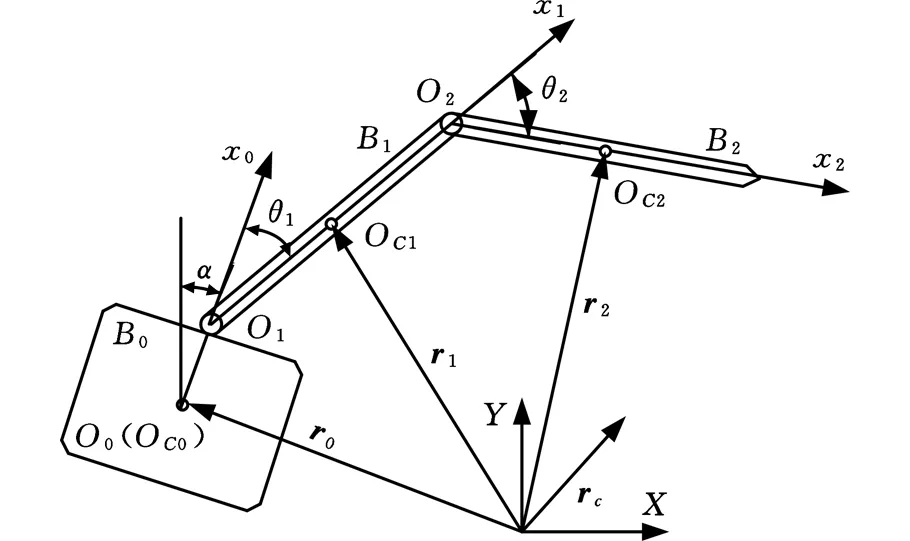
图1 漂浮基空间机器人系统Fig.1 Free-floating space robot system
应用系统动量守恒关系及拉格朗日第二类方程,可以得到带有外部干扰、摩擦力矩的载体位置、姿态均不受控的漂浮基空间机器人系统欠驱动形式的动力学方程:
(1)
q=[α0θT]T=[α0θ1θ2]T
τ=[τ1τ2]T∈R2

由于难以获得系统动力学模型精确的参数,因此式(1)可改写为
(2)

2 关节力矩输出死区及LuGre摩擦模型
2.1 关节力矩输出死区
“死区”是在关节的输入大小达到某个特定值之前,其输出为零的输入-输出关系。“死区”显示出的其实是一种“信息的损失”。本文考虑图2所示的死区模型,死区输入τd=[τd1τd2]T,输出τ=[τ1τ2]T中元素τi(i=1,2)的表达式为
(3)
其中,di-、di+分别为死区的左右宽度参数,di-,di+>0且不一定相等,但有界。

图2 关节力矩输出死区模型Fig.2 Joint torque output model with the dead-zone
把不对称死区模型写成以下形式[19]:
τ=W(τd)=τd-sat(τd)
(4)
sat(τd)=[sat1(τd1)sat2(τd2)]T
(5)
i=1,2
其中,死区宽度D=[d+d-]T,d+=diag(d1+,d2+),d-=diag(d1-,d2-)。


图3 自适应死区补偿原理图Fig.3 Adaptive dead-zone compensation principle
过死区前,先对力矩w进行死区补偿[19]:
(6)
式中,w为死区补偿前的力矩向量。
w通过死区补偿之后得到力矩τd,τd通过死区,所得到的τ为[19]

(7)
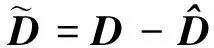
2.2 LuGre摩擦模型
摩擦力广泛存在空间机器人系统中,影响着系统的控制性能和精度,因此需要对关节未知摩擦进行补偿。LuGre摩擦模型能较为全面地描述摩擦力的动静态特性,因此本文选择LuGre摩擦作为两关节的摩擦模型。
LuGre摩擦模型表达式为
(8)
(9)

摩擦力可表示为
(10)
式中,σ1i为弹性阻尼系数,σ1i>0;σ2i为黏滞摩擦系数,σ2i>0。
根据式(8)、式(9),式(10)可改写为
(11)
σ3i=σ0iσ1iσ4i=σ1i+σ2i
在LuGre摩擦模型中,z是不可直接测量的内部摩擦状态,需要通过观测器对其进行估计,z估计较为困难,因此设计了两个摩擦观测器:
(12)
(13)

定义观测器估计误差:
(14)
(15)
LuGre摩擦力估计值可写为
(16)

3 递归CMAC神经网络控制方案
3.1 递归CMAC神经网络
小脑模型关节控制器(cerebellar model articulation controller,CMAC)神经网络是不依赖逼近对象的数学模型,具有良好的知识表达能力与泛化能力、优良的自学习及自适应能力等特点,其收敛速度比普通BP算法快得多,且避免了局部极小的问题。传统CMAC神经网络架构是前馈网络,缺点是仅适用于静态问题,而递归结构的CMAC神经网络具有动态特性,能够以任意精度逼近任意非线性动态系统。因此,本文采用递归CMAC进行控制方法设计,图4为其原理图。

图4 递归CMAC神经网络原理图Fig.4 Architecture of a recurrent CMAC neural network
递归CMAC网络各层的含义分述如下:
(1)输入区域。输入向量为x=(x1,x2,…,xna)T∈Rna。每个输入变量量化为离散的区块。
(2)联想记忆区域。na个输入离散为na个块,每个块的元素数为nb,nb≥2。第i个变量的第j个的接受域基函数为
(17)
hij=xi+rijφij(t-T)j=1,2,…,nb
其中,mij为基函数的中心值;vij为方差;rij为递归权重系数;φij(t-T)表示时间延迟T后φij(t)的值。
(3)接受域空间。接受域的个数为nc,nc=nb,此时接受域函数如下:

(18)
多维的接受域函数的列向量为
Φ=(b1,b2,…,bnc)T
(19)
(4)权值域。接受域和输出域之间的连接权值矩阵为
W=[W1W2…Wn0]
(20)
Wi=[W1iW2i…Wnci]T∈Rnc
式中,Wki为第i个输出变量的第k个接受域的权重值,i=1,2,…,nc。
(5)输出域。递归CMAC神经网络的输出为
y=WTΦ
(21)
W∈Rnc×noΦ∈Rnc×1
3.2 控制器设计
在太空环境下对空间机器人载体的位置、姿态均不加以控制,能够减少燃料的消耗,延长在轨空间使用寿命,因此,设计控制方案时应当给予考虑。
系统控制输出θ=[θ1θ2]T,而系统广义坐标向量q∈R3。显然,控制输出的维数小于q的维数,这样将使得我们难以继续利用式(1)及其相关性质进行后续相关控制器设计。为此,我们引入增广变量思想来解决这一难点。

(22)
定义滤波轨迹误差为
(23)
其中,下标r表示相应的后二阶向量;Λ、Λ2为对称,正定常值矩阵Λ∈R3×3,Λ2∈R2×2。
控制目标是设计控制力矩w,使得两关节铰的θ能够以较高精度达到期望轨迹。
理想的控制律为
(24)
其中,K为对角正常数矩阵,且K∈R3×3;ww为包含摩擦误差及外部干扰在内的动力学方程不确定项。用递归CMAC神经网络来逼近ww,输入为滤波轨迹误差s=[0s1s2]T,na=3,每个离散块取nb=nc=5,no=3。ww的最优逼近为
(25)
其中,W*为W的最优值;ε为最优逼近误差;‖ε‖≤ρ。则增广的控制规律可改写为
(26)

将式(26)、式(7)代入式(2),得到误差方程:
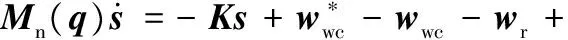
(27)
将LuGre摩擦值(式(11))与LuGre摩擦估计值(式(16))相减可得

(28)
定理对于式(1)所示的空间机器人系统,采用式(26)的控制规律及如下自适应调节律:
(29)
wr=ρs/‖s‖
(30)
死区宽度自适应律:
(31)
摩擦参数自适应律:
(32)
(33)
(34)
η0∈R5×5Ξ∈R4×4k>0
将使滤波误差s最终一致有界,即跟踪误差e收敛到零的一个任意小邻域。
证明构造李雅普诺夫函数

(35)
把V对时间t求一阶导数,可得
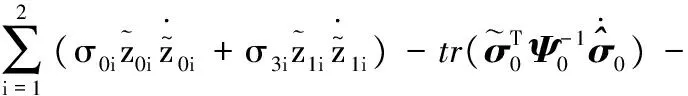
(36)
将误差方程(式(27))、自适应律(式(29)~式(34))、观测器估计误差(式(14)~式(15))、LuGre摩擦值差值(式(28))代入式(36),整理可得

(37)
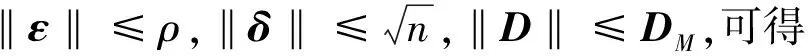

(38)
其中,Km=σmin(K)为矩阵K的最小奇异值; ‖sr‖=‖s‖。
最终得到

(39)
即
(40)

4 仿真算例
以图1给出的动力学模型为例,采用式(26)和式(29)~式(34)进行系统仿真。取如下系统惯性参数:l0=1.5 m,l1=l2=1 m,m0=40 kg,m1=2 kg,m2=1 kg。中心惯量矩J0=34.17 kg·m2,J1=J2=1.5 kg·m2。
空间机器人两关节铰的期望运动轨迹为
系统的外部干扰为
仿真初始值为
q(0)=[2 0.5 1.5]T
摩擦初始值为
死区宽度估计为
整个追踪过程所用时间t=20 s。
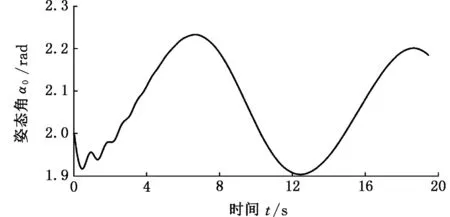
图5 载体姿态角的轨迹图Fig.5 Trajectory tracking of the base’s attitude

图6 两关节铰的轨迹跟踪图Fig.6 Trajectory tracking of the two joints
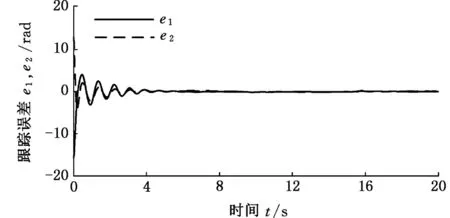
图7 两关节铰的跟踪误差图Fig.7 Trajectory error tracking of the two joints
图5~图7分别为存在关节力矩输出死区、摩擦与外部干扰的情况下,采用递归CMAC神经网络自适应控制方案的空间机器人载体实际运动姿态轨迹、两关节铰的实际运动轨迹(实线)与期望运动轨迹(虚线)及其跟踪误差图,从这3张图的仿真结果可以看出:控制方案虽然没有控制载体姿态,但其姿态变化平稳;空间机械臂两关节铰的实际运动轨迹能很好地跟踪上期望轨迹。
为对比控制方法的有效性,图8~图10给出了关闭死区补偿、关闭摩擦补偿与同时关闭死区和摩擦补偿之后各自的两关节轨迹图。从仿真结果明显可以看出,关闭死区补偿、关闭摩擦补偿之后,空间机械臂两关节铰始终无法跟踪期望轨迹,当同时关闭死区补偿与摩擦补偿之后,轨迹的偏差更大。

图8 两关节铰的轨迹跟踪图(关闭死区补偿)Fig.8 Trajectory tracking of the two joints (off dead-zone compensation)

图9 两关节铰的轨迹跟踪图(关闭摩擦补偿)Fig.9 Trajectory tracking of the two joints (off friction compensation)

图10 两关节铰的轨迹跟踪图(同时关闭死区与摩擦补偿)Fig.10 Trajectory tracking of the two joints (off dead-zone and friction compensation simultaneously)

表1关节铰轨迹跟踪的平均绝对误差

Tab.1 Mean absolute error of trajectory tracking rad
5 结论
(1)考虑空间机器人控制过程中存在关节力矩输出死区、摩擦与外部干扰的实际情况,设计了递归CMAC神经网络控制器与死区补偿估计器,使得两关节铰能够协调地跟踪期望运动轨迹。
(2)在系统惯性参数、死区宽度与摩擦参数不确定的情况下,设计了摩擦双观测器估计不可测的内部摩擦状态变量;应用死区预补偿器消除了关节力矩输出死区的影响;使用小脑神经网络模型逼近了包含摩擦误差及外部干扰在内的动力学方程不确定项,并采用自适应规律调整死区宽度、LuGre摩擦参数。
(3)李雅普诺夫理论证明了滤波误差是最终一致有界的,即跟踪误差会收敛到零的一个任意小邻域。
(4)从计算机仿真结果图看出,在关节力矩存在死区与摩擦的情况下,不进行补偿会严重影响控制精度,同时也表明了所提出控制方法的有效性。
[1] ABAD A F,MA O,PHAM K,et al. A Review of Space Robotics Technologies for On-orbit Servicing[J]. Progress in Aerospace Sciences,2014,3(2):1-26.
[2] 丁希仑,战强,解玉文.自由漂浮的空间机器人系统的动力学奇异特性分析及其运动规划[J].航空学报,2001,5(5):474-477.
DING Xilun,ZHAN Qiang,XIE Yuwen. Dynamic Singularity Analysis and Motion Planning of Free-floating Space Robot Systems[J]. Journal of Astronautics,2001,5(5):474-477.
[3] 程靖,陈力. 空间机器人双臂捕获卫星力学分析及镇定控制[J]. 力学学报,2016,48(4):832-842.
CHENG Jing,CHEN Li.Mechanical Analysis and Calm Control of Dual-arm Space Robot for Capturing a Satellite[J].Chinese Journal of Theoretical and Applied Mechanics,2016,48(4):832-842.
[4] 梁捷,陈力. 柔性空间机械臂末端运动及柔性振动的模糊自适应补偿控制 [J].兵工学报, 2011,32(1):45-57.
LIANG Jie,CHEN Li. Fuzzy Logic Adaptive Compensation Control of End-effect Motion and Flexible Vibration for Space-based Flexible Manipulator[J].Acta Armamentarii,2011,32(1):45-57.
[5] 洪在地,贠超,陈力.柔性臂漂浮基空间机器人建模与轨迹跟踪控制[J].机器人,2007,29(1):474-477.
HONG Zaidi,YUN Chao,Chen Li.Modeling and Trajectory Tracking Control of a Free-floating Space Robot with Flexible Manipulators[J]. Robot,2007,29(1):474-477.
[6] 张帆,黄攀峰.空间绳系机器人抓捕非合作目标的质量特性参数辨识[J].宇航学报,2015,36(6):630-639.
ZHANG Fan,HUANG Panfeng.Inertia Parameter Estimation for a Noncooperative Target Captured by a Space Tethered System[J].Journal of Astronautics,2015,36(6):630-639.
[7] 潘冬,赵阳,王兴贵,等.反作用轮铰间隙对航天器动态特性影响分析[J].振动与冲击,2012,31(13):71-75.
PAN Dong,ZHAO Yang,WANG Xinggui,et al.Influence of Joint Clearance in Reaction Wheel Dynamic Characteristics of Satellite[J].Journal of Vibration and Shock,2012,31(13):71-75.
[8] 陈志勇,陈力.漂浮基带柔性铰空间机器人的动力学建模及奇异摄动控制研究[J].中国机械工程,2011,22(18):2151-2155.
CHEN Zhiyong,CHEN Li.Study on Dynamics Modeling and Singular Perturbation Control of Free-floating Space Robot with Flexible Joints[J]. China Mechanical Engineering,2011,22(18):2151-2155.
[9] 黄小琴,陈力.存在未知死区的漂浮空间机械臂积分变结构模糊自适应控制[C]//第四届载人航天学术大会论文集. 哈尔滨,2016:51-55.
HUANG Xiaoqin,CHEN Li.Integral Variable Structure Fuzzy Adaptive Control for the Free-Floating Space Manipulator with Unknown Dead-Zone [C]//Proceeding of the Fourth Manned Space Conference. Harbin,2016:51-55.
[10] NANOS K,PAPADOPOULOS E.On the Use of Free-floating Space Robots in the Presence of Angular Momentum[J].Intelligent Service Robotics,2011,4(1):3-15.
[11] YU Xiaoyan,CHEN Li.Modeling and Observer-based Augmented Adaptive Control of Flexible-joint Free-floating Space Manipulators[J].Acta Austronautica,2011,4(1):3-15.
[12] KUMAR N,PANWAR V,BORM J H,et al.Adaptive Neural Controller for Space Robot System with an Attitude Controlled Base[J].Neural Computing and Applications,2013,23(7):2333-2340.
[13] HSU C F,KUO T C.Intelligent Complementary Sliding-mode Control with Dead-zone Parameter Modification[J].Applied Soft Computing,2014,6(8):355-365.
[14] HE Wei,AMOATENG O D,ZHAO Yin,et al.Neural Network Control of a Robotic Manipulator with Input Dead-zone and Output Constraint[J].IEEE Transactions on Systems, Man, and Cybernetics: Systems,2015,46(6):759-770.
[15] ISHIHARA A K,DOORNIK J V,MENAHEM S B.Control of Robots Using Radial Basis Function Neural Networks with Dead-zone[J].International Journal of Adaptive Control and Signal Processing,2011,25(7):613-638.
[16] KAZUYA S,HIROSHI M,KAZUHIRO T.An AdaptiveH∞Control for Robotic Manipulator with Compensation of Input Torque Uncertainty[C]//Proceedings of the 17th World Congress the International Federation of Automatic Control.Seoul, 2008:8919-8924.
[17] PARK S H,HAN S I.Robust-tracking Control for Robot Manipulator with Dead-zone and Friction Using Back-stepping and RFNN Controller[J].IET Control Theory and Applications,2011,5(12):1397-1417.
[18] CHEONG J Y,HAN S I,LEE J M.Adaptive Fuzzy Dynamic Surface Sliding Mode Position Control for a Robot Manipulator with Friction and Dead-zone[J].Mathematical Problems in Engineering,2013,2013(4):1-15.
[19] WANG Zhonghua,YANG Bo,CHENG Lin,et al.Robust Adaptive Dead Zone Compensation of DC Servo System[J]. Control Theory and Applications,IEE Proceedings,2006,153(6):709-713.

