多车场与多车型车辆路径问题的多染色体遗传算法
陈呈频 韩胜军 鲁建厦 陈青丰 王 成
浙江工业大学工业工程研究所,杭州,310014
0 引言
车辆路径问题(vehicle routing problem,VRP)是运输组织优化的核心问题。从现有研究文献看,围绕车辆路径问题的研究比较多,但多数是从以下三个方向进行研究:单车型或多车型的车辆路径问题[1-2],单车场或多车场的车辆路径问题[3-4],带时间窗或不带时间窗的车辆路径问题[5-6]。这主要是因为车辆路径问题属于NP难题,该问题只有在规模较小时才有可能求得其精确解,随着问题规模的扩大,求解难度急剧增加,往往很难求得最优解。多车场、多车型车辆路径问题(multiple-depot multiple-type vehicle routing problem,MDMTVRP)既是对基本车辆路径问题的扩展,更是对多车场车辆路径问题和多车型车辆路径问题的组合,它的求解必然更加复杂,目前还没有成熟的求解算法。
SUREKHA等[7]在研究多车场车辆路径问题时,根据C-W节约算法将客户就近分配给车场,然后采用遗传算法安排车辆配送路线。SALHI等[8]研究了带回程取货的多车型车辆路径问题并建立其数学模型,提出一种基于集合分割的启发式算法来求解该类问题。马建华等[9]采用变异蚁群算法求解MDMTVRP,对给定的顾客顺序划分车辆和指派车场,把该问题转化为寻找最优顾客顺序问题进行求解。然而,这种方法最大的缺陷在于,即使每条线路都最优,但从问题的整体而言,得到的却未必是全局最优解。罗鸿斌[10]将改进粒子群算法用于求解MDMTVRP,粒子采用3个n维向量进行编码的方式,但造成了大量的无效运算,导致求解效率不高。SUNDAR等[11]研究了附加燃料限制的MDMTVRP,通过比较4种基于节点和基于弧的模型,设计了分支切割算法,不过该方法很难应用于规模较大的情况。
大量的文献均表明,多车场、多车型车辆路径问题,特别是规模较大的多车场、多车型车辆路径问题的求解效率和解的质量还远未达到实用要求。为此,本文提出一种求解MDMTVRP的多染色体遗传算法。
1 MDMTVRP描述和数学模型
1.1 问题描述
MDMTVRP可以描述为:拥有多种车型车辆的多个车场需要对服务区内的众多客户提供配货服务,要求通过合理地调度车辆并选择适当的行车路线,使总配送费用最低。该问题有如下几个基本假设[12]:①多个车场拥有多种车型的车辆;②车型不同,车辆的装载量可能不同;③车型不同,车辆的成本(固定成本和可变成本)可能不同;④一辆车最多被调度一次,从车场出发并最终返回原车场;⑤一辆车至少可以服务一个客户,即一个客户的需求量不会大于一辆车的装载量;⑥一个客户被且仅被一辆车服务。
1.2 数学模型
无论是MDMTVRP,还是基本车辆路径问题,一辆车必然属于某个车场,同时也必然属于某个车型。因此,本文直接为客户和所有车辆进行统一编号,从而能够利用只包含3个角标的变量建立MDMTVRP的数学模型(传统的建模方式中,变量需要使用4个角标表示),有效地简化了模型。
设多个车场拥有不同型号的车辆共H辆,每辆车的坐标位置反映其所属车场信息,装载量和成本反映其所属车型信息,车的装载量为Qh(h=1,2,…,H),固定成本为c1h,行驶单位距离的可变成本为c2h,客户n的需求量为gn(n=1,2,…,N)。MDMTVRP可以用一个加权图G(V,E)来表示,其中,节点集V={1,2,…,N+H},V的前N个节点表示客户,后H个节点表示车辆;路径集E={dij|i,j∈V}表示从节点i到节点j的距离集合。问题的目标是要在满足约束条件下找到一个车辆集和路径集,使总配送费用最低。
引入决策变量:
(1)
基于上述条件,MDMTVRP的数学模型可表示如下:
目标函数
(2)
约束条件
(3)
(4)
(5)
(6)
(7)
(8)
上述模型中,式(2)表示最低配送成本,前半部分为固定成本,后半部分为可变成本;式(3)表示调度车辆数不超过车辆总数;式(4)、式(5)表示一个客户仅被一辆车配送一次;式(6)表示每辆车的配送总量不超过其最大装载量;式(7)表示车辆从车场出发并返回原车场;式(8)表示车辆不能从一个车场行驶到另一个车场。
需要说明的是,本文建立的三角标变量的数学模型基础性和通用性较强。实际上,许多MDMTVRP的扩展问题也能通过上面的模型进行求解,例如约束条件中考虑客户优先顺序、车辆行驶时间、货物成本因素,以及优化目标为车辆数最少、行驶路径最短、客户等待时间最短等多车场、多车型车辆路径问题。
2 多染色体遗传算法
虽然遗传算法传统的单染色体(单链)编码方式在求解基本的单车场单车型车辆路径问题上有着较好的效果,但对于MDMTVRP,由于添加“多车场”和“多车型”两个重要约束,往往会导致解的质量不高,还会产生大量的不可行解甚至非法解,大大降低了求解效率。
针对上述问题,本文从遗传算法设计的本源出发,对遗传算法进行了重新设计。为此,联系到MDMTVRP,本文从更加贴近生物遗传进化规律的角度,提出了求解该问题的多染色体编码方式,即一个个体包含多条染色体,染色体的数量与车辆总数相等,每条染色体恰好完全表示一辆车的行驶路线,既方便了染色体的交叉,又能避免不可行解甚至非法解的产生。由于该算法的设计思想与传统的一个个体只含有一条染色体的遗传算法不同,所以,本文把该种求解MDMTVRP的遗传算法命名为多染色体遗传算法。
2.1 染色体的编码
遗传算法求解MDMTVRP时,染色体的编码是一项非常重要的工作,它直接决定了算法性能的优劣。由于一辆车必然对应某个车场和车型,也必然对应一条配送路线,所以,本文设计种群个体染色体数量等于车辆数量的多染色体编码方式。对于一个包含N个客户、H辆车的MDMTVRP,将客户编号为自然数1~N,车辆编号为自然数N+1~N+H,每个自然数表示一个基因。种群中每个个体包含H条染色体,每一条染色体的第一个基因代表车辆(称为车辆基因),其他基因代表客户(称为客户基因),基因的顺序代表被服务的先后。
例如,如图1所示,有两种车型(Ⅰ型、Ⅱ型)的5辆车(编号11~15)分别属于3个车场(编号A、B、C),要为10个客户(编号1~10)提供配送服务。个体设计为与车辆数相等的5条染色体,编码为:11,9,1,3;12,6,8;13,10,7;14;15,5,4,2。
染色体表示意义如下:车辆11从车场出发依次为客户9、1、3提供服务,然后返回原车场;车辆12从车场出发依次为客户6、8提供服务,然后返回原车场;车辆13从车场出发依次为客户10、7提供服务,然后返回原车场;车辆14未被调用;车辆15从车场出发依次为客户5、4、2提供服务,然后返回原车场。

图1 车辆配送示意图Fig.1 Schematic diagram of vehicle distribution
2.2 初始种群的确定
随机产生一个种群规模为S的初始种群,具体过程如下:随机打乱序列{1、2、…、N}的顺序,然后随机选择编号N+1~N+H中的一个编号(代表车辆),序列的第一个编号对应的客户“试分配”给这辆车,如果不超载,则此客户确定被分配给这辆车,否则在其余车辆中随机选择一辆并再次判断是否超载;以此类推,直至将此客户分配给某辆车。按上述过程依次将新序列的剩余客户分配给车辆。客户被分配给车辆的先后顺序作为被服务的次序。
2.3 适应度函数
遗传算法用适应度来评价个体的优劣程度,对于极大值问题,适应度越大的个体越好;对于极小值问题,适应度越小的个体越好。由于种群中不存在不可行解和非法解,所以直接根据式(2)计算对应的目标函数值zi(i=1,2,…,S),并将其作为个体i的适应度。
2.4 交叉操作
由于不定点交叉或多点交叉可能会导致车辆超载,从而产生非法解,所以本文采用定点单点交叉,交叉点设定在第一个基因(车辆基因)之后。根据交叉概率Pc随机选择个体A、B,对其进行交叉操作的具体步骤如下:
(1)随机产生一个介于1~H之间的自然数,代表要进行交叉操作的两个个体的同一染色体编号(个体A编号设为a,个体B编号设为b,且a=b);
(2)取出a、b两条染色体相同的客户基因存入基因库Fab中,不同的客户基因分别存入基因库Fa、Fb中;
(3)交换2条染色体的客户基因(保持客户基因的顺序不变);
(4)将个体A中除染色体a以外的其他染色体的客户基因与Fb的基因逐一进行比对,并将所有相同的基因删除,同样,对个体B进行类似操作;
(5)将Fa中的基因逐一随机插入个体A任意染色体的首基因之后的任意位置。之后,判断车辆是否超载:如果超载,则随机插入下一条染色体并再次判断是否超载,以此类推,直至将Fa中的基因全部分配出去为止。对个体B进行类似操作。
2.5 变异操作
设变异概率Pe,个体每条染色体第一个基因不产生变异,对于其他的每个基因i,在区间0~1之间随机产生浮点数ri与基因i对应。如果ri 传统的正比选择法(选择概率正比于个体的适应度)有一些不好的性质:迭代早期,一些适应度很高的超级个体会霸占选择过程,导致选择压力过大;迭代晚期,个体间的适应度差距较小,导致选择压力过小。CHENG等[13]提出的正规化技术弥补了上述不足,它的形式如下(对于极小化问题): (9) 设计第S+1个个体,最初用来保存初始种群中的最优个体。之后,如果第S+1个个体的适应度优于所有子代个体,则用它替换掉子代中的最差个体;否则,它被子代中的最优个体取代。精英选择一方面可以保证优秀个体的基因在进化选择过程中不被丢失,从而加速收敛;另一方面确保了子代种群中的最优个体不会比父代种群差,从而使进化曲线单调下降。 为了验证多染色体遗传算法的可行性及有效性,对一个随机生成的算例进行求解验证。算例中采用直线距离,便于更直观地说明问题,系统内的车场和客户的位置随机分布在100 km×100 km的区域内。设有3个车场、3个类型的车辆(共10辆)为30位客户配送货物,其信息分别见表1和表2。要求安排适当的车辆及其行驶路线,使配送任务的总费用最少。 需要指出的是,车辆服务客户的数量可能不同,如果使用染色体编码常用的数组结构表示染色体,则必须根据染色体的最大长度设定数组长度,这必然会造成大量的无效运算和资源浪费。为了解决这个问题,本文采用链表结构表示染色体,染色体中基因的顺序通过链表中的指针链接次序实现,从而方便基因的插入和删除操作,其时间复杂度达到O(1),数组结构进行同样操作的时间复杂度为O(n)。 表1 客户信息表 表2 车场/车辆信息表 遗传算法参数设置如下:种群规模S=400,迭代次数T=1000,交叉概率Pc=0.5,变异概率Pm=0.03。算法通过VC++6.0编程实现,在Win7操作系统的计算机上运行。运算结果如表3所示,其中,总费用为8306元;车辆路径如图2所示,适应度随遗传迭代次数变化的进化曲线如图3所示。 表3 车辆调度方案 图2 车辆路径示意图Fig.2 Schematic diagram of vehicle path 图3 进化曲线Fig.3 Evolution curve 图2中,小圆点表示客户,大圆点表示车场,数字为客户编号,连线表示车辆的行驶路线;“A,31,3”表示A车场第1辆车起始编号为31,共有3辆车,“B,34,3”和“C,37,4”含义类推。 客户平均需求量为28,车辆的平均最大装载量为131,一个客户仅被一辆车服务,这直接限制了车辆的装载率。所以,由表3可以看出,被派出车辆的装载率已经达到了较高的水平,平均装载率为80%。由图2可以看出,每辆车的配送路径所形成的环路没有出现交叉的情况,说明解的质量较高。由图3的进化曲线可以看出,随着迭代次数的增加,种群最优个体的适应度迅速减小,种群在300代左右产生的最优个体的质量已经较高,之后进化速度减缓,进化曲线在第591代收敛,最优适应度为8 306。程序运行速度快,消耗总时间为6.515 s。 为了进一步验证多染色体遗传算法的性能,将其测试结果与传统的单染色体遗传算法和标准的粒子群算法的测试结果进行对比分析。传统的单染色体遗传算法的遗传算子参考马宇红等[15]的研究成果设计。为便于对比分析,统一设定迭代次数为1 000,种群规模(或粒子数)设计为100,统计3种算法分别运行100次解的均值和标准差,并输出其运行100次的平均进化曲线。统计结果如表4所示,平均进化曲线如图4所示。 表4 测试结果统计 图4 平均进化曲线Fig.4 Average evolution curve 由表4可以看出,多染色体遗传算法的均值和标准差都大幅度优于单染色体遗传算法和粒子群算法。由图4还可以看出,粒子群算法虽然收敛较快,但易陷入局部最优;单染色体遗传算法收敛较慢,且收敛值较大;多染色体遗传算法无论是收敛速度,还是收敛值均优于其他两种算法。另外,多染色体遗传算法的进化曲线在100代左右已经达到了粒子群算法和单染色体遗传算法的进化曲线的收敛值。所以,求解MDMTVRP时,在解的质量和搜索效率方面,多染色体遗传算法都体现出良好的性能。 多车场、多车型车辆路径问题相对于单车场、单车型车辆路径问题而言,是一种更加通用且贴近实际的车辆路径问题。本文针对多车场、多车型车辆路径问题,首先建立其变量用三角标形式表示的整数规划模型,然后在此基础上设计了个体染色体数量与总车辆数量相等的多染色体遗传算法,根据配送任务的基本单位——车辆来设计染色体,从而使多车场、多车型车辆路径问题与基本的单车场、单车型车辆路径问题有效地统一起来;染色体采用链表结构表示,相比于传统的数组结构,算法很好地避免了大量无效运算;选择过程中,对适应度采用正规化技术进行处理,确保了整个遗传过程始终保持适度的选择压力;精英选择的应用保证了种群优良基因的延续。实验结果表明,本文所设计的多染色体遗传算法不仅具有很高的搜索效率与较高的收敛速度,而且解的质量和稳定性也很高。 进一步的研究拟考虑加入“时间窗”约束,将此算法应用于带时间窗的多车场、多车型车辆路径问题,从而使研究对象更加切合实际,使算法更加具有通用性。 [1] 叶志坚, 叶怀珍, 周道平, 等. 多车型车辆路径问题的算法[J]. 公路交通科技, 2005, 22(5): 147-151. YE Zhijian, YE Huaizhen, ZHOU Daoping, et al. Heuristics for the Fleet Size and Mix Vehicle Routing Problem[J]. Journal of Highway and Transportation Research and Development, 2005, 22(5): 147-151. [2] GENDREAU M, LAPORTE G, MUSARAGANYI C. A Tabu Search Heuristic for the Heterogenous Fleet Vehicle Routing Problem[J]. Computers & Operations Research, 1999, 26(12): 1153-1173. [3] FISHER M L, TANG B X, ZHENG Z. A Network Flow Based Heuristic for Bulk Pickup and Delivery Routing[J]. Transportation Science, 1995, 29(1): 45-55. [4] GIOSA I D, TANSINI I L, VIERA I O. New Assignment Algorithms for the Multi-depot Vehicle Routing Problem[J]. Journal of the Operational Research Society, 2002, 53(9): 977-984. [5] 刘琼, 刘秀城, 张超勇, 等. 基于改进蚁群算法的带时间窗废品收集车辆路径问题[J]. 中国机械工程, 2015, 26(2): 247-254. LIU Qiong, LIU Xiucheng, ZHANG Chaoyong, et al. Waste Collection Vehicle Routing Problem with Time Windows Based on Improved Ant Colony Optimization[J]. China Mechanical Engineering, 2015, 26(2): 247-254. [6] DAN Z G, CAI L N, ZHENG L. Improved Multi-agent System for the Vehicle Routing Problem with Time Windows[J]. Tsinghua Science and Technology, 2009, 14(3): 407-412. [7] SUREKHA P, SUMATHI S. Solution to Multi-depot Vehicle Routing Problem Using Genetic Algorithms[J]. World Applied Programming, 2011, 1(3): 118-131. [8] SALHI S, WASSAN W, HAJARAT M. The Fleet Size and Mix Vehicle Routing Problem with Backhauls: Formulation and Set Partitioning-based Heuristics[J]. Transportation Research, 2013, 56: 22-35. [9] 马建华, 房勇, 袁杰. 多车场、多车型最快完成车辆路径问题的变异蚁群算法[J]. 系统工程理论与实践, 2011, 31(8): 1508-1516. MA Jianhua, FANG Yong, YUAN Jie. Mutation Ant Colony Algorithm for Multiple-depot Multiple-types Vehicle Routing Problems with Shortest Finish Time[J]. Systems Engineering Theory & Practice, 2011, 31(8): 1508-1516. [10] 罗鸿斌. 多车场、多车型车辆调度问题的改进粒子群算法[J]. 计算机工程与应用, 2014, 50(7): 251-253. LUO Hongbin. Study on Multi-depots and Multi-vehicles Vehicle Scheduling Problem Based on Improved Particle Swarm Optimization[J]. Computer Engineering and Applications, 2014, 50(7): 251-253. [11] SUNDAR K, VENKATACHALAM S, RATHINAM S. Formulations and Algorithms for the Multiple Depot, Fuel-constrained, Multiple Vehicle Routing Problem[C]// American Control Conference 2016. Boston, 2016: 10.1109/ACC. 2016. 7526691. [12] 田冉, 孙林夫, 唐慧佳, 等. 多车场物流协同运输调度问题研究[J]. 计算机工程与应用, 2015, 51(21): 230-236. TIAN Ran, SUN Linfu, TANG Huijia, et al. Research on Vehicle Logistics Transportation Scheduling Problem[J]. Computer Engineering and Applications, 2015, 51(21): 230-236. [13] CHENG R, GEN M. Evolution Program for Resource Constrained Project Scheduling Problem[J]. Evolutionary Computation, 1994, 11(3): 274-287. [14] 米凯利维茨Z. 演化程序——遗传算法和数据编码的结合[M]. 北京: 科学出版社, 2000: 24-33. MICHALEWICZ Z. Genetic Algorithms + Data Structures = Evolution Programs[M]. Beijing: Science Press, 2000: 24-33. [15] 马宇红, 姚婷婷, 张芳芳. 多车场、多车型车辆调度问题及其遗传算法[J]. 数学的实践与认识, 2014, 44(2): 107-114. MA Yuhong, YAO Tingting, ZHANG Fangfang. Multi-depot Multi-type Vehicle Scheduling Problem and Its Genetic Algorithm[J]. Mathematics in Practice and Theory, 2014, 44(2): 107-114.2.6 选择
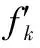
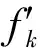
2.7 精英选择
3 算例分析
3.1 算例验证



3.2 对比分析

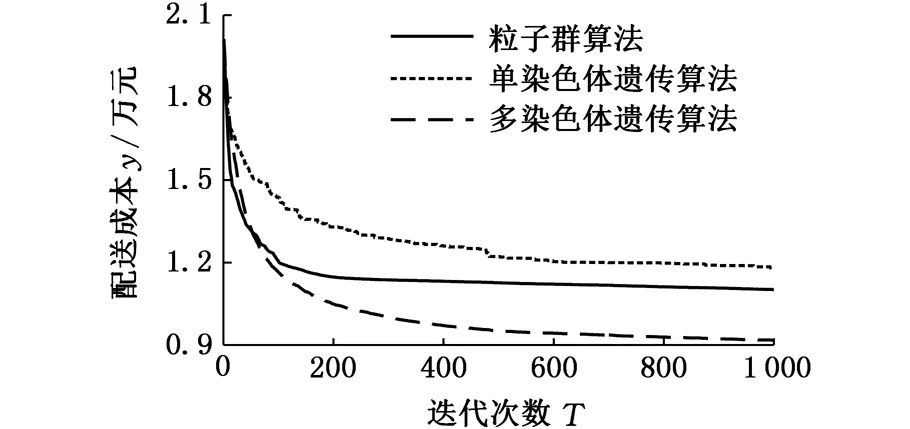
4 结语

